基于自适应模糊PID的四旋翼飞行器悬停控制

王 健，王承龙，李 智，王勇军，

（1.桂林电子科技大学信息与通信学院，广西桂林 541004；2.桂林航天工业学院无人遥测重点实验室，广西桂林 541004）

基于自适应模糊PID的四旋翼飞行器悬停控制

王 健1，王承龙1，李 智2，王勇军1，2

（1.桂林电子科技大学信息与通信学院，广西桂林 541004；2.桂林航天工业学院无人遥测重点实验室，广西桂林 541004）

为了解决四旋翼飞行器在悬停飞行过程中控制性能差、鲁棒性差等问题，提出一种基于自适应模糊PID控制方法。根据Newton-Euler方程建立四旋翼飞行器的非线性模型，设计内环为姿态控制，外环为位置控制，并在Matlab环境下设计了该自适应模糊PID控制器。仿真和实验结果表明，该自适应模糊PID控制器具有较好的响应速度及鲁棒性，能够有效地控制飞行器到达目标位置，并且保持悬停飞行状态，实现了对四旋翼飞行器系统双环控制。

四旋翼飞行器；动力学建模；自适应模糊PID控制；悬停控制

四旋翼飞行器是一种可垂直起降的飞行器，在航拍测绘、森林火灾监测、电力检修和军事侦察等方面有着广泛的应用［1］。对四旋翼飞行器的控制，会遇到如下问题：1）由于四旋翼飞行器是一种欠驱动、强耦合、多变量、非线性的复杂系统，因此难以实现对仅由4个旋翼驱动、6自由度飞行器控制；2）很难建立准确的动力学模型；3）飞行器在飞行过程中易受到空气阻力、陀螺效应、外部扰动等因素的影响［2］，且抗干扰能力弱。目前国内外研究机构针对以上问题设计的飞行器控制器，主要有线性二次型最优（LQR）控制器、经典PID控制器、反步（backstepping）控制器、神经网络控制器和滑模（sliding-mode）控制器等。经典PID控制器适用于精确的系统模型，但不能在线实时调节参数［3］；反步控制器运算量较大［4］；滑模控制器具有较好的鲁棒性，但容易导致控制飞行器抖动发生［5］。

为有效地解决飞行稳定问题，根据四旋翼飞行器非线性模型，设计了自适应模糊PID控制算法［6-8］。该控制器由姿态控制器和位置控制器组成，对飞行器实现双环模糊PID控制。通过仿真和实验验证，该控制方法结合了模糊控制算法鲁棒性好，且不依赖精确模型，相较经典PID控制算法，具有响应调节速度快的优点，能够很好地实现对四旋翼飞行器悬停控制，具有较好的控制性能。

1 四旋翼飞行器非线性数学模型描述

四旋翼飞行器是具有4个控制输入量、6自由度的欠驱动系统，在飞行过程中容易受到外部扰动的干扰，不能获得准确的气动性能参数［9］，难以建立准确有效的动力学模型。为了建立相对准确的飞行器数学模型，作如下设定：1）地理坐标系为惯性坐标系，重力加速度不随高度的变化而变化，不考虑地球自转情况；2）在研究过程中将四旋翼飞行器视为刚体系统，不考虑形变等情况；3）飞行器在飞行过程中受到的空气阻力不变。

在上述设定条件下，悬停状态下四旋翼飞行器动力学结构如图1所示。采用欧拉角表示飞行器的姿态，欧拉角表示为Φ＝［φ，θ，φ］T。定义图1所示的2个坐标系，即惯性坐标系E＝｛XeYeZe｝和机体坐标系B＝｛XbYbZb｝。从机体坐标系B到惯性坐标，系E的坐标变换矩阵［10］为：

图1 四旋翼飞行器动力学示意图Fig.1 Dynamic structure of four-rotor aircraft

其中：φ为绕Xb轴旋转的滚转角；θ为绕Yb轴旋转的俯仰角；ψ为绕Zb轴旋转的偏航角。根据Newton-Euler定理对悬停状态下四旋翼飞行器进行受力分析可知，飞行器的动力学模型为：

其中：m为无人飞行器质量；为无人飞行器重心位置的加速度；Ft＝（Fx，Fy，Fz）T为飞行器的总升力；为单个旋翼的升力，kt为升力系数，ωi为旋翼转速；为飞行器所受阻力，kdt为阻力系数矩阵；Fm＝［0，0，mg］T为飞行器的重力。则四旋翼飞行器所受的升力为：

由式（1）～（3）可得线性加速度方程：

其中：kdt，x、kdt，y、kdt，z为kdt在机体坐标系X、Y、Z轴的分量。根据前面假设飞行器的结构和质量是对称的，可定义I＝diag（Ix，Iy，Iz）为飞行器的转动惯量矩阵，作用在机体上的力矩矩阵为M＝diag（Mx，My，Mz），Ω＝［p，q，r］T为飞行器角速度，则有

根据欧拉定理可知，欧拉角［φ，θ，φ］T与机体坐标系下角速度［p，q，r］T的旋转矩阵为：

由式（5）、（6）可得姿态角加速度：

将飞行器4个旋翼转速作为输入变量，定义四旋翼飞行器的被控制对象输入量为u＝［u1u2u3u4］T，其中：u1为垂直速度控制量；u2为滚转输入控制输入量；u3为俯仰输入控制输入量；u4为偏航输入控制输入量。则控制输入量为：

综上可得，悬停状态下四旋翼飞行器非线性系统模型为：

2 自适应模糊PID控制器设计

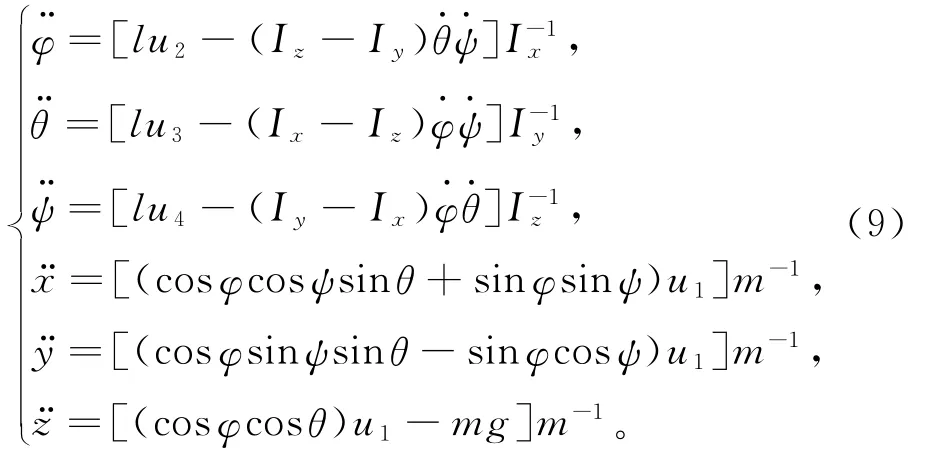
由所建立的数学模型可知，四旋翼飞行器是多输入多输出的非线性系统。为了使飞行器具有较好的控制性能并最终实现稳定悬停，采用自适应模糊PID控制器对四旋翼飞行器进行控制。根据上述所建模型，把分环控制的控制系统分为2个部分，其中，内环为姿态控制，外环为位置控制。四旋翼飞行器控制框图如图2所示。

图2 四旋翼飞行器控制框图Fig.2 Block diagram of four-rotor aircraft control

当飞行器控制系统接收到目标位置命令后，位置控制回路计算系统所要改变的目标姿态角，然后输入至姿态控制回路，控制其响应的姿态角。到达目标位置后，通过位置反馈确定水平位置和垂直高度，通过姿态反馈完成姿态稳定，实现位置控制和姿态控制，最终实现对四旋翼飞行器稳定悬停控制。

2.1 姿态控制

飞行器姿态稳定是飞行器稳定飞行的基础，要实现对飞行器姿态角的实时精确控制，首先需要采用飞行器的航姿传感器实时采集飞行器在3个轴向的角度和角速度，然后采用自适应模糊PID控制器对姿态角进行控制，通过不断地调节姿态角，最终实现悬停状态下姿态角稳定控制。定义目标姿态角为［φd，θd，ψd］，航姿传感器采集的姿态角信息为 ［φ，θ，ψ］。利用控制器对设定的目标姿态角与采集的姿态角的偏差进行调节。以控制飞行器的滚转姿态角φ为例，根据建立姿态角模型可知横滚角加速度为，则滚转姿态角控制为：

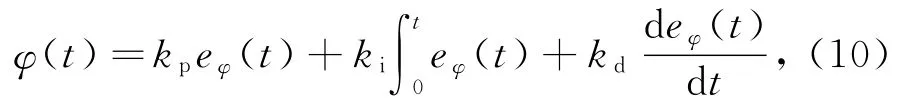
其中：φ（t）为滚转角控制量；eφ（t）为滚转角误差eφ（t）＝φd（t）-φ（t）；kp为比例系数；ki为积分系数；kd为微分系数。对控制函数进行拉普拉斯变换：

姿态角控制器框图如图3所示，在PID控制器的基础上加入模糊控制，以姿态角误差e及其变化率ec作为模糊控制器的输入，kp、ki、kd为模糊控制器输出。其中，根据设定的模糊规则将姿态角误差e及其变化率ec表示为对应的模糊量E、EC。E、EC的基本论域为［-6，＋6］，将其离散为13个等级即为｛-6，-5，-4，-3，-2，-1，0，＋1，＋2，＋3，＋4，＋5，＋6｝，同时考虑控制精度的要求，将论域划分为负大［BN］、负中［NM］、负小［NS］、零［ZO］、正小［PS］、正中［PM］、正大［PB］等7个语言变量，然后由e、ec隶属函数根据最大值法得出相应的模糊变量［11］。自适应模糊PID控制器通过不断检测姿态角误差及其变化率，同时根据所设定的模糊规则产生相应的输出，在PID控制器初始参数的基础上进行实时动态调节。同理，根据所涉及的控制器，可实现对俯仰角和偏航角的稳定控制。

图3 姿态角控制框图Fig.3 Block diagram of attitude control

2.2 位置控制

位置控制分为水平方向和垂直方向的位置控制，其中垂直方向位置控制为高度控制，利用气压计测得的实际高度z与期望高度zd的差值作为控制量，可知高度控制为：

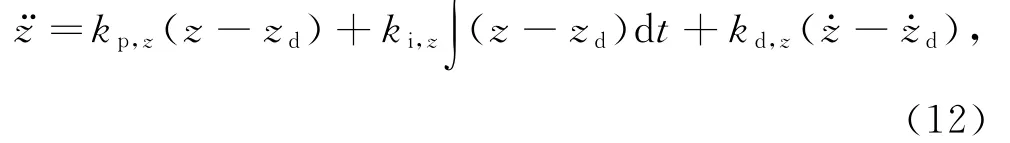
其中：为目标高度加速度参量，所建高度模型为，高度控制量u1为：

对水平方向位置控制，首先设（xd，yd）为水平方向期望目标位置，将其与飞行位置进行对比得到位置误差，将位置误差作为输入量，根据所建位置模型，则水平位置控制为：

、作为水平方向的加速度参量。由加速度参量可计算得到目标滚转角φd和目标俯仰角θd分别为：

φd和θd作为姿态控制器的输入信号，同时分别将姿态和位置信号反馈到输入端构成闭环反馈系统，实现四旋翼飞行器姿态和位置的双环控制。在PID控制的基础上加入模糊控制，以位置误差量及其变化率作为模糊控制输入，通过实时采集的高度位置信息与期望位置进行对比，实时调节kp、ki、kd的参数。

2.3 自适应模糊控制参数调节规则

采用自适应模糊PID对四旋翼飞行器姿态和位置控制，为使该控制器具有较好的控制响应速度，同时具有较好的鲁棒性，根据PID控制参数对系统动态控制和稳态控制影响设定对应的调节规则。以参数kp调节为例，根据姿态和位置的误差及其变化率的大小，kp的取值影响系统控制的响应速度，若kp取值过大，能够提高控制器的响应速度，减小稳态误差，但同时也会带来一定的超调量；若kp取值过小，控制器响应速度会很慢，调节时间变长。因此，对kp调节，在调节初期应当适当取较大的值以提高响应速度；在调节中期，kp取较小值，减小系统的超调量；在调节后期，适当增大kp的值以减小稳态误差，提高控制稳定性。同理，ki、kp控制参数调节也需要根据控制器输入的姿态和位置的误差及其变化率的大小，在线实时调节其大小，实现对飞行器快速控制并具有较好的稳定性，最终实现四旋翼飞行器稳定悬停飞行。根据建立的非线性四旋翼模型，设计相应的模糊控制规则如表1所示。

表1 模糊控制规则Tab.1 Rule of fuzzy control

3 实验结果及分析

在Matlab环境下对悬停状态下四旋翼飞行器进行控制仿真，将上述自适应模糊PID控制器用于四旋翼飞行器，仿真模型参数如表2所示。

3.1 姿态控制结果分析

依据上述模型参数，设置悬停状态下四旋翼飞行器的初始姿态角为［0，0，-1°］，目标姿态角为［0，0，0］，采用自适应模糊PID进行姿态控制，姿态角响应曲线如图4所示。

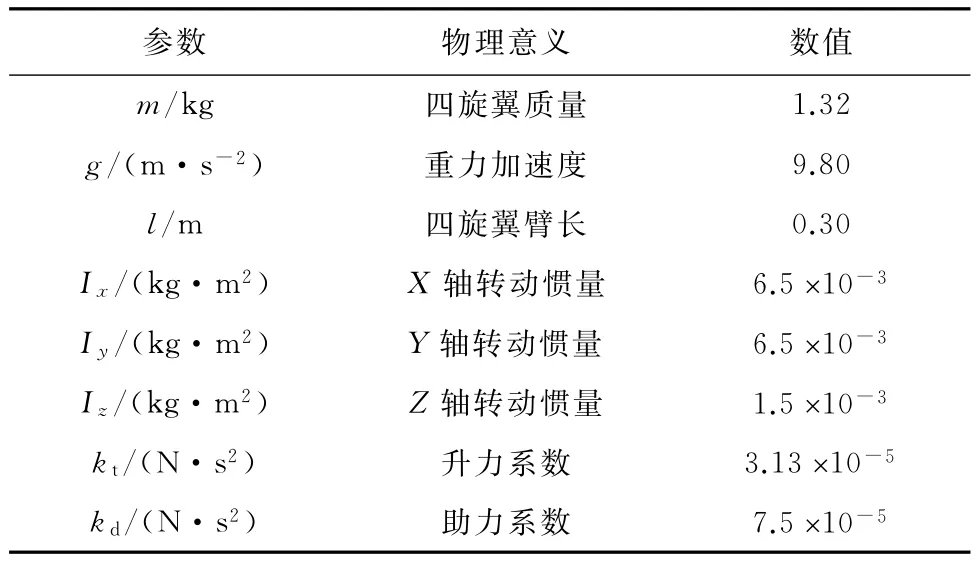
表2 飞行器模型参数Tab.2 Parameters of four-rotor aircraft

图4 飞行器姿态角响应曲线Fig.4 Attitude simulation of four-rotor aircraft

由图4可知，自适应模糊PID控制器可将飞行器的姿态角误差控制在±0.5°左右，控制精度较高，同时在6～8s内能稳定在目标姿态，具有较好的响应速度，超调量小。

3.2 位置控制结果分析

设定四旋翼飞行器的初始位置为［20，-10，0］，悬停状态下目标位置为［0，0，30］。采用自适应PID模糊进行位置控制，其中位置响应曲线如图5、6所示。

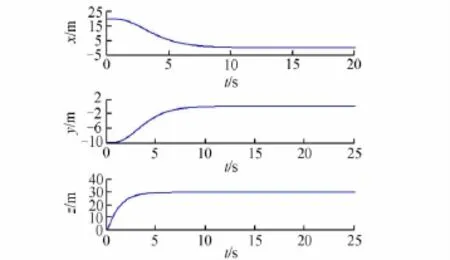
图5 飞行器位置响应曲线Fig.5 Position simulation of four-rotor aircraft

图6 飞行器悬停响应曲线Fig.6 Hovering control simulation of four-rotor aircraft

从图5、图6可看出，自适应模糊PID控制器可在6～8s内使飞行器悬停到目标位置，具有较好的响应速度，并且能够稳定悬停在［0，0，30］处，实现稳定悬停飞行。其能较快地响应，具有较好的鲁棒性，且超调量小，具有较好的抗干扰能力。

3.3 实际悬停飞行控制结果

本设计搭建了以STM32F405RGT6为主控制器的飞行器物理测试平台，该飞行器控制系统通过MPU6050传感器实时采集姿态角数据，使用GPS与气压计实时采集在实际飞行过程中的位置数据。实际飞行测试如图7所示，经过多次实际飞行实验，验证了所设计的自适应模糊PID控制器能够实现四旋翼飞行器快速、稳定悬停飞行。

图7 悬停飞行控制测试Fig.7 Test of hovering flight control

4 结束语

针对四旋翼飞行器悬停控制，设计了自适应模糊PID控制算法，将飞行器控制系统分为位置控制和姿态控制2个子系统，利用该控制器对飞行器进行内环姿态控制和外环位置控制，实现飞行器稳定悬停飞行。仿真实验结果表明，自适应模糊PID控制器能实现对飞行器稳定悬停飞行的控制，实际飞行结果验证了自适应模糊PID控制方法的有效性。

［1］ 聂博文，马宏旭，王剑.微小型四旋翼飞行器的研究现状与关键技术［J］.电光与控制，2007，4（3）：34-40.

［2］ BOUABDALLAH S.Design and control of quadrotors with applications to autonomous flying［J］.Ecole Poly Technique Federalede Lausanne，2007（2）：1-15.

［3］ NICOM P，MANUKID P.Attitude and altitude control of a four-rotor hovercraft using sliding mode control with adaptive sliding surface［C］／／IEEE international Conference on Robotics and Biomimetics，2011：1285-1290.

［4］ FARAHNAZ J，AHMAD F.Fuzzy integral backstepping control approach in attitude stabilization of a quadrotor UAV［C］／／Iranian Conference on Fuzzy Sys-tems，2013：1-6.

［5］ BORA E，ERDINC A.Modeling and PD control of a quadrotor VTOL vehicle［C］／／IEEE Intelligent Vehicles Symposium Istanbul，2007：691-699.

［6］ EHASAN A，MOHAMMAD A.Attitude Control using an extended calssifier system algorithm for offline autotuning of a PID controller［C］／／IEEE RSI／ISM International Conference on Robotics and Mechatronics，2014：930-935.

［7］ 李俊，李运堂.四旋翼飞行器的动力学建模及PID控制［J］.辽宁工程技术大学学报（自然科学版），2012（2）：1-4.

［8］ 李一波，宋述锡.基于模糊自整定PID四旋翼无人机悬停控制［J］.控制工程，2013（5）：10-14.

［9］ 张镭，李浩.四旋翼飞行器模糊PID姿态控制［J］.计算机仿真，2014，32（1）：28-31.

［10］ 林旭梅，王婵.四旋翼飞行器的自适应鲁棒滑膜控制器设计［J］.仪器仪表学报，2015（7）：7-14.

编辑：梁王欢

Hovering control of four-rotor aircraft based on adaptive fuzzy proportion integration differentiation

WANG Jian1，WANG Chenglong1，LI Zhi2，WANG YongJun1，2
（1.School of Information and Communication Engineering，Guilin University of Electronic Technology，Guilin 541004，China；2.Key Laboratory of Unmanned Aerial Vehicle Telemetry，Guilin University of Aerospace Technology，Guilin 541004，China）

In order to improve control performance，robustness of the four-rotor aircraft in the process of hovering flight，a control method based on fuzzy adaptive proportion integration differentiation is proposed.Firstly Newton-Euler equations are used to construct the non-linear model of four-rotor aircraft.Then the inner loop of attitude control is designed，the outer loop of position control is designed，and the adaptive fuzzy PID controller is designed by Matlab.Finally simulation results show that the adaptive Fuzzy PID controller has better response speed and robustness，it can effectively make the aircraft reach the target position and remain hovering flight.The bicyclic control of four-rotor aircraft is realized.

four-rotor aircraft；dynamic modeling；adaptive fuzzy PID；hovering control

V249.1；TP273.4

：A

：1673-808X（2016）05-0406-06

2016-01-26

国家自然科学基金（61361006）；广西自然科学基金（2015GXNSFBA139251）；桂林航天工业学院院级基金（YJ1304）

王健（1973-），女，新疆乌鲁木齐人，副教授，研究方向为智能信号处理。E-mail：wangjian＠guet.edu.cn

王健，王承龙，李智，等.基于自适应模糊PID的四旋翼飞行器悬停控制［J］.桂林电子科技大学学报，2016，36（5）：406-411.