基于城市权重的蚁群算法及其在TSP中的应用*

2017-01-16马清鑫张达敏阿明翰

通信技术 2016年11期

关键词：蚁群蚂蚁权重

马清鑫，张达敏，张斌，阿明翰

（贵州大学大数据与信息工程学院，贵州贵阳550025）

基于城市权重的蚁群算法及其在TSP中的应用*

马清鑫，张达敏，张斌，阿明翰

（贵州大学大数据与信息工程学院，贵州贵阳550025）

蚁群算法在解决NP-C问题时展现出了较强的适用性，但收敛速度慢，容易陷入局部最优解的缺陷却没有得到较好解决。于是，提出了一种基于城市权重的蚁群算法ACAWC（Ant Colony Algorithm based on the W eight of City）。改进后的算法通过利用城市距离在整个城市网中所占比重来协调启发信息作用，同时应用双重赌盘算法和双重随机性的思想，增强了跳出局部最优解的概率，并改进了依据路径贡献度的信息素更新机制，加快了算法的收敛速度。仿真实验表明，ACAWC算法求得的最优解比基本蚁群算法提高了10%～15%，同时也一定程度地提高了收敛速度。

城市权重；蚁群算法；TSP；信息素

0 引言

TSP（Traveling Salesman Problem）问题又称旅行商问题或最短路径问题。通常可以描述为：已知N个城市及相互间的距离，旅行商从某城市出发访问各城市且仅访问一次后再回到原点的一条最短巡回路径。作为典型的NP-C问题，旅行商问题已被广泛应用于车间作业调度﹑网络路由布设等方面。为了有效解决TSP问题，许多启发式搜索算法被用来解决这一问题，如遗传算法（GA）﹑蚁群算法（ACA）﹑模拟退火算法（SAA）﹑人工免疫算法（AIA）等[1]。其中，因蚁群算法类似一个增强型学习系统，具有正反馈﹑分布式﹑并行式﹑自组织等优点，使得在解决NPC问题时具有独特的优势。然而，信息素反馈机制有其明显的缺陷。信息素反馈机制过强，会使算法出现停滞甚至陷入局部最优解；相反，要找出最佳路径则需要较长的时间[2]。

Dorigo M等[3]提出利用自适应蚁群算法调控信道资源配置，降低通信过程中的负担，以达到系统能耗最优化；丁建立等[4]提出了将蚁群和遗传算法结合的融合算法，基于遗传算法调控信息素分布，再应用蚁群寻优解决路径优化问题，较好地解决了TSP求解精度的问题；黄国锐等[5]提出一种基于信息素扩散的蚁群算法（PDACO），通过信息素扩散机制，使相邻或近距离的蚂蚁更加协调地工作；田富鹏[6]提出了一种改进的蚁群算法，引入信息素挥发系数的自适应控制策略以及将信息素浓度控制在[min-max]中，有效避免了蚁群算法陷入停滞的状态；袁东辉等[7]通过优化信息素蒸发机制，并引入贪婪策略来改进蚁群算法，并将改进的蚁群算法应用于网络节点部署，取得了较好的效果。

为了有效改善蚁群算法存在的缺陷，本文在借鉴前人研究蚁群算法和TSP问题的基础上，提出了基于城市权值的信息素初始化矩阵，有效改善了蚁群因前期信息素缺乏而过度依赖启发信息，减少了算法搜索时间；利用状态转移概率寻找下一个节点时，采用了双重轮盘算法，有效增加了可行解的搜索范围，并改进了自适应蚁群信息素更新机制，避免信息素淹没启发因子，帮助算法跳出局部最优解，进而找到全局最佳路径。

1 基本蚁群算法

在觅食过程中，单只蚂蚁的行为比较简单，然而蚁群却能够表现出及其复杂的行为。通过研究发现，蚂蚁在寻找食物的过程中，会留下一种叫做信息素的物质。所有的蚂蚁均能感知这种物质，并通过信息素的量来选择前进的方向。这种信息素具有叠加和挥发的双重特性，于是大量蚂蚁组成的蚁群集体行为就表现出一种信息正反馈现象，即某路径上走过的蚂蚁越多，则后来者选择该路径的概率就越大。经过一段时间便会形成一条高浓度信息素路径，该路径便是蚂蚁搜索到的寻找食物的最短路径。受此启发，Dorigo M于1991年提出了蚁群算法。

基本蚁群算法求解TSP的步骤如下。

（1）信息素初始化

信息素初始化：

其中τij(0)表示初始时刻城市i与城市j之间的信息素浓度；const为常数，一般取值为0。

（2）状态转移

状态转移：

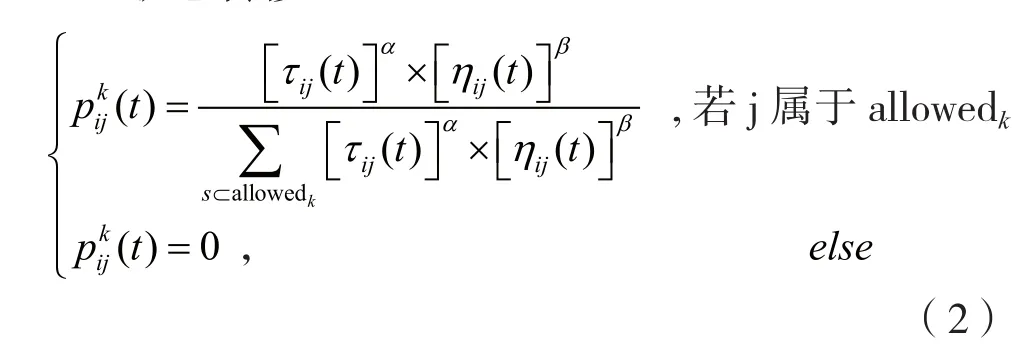
（3）信息素的更新

蚁群在转移过程中，要对残留信息进行更新处理。同时，考虑到信息素的挥发，t+n时刻路径(i, j)上的信息量可按以下规则进行调整：

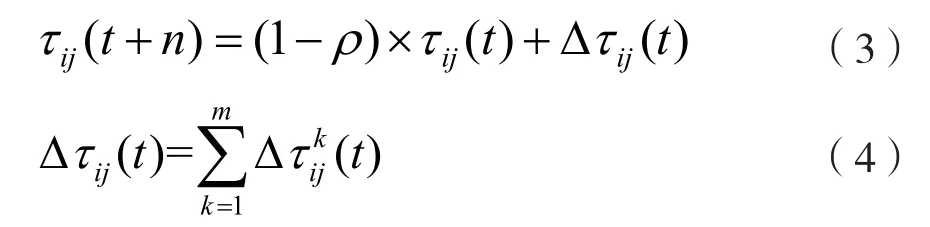
其中，ρ表示信息素挥发系数，其取值范围为ρ⊂ ［0,1］；Δτij(t)表示本次循环中路径(i, j)上的信息素增量。

Dorigo M根据信息素更新策略的不同，提出了三种信息素更新模型，分别称之为Ant-Cycle模型﹑Ant-Quantity模型及Ant-Density模型。考虑到更新信息素浓度的全局性，通常使用Ant-Cycle模型：

其中，Q表示信息素强度，Lk表示第k只蚂蚁在本次循环中所走路径的总长度。

2 基于城市权重的蚁群算法

针对蚁群算法存在收敛时间长，易陷入局部最优解的问题，本文提出了基于城市权重的蚁群算法（ACAWC）。该算法主要实现策略包括初始信息素浓度分布﹑状态转移概率更新﹑信息素更新机制调整三部分。

2.1 初始信息素浓度分布

基本蚁群算法中，初始的信息素矩阵为常矩阵，则转移概率只依赖于城市间距离，会导致蚂蚁从开始就放弃最优路径上的较长距离。为了解决这一问题，吴华锋等[9]提出基于城市间的距离与城市规模之商作为初始信息素分布矩阵：

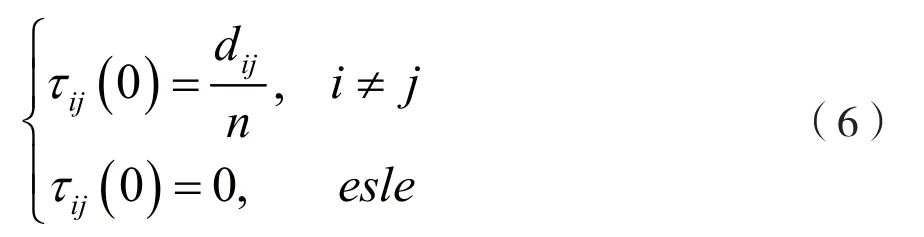
但该思想存在较为明显的缺陷。初始信息素浓度与启发信息成反比，虽然在一定程度上削弱了启发信息的作用，使选择最优路径上较长路径的概率增加，但并不是每一条较长路径都在最佳路径上，相反，绝大多数较长路径都不在最佳路径上。因此，寻找平衡时间和空间的初始信息素浓度矩阵尤为重要。

针对这种缺陷，在算法初期首先计算每个城市在城市网中的权重，即每个城市到其他各个城市距离之和与城市规模之商，再根据两城市权重的平均值初始化信息素，利用全局信息量，可有效降低放弃最优路径上较长距离的同时，减少蚁群的搜索时间。因此，改进后的蚁群算法，信息素初始分布矩阵为：

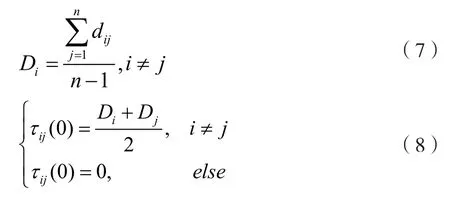
2.2 状态转移概率更新机制

基本蚁群算法及其之后的改进只是把两城市距离的倒数作为期望因子，即ηij(t)=1/dij。选择下一个城市时，只看到目前两城市之间距离，而忽略了下一个城市与其他城市的关系。基于上文提出的城市权重思想，提出了基于城市权重的期望启发信息：

改进后蚁群算法的状态转移概率计算公式仍然依据基本蚁群算法，即：

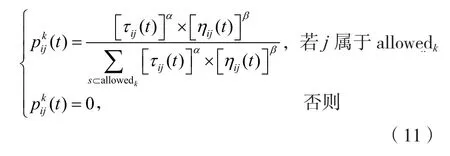
通常，蚂蚁k在选择下一个要遍历的城市时，通常采用赌盘算法[8]，即依据概率并结合随机特性来选择下一个城市。本文引入双重赌盘算法，首先根据赌盘算法产生一系列解，这些解就是在选择下一个城市时概率比较大的城市的一个集合F；然后，再次利用赌盘算法在集合F中寻找下一个城市。这样就大大降低了算法陷入局部最优解的概率。

2.3 信息素更新机制调整

在基本蚁群算法中，信息素浓度的大小将直接影响寻找下一节点的转移概率。随着迭代的进行，信息素将逐渐集中到较少边上，导致搜索过程总是在这几条边上进行，进而求得相似解而陷入局部最优。吴华锋等[9]引入了路径贡献度（CDSP）的概念，通过对最优路径上较长路径进行信息素二次强化，增大较长路径被选择的概率，在一定程度上解决了局部最优解的情况。

本文通过引入自适应信息素挥发系数，从而随着迭代次数的增加，信息素挥发系数逐渐增大，避免期望信息被信息素淹没，同时降低蚂蚁对信息素的依赖。但是，同时为了防止信息素流失过快，不妨对信息素挥发系数设置最大值（假设为0.2，依仿真实验数据而定）：

同时，不妨借鉴上文中提到的路径贡献度（CDSP）的概念，更新公式如下：

rand是对路径贡献度大的路径的信息素浓度随机加强，q0则是路径贡献度阈值。

具体算法流程如下：

（1）参数初始化。蚁群算法中主要参数有α、β和蚂蚁的数目m等。α的大小表明每个路径上的信息量的受重视程度；β的大小代表了启发式因子的受重视程度。蚂蚁数目越多，算法的全局搜索能力越强；相反，则算法的收敛速度将减慢。

（2）将m只蚂蚁随机放在n个城市上，根据双重赌盘算法选取下一个城市。

（3）修改禁忌表。

（4）重复（2）和（3），直到所有蚂蚁走遍所有城市。

（5）判断是否满足迭代结束条件Nc≥Nmax，满足则结束循环并输出结果；若不满足，更新信息素，并清空禁忌表，进行下一次循环。

3 仿真实验与分析

为了验证ACAWC算法的收敛性和可靠性，本文将从TSPLIB中选取14个使用欧式距离的TSP实例进行测试[10-11]，每个实例运行5次。仿真实验在CPU为Intel(R) Core(TM)型号为i5-4590@3.30 GHz环境下使用MATLAB 2010b进行编程测试；算法使用各个参数由经验和试算得来，初始值设置如表1所示，仿真结果依次如图1﹑图2所示。。

表1 算法的参数设置

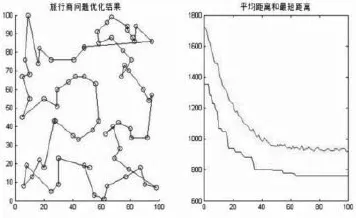
图1 基本蚁群算法求解st70最优路径

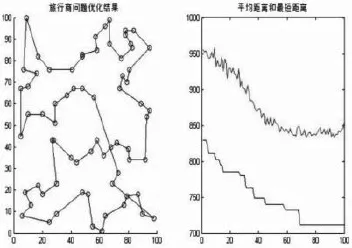
图2 ACAWC算法求解st70最优路径

对比图1﹑图2发现，在求解st70问题时，ACAWC算法在蚁群迭代到20次左右时，最优路径就已经低于800，而基本蚁群算法直到60次左右才达到上述效果。可见，ACAWC算法与基本蚁群算法相比，效率至少提高了一倍。为了说明ACAWC算法效率的普遍性，另外附上求解eil76和rat99时两种算法的对比图，如图3﹑图4﹑图5和图6所示。在效率明显提高的同时，又对比几种算法在寻找最优解方面的能力，具体如表2所示。

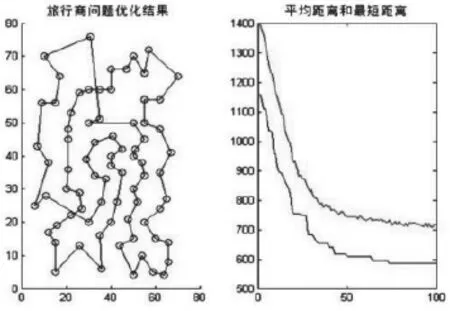
图3 基本蚁群算法求解eil76最优路径

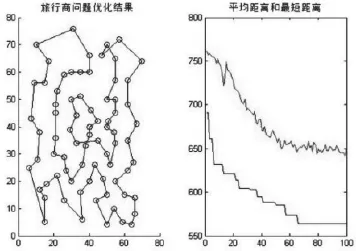
图4 ACAWC算法求解eil76最优路径

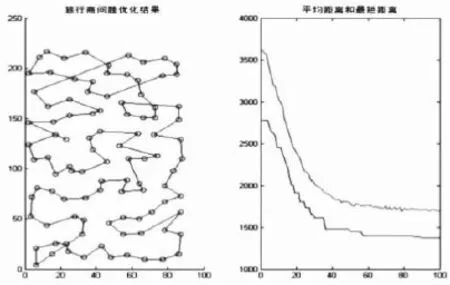
图5 基本蚁群算法求解rat99最优路径

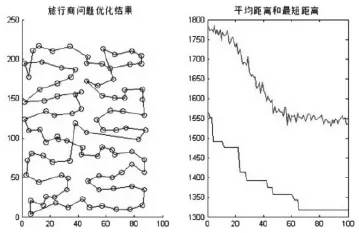
图6 ACAWC求解rat99最优路径

为了更加形象地说明仿真达到的效果，挑选路径长度在400～1 500之间的5个城市节点库来对比基本蚁群算法最优解﹑文献[8]改进蚁群算法最优解﹑本文改进蚁群算法最优解和国际最优解，结果如图7所示。

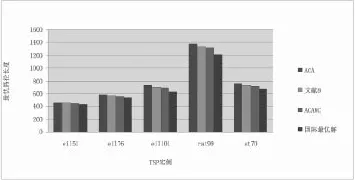
图7 三种算法与国际最优解路径长度对比

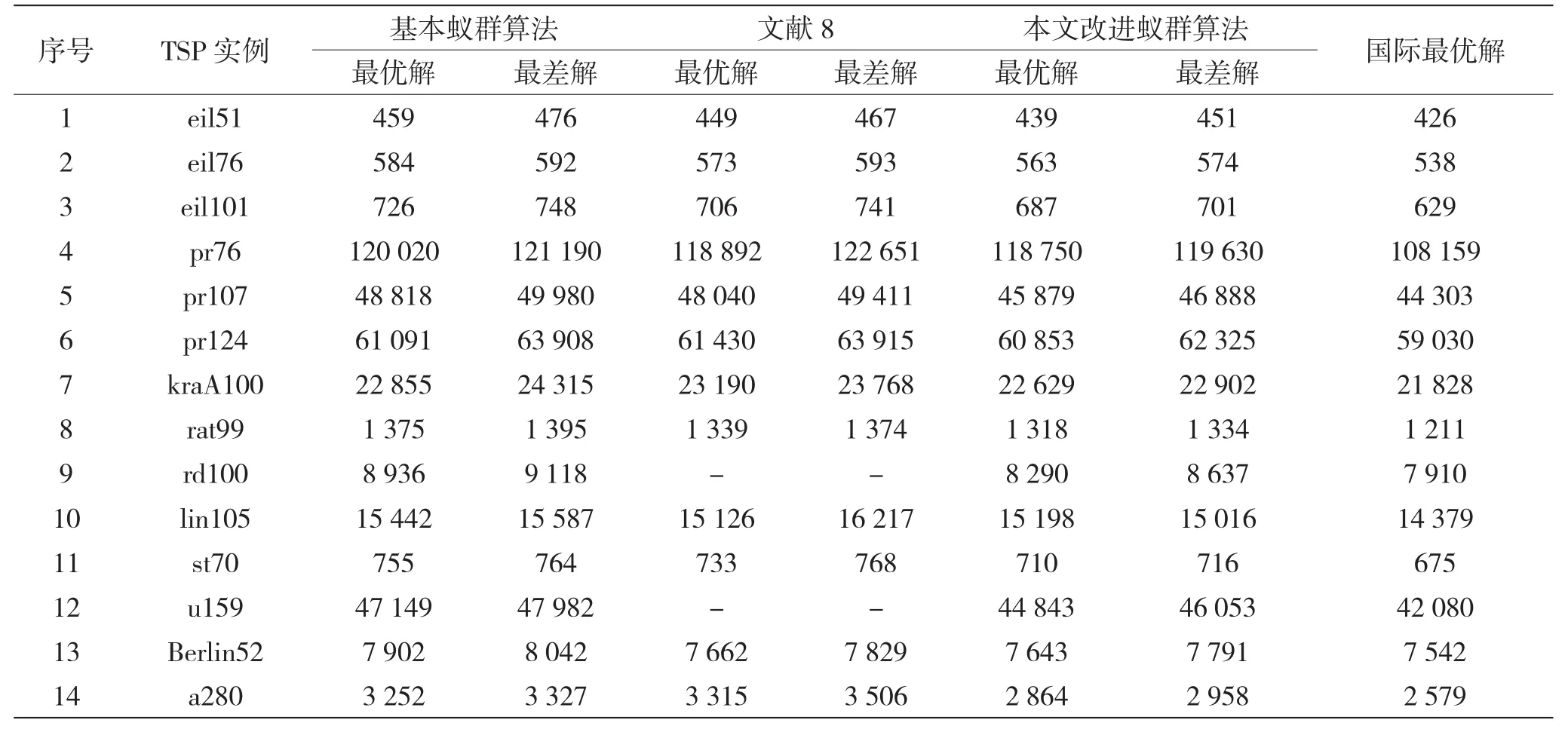
表2 基本蚁群算法与改进后蚁群算法路径长度对比

4 结语

本文提出了基于城市权重的蚁群算法(ACAWC)，并应用该算法来解决TSP问题。从仿真结果可以看出，改进的蚁群算法求得的最优解比基本蚁群算法提高了10%～15%，比文献[8]改进的蚁群算法提高了6%～8%，同时优化效率提高了将近一倍。然而，由于具体城市不确定性及参数选择存在差异以及迭代次数的限制，ACAWC算法优化解与国际最优解还存在差距，但在可接受范围之内。本文在状态转移概率机制选择上，采用了双重赌盘算法，虽然最优解得到了很大程度改善，但是双重赌盘算法需要进行两次状态转移概率的计算，这无疑会造成优化效率的下降。随着城市节点的增多，这种效率下降尤为明显。因此，未来如何更好地权衡效率与最优解，将成为研究的重点。同时，如何将上述思想应用于解决大规模TSP问题以及更多组合优化问题将成为研究的方向。

[1] 朱献文,李福荣.求解旅行商问题的几种智能算法[J].计算机与数字工程,2010,32(01):32-35.

ZHU Xian-wen,LI Fu-rong.Several Intelligent Algorithms for Solving Traveling Salesman Problem[J].Computer& Digital Engineering,2010,32(01):32-35.

[2] COLORINI A,DORIGO M,MANIEZZO V,et al.Distributed optimization by ant colonies[C].Proceedings of the 1st European Conference on Artificial Life,1991:134-142.

[3] DORIGO M,MANIEZZO V,COLORINI A,et al.Ant System: Optimization by a Colony of Cooperating Agents[J].IEEE Transactions on Systems Man and Cybernetics-Part B,1996,26(01):29-41.

[4] 丁建立,陈增强,袁著祉.遗传算法与蚂蚁算法的融合 [J].计算机研究与发展,2003,40(09):1351-1356.

DING Jian-li,CHEN Zeng-qiang,YUAN Zhu-zhi.The Combination of Genetic AlgorithMand Ant Algorithm[J]. Journal of Computer Research and Development, 2003,40(09):1351-1356.

[5] 黄国锐,曹先彬,王煦法.基于信息素扩散的蚁群算法[J].电子学报,2004,32(04):865-868.

HUANG Guo-rui,CAO Xian-bin,WANG Xu-fa.Ant Colony Algorithm based on Pheromone Diffusion[J]. ACTA ELECTRONICA SINISC,2004,32(04):865-868.

[6] 田富鹏.改进型蚁群算法及其在TSP中的应用[J].兰州大学学报:自然科学版,2005,41(02):78-80.

TIAN Fu-peng.An Improved Model of Ant Colony AlgorithMand Its App lication in TSP[J].Journal of Lanzhou University(Natural Science),2005,41(02):78-80.

[7] 袁东辉,刘大有,申世群.基于蚁群—遗传算法的改进多目标数据关联方法[J].通信学报,2011,32(06):17-23.

YUAN Dong-hui,LIU Da-you,SHEN Shi-qun.An Improved multi objective data association method based on ant colony and genetic algorithm [J].JOURNAL OF CHINA INSTITUTE OF COMMUNICATIONS, 2011,32(06):17-23.

[8] 姜坤霖,李美安,张宏伟.面向旅行商问题的蚁群算法改进[J].计算机应用,2015,35(S2):114-117.

JIANG Kun-lin,LI Mei-an,ZHANG Hong-wei.Improved Ant Colony Algorithm for Travelling Salesman Problem[J]. Journal of Computer Applications,2015,35(S2):114-117.

[9] 吴华锋,陈信强,毛奇凰等.基于自然选择策略的蚁群算法求解TSP问题[J].通信学报,2013,34(04):165-170.

WU Hua-feng,CHEN Xin-qiang,MAO Qi-huang,et al.Improved Ant Colony Algorithm based on Natural Selection Strategy for Solving TSP Problem [J].Journal on Communications,2013,34(04):165-170.

[10] TSPLIB[EB/OL].http://www.iwr.uni-heidelberg.de/groups/ comopt/software/TSPLIB95/.

[11] WANG L,ZHU Q.An Efficient Approach for Solving TSP:the Rapidly Convergent Ant Colony Algorithm[C]. Fou rth In ternational Con ference on Natu ral Computation,2010:448-452.

Ant Colony A lgorithm based on W eight of City and Its App lication in TSP

MA Qing-xin, ZHANG Da-min, ZHANG Bin, A Ming-han

(College of Data and Information Engineering, Guizhou University, Guiyang Guizhou 550025, China)

Ant colony algorithm usually exhibits strong applicability in solving NP complete problems, but easily falls into the defect of local optical solution for its fairly slow convergence rate. An ant colony algorithm based on the weight of city (ACAWC) is thus proposed. The modified algorithm, by using the proportion of urban distance in the whole city network, coordinates and arouses the information role, and again with double roulette algorithMand double randomness idea, enhances the probability of jumping out from the local optimal solution. By modifying the pheromone update mechanism based on path contribution, the algorithm is improved in its convergence speed. The simulation experiments indicate that the optimal solution froMaCAWC algorithm could acquire an improvement of 10%～15% as compared with the basic ant colony algorithm, and in addition, its convergence speed is also improved to a certain extent.

weight of city; ant colony algorithm; TSP; pheromone