基于黏弹性边界的地震动输入方法和边界条件选择研究

孙纬宇， 欧尔峰， 严松宏

(1. 兰州交通大学甘肃省道路桥梁与地下工程重点实验室，甘肃 兰州 730070；2.兰州交通大学土木工程学院，甘肃 兰州 730070； 3.甘肃省轨道交通力学应用工程实验室，甘肃 兰州 730070)

基于黏弹性边界的地震动输入方法和边界条件选择研究

孙纬宇1,2， 欧尔峰1,2， 严松宏1,3

(1. 兰州交通大学甘肃省道路桥梁与地下工程重点实验室，甘肃 兰州 730070；2.兰州交通大学土木工程学院，甘肃 兰州 730070； 3.甘肃省轨道交通力学应用工程实验室，甘肃 兰州 730070)

针对地下工程抗震分析中边界条件和地震动输入方式选择问题，对一地下半无限体模型在一剪切波垂直入射条件下进行不同边界条件和不同地震动输入方法的算例试算。结果发现：两侧采用竖直向位移约束、底部采用黏弹性边界、并在模型底部用等效节点力输入地震动的方法，与三边均采用黏弹性边界条件和三边均采用等效节点荷载输入地震动的方法可以获得同样的结果。该方法易于在ANSYS中通过APDL编程实现，可为地下工程抗震分析中黏弹性边界的使用提供便利。

地下工程； 黏弹性边界； 地震动输入； 边界条件； ANSYS

0 引言

近年来，由于地震灾害频发，地下工程的抗震问题越来越受人们的重视。而在地下工程抗震分析中，由于结构及岩土体介质动力反应的复杂性，数值方法成为目前地下结构动力研究的主要手段[1]。目前地下结构抗震分析常用的数值方法主要有：以求解波动方程为基础的波动法和以求解结构运动方程为基础的振动法。不管采用何种方法，边界条件和地震动输入方式的选择将直接影响到地下结构抗震分析的准确性和可靠性。因此诸多学者开展了边界条件和地震动输入方法的研究。Lysmer J.等[2]提出的黏性人工边界能够较好地模拟半无限空间的辐射阻尼，但不能模拟其弹性恢复能力。Deeks A.J.等[3]提出的黏弹性边界条件很好地模拟了半无限辐射阻尼和弹性恢复能力。刘晶波等[4-6]研究并发展了黏弹性边界，并将其在通用有限元软件上进行实现。从此，黏弹性边界条件得到了广泛使用。单华廷等[7]基于黏弹性边界条件进行了地下结构地震反应分析中材料非线性的影响分析；李鹏等[8]基于黏弹性边界条件进行了饱和地基中地下结构地震反应若干问题的研究；高峰等[9]进行了地下结构波动法与振动法的对比研究，推荐采用两边黏弹性边界、底边固定边界的震动法计算方法。汪精和等[10]进行了地下结构抗震分析中地震动输入方法的比较研究，推荐采用与黏弹性边界条件相匹配的等效节点力地震动输入方法。

鉴于地下结构抗震分析中采用文献[9]方法计算精度上存在的缺陷和文献[10]方法在ANSYS上进行APDL编程实现时的复杂性，本文基于黏弹性边界条件，对某一算例在多种边界条件和多种地震动输入方式下的动力响应进行试算，经过对比分析，得出一种易于APDL编程实现且精度较高的边界条件形式和地震动输入方法，可为地下工程抗震计算提供便利。

1 计算方法及原理

1.1 波动输入方法

波动法是依据波动场，将输入波动转化为直接作用在人工边界上的等效荷载来实现波动输入，即把波动作用转换成人工边界节点作用力来实现波动的模拟[9]。在有限元计算中，截取的边界上要采用人工边界以模拟无限边界条件。根据杜修力等[11]的研究，运用波场分离技术，将总场在截取模型的底边界上分解为边界入射场和边界外行场, 侧边界上分解为自由场和散射场, 边界入射场或自由场可由连续介质力学模型解析计算得到, 边界外行场或散射场由人工边界条件模拟并由离散模型依据数值分析方法获得。将未知的散射场或边界外行场用总场减去自由场或边界入射场表示, 得到含外源作用的人工边界面L结点i方向的有限元运动方程为:

(1)

式中：{FL(t)}为施加在边界上的等效节点力。可对模型各个边界进行波场分解，求出总波场位移，进而根据胡克定律得到应力场，再乘以边界节点面积得到节点力。本文算例均采用二维平面有限元模型，输入波为S 波垂直入射，等效节点力计算公式如下[10-11]：

(2)

(3)

(4)

(5)

(6)

(7)

(8)

1.2 一致加速度激励原理及实现方法

根据D’Alembert原理，体系的运动方程可以写为：

(9)

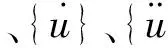
1.3 位移激励原理及实现方法

采用位移输入时，要用绝对位移来描述运动方程，体系的运动方程可以写为：

(10)

2 算例验证与分析

基于黏弹性边界条件，针对上述三种不同的地震动输入方法，进行不同边界条件和不同地震动输入方式的比较分析。边界条件的选择和地震动输入方法如表1所列。

表 1 边界条件和地震动输入选择

算例模型如图1所示，为二维弹性半空间模型，模型长取800 m，高取400 m，单元尺寸取为Δx=Δy=20 m，时间间隔取Δt=0.005 s。根据文献[12]模型材料参数取为：地层的弹性模量E=13.23 GPa，剪切模量G=5.292 GPa，泊松比μ=0.25，密度ρ=2 700 kg/m3，波速CS=1 400 m/s，CP=2 425 m/s。计算模型中的监测点分别为模型顶部中点A(0,400)、模型中心点B(0,200)和模型底边界中点O(0,0)。

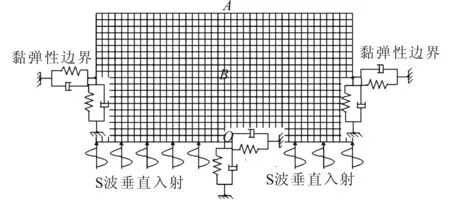
图1 有限元模型(工况一)Fig.1 Finite element model (Case 1)

地震波在地层中传播时会经过多次反射与折射，当传播至地表时已接近于垂直，因此在算例中采用从模型底部垂直入射一SV波[15]的入射形式，入射波方程为：

(2)

位移时程曲线如图2所示。

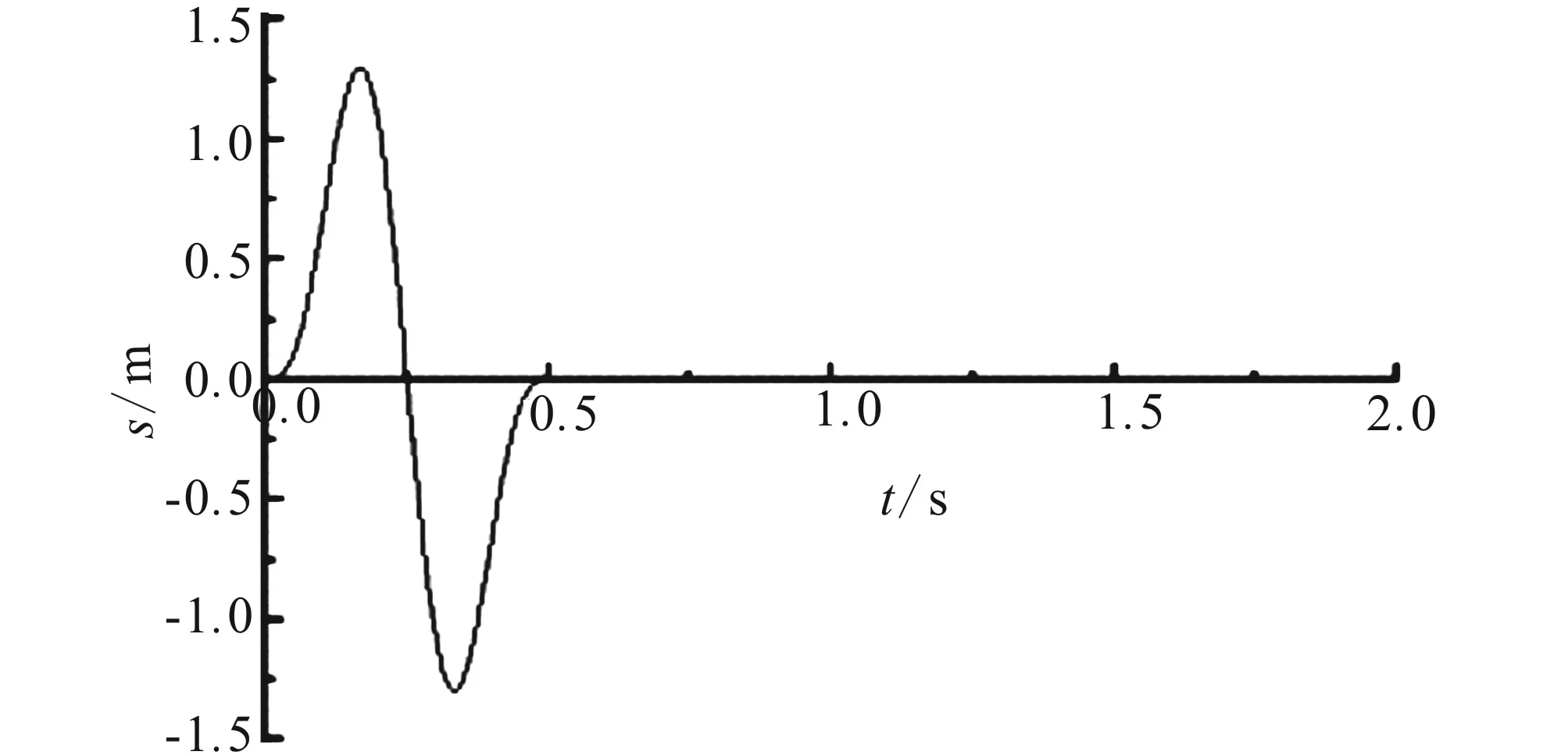
图2 入射波位移时程曲线图Fig.2 Displacement time-history curves of incident wave

2.1 计算结果对比分析

分别对各工况下监测点A、B、O的位移和应力进行对比分析。限于篇幅，这里只给出监测点A和B各工况的位移时程曲线和应力时程曲线，监测点O只将工况一和工况七的位移时程进行了比较，计算结果如图3所示。

2.2 位移分析

由图3中各工况位移时程曲线可以看出，在工况一中，剪切波经0.286 s传播至模型表面的A点并发生了反射，其位移幅值为入射波位移幅值的两倍，与一维弹性波动理论计算结果相一致，同时很好地模拟了波在介质中的传播效应。与工况一相比，工况二采用了目前比较常用的加速度输入方法，它不能模拟波在弹性介质中的传播效应，因此从一开始模型表面的A点便发生位移，且在A点位移幅值略大于工况一的位移幅值，而B点位移幅值及变化情况与A点相似；工况三能够模拟波在介质中的传播效应，但位移幅值与工况一相比明显偏小；工况四中，位移一开始没有达到最大值，而是经过一次震荡后达到了最大值3.33m，超过了工况一的最大值2.73m，且达到峰值后经过几次震荡，反射波才被完全吸收，达到稳定；工况五与工况三一样，能够模拟波的传播效应，但位移值幅值偏小，且要经过几次震荡才能趋于稳定；工况六位移偏小；对于工况七，从监测点A、B和O的位移时程曲线可以看出，波传播到模型顶部时发生反射，当传至模型底部时被底部的黏弹性边界完全吸收，与工况一基本吻合，既模拟了波的传播效应，也有较高的精度。分析其原因是当剪切波垂直入射模型底部时，波垂直向上传播，同时左右震动，引起了质点水平方向的位移，而工况七正好与剪切波引起的边界条件相符，因此具有较高的精度。

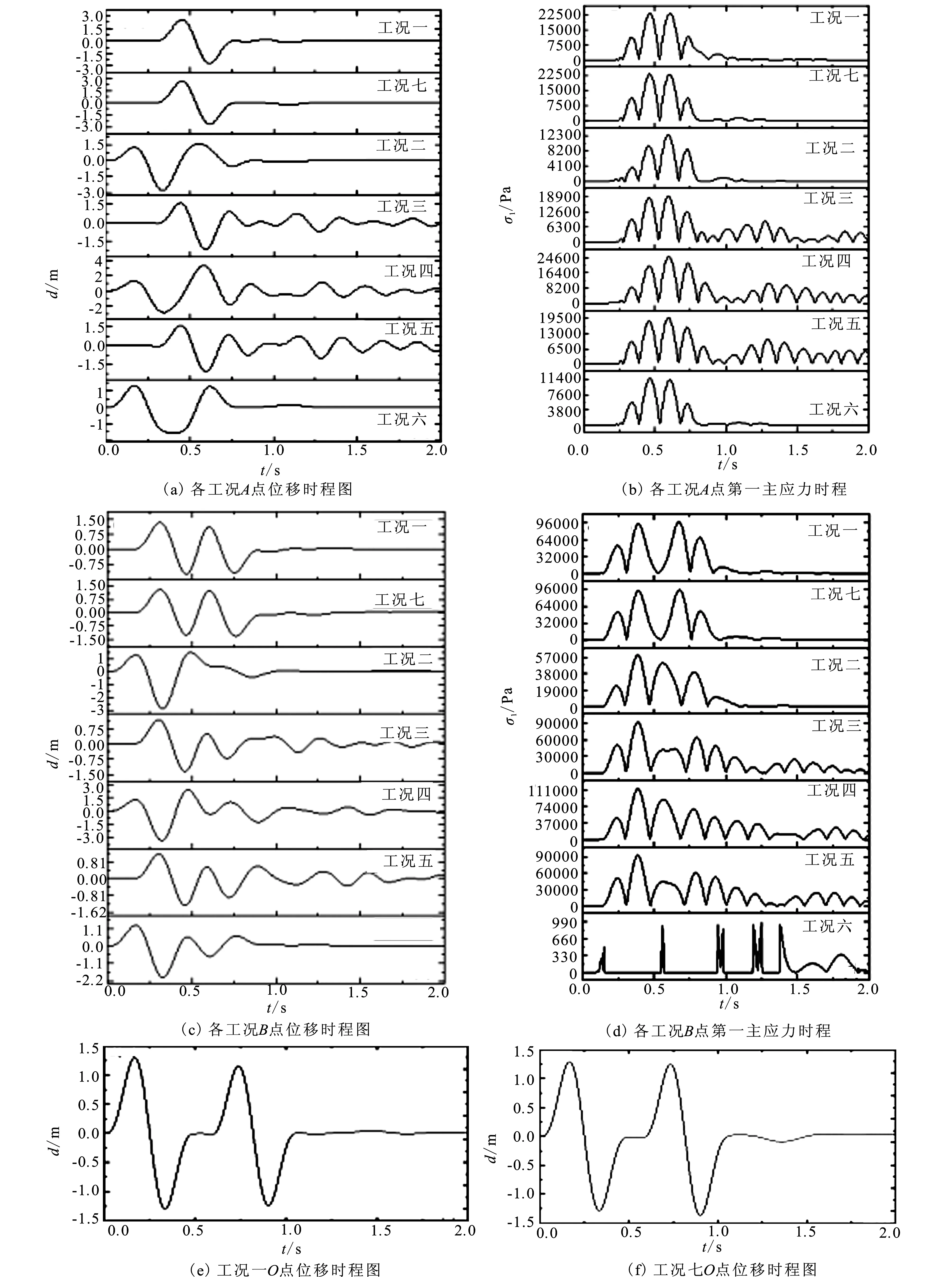
图3 监测点位移和应力时程Fig.3 Displacement and the first principal stress time-history curves of monitoring points

2.3 应力分析

由图3中各工况第一主应力时程曲线可以看出，工况一、工况二、工况三、工况六和工况七的第一主应力变化趋势一致(工况六B点除外)，但工况二、工况三、工况五和工况六应力值较工况一相对较小，只有工况七的第一主应力和工况一几乎相同，当波传播至模型底部时被底部边界完全吸收，无任何震荡发生。而工况四的主应力与工况一相比偏大，且在后面出现了震荡。因此可以看出，采用工况七的方法可以得到很好的结果。

从以上对位移和应力的分析可以看出：采用工况七的边界条件和地震动输入方法，不论是在位移上还是在应力上都能够与工况一相一致，但与工况一相比，其更容易实现、效率明显更高。因此，在二维地下结构抗震分析中可以采用工况七的方法。

3 结论

通过对不同边界条件和不同地震动输入方法下七种工况的位移时程和应力时程进行比较研究发现：

(1) 采用三边黏弹性边界条件和应力输入方法，既可以较好地模拟对散射波的吸收，也能模拟半无限地基的弹性恢复能力，但编程实现时要在侧边界施加等效节点荷载，较为麻烦。

(2) 当采用两边黏弹性边界条件、底部固定边界条件，地震动输入为加速度时程时，计算出的位移和应力都偏大，计算精度欠佳，且不能模拟波在介质中的传播效应。

(3) 当采用位移输入时，虽然可以模拟波在介质中的传播效应，但计算结果偏小，且要经过几次震荡后才能将反射波完全吸收。

(4) 当采用底部黏弹性、两侧竖向位移约束、底面应力输入的方法时，计算结果既具有较高的计算精度，又易于编程实现，只需在模型底部施加等效节点荷载，免去了侧边界等效节点荷载的施加，而在编程实现的过程中，恰恰是侧边界的等效节点荷载较难施加。因此采用工况七的边界条件和地震动输入方法可以大大减小工作量，同时为地下工程抗震分析中黏弹性边界条件的应用提供便利。

)

[1] 赵武胜,陈卫忠,郑朋强,等.地下工程数值计算中地震动输入方法选择及实现[J].岩石力学与工程学报,2013,32(8):1579-1587.ZHAOWu-sheng,CHENWei-zhong,ZHENGPeng-qiang,etal.ChoiceandImplementationofSeismicWaveInputMethodinNumericalCalculationforUndergroundEngineering[J].ChineseJournalofRockMechanicsandEngineering,2013,32(8):1579-1587. (inChinese)

[2] Lysmer J，Kulemeyer R L.Finite Dynamic Model for Infinite Media[J].Journal of Engineering Mechanics，ASCE，1969，95(4)：859-877.

[3] Deeks A J，Randolph M F.Axisymmetric Time-domain Transmitting Boundaries[J].Journal of Engineering Mechanics，ASCE， 1994，120(1)：25-42.

[4] 刘晶波,吕彦东.结构一地基动力相互作用问题分析的一种直接方法[J].土木工程学报,1998,31(3):55-64. LIU Jing-bo，LV Yan-dong.A Direct Method for Analysis of Dynamic Soil-structure Interaction[J].China Civil Engineering Journal，1998，31(3)：55-64.(in Chinese)

[5] 刘晶波,杜义欣,闫秋实.黏弹性人工边界及地震动输入在通用有限元软件中的实现[J].防灾减灾工程学报,2007,27(增刊):37-42. LIU Jing-bo,DU Yi-xin,YAN Qiu-shi.Application of Viscous-spring Artificial Boundary and Seismic Input in General Finite Element Software[J].Journal of Disaster Prevention and Mitigation Engineering,2007,27(Supp):37-43.(in Chinese)

[6] 刘晶波,谷音,杜义欣.一致黏弹性人工边界及黏弹性边界单元[J].岩土工程学报,2006,28(9):1070-1074. LIU Jing-bo,GU Yin,DU Yi-xin.Consistent Viscous-spring Artificial Boundaries and Viscous-spring Boundary Elements[J].Chinese Journal of Geotechnical Engineering,2006,28(9):1070-1074. (in Chinese)

[7] 单华廷，李立云，杜修力.地下结构地震反应分析中材料非线性的影响[J].西北地震学报,2011,33(增刊):360-365. SHAN Hua-ting,LI Li-yun,DU Xiu-li.Effect of the Material Nonlinear Property on Seismic Response Analysis of Underground Structure[J].Northwestern Seismological Journal,2011,33(Supp):360-365. (in chinese)

[8] 李鹏,刘光磊,宋二祥.饱和地基中地下结构地震反应若干问题研究[J].地震工程学报,2014,36(4)：843-849. LI Peng,LIU Guang-lei,SONG Er-xiang.Research on Seismic Response of Underground Structures in Saturated Foundation[J].China Earthquake Engeering Journal,2014,36(4)：843-849. (in Chinese)

[9] 高峰,孙常新,赵冯兵.地下结构波动法与振动法的对比[J].重庆交通大学学报:自然科学版,2012,31(4):764-768. GAO Feng,SUN Chang-xin,ZHAO Feng-bing.Contrast of Wave and Vibration Methods for Underground Structure[J].Journal of Chongqing Jiaotong University:Natural Science,2012,31(4):764-768.(in Chinese)

[10] 汪精河,周晓军,毛露露,等.地下结构抗震分析中地震动输入方法的比较研究[J].现代隧道技术,2015,52(3):103-108. WANG Jing-he,ZHOU Xiao-jun,MAO Lu-lu,et al.Comparative Study of Earthquake Input Methods for the Seismic Analysis of Underground Structures[J].Modern Tunnelling Technology,2015,52(3):103-108.(in Chniese)

[11] 杜修力, 赵密.基于黏弹性边界的拱坝地震反应分析方法[J].水利学报,2006,37(9):1063-1068. DU Xiu-li,ZHAO Mi.Analysis Method for Seismic Response of Arch Dams in Time Domain Based on Viscous-spring Artificial Boundary Condition[J].Journal of Hydraulic Engineering,2006,37(9):1063-1068.(in Chinese)

[12] 刘晶波,李彬.三维黏弹性静-动力统一人工边界[J].中国科学:E 辑,2005,35(9):966-980. LIU Jing-bo,LI Bin.3D Visco-elastic Static-dynamic Uniform Artificial Boundary[J].Science in China:Ser. E,2005,35(9):966-980.(in Chinese)

[13] 王新敏.ANSYS结构动力分析与应用[M].北京：人民交通出版社,2014. WANG Xin-min.Structural Dynamic Analysis and Application with ANSYS[M].Beijing：China Communications Press,2014. (in Chinese)

[14] 陈灯红,杜成斌,苑举卫 基于ABAQUS的黏弹性边界单元及在重力坝抗震分析中的应用[J].世界地震工程,2010,26(3):127-132. CHEN Deng-hong,DU Cheng-bin,YUAN Ju-wei.Viscous-spring Boundary Element Based on Abaqusand Application to Dynamic Analysis of Agravity Dam[J].World Earthquake Engineering,2010,26(3):127-132.(in Chinese)

[15] 贺向丽.高混凝土坝抗震分析中远域能量逸散时域模拟方法研究[D].南京:河海大学,2006. HE Xiang-li.Study on Time-domain Simulating Method of Far Field Energy Dissipation in Seismic Analysis of High Concrete Dams[D].Nanjing:Hohai University,2006.(in Chinese)

Earthquake Input Method and Selection of Boundary Conditions Based on Viscoelastic Boundaries

SUN Wei-yu1,2, OU Er-feng1,2, YAN Song-hong1,3

(1.KeyLaboratoryofRoad&BridgeandUndergroundEngineeringofGansuProvince,LanzhouJiaotongUniversity,Lanzhou730070,Gansu,China; 2.SchoolofCivilEngineering,LanzhouJiaotongUniversity,Lanzhou730070,Gansu,China; 3.EngineeringLaboratoryofMechenicsApplicationofRailwayTransportationofGansuProvince,LanzhouJiaotongUniversity,Lanzhou730070,Gansu,China)

In the seismic design and analysis of underground structures, in order to select the appropriate boundary conditions and earthquake input types, we conduct simulation experiments on an underground semi-infinite body model, which is vertically incident by a shear wave. The main results are as follows: (1) Considering three viscoelastic artificial boundaries (two lateral boundaries and the bottom boundary) and using stress as the seismic motion input, the model can not only simulate the absorption of the scattered waves but also the elastic recovery of the semi-infinite foundation. However, these model conditions are unrealistic with regard to the equivalent nodal loads on both the two lateral boundaries and the bottom boundary. (2) If the two lateral boundaries are viscoelastic artificial boundaries, the bottom boundary is fixed, and the acceleration time history is used as the seismic motion input, the displacements and stresses are overestimated by the model. In addition, the model cannot simulate the propagation effect of the wave in the medium. If we use the displacement time history as the seismic motion input, although the propagation effect of the wave can be simulated in the medium, the displacements and stresses are underestimated and the reflection wave can only be completely absorbed after several shocks. (3) If the bottom boundary is a viscoelastic artificial boundary and the two lateral boundaries are vertical displacement constraint boundaries, exerting nodal loads on the bottom boundary can be obtained with great accuracy. Moreover, the model is simple to use in ANSYS by APDL programming because only the equivalent nodal loads on the bottom boundary must be input. Therefore, it is a simple method for determining viscoelastic artificial boundaries in the anti-seismic analysis of underground engineering.

underground engineering; viscoelastic boundary; earthquake input; boundary condition; ANSYS

2016-08-30 基金项目：甘肃省科技计划资助(1310RJZA041)；国家自然基金项目(51268030)

孙纬宇(1988-)，男，甘肃天水人，博士研究生，主要从事黄土隧道抗震方面研究。E-mail:448221362@qq.com。

TU311.3

A

1000-0844(2016)06-0929-06

10.3969/j.issn.1000-0844.2016.06.0929