小应变硬化模型(HSS)在Rayleigh波作用下场地响应分析中的应用

施有志, 林树枝, 杨荣华

(1.厦门理工学院土木工程与建筑学院,福建 厦门 361021; 2.上海交通大学船舶海洋与建筑工程学院,上海 200240;3.厦门市建设局,福建 厦门 361003)

小应变硬化模型(HSS)在Rayleigh波作用下场地响应分析中的应用

施有志1,2, 林树枝3, 杨荣华1

(1.厦门理工学院土木工程与建筑学院,福建 厦门 361021; 2.上海交通大学船舶海洋与建筑工程学院,上海 200240;3.厦门市建设局,福建 厦门 361003)

小应变硬化模型(HSS); 瑞利阻尼; Rayleigh波; 地震动力响应; 有限元动力分析

0 引言

土体受冲击荷载或地震作用时,巨大的能量在地基中产生强烈的震动,并以波动的形式从震源向四周传播,其中包括压缩波P波、剪切波S波和以Rayleigh波为主的面波组成。体波(包括P波和S波)从波源沿着一个半球波阵面径向向外传播,而Rayleigh波则沿着一个圆柱波径向向外传播。Miller等[1]曾研究了三种弹性波占地震总输入能量的百分比,发现Rayleigh波占67.3%,S波占25.8%,P波占6.9%。由于Rayleigh波能量分布一般仅限于距离半空间自由表面两倍其波长范围的岩土层内,因此它对浅埋地下结构的地震反应具有重要影响。李恒等[2]、陈永新等[3]研究地表岩土层特点对地震动特性的影响,但未对Rayleigh波的影响进行探讨。目前对Rayleigh波的研究主要体现在岩土参数反演及物探等方面的应用[4-5];另有学者研究冲击荷载产生的Rayleigh波的作用机制[7-8];Makris[9-10]研究Rayleigh波作用下桩的响应;蒋东旗等[11-12]研究远场地震动对桩基响应的影响。上述研究都将Rayleigh波考虑为简谐振动输入进行分析。岳庆霞等[13]提出了近似Rayleigh地震波的概念,利用已有的地震记录,将之视为水平方向的波动,而后利用傅里叶变换得到竖直方向的波动,并考虑沿深度方向的衰减,从而得到整个位移场;罗韬[14]通过小波变换和傅里叶变换对地震波进行低频重构,得到整个Rayleigh波场。上述构建的Rayleigh波不是通过波的干涉形成,与实际的地震动有一定的差异。有限元动力分析仍是研究Rayleigh波对土体动力响应的主要手段。土体由于土粒间的摩擦、孔隙水和空气的黏滞性,需要引入阻尼来模拟土体在循环加载作用下的阻尼特性。在各种阻尼模型中使用最广泛的是Rayleigh阻尼[15],研究者们围绕着Rayleigh阻尼的取值,亦目标频率的选取,提出了多种不同的方法[16-19],但尚未形成统一的认识。

土体硬化模型(HSS)是高级本构模型,能够考虑土体在循环加载下的滞回效应,在动力计算中,HSS模型的滞回行为就会引起阻尼。为了研究HSS模型中本身的滞回环特性,本文以厦门地区浅层的素填土及粉质黏土为研究对象,采用有限元动力分析,输入变化的小应变参数,考察HSS模型的小应变参数对场地动力响应的影响,并与土体采用摩尔-库伦模型结合Rayleigh阻尼的计算结果进行对比。研究成果有利于利用HSS模型研究Rayleigh波对浅埋结构物的动力响应分析以及阻尼的设置方法。

1 HSS模型简介

HSS模型是以HS模型为基础,考虑应变历史的影响并结合修正的Hardin-Drnevich[20]剪切模量关系式提出的一种能反应土体小应变特性的本构模型。小应变土体硬化模型(HSS)能够考虑土体在循环加载下的滞回效应,滞回环的大小取决于相应的应变幅值的大小。在动力计算中,HSS模型的滞回行为就会引起阻尼,滞回阻尼量取决于施加的荷载幅值和相应的应变幅值。HSS模型产生的最大滞回阻尼则取决于G0/Gur,其中G0为初始剪切刚度,Gur为卸载重加载剪切模量,该刚度比越大,则最大滞回阻尼也越大。

通常而言,地震能在土体中引起小应变,土体表现出高剪切刚度G0,当剪应变γ幅值增加而使能量消耗增加时刚度会降低。要考虑上述表征材料小应变行为的三个参数,需要使用基于土体硬化模型(Hardening Soil model,HS)拓展而来的小应变土体硬化模型(HS small model,HSS)。HS模型已经基于幂率参数m考虑了土体刚度的应力相关性,在此基础上,HSS模型引入了另外两个参数,即表征小应变水平下的高刚度特性的参数G0和表征G衰减至初始G0的70%时的剪应变的参数γ0.7。

HSS模型中土体的应力相关性采用下式表示:

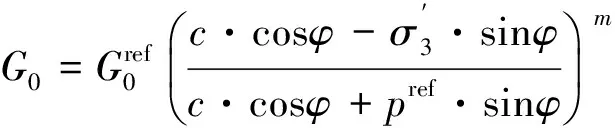
(1)

土体典型的滞回行为如图1所示。Gs为割线模量;Gt为切线剪切模量。可见初始加载曲线的初始切线和割线刚度与最大剪切刚度G0一致。随着剪应变增大,刚度发生衰减。当加载方向发生反转,刚度从相同的G0出发,然后降低至下一次加载反转。

图1 HSS模型的滞回行为Fig.1 Hysteretic behavior of HSS model

2 厦门地区典型土层HSS模型中阻尼参数研究

2.1 模型建立

建立有限元模型如图2。沿地表距冲击荷载作用点分别为40、50、60、70及80 m处设5个位移监测点(图3)。

模型对称轴上受到一个集中荷载作为动力输入。动力荷载采用随时间按三角形变化的荷载来模拟,自0.05 s之后开始施加荷载,荷载持续时间取0.025 s,荷载振幅取50 kN(图4)。

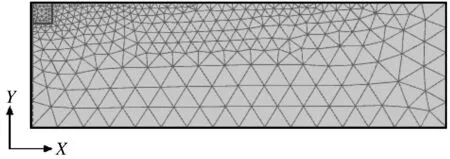
图2 有限元模型Fig.2 Finite element model

图3 位移监测点布置Fig.3 Distribution of displacement monitoring points

图4 冲击荷载定义Fig.4 Definition of impact loading

在有限元动力计算中,为了尽量避免应力波在模型边界上的反射导致计算结果失真,需要将模型边界取得足够远,但这会大大增加单元数量和计算成本,因此需引入人工边界。本文在模型底部和Xmax、Ymax边界上引入吸收边界,来确保模型边界上的应力波被吸收而不发生反弹。

2.2 参数取值

以厦门地区浅层土层为例,概化出素填土及粉质黏土两种土层为研究对象。土体本构采用HSS模型,模型基本输入参数见表1。

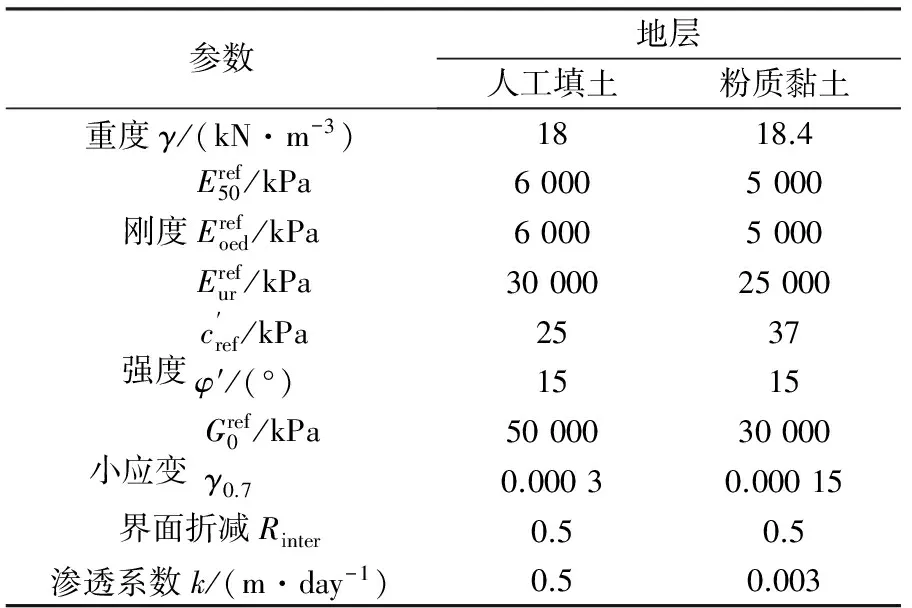
表1 两类典型土体HSS模型基本输入参数

表中参数的定义如下:

γ:天然重度;

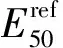
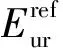
φ′:有效内摩擦角;

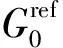
γ0.7:当割线剪切模量Gsecant衰减为0.7倍的初始剪切模量G0时对应的剪应变。

当土体本构采用摩尔-库伦模型时,参数取值如下:素填土剪切波波速vS=135 m/s,压缩波波速vP=325 m/s,重度γ=18 kN/m3,黏聚力c=15 kN/m2,摩擦角φ=25°;粉质黏土剪切波波速vS=102 m/s,压缩波波速vP=227 m/s,重度γ=18.4 kN/m3,黏聚力c=37 kN/m2,摩擦角φ=15°。

2.3 计算方案

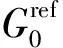
C=αM+βK

式中:α和β分别为质量比例阻尼系数和刚度比例阻尼系数。

将“MC+Rayleigh阻尼”与“HSS+滞回环阻尼”计算结果进行对比分析。针对素填土和粉质黏土的计算方案如表2所列。

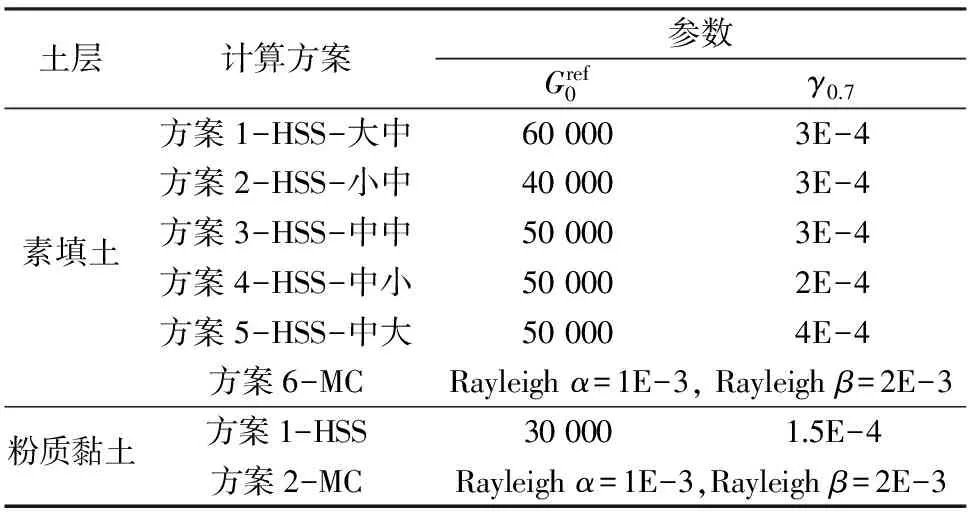
表2 计算方案

图5 HSS模型小应变阻尼曲线Fig.5 Small strain damping curve of HSS model

图6 Rayleigh阻尼曲线Fig.6 Rayleigh damping curve

2.4 计算结果

(1) 素填土

以距冲击荷载水平距离50 m处的地表点竖向位移为例,对场地动力响应特征进行分析,各计算方案下该点竖向位移-时间曲线如图7～图9所示。

图10所示为素填土计算方案3与方案6得出的不同时刻网格变形形态图。由图10可以看出:使用“HSS+滞回环”与使用“MC+Rayleigh阻尼”得到的波速是基本一致的,在加卸载循环中MC模型表现出了弹性行为,反弹较为明显,HSS模型则因其滞回环效应累积了塑性变形,对材料阻尼的考虑更为符合实际。

(2) 粉质黏土

以距冲击荷载水平距离50 m处的地表点竖向位移为例,对场地动力响应特征进行分析,各计算方案下该点竖向位移-时间曲线如图11所示。

从图11可以看到,采用“MC+Rayleigh阻尼”时,波动很快趋于稳定,几乎没有发生振荡;但采用带有滞回环的HSS模型时,位移波动出现大幅明显振荡,波动平稳下来要比Rayleigh阻尼慢得多,且存在残余变形。由于HSS模型的小应变刚度只能考虑滞回环阻尼,仍然不能完全体现材料阻尼的影响,因此其使得振幅较MC更大。

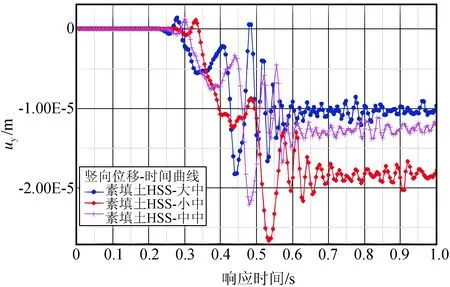
图7 γ0.7不变增大时的场地动力响应(素填土)Fig.7 Site dynamic response when γ0.7 remains and rises (plain fill)

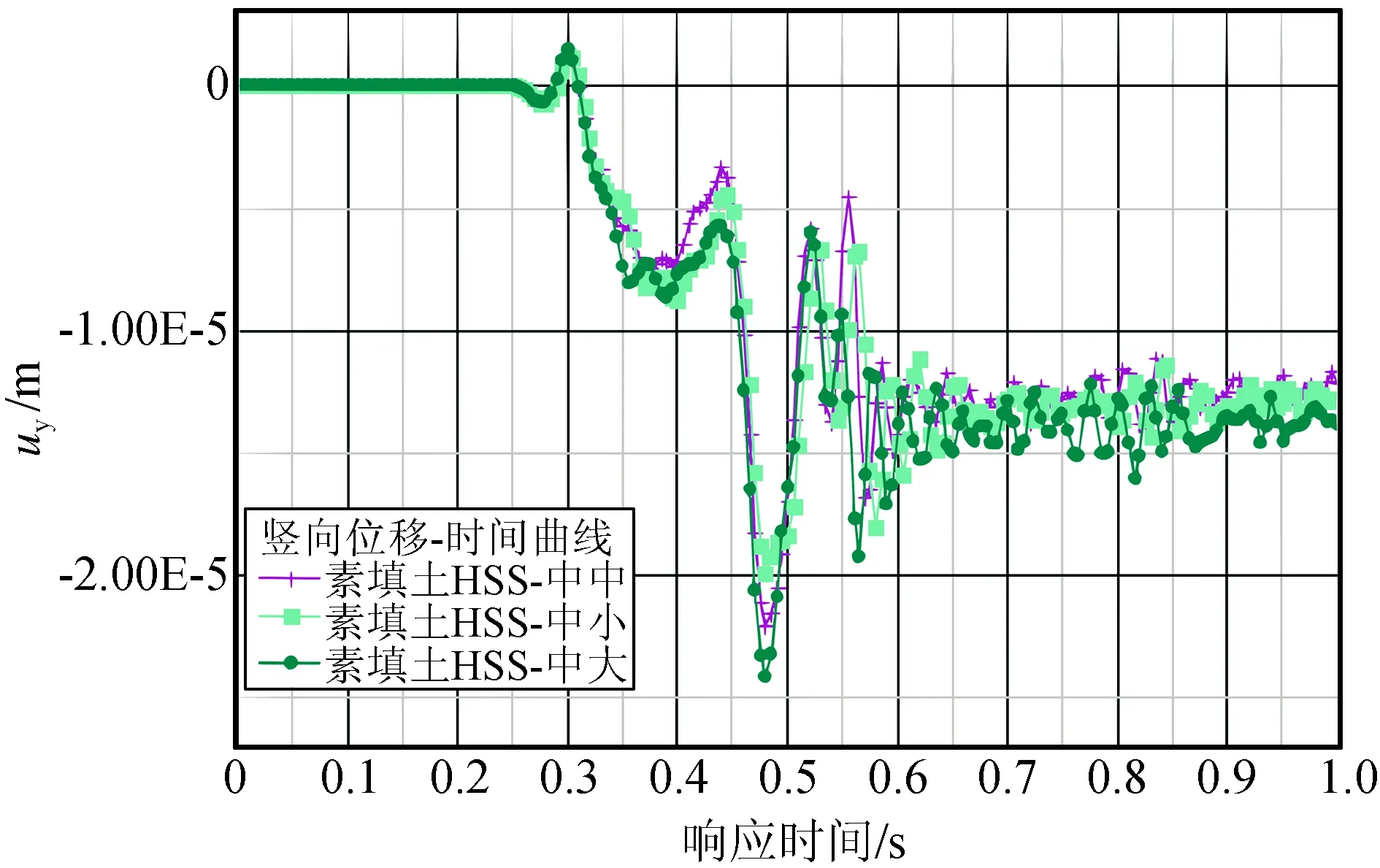
图不变γ0.7变化时的场地动力响应(素填土)Fig.8 Site dynamic response when γ0.7 changes and remains (plain fill)

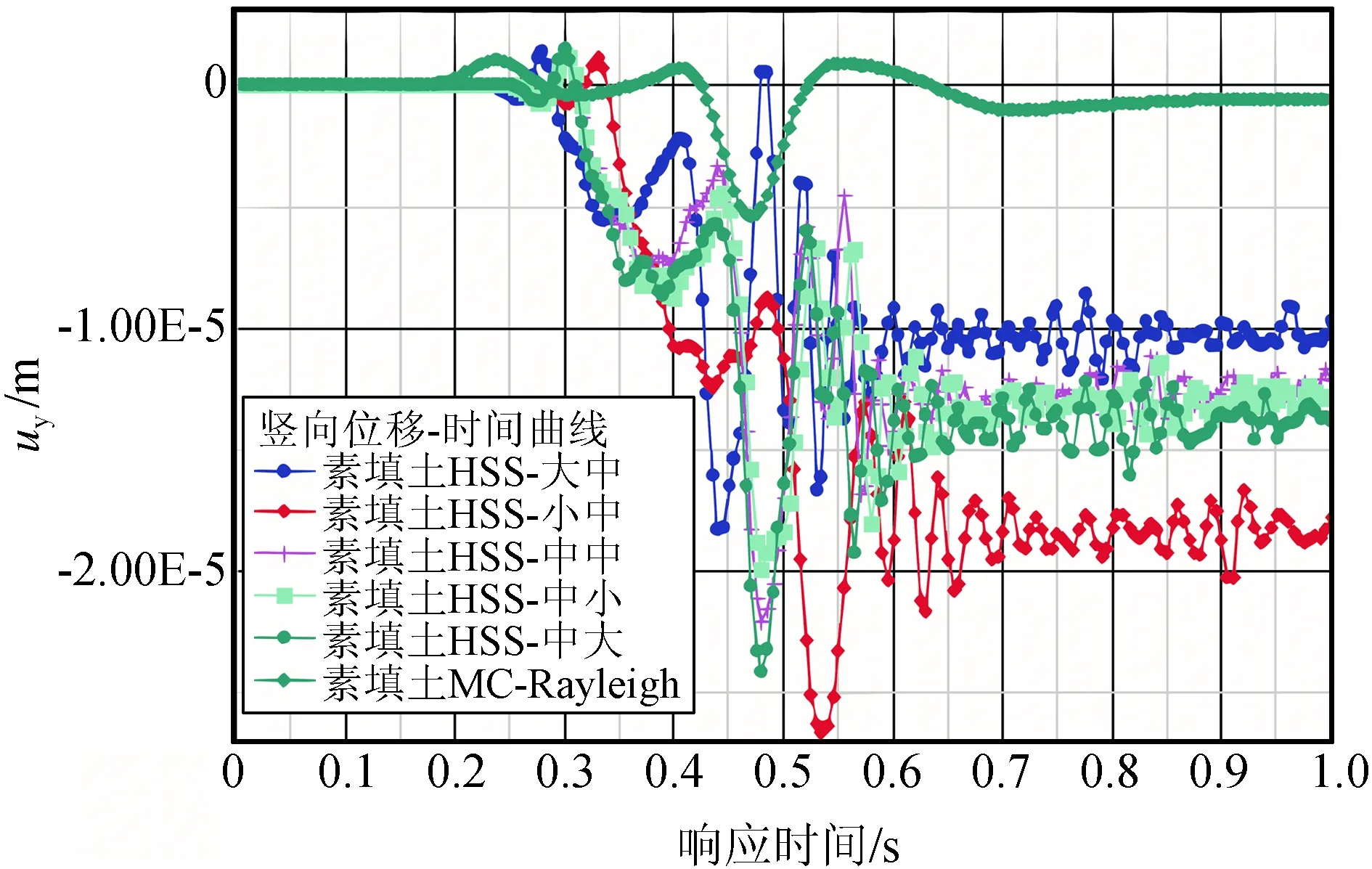
图9 “HSS +滞回环”与“MC+Rayleigh阻尼”动力响应曲线对比(素填土)Fig.9 “HSS+hysteresis loop” and “MC+Rayleigh damping” dynamic response curve comparison(plain fill)

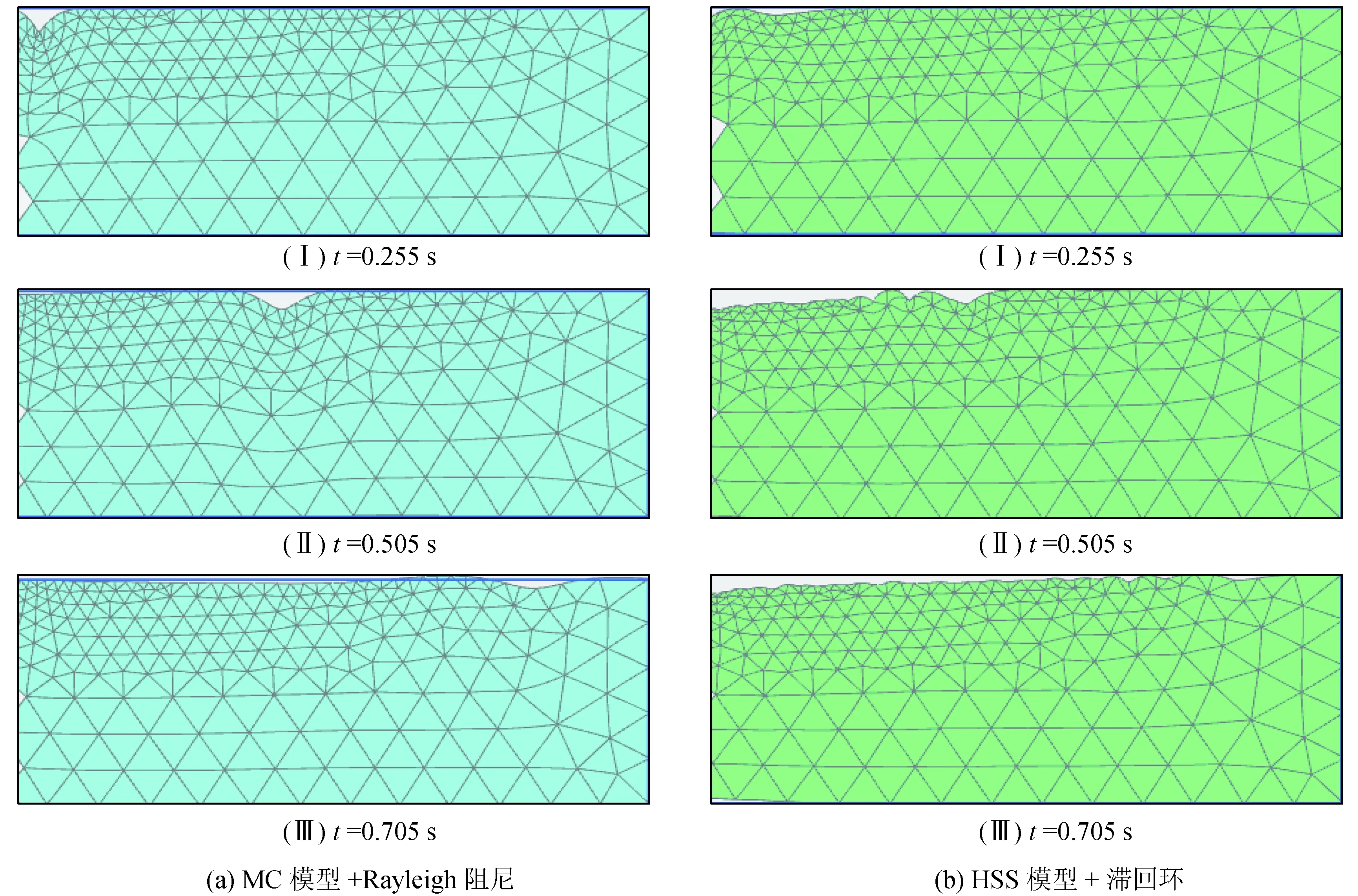
图10 “MC+Rayleigh阻尼”与“HSS+滞回环”场地动力响应对比(素填土)Fig.10 “MC+Rayleigh damping” and “HSS+hysteresis loop” site dynamic response comparison (plain fill)

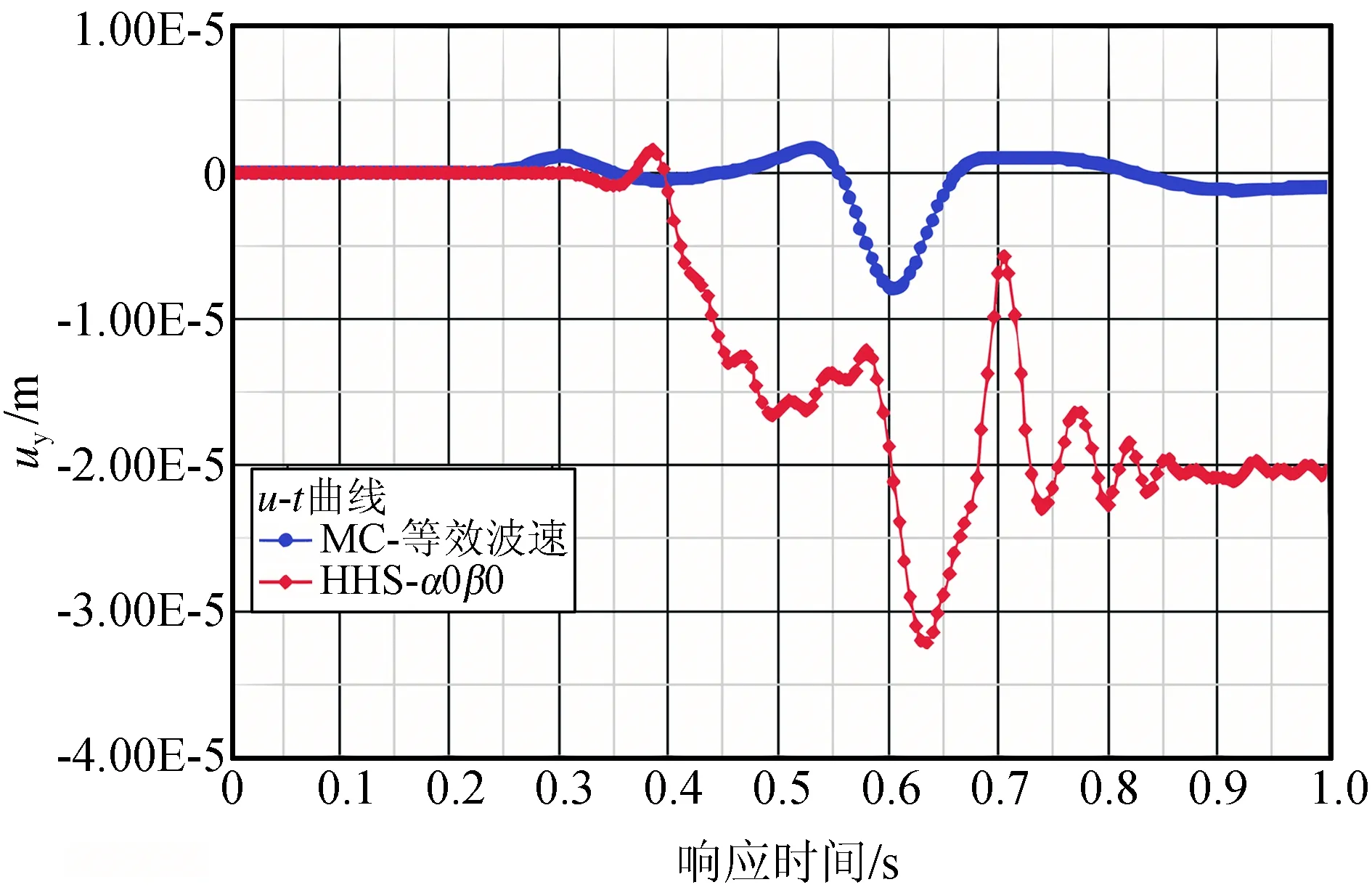
图11 “HSS +滞回环”与“MC+Rayleigh阻尼”动力响应曲线对比(粉质黏土)Fig.11 “HSS+hysteresis loop” and “MC+Rayleigh damping” dynamic response curve comparison(silty clay)

3 结 语

本文以厦门地区受Rayleigh波影响显著的场地浅层典型土体素填土和粉质黏土为研究对象,采用有限元动力分析,土体本构采用小应变硬化模型(HSS),利用模型本身的滞回环特性,输入变化的小应变参数,考察HSS模型的小应变参数对场地动力响应的影响,并与土体采用摩尔-库伦模型结合Rayleigh阻尼(“MC+Rayleigh阻尼”)的计算结果进行对比,得出如下结论:

(2) 与“MC模型+Rayleigh阻尼”动力响应结果相比,“HSS模型+滞回环”得到的动力响应波动更加剧烈,更重要的是HSS模型能够给出残余变形量;而MC模型+Rayleigh阻尼则由于MC模型为理想弹塑性模型,在卸载重加载条件下表现为纯弹性行为,无法反映出卸载重加载过程中塑性应变的积累及其累积阻尼效应,这是即便使用Rayleigh阻尼也无法考虑的情况。

(3) HSS模型还不能够全面反映循环加载作用下塑性体积应变的累积。在小幅振动情况下,即使采用小应变土体硬化模型也不能完全体现材料阻尼,因此在考虑滞回阻尼的基础上,仍然建议借助Rayleigh阻尼来更加全面地模拟土体的实际阻尼特性。

References)

[1] Miller G F,Pursey H.On the Partition of Energy between Elastic Waves in a Semi-infinite Solid[J].Proceedings of the Royal Society A,1955,233(233):55-69.

[2] 李恒,张静波,吴建超.软夹层和硬夹层对地表地震动特性的影响[J].地震工程学报,2014,36(3):441-445. LI Heng,ZHANG Jing-bo,WU Jian-chao.Effects of Soft and Hard Interlayers on Ground Motion Characteristics[J].China Earthquake Engineering Journal,2014,36(3):441-445.(in Chinese)[3] 陈永新,迟明杰,李小军.地表岩土层对地震动特性的影响分析[J].地震工程学报,2015,37(3):743-747. CHEN Yong-xin,CHI Ming-jie,LI Xiao-jun.Effect of over Laying Rock and Soil Layers on Ground Motion Characteristics[J].China Earthquake Engineering Journal,2015,37(3):743-747.(in Chinese)

[4] 卞鹏,王媛,王笃强.有障碍物地基瑞利波频散曲线的特征研究[J].山东大学学报:工学版,2012,42(1):99-103. BIAN Peng,WANG Yuan,WANG Du-qiang.Research on the Frequency Dispersion Curve of the Rayleigh Wave in the Foundation with an Obstacle[J].Journal of Shandong University:Engineering Science,2012,42(1):99-103.(in Chinese)

[5] 唐平祥.瑞利波法在公路地基中的应用[J].公路工程,2012,37(3):209-212. TANG Ping-xiang.Rayleigh Wave Method for Soil Characterization[J].Highway Engineering,2012,37(3):209-212.(in Chinese)

[6] 黄达,金华辉.土石比对碎石土强夯地基加固效果影响规律瑞利波检测分析[J].岩土力学,2012,33(10):3067-3072. HUANG Da,JIN Hua-hui.Influences of Soil-rock Ratio on Foundation with Detritus Soil under Dynamic Compaction Based on Rayleigh Wave Detection[J].Rock and Soil Mechanics,2012,33(10):3067-3072.(in Chinese)

[7] 牛志荣,杨桂通.冲击荷载下土体位移特征研究[J].岩土力学,2005,26(11):52-57. NIU Zhi-rong,YANG Gui-tong.Studies on the Displacement of Soils Subjected to the Impact Loading[J].Rock and Soil Mechanics,2005,26(11):52-57.(in Chinese)

[8] 牛志荣,路国运.土体受冲击时Rayleigh波作用机制探讨[J].岩土力学,2009,30(6):1583-1589. NIU Zhi-rong,LU Guo-yun.Discussion on Mechanism and Effect of Rayleigh Wave on Soil Subjected to Impact Loading[J].Rock and Soil Mechanics,2009,30(6):1583-1589.(in Chinese)

[9] Makris N.Soil-pile Interaction During the Passage of Rayleigh Waves:An Analytical Solution[J].Earthquake Engineering and Structural Dynamics,1994,23(2):153-167.

[10] Makris N,Badoni D.Seismic Response of Pile Groups under Oblique-shear and Rayleigh Waves[J].Earthquake Engineering & Structural Dynamics,1995,24(4):517-532.

[11] 蒋东旗,王立忠,陈云敏.远场地震引起的单桩横向位移和内力[J].岩土工程学报,2003,25(2):174-178. JIANG Dong-qi,WANG Li-zhong,CHEN Yun-min.Lateral Displacement and Internal Force of Single Pile Induced by Far-fieldearthquake[J].Chinese Jounal of Geotechnical Engineering,2003,25(2):174-178.(in Chinese)

[12] 蒋东旗,郝玉龙,陈云敏.远场地震作用下桩间横向动力相互作用的研究[J].地震工程与工程振动,2004,24(4):170-176. JIANG Dong-qi,HAO Yu-long,CHEN Yun-min.Lateral Dynamic Pile-pile Interaction Induced by Far-field Earthquake[J].Earthquake Engineering and Engineering Vibration,2004,24(4):170-176.(in Chinese)

[13] 岳庆霞,李杰.近似Rayleigh地震波作用下地下综合管廊响应分析[J].防灾减灾工程学报,2008,28(4):409-416. YUE Qing-xia,LI Jie.Response Analysis of Utility Tunnel in Earthquake of Approximate Rayleigh Waves[J].Journal of Disaster Prevention and Mitigation Engineering,2008,28(4):409-416.(in Chinese)

[14] 罗韬.基于小波变换的Rayleigh地震波及地下综合管廊地震响应研究[D].济南:山东建筑大学土木工程学院,2013. LUO Tao.Rayleigh Wave Research Based on Wavelet Transform and Response of the Utility Tunnel[D].Jinan:Shandong Jianzhu University,School of Architecture and Construction,2013.(in Chinese)

[15] 潘旦光.直接确定Rayleigh阻尼系数的一种优化方法[J].工程力学,2013,30(9):16-21. PAN Dan-guang.An Optimization Method for the Direct Determination of Rayleigh Damping Coefficients[J].Engineering Mechanics,2013,30(9):16-21.(in Chinese)

[16] Duhee P,Youssef M A.Soil Damping Formulation in Nonlinear Time Domain Site Response Analysis[J].Journal of Earthquake Engineering,2004,8(2):249-274.

[17] Hudson M,Idriss I M,Beikae M.User Manual for QUAD4M:A Computer Program to Evaluate the Seismic Response of Soil Structures Using Finite Element Procedures and Incorporating a Compliant Base[D].Berkeley:University of California,1994,52-80.

[18] Annie O L,Jonathan P S,Youssef M A,et al.Use of Exact Solutions of Wave Propagation Problems to Guide Implementation of Nonlinear Seismic Ground Response Analysis Procedures[J].Journal of Geotechnical and Geoenvironmental Engineering,2007,133(11):1385-1398.

[19] Nozomu Y,Satoshi K,Iwao S,et al.Equivalent Linear Method Considering Frequency Dependent Characteristics of Stiffness and Damping[J].Soil Dynamics and Earthquake Engineering,2002,22(3):205-222.

[20] Hardin B O,Drnevich V P.Shear Modulus and Damping in Soils[J].Journal of the Soil Mechanics and Founda-tions Division,1972,98(7):667-692.

Application of Hardening Small Strain Model in the Site Response Analysis under Rayleigh Wave Excitation

SHI You-zhi1,2, LIN Shu-zhi3, YANG Rong-hua1

(1.SchoolofCivilEngineeringandArchitecture,XiamenUniversityofTechnology,Xiamen361021,Fuyuan,China; 2.SchoolofNavalArchitecture,Ocean&CivilEngineering,ShanghaiJiaotongUniversity,Shanghai200240,China; 3.XiamenConstructionBureau,Xiamen361003,Fujian,China)

This study examines the dynamic response characteristics of surface waves mainly comprising Rayleigh waves in surface soils under impact and seismic loads. Moreover, the study analyzes, through numerical simulation, the settling methods of soil layer damping. The research area for this study is the shallow plain fill and silty clay of the Xiamen area. The model was generated using finite element dynamic analysis, with a hardening small strain model (HSS) for soil constitutive. The hysteresis characteristics of the model allowed the input of different small strain parameters to study the influence of HSS model's small strain parameters on site dynamic response. Results were then compared with the combined Mohr-Coulomb (MC) model and Rayleigh damping model (MC + Rayleigh damping). The study shows that when using HSS model with hysteresis, the wave speed increases with increases in the initial shear modulus; however, amplitude and residual deformation decline. While the HSS model can reach the residual deformation value, "MC + Rayleigh damping" cannot. This reflects the accumulation of plastic strain and the damping effect during the process of unloading and reloading as the constitutive model is an ideal elastic-plastic model that demonstrates pure elastic behavior under the conditions of unloading and reloading. However, as the HSS model cannot fully reflect the accumulation of plastic volume strain under the effect of reloading and taking hysteresis damping into consideration, the use of the Rayleigh damping model is advised to allow full simulation of the real damping characteristics of the soil.

hardening small strain model; Rayleigh damping; Rayleigh wave; seismic dynamic response; finite element dynamic analysis

2016-04-13 基金项目：福建省自然科学基金资助项目(2016J01271);福建省住房和城乡建设厅科学技术项目(2015-K-38);福建省住房和城乡建设厅科学技术项目(2016-K-26)

施有志(1976-),男,福建晋江人,博士,副教授,主要从事岩土工程、地下工程等领域的教学与科研工作。 E-mail:2013110907@xmut.edu.cn。

TU435

A

1000-0844(2016)06-0896-07

10.3969/j.issn.1000-0844.2016.06.0896