在“思维流程图”的构建中挖掘“突变因子”
2017-01-13王涛
王 涛
(江苏省南京东山外国语学校,江苏 南京 211103)
在“思维流程图”的构建中挖掘“突变因子”
王 涛
(江苏省南京东山外国语学校,江苏 南京 211103)
在解决问题的过程中,严密的逻辑思维彰显了物理学科的特点,体现了学科的魅力.在物理问题的分析中我们需要经历总结、提炼、归纳、概括,进而通过思维加工形成分析某类问题研究的思维图景,并通过“思维流程图”的构建加以呈现,本文以动力学中突变问题分析为例,予以说明.
动力学;思维流程图;思维方法;突变因子
重视科学方法的教学对学生核心素养的培养是至关重要的,物理严密的逻辑思维彰显了物理学科的特点,体现了学科的魅力所在.在物理问题的分析讨论中,我们需要经历总结、提炼、归纳、概括,进而通过思维加工形成分析某类问题研究的思维图景,并通过“思维流程图”的构建加以呈现,笔者以动力学中“突变问题”为例,在“思维流程图”的构建中挖掘其“突变因子”,帮助学生分析、解决问题,培养学生的思维能力,优化学生的思维品质.
1 叠加体模型的突变性问题分析
问题呈现:如图1所示,质量M=2.0kg的长木板A放在光滑水平面上,质量m=0.5kg的小滑块B放在长木板A的最右端,滑块与长木板间的动摩擦因数μ=0.3,设最大静摩擦力与滑动摩擦力相等,问:F为多大时A、B可保持相对静止?F为多大时A、B会发生相对滑动?
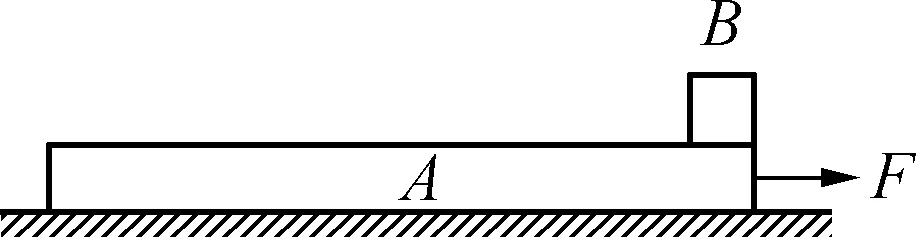
图1
分析:对于此类问题,教师往往通过对临界情况的分析,即当A、B恰好能保持相对静止的情况作为问题的突破口,把相对静止和相对运动两类情况分开.然而从教学实践来看,学生对临界情况的认识是模糊的,对力和运动的关系没有形成整体性把握,从相对静止到相对运动的突变性问题成了学生理解的难点,也成了教师教学的难点.
仔细研究学生的“难”和教师的“难”可以发现,对问题认识不清的主要症结在于A、B从“相对静止”过渡到“相对运动”的思维链条出现了断裂.这就需要教师把连续变化的思维过程加以澄清,让学生对问题的分析有一个更加清晰的思路和整体性的把握.
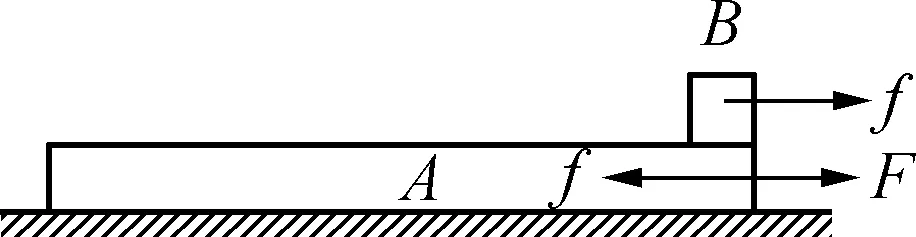
图2
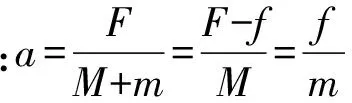
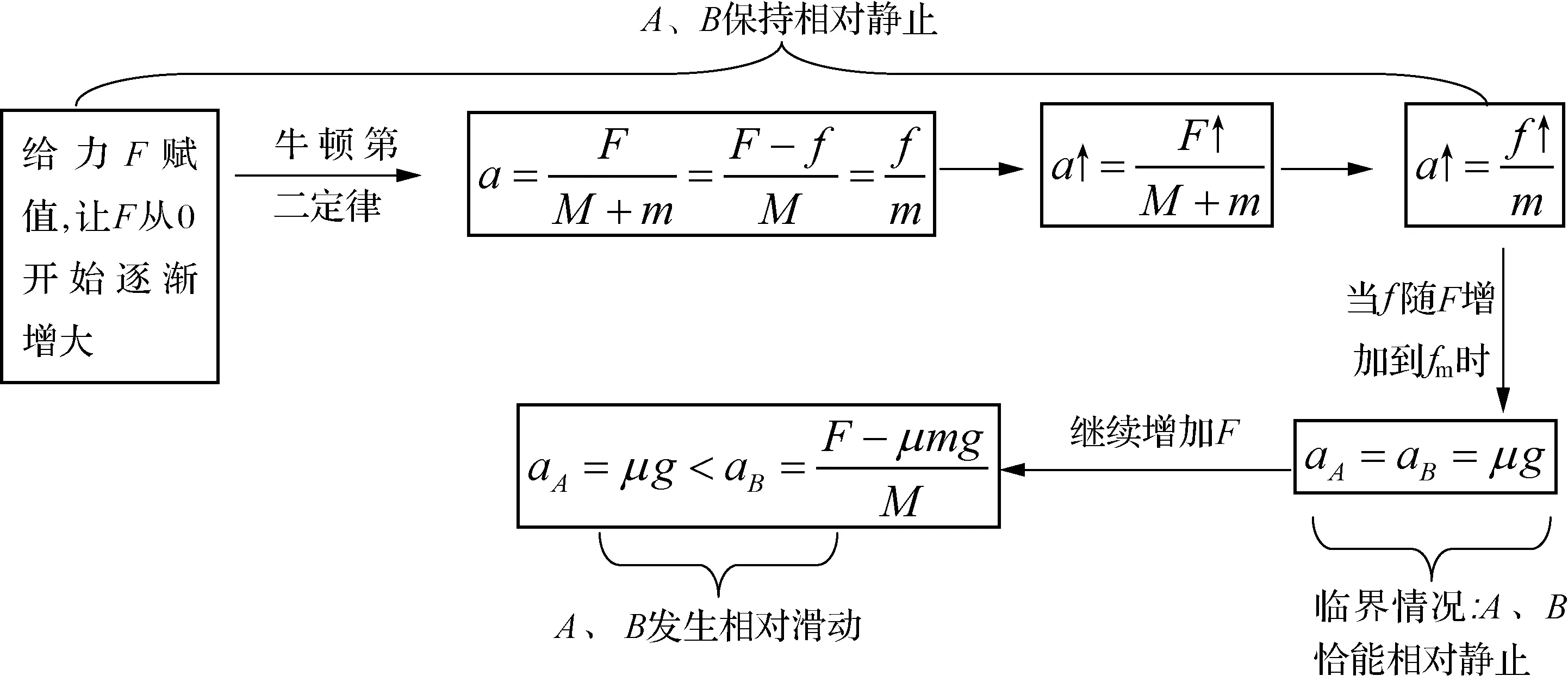
图3
由以上思维流程图可以看出,临界情况是发生突变(由相对静止到相对滑动)的过渡,是力F渐变过程中的某一瞬时的状态,然而我们的思维不能仅仅停留在该状态的讨论,而应该从F渐变的连续性角度展开思考,让力和相对运动关系的思维脉络具有连贯性.思维流程图是从力的角度出发来推知运动情况的变化,而在思维流程图的构建中“突变因子”(临界态)被显化.从问题的解决效果上来看,这样的逻辑推理不仅把模糊的难点问题化解在F“渐变”式的讨论中,同时学生更易于把握力和运动之间的关系以及相对运动变化的原委.
2 传送带模型的突变性问题分析
问题呈现:如图4所示,传送带与地面倾角为θ,AB长为L(足够长),传送带以v的速率逆时针转动,在传送带上端A无初速的放一质量为m物体,它与传送带间的动摩擦因数为μ,设最大静摩擦力与滑动摩擦力相等,试分析讨论物体从A到B做何运动?
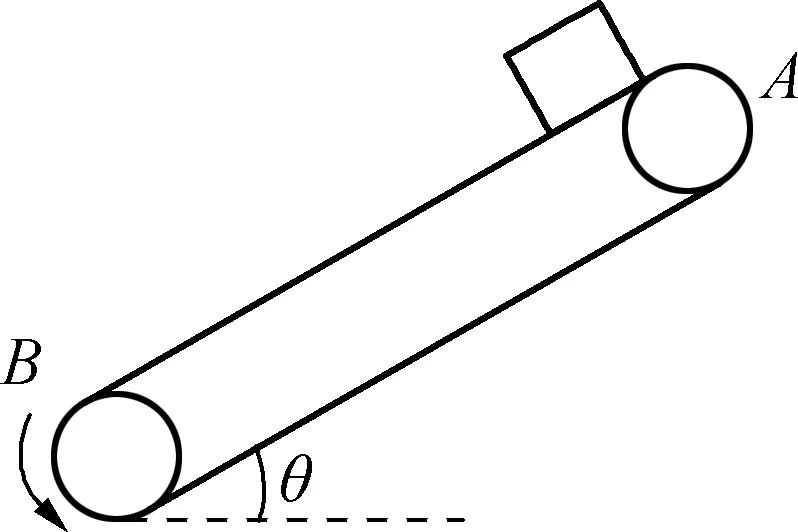
图4
分析:此类问题的难点在于当物块在传送带上加速达到与传动带等速后的受力分析和运动分析.从教学实践中来看,学生的主要问题出现在等速这一状态(时刻)下摩擦力的识别与判断模糊不清,从而造成对等速后的运动状态认识不清.
摩擦力的被动性特征是造成疑难的最根本原因,尤其是在滑块与传送带相对运动过程中达到等速这一瞬时状态下的分析,更是增加了问题分析的思维难度.这就需要教师在此“突变”环节中精雕细琢,以合乎逻辑的推理加以辨析、判断.
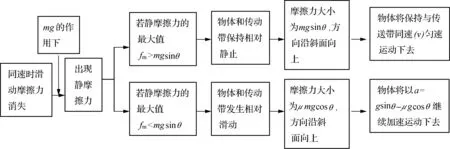
在物体从静止加速运动的过程中,受到的摩擦力如图5所示,当在C位置与传送带等速时,此时滑动摩擦力f1消失.因为重力的存在使得物体相对于传送带具有向下的滑动趋势,所以此时应出现静摩擦力f2.这个静摩擦力能否足够大,维持物体和传送带一同匀速运动下去呢?这就需要比较最大静摩擦力fm与mgsinθ的大小关系.
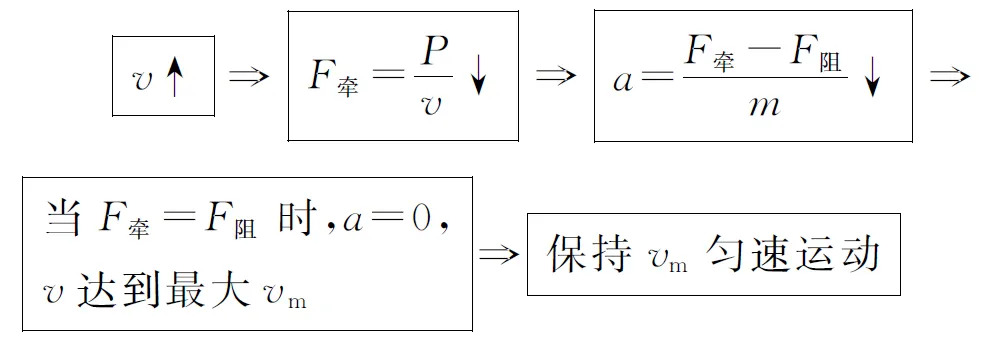
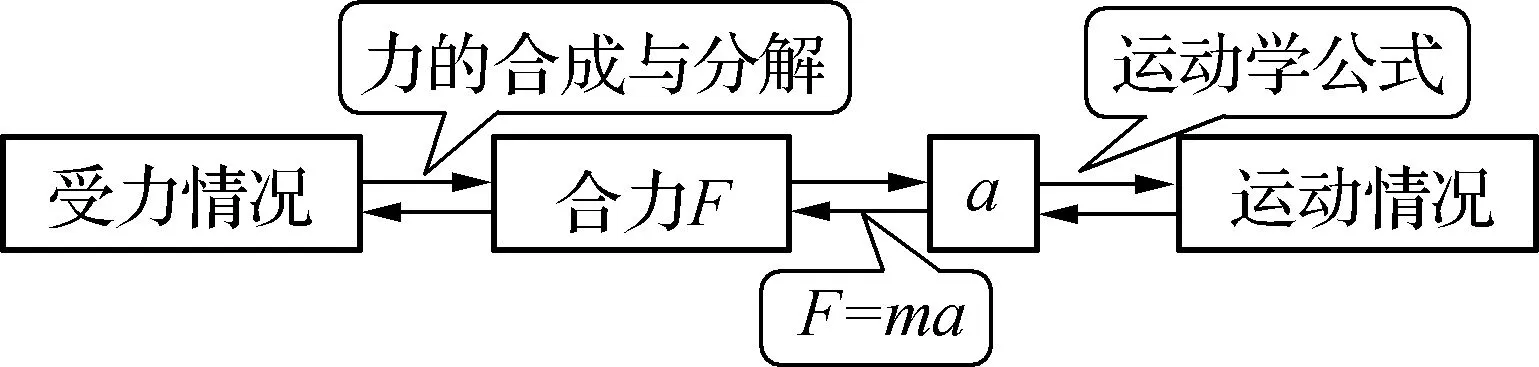
若fm>mgsinθ,则物体与传动带保持相对静止一同匀速,此时的静摩擦力大小等于mgsinθ,方向沿斜面向上,与f1反向(如图6);若fm 图7 静摩擦力f2在上述分析中以一种假设的方式呈现,并利用其最大值fm与mgsinθ的比较作为运动判断的依据,其思维流程可以用图8说明. 图8 由图8思维流程图可以清晰地看出,突变的状态发生在等速这一瞬时,讨论的依据在于假设静摩擦力的存在,分析聚焦于比较fm与mgsinθ的大小关系,突变因子在讨论、分析中得以显现,运动图景清晰可见. 思维流程图源于计算机语言中的流程图,是用简单的字母或文字符号表示的推理思路、步骤、因果联系,最后得出结果的思维过程示意图.学生在较复杂物理问题面前往往束手无策,而思维流程图采用“一因一果”的渐进式推理,能够帮助学生形成正确的思维方法,从而提高学习效率. 从以上两类问题的分析可以看出,利用思维流程图可以更为直观地显示思维过程,更易于学生从整体上把握突变状态的发生,也易于学生深度理解“突变”的原委,为该类问题的分析提供了切实可行的思维方法. 其实在高中物理学习中这样分析问题的思路是常见的,比如在机车以恒定功率P启动的问题中就是通过思维流程图展开分析、讨论(如图9). 图9 另外,利用牛顿运动定律解决动力学问题的思路也可以用简洁明快的思维流程图予以呈现(如图10). 图10 从实践的效果来看,思维流程图直观和严谨的逻辑推理大大降低了问题分析的难度,采用的因果联系的渐进式推理,强调物理意识及思维途径,细化推理阶梯,对培养学生物理思维能力、提升学生思维品质大有裨益! [1] 邢红军.高中物理科学方法教育[M].北京:中国科技出版社,2015.8. [2] 司国民.用思维流程图帮你提高思维能力[J].物理教学探讨,2006,(2). [3] 耿玉盛.传送带模型中摩擦力的突变问题探讨[J].物理之友,2016,32(2). [4] 赵生武.关于倾斜传送带上物体运动可能性的探讨[J].物理之友,2016,32(4). [5] 胡平.理想模型的建立过程——以课堂教学“牛顿运动定律的应用——瞬时性问题”为例[J].物理之友,2014,30(12). [6] 潘利敏,殷绍燕.板块模型的特征与解决策略[J].物理之友,2016,32(9).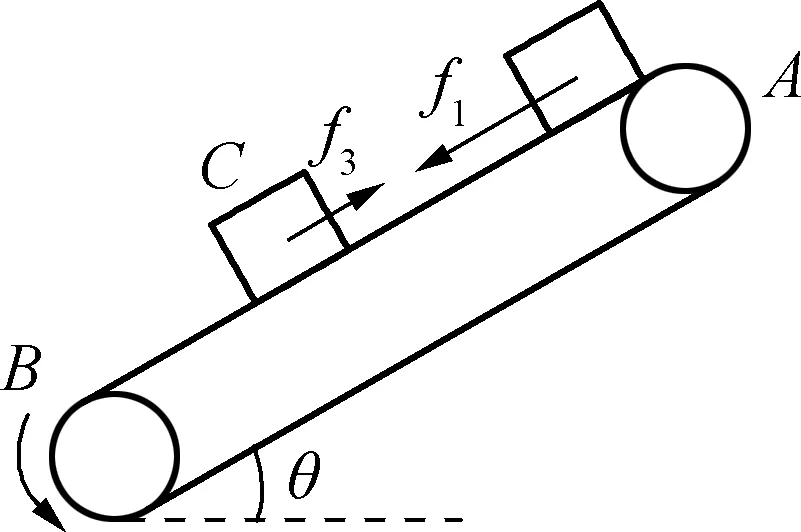
3 启示