一个在Armijio线搜索下全局收敛的改进共轭梯度法
2017-01-13吴素花
吴素花
(重庆师范大学 数学科学学院,重庆 401331)
一个在Armijio线搜索下全局收敛的改进共轭梯度法
吴素花
(重庆师范大学 数学科学学院,重庆 401331)
非线性共轭梯度方法是解大规模无约束问题最有效的方法之一,改进了Liu等人提出的共轭梯度算法得到MD方法,MD方法不依赖任何线搜索具有充分下降性.在Armijio型非精确线搜索下, 证明了新方法的全局收敛性.
无约束优化问题;共轭梯度法;Armijio线搜索;充分下降性;全局收敛性
本文主要考虑以下无约束极小问题:
minf(x),x∈Rn
(1)
共轭梯度法是求解这类问题的最有效的方法之一, 其一般迭代格式为:
xk+1=xk+αkdk
(2)
(3)
其中:αk由某种线搜索确定的步长,gk表示f(x)在点xk处的梯度,参数βk称为共轭梯度参数.本文中涉及的线搜索有下列两种:

(4)
标准沃尔夫线搜索:
(5)
其中 0<δ<σ<1. 若存在常数c>0下式成立,则称方法具有充分下降性.
参数βk的不同取法对应于不同的共轭梯度法,经典的共轭梯度法有HS方法、FR方法、LS方法、CD方法、DY方法,具体的βk选取见文献[1-8].其中PRP方法、HS方法、 LS方法的计算效果比较好, 但是理论比较差;而FR方法、CD方法、DY方法的计算效果比较差,但是理论好.为了寻求在理论及数值计算上都比较好的方法,许多学者对共轭梯度方法进行了研究.
2005年,Hager和Zhang[9]提出了HZ方法,其中参数βk的选取如下:
(6)
其中:yk-1=gk-gk-1,sk-1=xk-xk-1.
Dai 和 Kou[10]提出了DK方法,其中参数βk的选取如下:
(7)
2015年,Liu[10]提出D方法,共轭梯度参数βk如下:
(8)
为了得到方法对一般函数的全局收敛性,文中对D方法进行了如下的截断修正:

1 方法的提出
下面分析liu等[11]提出的D方法.D方法的共轭梯度参数如下:
令:


Dai[12]提出了修正割线条件:Bksk-1=zk-1
(9)

用割线条件式(9)对D方法进行修正得到MD方法,共轭参数βk取值如下:
(10)

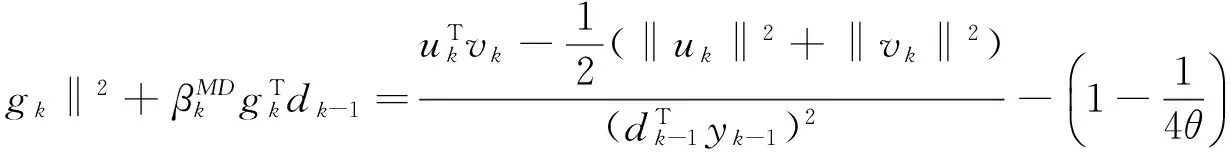

下证MD方法的全局收敛定理.
2 收敛性分析
为了证明MD方法的全局收敛性, 对目标函数进行一般假设:
(A2) f(x)在水平集Ω的一个领域N内连续可微,并且梯度gk满足Lipschitz连续,即存在常数L>0使得下式成立:
‖g(x)-g(y)‖≤L‖x-y‖,∀x,y∈N .
(11)
为了证明MD方法的全局收敛性,分三步进行:首先证明MD方法不依赖线搜索具有充分下降性;然后给出两个引理;最后证明全局收敛定理.

(12)
证明该定理由第二部分方法的提出过程易证得.
引理1αk>0由Armijo线搜索(4),则存在一个常数c1>0,使得下式对所有k≥0都成立:
(13)
证明由Armijo线搜索以及假设(A1)-(A2)可得:

(14)
下面分两种情况证明式(13):

2)当αk<1时,由Armijio线搜索条件可知ρ-1αk不满足式(4),则有下式成立:
(15)
由微分中值定理以及Lipschitz条件(11)式,存在t∈(0,1)使得:
‖xk+tρ-1αkdk-xk‖‖dk‖

引理2假设(A1)~(A2)成立,αk>0由Armijo线搜索求得,βk由式(10)确立,dk由式(3)确定,则有:

(16)
证明由式(13)和式(14)可得:

由式(12)可得:

(17)
证毕.
下证MD方法对一般函数的全局收敛性.
定理2目标函数f(x)满足一般假设(A1)~(A2),αk由Armijo线搜索确定 ,MD方法全局收敛,即:

(18)
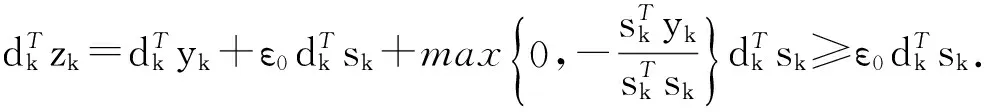

由上式及式(3)可得:

[1]HESTENESMR,STIEFELE.Methodsofconjugategradientsforsolvinglinearsystems[J].JournalofResearchoftheNationalBareauofStandards,1952,49:409-436.
[2]FLETCHERR,REEVESCM.Functionminimizationbyconjugategradients[J].TheComputerJournal,1964,7(2):149-154.
[3]POLAKE,RIBIEREG.Notesurlaconvergencedeméthodesdedirectionsconjuguées[J].ESAIM:MathematicalModellingandNumericalAnalysis-ModélisationMathématiqueetAnalyseNumérique,1969,3(R1):35-43.
[4]POLYAKBT.Theconjugategradientmethodinextremalproblems[J].USSRComputationalMathematicsandMathematicalPhysics,1969,9(4):94-112.
[5]FLETCHERR.PracticalMethodsofOptimizationvol.1:UnconstrainedOptimization[M].NewYork:JohnWiley&Sons,1987.
[6]LIUY,STOREYC.Efficientgeneralizedconjugategradientalgorithms,Part1:Theory[J].JournalofOptimizationTheoryandApplications,1991,69(1):129-137.
[7]DAIYH,YUANGY.Anonlinearconjugategradientmethodwithastrongglobalconvergenceproperty[J].SIAMJournalonOptimization,1999,10(1):177-182.
[8] 王胜,关洪波.一种求解单调非线性方程组的凸组合算法[J].吉首大学学报(自然科学版),2014,35(1);12-14.
[9]HAGERWW,ZHANGH.Anewconjugategradientmethodwithguaranteeddescentandanefficientlinesearch[J].SIAMJournalonOptimization,2005,16(1) :170-192.
[10]DAIYH,KOUCX.AnonlinearconjugategradientalgorithmwithanoptimalpropertyandanimprovedWolfelinesearch[J].SIAMJournalonOptimization,2013,23(1):296-320.
[11]LIUH,WANGH,QIANX,etal.Aconjugategradientmethodwithsufficientdescentproperty[J].NumericalAlgorithms,2015,70(2):269-286.
[12]DAI,ZF,FENGHW.Globalconvergenceofamodifiedhestenes-stiefelnonlinearconjugategradientmethodwitharmijolinesearch[J].NumericalAlgorithms,2012,59(1):79-93.
责任编辑:时 凌
An Improved Conjugate Gradient Method with Global Convergence Property Under the Armijio Line Search
WU Suhua
(School of Mathematics Science,Chongqing Normal University,Chongqing 401331,China)
Conjugate gradient methods are a class of important methods for solving large-scale unconstrained optimization problems.In this paper,we present a modified conjugate gradient method based on the conjugate gradient parameter of Liu et al..The new method has sufficient descent property independent of any line search.We establish the convergence results of the algorithms under the Armijio line search conditions.
unconstrained optimization;conjugate gradient method;Armijio line search;suffcient descent property;global convergence
2016-07-16.
吴素花(1991- ),女(苗族),硕士生,主要从事最优化理论和算法研究.
1008-8423(2016)04-0394-04
10.13501/j.cnki.42-1569/n.2016.12.008
O224
A
