关于亚交换群的对合交换图

谭延庆，沈如林

(湖北民族学院 理学院，湖北 恩施 445000)



关于亚交换群的对合交换图

谭延庆，沈如林

(湖北民族学院 理学院，湖北 恩施 445000)

对合交换图是以群中2阶元共轭类为顶点，两顶点有边当且仅当它们交换的图.讨论了亚交换群的对合交换图结构.

对合交换图；群扩张；亚交换群

1 引言及结果

设G是有限群，且X为G的一个二阶共轭类，X在G中的对合交换图ΓG(X)是指以X中元为顶点，互异点x,y∈X有一条边当且仅当xy=yx.称图ΓG(X)为正则图，如果ΓG(X)中每个顶点所连的边数都相同.如果正则图中每个顶点相连的边数为k，则称为k-正则图.特别，0-正则图称孤立点图.文献[1-6]中分别研究了G为散在单群、有限Coxeter群、对称群及特殊线性群时对合交换图ΓG(X)的结构，文献[7]讨论了亚循环2-群对合交换图的结构.本文讨论了亚交换群对合交换图的结构.所谓亚交换群即交换群被交换群的扩张.设A,B都是交换群，映射φ：B→Aut(A)为群同态，函数f:B×B→A，满足：

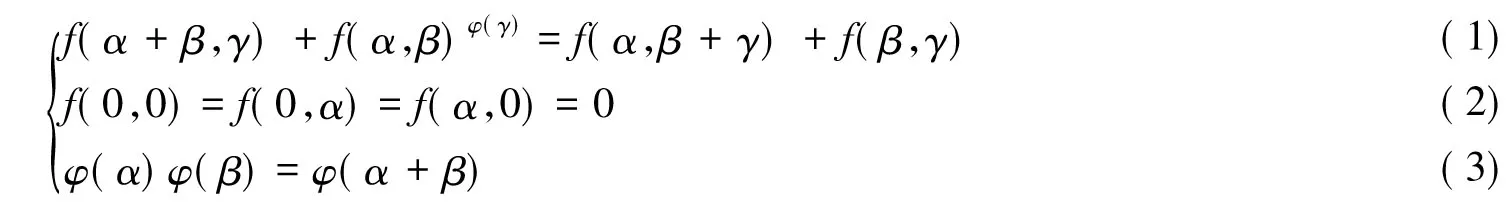
这里∀α,β,γ∈B，规定G为集合(B,A)，并且在G中定义乘法：

(α,a)(β,b)=(α+β,f(α,β)+aφ(β)+b)，∀(α,a),(β,b)∈G.

则G是交换群A被交换群B的扩张[8]，记G=Ext(A,B;f,φ).本文中证明了：

定理1设A,B均是交换群，G=Ext(A,B;f,φ)，并设(α,a)为G中任意二阶元，取A的子群H={-b+bφ(α)|b∈A}，则(α,a)的共轭类在G中的对合交换图是(r-1)-正则的，r为所有陪集H+f(β,α)-f(α,β)+a-aφ(β)中二阶元的个数之和，β取遍B中所有元.

2 定理1的证明

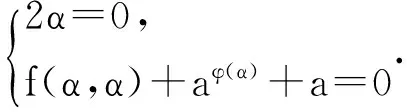
任意取(β,b)∈G，结合上面的(1)式，有：(α,a)(β,b)=(α,f(α,β)-f(β,α)+aφ(β)-bφ(α)+b)，则二阶元(α,a)的共轭类可表示为(α,a)G={(α,f(α,β)-f(β,α)+aφ(β)-bφ(α)+b)|β∈B,b∈A}.

另外，若(β,b)∈CG(α,a)，则：(α,a)(β,b)=(α,f(α,β)-f(β,α)+aφ(β)-bφ(α)+b)=(α,a)，即(α,a)的中心化子CG(α,a)={(γ,c)|γ∈B,c∈A,且f(α,γ)-f(γ,α)+aφ(γ)-cφ(α)+c=a}.

考虑二阶元(α,a)的中心化子与其共轭类的交.由上述计算得到：

(α,a)G∩CG(α,a)={(α,c)|b,c∈A,β∈B,c=f(α,β)-f(β,α)+aφ(β)-bφ(α)+b，且(a-c)φ(α)=a-c}.

令集合H={-b+bφ(α)|b∈A}，H是A的子群.(α,a)为G中取定二阶元，交(α,a)G∩CG(α,a)中的元等价于陪集H+f(β,α)-f(α,β)+a-aφ(β)中的二阶元，即(α,c)∈(α,a)G∩CG(α,a)⇔2(a-f(α,β)+f(β,α)-aφ(β)+bφ(α)-b)=0.这是因为由前面的式(1)可得：

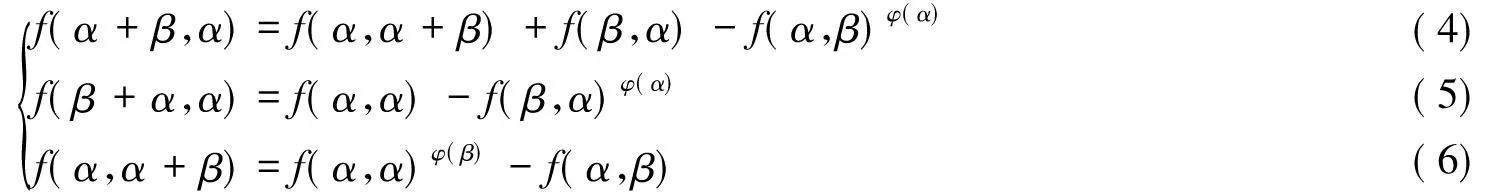
∀α,β∈B.联立式(4)～(6)可得：

(f(α,β)-f(β,α))φ(α)=f(β,α)-f(α,β)+f(α,α)φ(β)-f(α,α)

(7)

因为c=f(α,β)-f(β,α)+aφ(β)-bφ(α)+b，陪集H+f(β,α)-f(α,β)+a-aφ(β)中二阶元满足2(a-f(α,β)+f(β,α)-aφ(β)+bφ(α)-b)=0，即2(a-c)=0，也即a-c=c-a⇔(a-c)φ(α)=(a-f(α,β)+f(β,α)-aφ(β)+bφ(α)-b)φ(α)=(f(β,α)-f(α,β))φ(α)+aφ(α)-aφ(α+β)-bφ(α)+b=(f(β,α)-f(α,β))φ(α)-f(α,α)-a+f(α,α)φ(β)+aφ(β)-bφ(α)+b((α,a)二阶元)=f(α,β)-f(β,α)-a+aφ(β)-bφ(α)+b(代入式(7))=c-a=a-c.定理1得证.

3 特殊的亚交换群

由定理1，要求交换群对交换群扩张的对合交换图，还需要解决交换群的自同构群问题.文献[9-10]给出了求有限交换p群的自同构群的方法.具体内容如下：

进一步，文献[10]也给出了一般有限p群的自同构群.设有限交换p群A的型为：

其中m1>m2>…>mt≥1,Si>0.又设矩阵：

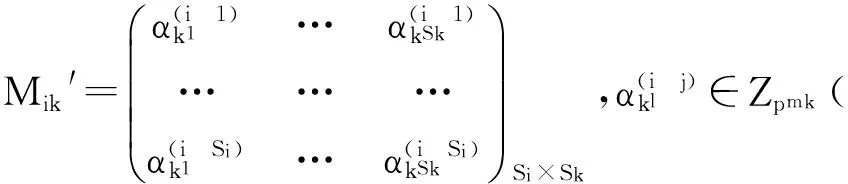
例1若取A=Z8×Z2，B=Z2×Z2，G=Ext(A,B;f,φ)，则G中对合交换图为1-正则、2-正则和孤立点图.

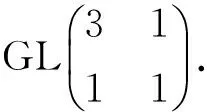
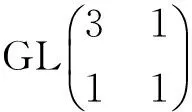
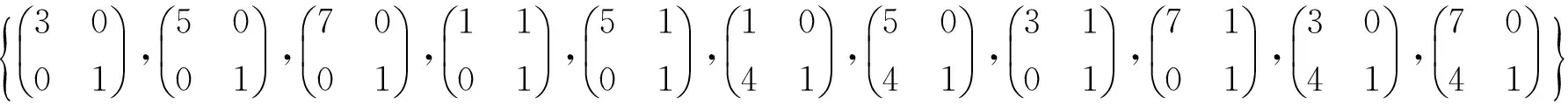
故A有11个二阶子群,且其与群Z2×Z2同构的子群有：

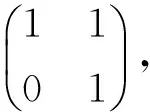
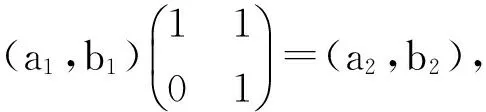
为便于讨论，以下用表格来展示陪集H+f(β,α)-f(α,β)+a-aφ(β)中二阶元的情况及对合交换图的结构，这里H={-b+bφ(α)|b∈A}.α固定，不妨设f(β,α)-f(α,β)=δ(x,y).由于f:B×B→A，因此可令δ(x,y)=(x,y)∈A.对于每个二阶元(α,a)，φ(β)取遍所有φ(B)的值.

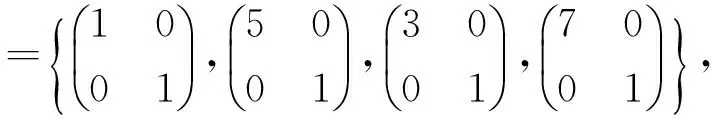
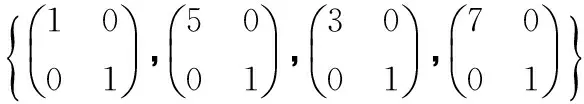
表1 φ(B)取时G中对合交换图的结构Tab.1 The structure of the commuting involution graph of

续表1：

φ(α)Ha-aφ(β)f(α,α)δ(x,y)G中对合交换图结构5001()(0,0)(4,0)同上(2a0,0)(6x,0)=(-6a0,0)+(6a0,0)φ(β)⇒(6x,0)=(0,0)或(4a0,0)(0,0),(0,1),(4,0),(4,1),或6x≡4a0(mod8).同上3001()(0,0)(2,0)(4,0)(6,0)同上(4a0,0)(4x,0)=(-4a0,0)+(4a0,0)φ(β)⇒(4x,0)=(0,0)(0,0),(0,1),(2,0),(2,1),(4,0),(4,1),(6,0),(6,1)同上7001()(0,0)(2,0)(4,0)(6,0)同上(0,0)(0,0)=(0,0)恒成立.(x,y),x=0,1,…,7,y=0,1.同上

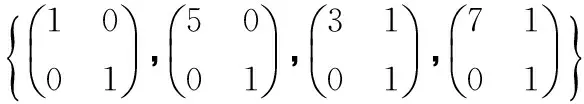
表2 φ(B)取时G中对合交换图的结构Tab.2 The structure of the commuting involution graph of

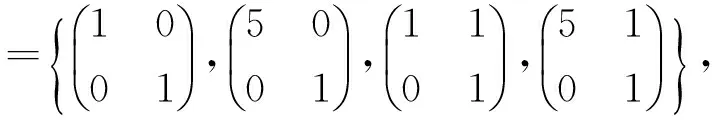
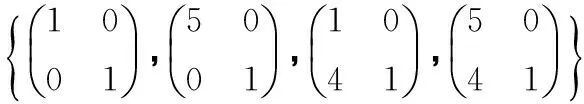
表4 φ(B)取时G中对合交换图的结构Tab.4 The structure of the commuting involution graph of

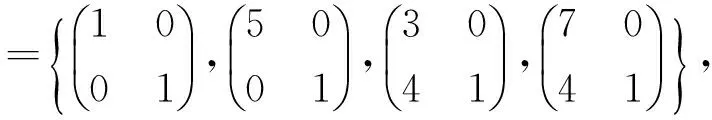
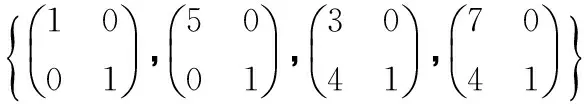
表5 φ(B)取时G中对合交换图的结构Tab.5 The structure of the commuting involution graph of

同理，当φ(B)取二阶群时，陪集H+f(β,α)-f(α,β)+a-aφ(β)可以取到(0,1),(4,0),(4,1)三个中的一个、两个、或三个.

综上所述，G中对合交换图为1-正则、2-正则和孤立点图.证毕.

问题亚交换群对合交换图中每个顶点所对的边数是否有上界？

[1]BATES，BUNDYC，PERKINSD,etal.CommutinginvolutiongraphsforfiniteCoxetergroups[J].JournalofGroupTheory,2014,6(4):461-476.

[2]GHOLAMINEZHADF.StructuresandTopologicalIndicesofCommuttingInvolutionGraphs[J].ElectronicNotesinDiscreteMathematics,2014,45(45):187-194.

[3]BATESC,BUNDYD,HARTS,etal.Commutinginvolutiongraphsforsporadicsimplegroups[J].JAlgebra,2007,316(2):849-868.

[4]BATESC,BUNDYD,PERKINSS,etal.CommutinginvolutiongraphsforfiniteCoxetergroups[J].JGroupTheory,2003,6(4):461-476.

[5]BATESC,BUNDYD,PERKINSS.etal.Commutinginvolutiongraphsforsymmetricgroups[J].JAlgebra,2003,266(1):133-153.

[6]BATESC,BUNDYD,PERKINSS.etal.Commutinginvolutiongraphsinspeciallineargroups[J].CommAlgebra,2004,32(11):4179-4196.

[7] 谭延庆,沈如林.关于亚循环2-群的对合交换图[J].湖北民族学院学报(自然科学版),2016,34(1):20-23.

[8] 徐明曜.有限群导引(上)[M].北京：科学出版社，1999.

[9] 俞曙霞.有限交换p群的自同构群[J].广西大学学报(自然科学版),1983(2):90-95.

[10] 华罗庚. 典型群[M].上海：上海科学技术出版社,1963.

责任编辑：时 凌

On Commuting Involution Graphs of Metabelian Groups

TAN Yanqing，SHEN Rulin

(School of Science,Hubei University for Nationalities,Enshi 445000,China)

For a group G and a conjugacy classXof an involution ofG,the commuting graphΓG(X) of G onX,is the graph whose vertex set isXand distinct verticesxandyhaving an edge if and only ifxy=yx. In this paper, we discuss the structure of the commuting involution graph of metabelian groups.

commuting involution graph;group extension;metabelian group

2016-11-02.

国家自然科学基金地区项目(11201133).

沈如林(1977- )，男，博士，副教授，主要从事有限群及代数编码的研究.

1008-8423(2016)04-0371-05

10.13501/j.cnki.42-1569/n.2016.12.003

O152

A

作者简介：谭延庆(1990- )，男(土家族)，硕士生，主要从事群论的研究；*