基于并行分层时间间隔测量的TDOA定位算法研究

邹东尧，刘碧微，杨 威，向家钰

(1.郑州轻工业学院 计算机与通信工程学院，河南 郑州 450001;2.中国科学技术大学 数学科学学院，安徽 合肥 230026)



基于并行分层时间间隔测量的TDOA定位算法研究

邹东尧1，刘碧微1，杨 威1，向家钰2

(1.郑州轻工业学院 计算机与通信工程学院，河南 郑州 450001;2.中国科学技术大学 数学科学学院，安徽 合肥 230026)

基于到达时间差(TDOA)定位算法要求精确地时间同步技术作为支撑.由于传统时间同步技术精度低导致TDOA定位结果有偏差，提出一种基于并行分层次时间间隔测量的到达时间差(TDOA)和到达信号增益比(GROA)联合定位算法.基于TDOA与GROA联合定位模型，构造含拉格朗日系数的优化函数，然后采用约束加权最小二乘算法(TSWLS)来进行求解；同时，采用并行分层时间间隔测量法来控制定位算法的时间同步.实验分析表明，该算法相比较传统的TDOA定位算法而言，定位精度提高了25 dB，并且具有相对较高和较稳定的定位精度.

时间同步；到达时间差(TDOA)；到达信号增益比(GROA)；最小二乘；并行分层测量

节点定位在整个传感器网络中占有重要的地位，在事件观测、目标跟踪、网络重构等方面都是不可缺少的环节[1-2].一般常见的无源定位方法是利用诸如到达时间(time of arrival,TOA)、到达时间差(time difference of arrival，TDOA)、波达角(angle of arrival，AOA)等测量参数或者它们的组合来实现目标的定位.常用的基于接收信号能域信息的定位方法有接收信号强度定位方法RSSI(Receive Signal Strength Indicator)[3-5]和到达信号增益比定位方法GROA(Gain Ratio of Arrival)[6-8].TDOA定位技术是利用发射端发射信号与接收端接收信号的时间差进行测距，所以要求有精确地同步时钟.时间同步是指两频率信号之间的时间差被消除或被最小化处理，并且处理后的时间差值不会随时间的变化而变化.高进度的时间同步不仅在地球动力学、脉冲周期、相对论以及人造卫星动力学测地等基础研究方面有着重要的作用，而且在航空航天、导航定位卫星发射等领域也具有极其重要的地位[9-10].时间同步离不开短时间间隔的测量，然而传统的时间间隔测量方法存在测量范围宽，但是测量精度不高的问题.RSSI定位技术因符合低功率、低成本的要求在多传感器网络节点定位中应用广泛，但这些条件在无源定位中是不满足的，所以RSSI定位方法在被动定位中无法适用.GROA定位不需要事先已知待定位目标的信号发射功率和信号传播的路径损耗模型，仅利用目标信号在自由空间传播时，接收站接收到目标信号的幅度与传播距离成反比[6]的原理来对目标进行定位，更适用于无源定位.

GROA的定位方法首先由K.C.Ho等人在文献[6]中提出.他们提出同时利用GROA和TDOA测量信息的两步加权最小二乘(two step weighted least square，TSWLS)无源定位方法，并且文献[6]指出在这种混合体制的定位方法中，随着信号带宽的减小，GROA对定位精度的改善起到了关键的作用.在此基础上文献[7]提出了在传感器位置有误差条件下的TDOA和GROA多信号源两步加权最小二乘被动定位方法，并指出利用GROA定位信息需要精确测量出所使用环境的传播系数.文献[8]在文献[7]的基础上，给出了BiasRed法与BiasSub法两种偏差消减算法来进一步提升TDOA和GROA联合定位精度.

因此，本文主要考虑接收传感器存在位置误差以及定位结果易受干扰的问题，联合时域TDOA定位信息与能量域GROA定位信息，对信号源进行协同定位.同时TDOA与GROA定位要求精确地时间同步，本文提出一种基于并行时间间隔的时间同步测量，最后采用优化粒子群算法计算定位最优值.首先，基于TDOA与GROA定位模型提出了含有拉格朗日系数的优化函数，采用约束加权最小二乘算法来进行迭代求解；同时，利用并行分层时间间隔测量法来确保TDOA与GROA定位的时间同步；最后通过计算机仿真验证本文算法在不同的参数条件下的定位效果，实验结果均表明，本文提出的算法相比TDOA算法鲁棒性好，定位精度高.

1 TDOA与GROA定位方法

1.1 TDOA定义

接收传感器收到的信号源发射的信号定义为：

(1)

其中i=2,3,…，M.s(t)表示目标发射信号，ξi(t)表示第i个接收传感器的信号接收噪声，xi(t)为第i个接收传感器接收到的信号.不失一般性，以第一个接收传感器作为参考节点.

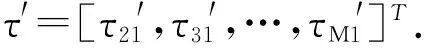
将时差值乘以信号传播速度c得到目标到第i个传感器和到传感器1的到达距离差(RDOA).则第i个传感器与目标之间的距离可以表示为：

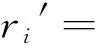
(2)

其中‖*‖表示欧氏距离，i=2,3,…，M，则目标到第i个传感器和第1个传感器之间的距离差为：

(3)

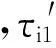
r=r′+Δr

(4)

假设时差误差满足零均值高斯分布，其协方差矩阵为E[ΔrΔrT]=Qr.

1.2 GROA定义

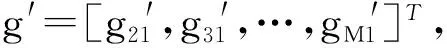
(5)

为方便表示，GROA参数可写为向量形式：g=[g21,g31,…,gM1]T，Δg=[Δg21,Δg31,…,ΔgM1]T.进一步，到达增益比测量方程：

g=g′+Δg

(6)

其中：gi1为实际GROA测量值，Δgi1为GROA测量误差值.假设其满足零均值高斯分布，并独立于时差测量误差，其协方差矩阵为E[ΔgΔgT]=Qg.

2 基于并行分层时间间隔测量的TDOA和GROA定位方法

本文主要研究基于时差(TDOA)和增益比(GROA)联合的定位问题.已知定位方程与目标位置之间的非线性关系，那么实现目标位置的直接求解难度较大.目前针对这一非线性方程求解问题主要有两大类方法：一是泰勒级数展开方法[11]，即通过在目标真实位置附近将非线性方程进行泰勒级数展开，并舍去二阶以上高次项，得到线性方程，并通过多次迭代逼近目标的真实位置；二是通过引入辅助变量[12]，将非线性方程伪线性化，再求解伪线性方程获得目标的位置信息.第一类方法往往要求一个较为精确的迭代初始值，并不能够保证完全收敛到真实位置处.第二类方法在一定条件下具有闭式解，且不存在发散问题.典型的算法有两步加权最小二乘(two-step weighted least-squares，TSWLS)算法[13]、约束加权最小二乘(constrained weighted least squares，CWLS)算法[14]等，其中，TSWLS算法运算量最小，CWLS、CTLS算法利用最小二乘(least squares，LS)解作为初始解，在利用迭代算法获得目标位置.

本文利用以上思想，本文提出了基于TDOA与GROA联合定位算法，并采用基于并行分层时间间隔测量的方法来确保高精度的定位时间同步，最后采用优化粒子群算法计算最优值.利用Matlab仿真工具，通过与传统的TDOA定位算法相比较，来验证本文算法的性能.

图1 TDOA和GROA联合定位示意图Fig.1 The localization layout of TDOA and GROA

2.1 定位场景分布

图1为基于接收传感器时差测量值(TDOA)和接收信号到达增益比(GROA)联合定位示意图.

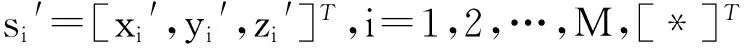
2.2 建立定位方程

(7)

将式(2)带入式(7)并两边平方，可以得到：

(8)

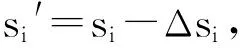
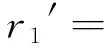
(9)

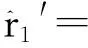
(10)

(11)

(12)

通过从1989年～2011年，2012年～2017年两个不同时段对我国信息素养主题研究论文进行统计分析，特别是近6年来的研究现状，可以发现以下几点。

(13)

由式(13)及式(9)可以得到:

(14)

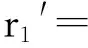
(15)

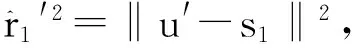
(16)

(17)

其中：

(18)

根据误差关系可得：

εt=B11Δr+C11Δg+D11Δβ

(19)

(20)

(21)

其中，O为3×1维全零向量.

同理，记εg=[εg,2,εg,3,…,εg,M]T，则:

(22)

其中：

(23)

根据误差关系可得：

εg=B12Δr+C12Δg+D12Δβ

(24)

(25)

(26)

其中：I(M-1)×(M-1)为M-1维单位矩阵，0为3×1维全零向量.

由于测量误差、站址误差的存在，TDOA、GROA参数测量结果存在误差，式(17)、(24)不为0.

(27)

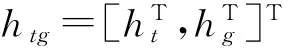
(28)

又知:

εtg=BtgΔr+CtgΔg+DtgΔβ

(29)

(30)

构造最小化目标函数:

(31)

其中W为加权矩阵:

(32)

则:

(33)

引入式(15)的约束条件，求解目标位置即为在满足式(31)和式(15)的约束条件下，求解目标位置u，使得εtg的范数平方最小化，数学上可表示为:

(34)

首先利用u′Tu′=(a+h)2，可以得到引入约束信息的最小化目标函数:

(35)

其中λ1、λ2为拉格朗日(Lagrange)系数.式(35)中L(u,λ1,λ2)即为所构造的优化函数.

2.3 求解拉格朗日系数

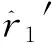
(36)

(37)

(38)

(39)

(40)

(41)

将式(41)带入式(36)可得:

(42)

将式(41)和式(42)带入式(40)可得:

(43)

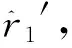
2.4 优化粒子群算法算法

为确保定位算法的准确精度，本文采用并行间隔来作为时间同步测量支撑，并采用优化的粒子群算法计算定位的最优值.文在粒子群优化算法的基础上，引入了随机性的Levy飞行机制来调节粒子的运动轨迹，这样不仅有助于跳出局部最优，且当粒子在全局最优附近时得到较好的收敛性.其主要作用在于当粒子在局部最优附近进行小范围的移动时，会突然给出一个较大步长的跳变使其跳出局部最优.在d维的空间下，粒子在t时刻改进后的速度V和位置X更新的公式为：

vd(t+1)=vd(t)+c1*(Pi(t)-xd(t))+c2*(Pg(t)-xd(t))

(44)

xd(t+1)=xd(t)+vd(t+1)+α*sign(rand-0.5)*levy(λ)

(45)

具有Levy飞行机制的粒子群算法的具体步骤如下：

1)对每个粒子进行初始化，设定种群大小，根据方程需要，随机生成各个粒子在设定维度下的初始解和速度值；

2)根据适应度方程，计算各个粒子的适应度值，并选出各个粒子的个体最优值，比较各个粒子的最优值确定粒子的全局最优值；

3)按照上面给出的式(44)，更新各个粒子的速度，并把速度限定在一定的范围内；

4)按照上面给出的式(45)，更新各个粒子的位置信息，并把位置限定在适应度函数所给的定义域内；

5)当得到的适应度值达不到要求或者迭代次数达不到规定的迭代次数时，返回到(2).

3 实验及分析

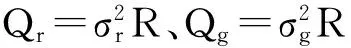
(46)

其中：u(l)为第u′次蒙特卡洛仿真得到的目标位置估计值，u′为目标真实位置，L=5 000为独立仿真运行次数.假设时差测量误差的均方根为σt，且满足σr=c·σt.图2中σg=-20 dB，σs=-40 dB.图3中σt=-60 dB，σs=-20 dB.图4中σt=-60 dB，σg=-20 dB.

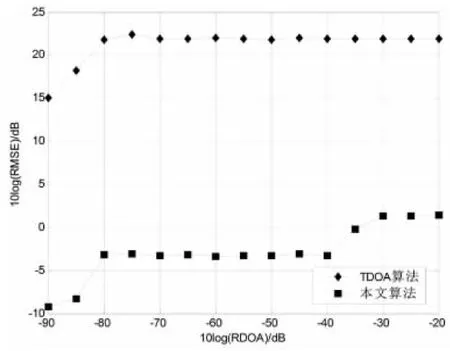
图2 误差随时差测量误差变化曲线图Fig.2 The ranging error results with RDOA

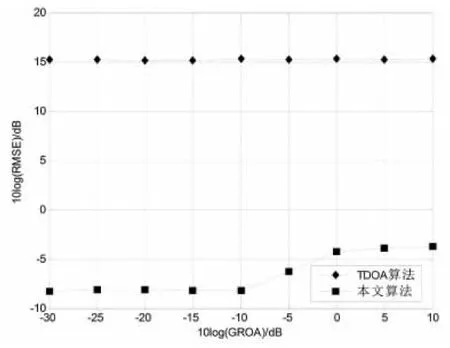
图3 误差随幅度比测量误差变化曲线图Fig.3 The ranging error results with GROA

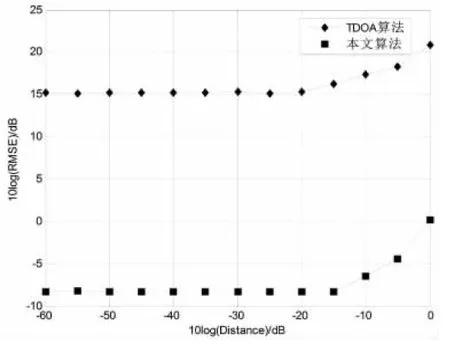
图4 误差随站址测量误差变化曲线Fig.4 The ranging error results with distance

从图2～4可以看出：

1)定位精度主要由TDOA和GROA测量误差中较小的参数决定，另一个参数误差变化对于定位结果的影响不明显；

2)引入并行分层时间间隔测量法后，在相同的参数测量误差条件下，本文提出的定位模型相比较TDOA模型大约可以提高25 dB，误差减少较为明显；

3)文算法在参数测量误差以及位置测量误差较小时，均方根误差都在-4 dB附近，且波动幅度变化不明显.

4 结论

本文提出了一种基于并行分层时间间隔测量的TDOA和GROA定位算法，引入含有约束条件下的两步加权最小二乘法来求解定位结果与目标方程之间的非线性关系.仿真和实验结果表明，特别是在参考节点有限制和抗干扰能力差的情况下，本文提出的定位算法相比TDOA算法有更为精确的定位性能.因此，本文算法相比其它改进的TDOA算法而言，不仅采用含有约束信息的最小二乘法来求解优化定位方程，而且同时克服传统时间同步的缺点，引入多层次间隔测量提高时间同步的精度，因此更适用于多节点和大规模的无线传感网络.

[1] HO K C.Bias Reduction for an Explicit Solution of Source Localization Using TDOA[C]//IEEE Trans Signal Process,2012,60(5):2101-2114.

[2] CARTER G C.Bi-iterative method for moving source localization using TDOA and FDOA measurements[C]//ELECTRONICS LETTERS,2015,51(1):8-10.

[3] 刘志先，赵荣阳.基于RSSI的室内定位改进算法[J].广西科学院学报,2015,31(1):69-72.

[4] HO K C,LU X,Kovavisaruch L.Source localization using TDOA and FDOA measurements in the presence of receiver location errors: analysis and solution[C]//IEEE Trans Signal Process,2007,55(2):684-696.

[5] 谭志，张卉.无线传感器网络RSSI定位算法的研究与改进[J].北京邮电大学学报,2013,36(3):88-91.

[6] HO K C，SUN Ming.Passive Source Localization Using Time Differences of Arrival and Gain Ratios of Arrival[J].IEEE Transactions on Signal Processing,2008,56(2):464-477.

[7] 郝本建，李赞，任妘梅，等.基于TDOAs与GROAs的多信号源被动定位[J].电子学报,2012,40(12):2374-2381.

[8] HAO B J,LI Z,WAN P W,et al.Bias Reduction for Passive Source Localization Based on TDOA and GROA[J].Acta Ectronica Sinica,2014,42(3):477-484.

[9] TE L K,PARHI K K.Optimized joint timing synchronization and channel estimation for OFDM systems[J].IEEE Transactions on Wireless Communications Letters,2012,1(3):149-152.

[10] ABDZADEH-ZIABARI H,SHAYESTEH M G.Robust timing and frequency synchronization for OFDM Systems[J]. IEEE Transactions on Signal Processing,2011,59(1):5538-5557.

[11] FOY W H.Position location solution by Taylor-series estimation[C]//IEEE Trans Aerosp Electron Syst.,1976,AES-12,(2):187-194.

[12] HO K C,XU W W.An accurate algebraic solution for moving source location using TDOA and FDOA measurements[C]//IEEE Trans Signal Process,2004,52,(9): 2453-2463.

[13] MING SUN,HO K C.An asymptotically efficient estimator for TDOA and FDOA positioning of multiple disjoint sources in the presence of sensor location uncertainties[J].IEEE Transactions Signal Process,2011,59(7):3434-3440.

[14] YU H G,HUANG G M,GAO J,LIU B.An efficient constrained weighted least squares algorithm for moving source location using TDOA and FDOA measurements[J].IEEE Transactions Wireless Communications,2012,11(1):44-48.

责任编辑：高 山

The TDOA Localization Algorithm Based on Parallel
Hierarchical Measurement

ZOU Dongyao1,LIU Biwei1,YANG Wei1，XIANG Jiayu2

(1.School of Computer and Communication Engineering,Zhengzhou University of Light Industry,Zhengzhou 450001,China;2.School of Mathematical Science,University of Science and Technology of China,Hefei 230026,China)

The precise time synchronization technology is required by the time difference of arrival (TDOA) positioning algorithm.Under the low precision of traditional time synchronization technology,this paper proposes a joint positioning algorithm gain ratio of arrival based on the TDOA and GROA of a parallel hierarchical time interval measurement.Firstly,we establish the optimization equation containing Lagrange coefficient based on TDOA and GROA joint positioning model.And then we solve the equation by constrained weighted least squares algorithm (TSWLS); at the same time,we use the method of parallel hierarchical time interval measurement to control the time synchronization of positioning model.The experiment and analysis show that the proposed algorithm accuracy increases by 25 dB compared with the traditional TDOA location algorithm,which has relatively stable and high positioning precision.

time synchronization;time differences of arrival (TDOA);gain ratios of arrival (GROA);least squares;parallel hierarchical measurement

2016-10-11.

河南省高等学校重点科研项目(15A520109)；河南省科技厅科技攻关项目 (112102210321)；河南省产学研合作项目 (122107000022)；研究生科技创新基金项目.

邹东尧(1973- )，男，博士，副教授，主要从事物联网、无线传感网络定位以及信息处理的研究.

1008-8423(2016)04-0435-07

10.13501/j.cnki.42-1569/n.2016.12.017

TP393

A