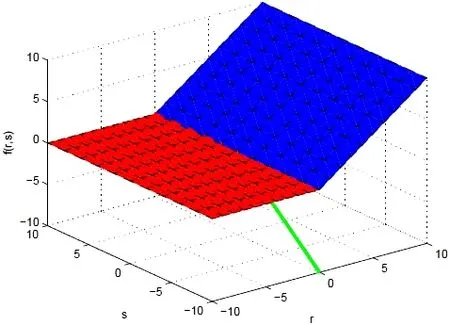
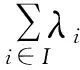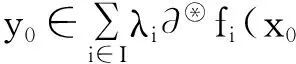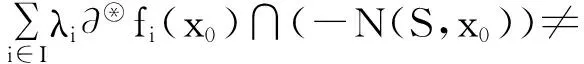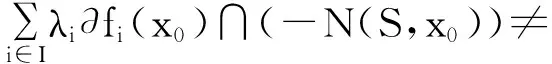拟凸多目标规划问题解的最优性条件
2017-01-13陈荣波李美术
陈荣波,高 英,李美术
(重庆师范大学 数学科学学院,重庆 401331)
拟凸多目标规划问题解的最优性条件
陈荣波,高 英*,李美术
(重庆师范大学 数学科学学院,重庆 401331)
考虑约束集为凸集,目标函数为拟凸函数的多目标规划问题,利用次微分为工具研究拟凸多目标规划问题的最优性条件.在拟凸单目标规划问题最优性条件的基础上,在一定约束条件下,利用标量化方法得到拟凸多目标规划问题的最优性条件.
多目标规划;拟凸函数;次微分;最优性条件
在拟凸规划问题中,最优性条件是一个被广泛应用的概念,最优性条件对于研究向量优化问题的解有着重要理论指导意义.拟凸规划是现代数学规划中的一个重要研究领域.在工程技术、环境污染以及机器人运行轨道设计等工业问题中都有着广泛应用.文献[1]首次提出关于一类凸极值规划问题的解集特征和最优性条件的概念,随后一些学者将凸规划问题中的结论推广到一些其它类型的规划问题.如文献[2-3]研究了无限维凸规划问题的最优性条件,文献[4-6]研究了广义凸规划问题的最优性条件,文献[7]研究了凸向量规划问题的最优性条件,文献[1,8]研究了拟凸单目标规划问题的最优性条件.文献[9]利用SlaterCQ研究了拟凸半无限规划问题的最优性条件.近年来,国内外越来越多的学者开始致力于拟凸规划问题的理论研究,但是关于拟凸多目标规划问题最优性条件的研究并不多.
本文研究了如下形式的拟凸多目标规划问题:
这里fi是Rn上的拟凸函数,i∈I={1,2,…,p},拟凸函数是指∀x1,x2∈S,λ∈(0,1)总有f[λx1+(1-λ)x2]≤max{f(x1),f(x2)}成立.可行集S是Rn的凸子集.
本文在文献[4,10]的基础上,在一定约束品性下研究了一类拟凸多目标规划问题的最优性条件和解集特征.具体结构如下:在第2节,给出了一些基本概念和结论,并介绍了几种次微分.在第3节,利用文献[4]和文献[10]在一定约束条件下,利用标量化的思想给出了拟凸多目标规划问题的有效解、弱有效解、真有效解和最优性条件.
1 预备知识

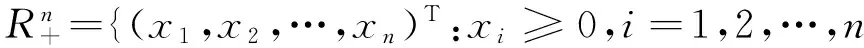
设x=(x1,x2,…,xn)T,y=(y1,y2,…,yn)T∈Rn,定义向量x,y的序关系:
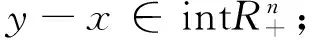
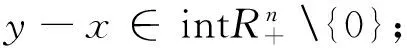
xy⇔
定义1[10]点z∈S称作问题(MOP)的弱有效解当且仅当找不到x∈S使得:
fi(x) 定义2[10]点z∈S称作问题(MOP)的有效解当且仅当找不到x∈S使得: fi(x)≤fi(z),∀i∈I, fs(x) 定义3[4]g:Rn→R∪{±},假设g在x0∈S处是有限的.g在x0处水平集和严格水平集的定义如下: [g≤g(x0)]={x∈X:g(x)≤g(x0)},[g 定义4[11]经典Greenberg-Pierskalla次微分定义如下: 定义6[12]凸集C⊂Rn在x0处的法锥定义如下: 很显然, ∂g(x0)=N([g 当g在[g 且x0是g的最优解当且仅当0∈∂*g(x0)或∂*g(x0)=Rn或∂g(x0)=Rn. 另外一类在广义凸性理论下闭的且完全不同的经典次微分形式如下. 定义7[13]Gutierrez次微分定义如下: 定义8[14]Plastria下次微分定义如下: x0是g的最优解当且仅当0∈∂≤g(x0),0∈∂ 显然,有: ∂≤g(x0)⊂∂ 文献[4]针对(MOP)问题中p=1时的情况,利用Greenberg-Pierskalla次微分给出拟凸单目标规划问题的最优性充分条件. 引理1[4]设存在x0∈S都有∂*f1(x0)∩(-N(S,x0))≠∅,则x0是f1在S上的最优解. 文献[10]中研究了一类带有线性不等式约束的非光滑向量伪凸多目标规划问题(NMOP). 其中aj∈Rn,bj∈R.且fi:K→R,i∈I={1,2,…,p}是开凸集K上的局部Lipschitz伪凸线性函数. 引理3[12]设S是Rn上非空开凸集,f:S→R在S上可微的伪凸函数,则f也是严格拟凸和拟凸函数. 在拟凸单目标规划问题的最优性条件的基础上,将结论推广到拟凸多目标规划问题的最优性充分条件. 定理1对于(MOP)问题,若存在x0∈S,使得: (1) 则x0是f在S上的弱有效解,其中λi≥0,且至少有一个λi>0,i∈I. 证明反证.假设x0不是(MOP)的弱有效解,则存在x∈S使得:f(x) 即〈y0,x-x0〉<0,又由于y0∈-N(S,x0),则∀x∈S,有〈y0,x-x0〉≥0,矛盾.从而f(x0)为原问题的弱有效解. 定理2对于(MOP)问题,若存在x0∈S,使得: (2) 则x0是f在S上的有效解,其中λi≥0,i∈I且至少存在一个i∈Ix0⊂I,使λi>0,Ix0={i|fi(x) 〈y0,x-x0〉<0, 又: y0∈-N(S,x0). 这表明∀x∈S: 〈-y0,x-x0〉≤0. 矛盾,故x0是f在S上的有效解. 定理3对于(MOP)问题,若存在x0∈S使得: (3) 则x0是f在S上的真有效解,其中λi>0,i∈I. 证明由引理2和引理3显然成立. 推论1假设存在x0∈S使得f在[f ∂f(x0)∩(-N(S,x0))≠{0}. (4) 证明在假设条件下,由∂f(x0)=∂*f(x0)∪{0},则式(4)能推出式(2). 推论2假设f在[f (5) 则x0是f在S上的有效解. 证明在可微条件下,f的次梯度和梯度向量是等价的,由定理1可知: 则上式成立. 下面举例说明在上面两个推论的证明中上半连续这个条件是非常关键的. 图1 f2的函数图像Fig.1 Function plot for f2 例1令X=R2,S=R-×R,f=(f1,f2),其中f1(r,s)=r, 但是x0不是f在S上的有效解. 一些限制条件的提出是为了满足式(1)必要性的成立,注意到即使在凸性条件下,为了得到必要性条件也必须要满足一些限制条件.下面给出了证明. 定理4设x0是(MOP)问题的有效解,但是x0不是f在X的局部有效解,则: 证明集合G=[f 〈y0,w-x0〉≥r≥〈y0,u-x0〉,∀w∈F,∀u∈G. 取w=x0,得到r≤0,有: y0∈∂fi(x0), 存在λi>0,i∈I使得: 当G是开集时,有: y0∈∂*fi(x0), 存在λi>0,i∈I使得: 假设x0不是f在X上的局部有效解,存在任意靠近x0的点u∈G使得r=0,即: -y0∈N(F,x0). 下面的例子为了说明x0不是局部有效解这个条件不可省略. 例2设f=(f1,f2):R→R定义如下,其中f1(x)=x, 令S=[0,1],对于x0=0,它不是f的局部有效解. ∂*f1(x0)=∂*f2(x0)=(0,+),-N(S,x0)=R+, 然而对于x0=1,∂*f1(x0)=∂*f2(x0)=(0,+),-N(S,x0)=R+,对任意λi>0都不会成立.但x0=1是f的局部有效解. 推论3设f是拟凸函数,S是X的凸子集,x0∈S不是f在X的局部有效解.假设f在[f≤f(x0)]上每一点都是上半连续,则x0是f在S上的有效解当且仅当: 其中λi>0,i∈I. 证明由∂fi(x0)∩(-N(S,x0))≠∅,i=1,2,…,p, 推论4设f在X上是连续拟凸函数,X上的局部有效解就是全局有效解,令inff(S)>inff(X).假设f在[f≤inff(S)]上是Lipschitzian,则下面的结论在x0∈S上是等价: i)x0是f在S上的有效解; ii)∂≤f(x0)∩(-N(S,x0))≠∅; iii)∂ 证明证明方法同推论3一样. [1] MANGASARIAN O L.A simple characterization of solution sets of convex programs[J].OperationsResearch Letters,1988,7(1):21-26. [2] JEYAKUMAR V,WOLKOWICZ H.Generalizations of Slater′s constraint qualification for infinite convexprograms[J].Mathematical Programming,1992,57(1/2/3):85-101. [3] JEYAKUMAR V.Infinite-dimensional convex programming with applications to constrained approximation[J].Journal of Optimization Theory & Applications,1992,75(3):569-586. [4] PENOT J P.Characterization of Solution Sets of QuasiconvexPrograms[J].Journal of OptimizationTheory & Applications,2003,117(3):627-636. [5] JEYAKUMAR V,YANG X Q.Convex composite multi-objective nonsmoothprogramming[J].MathematicalProgramming,1993,59(1/3):325-343. [6] JEYAKUMAR V,LEE G,DINH N.Lagrange Multiplier Conditions Characterizing the Optimal SolutionSets of Cone-Constrained Convex Programs[J].Journal of Optimization Theory & Applications,2004,123(1):83-103. [7] JEYAKUMAR V,LEE G M,DINH N.Characterizations of solution sets of convex vector minimizationproblems[J].European Journal of Operational Research,2006,174(3):1380-1395. [8] QUYENT.Optimality conditions in quaiconvex vector optimization[J].Southeast-Asian J,2014,3(1):24-32. [9] KANZI N,SOLEIMANI-DAMANEH M.SLATER CQ.Optimality and duality for quasiconvex semi-infiniteoptimization problems[J].Journal of Mathematical Analysis & Applications,2016,434(1):638-651. [10] MISHRA S,UPADHYAY B,AN L.Lagrange Multiplier Characterizations of Solution Sets of ConstrainedNonsmoothPseudolinear Optimization Problems[J].Journal of Optimization Theory & Applications,2014,160(3):763-777. [11] PENOT J P.Are Generalized Derivatives Sseful for Generalized Convex Functions?[M].Springer US:Generalizedconvexity,generalized monotonicity:recent results,1998:3-59. [12] CLARK F H.Optimization and NonsmoothAnalysis[M].New York:Wiley-Interscience,1983. [13] GUTIERREZ J M.Infragradientes y direcciones de decrecimiento[J].Revista de la Real Academia de Ciencias Exactas Fisicas y Naturales,Madrid,1984,78(4):523-532. [14] PLASTRIA F.Lower subdifferentiable functions and their minimization by cutting planes[J].Journalof Optimization Theory and Applications,1985,46(1):37-53. 责任编辑:高 山 Optimality Conditions in Quasiconvex Multiobjective Programs CHEN Rongbo,GAO Ying*,LI Meishu (College of Mathematics Science,Chongqing Normal University,Chongqing 401331,China) In this paper,we consider a quasiconvex multiobjective programming problem where the objective is quasiconvex and constraint set is convex.By using subdifferential as a tool.we study the optimality conditions in quasiconvex multiobjective programming. Based on the optimality conditions in quasiconvex multiobjective programming problem and under certain constraint conditions,optimality conditions of quasiconvex multiobjective programming problem are derived. Multiobjective programming;Quasiconvex function;subdifferentials;optimality conditions 2016-10-21. 重庆市教委科学技术研究项目(KJ1500309,KJ1400519);重庆市基础与前沿研究计划项目(cstc2015jcyjA00005). 陈荣波(1992- ),男,硕士生,主要从事多目标规划的研究;* 高英(1982- ),女(蒙古族),博士,副教授,主要从事最优化理论与方法的研究. 1008-8423(2016)04-0386-05 10.13501/j.cnki.42-1569/n.2016.12.006 O221.6 A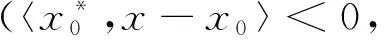
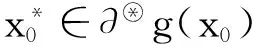



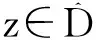




2 最优性必要条件