物体拍摄位置定位模型的研究
2017-01-13冯雅云库在强
冯雅云,库在强,周 燕
(1.黄冈师范学院 数理学院,湖北 黄州 438000;2.武汉市天门墩中学,湖北 武汉 430015)
物体拍摄位置定位模型的研究
冯雅云1,库在强1,周 燕2
(1.黄冈师范学院 数理学院,湖北 黄州 438000;2.武汉市天门墩中学,湖北 武汉 430015)
太阳影子定位技术可以通过分析视频中物体的影子变化来确定视频的拍摄位置。首先,根据影长与物体高度、拍摄时间、标准时间、经纬度和大气折射率等参数之间的关系,建立了物体影长模型。其次,若已知物体不同时刻的影子测量坐标时,由于影长和影子角度偏转量的理论值现仅与物体高度和经纬度有关,可根据影长与影子角度在某位置的理论值和实际值之间的总误差最小,建立确定物体拍摄位置的模型。最后,先采用全局搜索法,在限定影长和角度偏转量总误差范围的条件下,给出了决策变量的粗略范围。在此基础上再采用局部搜索法,进一步缩小影长和角度偏转量总误差的限定范围,最后搜索出较为合理的拍摄位置。
影子定位;影长;角度偏转量
确定视频的拍摄时间和位置是视频数据分析中的重要方面,而太阳影子定位技术就可以通过分析视频中物体的影子变化建立合理的模型,确定出视频的拍摄位置。2010年,郑鹏飞等[1]建立了时间、太阳位置和影子轨迹关系的数学模型,为求得影长与物体高度,所处经纬度,视频拍摄时间,时间和大气折射率等参数之间的关系式奠定了基础。同期,杜春旭等[2]比较了几种常见的计算太阳位置的简单方法,最后发现Bourges的赤纬角算法和Lamn的时差算法的精度远优于其他算法,并总结出了一种算法简单的高精度太阳位置计算方法。张文华等[3]以国家地面气象规范的相关理论和公式为基础,采用Edlen公式对大气折射进行了修正,提出了太阳高度角和方位角的修正公式。以上文献的研究内容和方法为影长模型的建立、物体拍摄位置模型算法的优化以及视频数据的处理提供了理论依据。但是,对太阳位置和影子轨迹关系还存在着一些不适之处,需要在此基础上考虑大气折射对影子的影响,同一经度上的标准时间与地方时间之间的时差以及赤纬角、时角计算的精确算法,因此需要改进物体影长模型。同时,在搜索物体拍摄位置的过程中,如果限定影长和角度偏转量的误差范围,并通过拟合所得的物体影子曲线以及标准时间、地方时和经度之间的转化得到物体经度的大致范围。这都有利于优化模型的算法,提高模型算法的求解速度。
1 物体影长模型
1.1 模型假设
(1)形成物体影长的太阳光近似看做平行光;
(2)大气层是均匀等密度的,折射率约为1.000 277;
(3)物体所在的地面是水平的;
(4)将地球和太阳在运行中不规则变化和周期性变化产生的误差忽略不计;
(5)假设地球自转一圈的时间为24小时整,且视频拍摄时间都在2015年。
1.2 实物影长模型
设h0为太阳高度角,α为方位角,φ为纬度,φ为经度,δ为赤纬角,ω为太阳时角。L为影长,H为物体高度;将影长分别沿X轴和Y轴投影分别为x0,y0;影长坐标为(x0,y0)。N为按天数顺序排列的积日,例如当时间为1月1号时,N=1,时间为3月22日时,N=81;Y为年份,int(x)则表示为取不大于X的最大整数。
结合文献[4-5]提供的方法,可以得到实物影长模型:
(1)
其中,
2 物体影长变化曲线
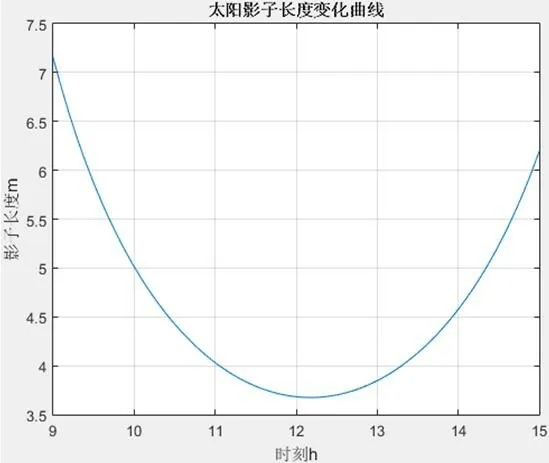
图1 太阳影子长度变化曲线
以拍摄时间在10月22日,位置位于天安门的3m高的直杆为例[6],其中天安门广场的地理位置为(E 116.391°,N 39.907°),且N=295。通过Matlab软件编程可以得到3m高的直杆在北京时间9∶00~15∶00之间的影长变化曲线如图1所示。同时根据Matlab软件计算的结果,可以得到9∶00~15∶00中各整点时的影长,如表1所示。分析图1和表1可发现从9∶00~12∶20左右的过程中影子长度逐渐减小,而12∶20~15∶00的过程中影子长度又逐渐增大;大概在12∶20左右,由Matlab计算发现此时影子长度达到最小,大概为3.6748 m。整段时间内的影长在3.6~7.2 m之间。

表1 9∶00~15∶00中各整点的影长表
3 物体拍摄位置模型
当已知物体某天不同时刻的影子测量坐标时,由影长模型可发现影长和影子角度偏转量的理论值仅与物体高度和经纬度有关,此时可以利用长度和角度信息确定出物体的位置。
3.1 影长偏差模型
若由物体在不同时刻的影子测量坐标(xi,yi)(i=1,2,3,…,n),需要确定物体的拍摄位置。设地球上任意位置(φ,φ)在第i个时刻的影长的理论值为L(i),实际值为L0(i),H为物体高度,(在实际情况下,可将其限制在100m),φ为纬度,η为大气折射率,约为1.000 277。

(2)
以拍摄位置下各时刻影长的理论值与实际值之间的总误差最小为目标函数,可建立的单目标规划的影长偏差模型为:
(3)
其中决策变量为经纬度φ、φ和物体高度H。
同时:
(4)
(5)
3.2 角度偏转偏差模型
如果将经度的范围限制在φ0-10°到φ0+10°之间,可求解出任意时间段内的物体影子角度偏转量,即影子在这段时间内所转过的角度。设第i个时刻物体的影子与x轴的理论夹角为θ(i),实际夹角为θ0(i)。若在整个时间段内,影子实际所转过的角度比较小,就可以用总的影子角度偏转量θ0来替代描述各个时间段内的影子角度偏转量;若总的角度偏转量比较大,就需要对影子角度偏转量的描述情况加以修正,以从初始时刻到各个时刻(第1个时刻到第i个时刻)之间的影子角度偏转量来替代描述各时间段内的影子角度偏转量。本文主要考虑以下两种情况的角度偏转量。
情况1:若总的角度偏转量较小,以拍摄位置下总的影子角度偏转量的理论值与实际值之间的误差最小为目标函数,建立的角度偏转偏差模型为:
(6)
其中决策变量为经纬度φ、φ和物体高度H。
情况2:若总的角度偏转量较大,以各个时刻与初始时刻之间的影子角度偏转的理论值Δθ(i)与实际值Δθ0(i)之间的总误差最小为目标函数,建立的角度偏转偏差模型为:
(7)
其中决策变量为经纬度φ、φ和物体高度H;
且

(8)

(9)
其中θ(i)表示在第i个时刻物体影子与x轴夹角的理论值,θ0(i)则表示在第i个时刻物体影子与x轴夹角的实际值。
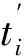
(10)
(11)
(12)
3.3 物体拍摄位置改进模型
如果考虑长度和角度双重因素,将影长偏差模型和角度偏转偏差模型结合起来,就可建立改进的多目标规划的物体拍摄位置模型。
(1)若总的影子角度偏转量比较小,则物体拍摄位置模型为:
(13)
(2)若总的影子角度偏转量比较大,则物体拍摄位置模型为:
(14)
其中经纬度φ、φ和物体高度H为决策变量。
4 模型算法
虽然影长偏差模型和角度偏转偏差模型以及物体拍摄位置模型,都是在已知物体影子顶点坐标、拍摄时间及标准时间的条件下,确定物体可能的拍摄位置,但在模型算法存在异同。
4.1 模型算法的相同点
全局搜索法。第一次采用全局搜索法,经度的范围在φ0-10°到φ0+10°之间;纬度在-90°到90°之间;且经纬度的步长分别都为0.1°(因为第一次搜索的目的是为了得到经纬度的一个大致的范围,所以步长不需要很小);物体高度的范围在0~100 m,为得到一个大致范围,物体高度的步长定为0.1m。
局部搜索法。第二次采用局部搜索法,经纬度和物体高度的范围为第一次全局搜索所得到的粗略结果。同时经纬度的步长缩小为0.01°(因为第二次搜索的目的是为了得到物体所处的精确位置,所以需要通过缩短步长来提高结果的准确度),且物体高度的搜索步长定为0.01m。
4.2 模型算法的不同点
在搜索的过程中需要加入影长和角度偏转误差的限定范围有所不同。
采用全局搜索法时,物体拍摄位置模型加入的限定范围为:
(15)
或
(16)
采用局部搜索法时,物体拍摄位置模型的限定范围进一步缩小为:
(17)
或
(18)
5 算法实例及误差分析
已知拍摄时间为2015年4月18日,拍摄物体为直杆,具体数据是在14∶42~15∶42之间的每隔三分钟所测量的21组影子顶点坐标[6],利用物体拍摄位置模型确定出直杆的拍摄位置。
由Matlab拟合可得此时物体的影子曲线为:L=0.148 9t′2-3.751 9t′+24.127 5,拟合的残差平方和为1.648 9×10-5,误差极小,拟合效果好。曲线具有最低点为t′≈12.598 7h,φ0≈111.02°,物体的经度在111.02°附近。14∶42时影子与x轴的实际夹角θ0(1)≈25.631 1°,15∶42时影子与x轴的实际夹角θ0(21)≈18.555 2°,则影子实际所转过的总角度θ0=|θ0(21)-θ0(1)|,约为7.075 9°。那么这段时间内影子角度的均匀转速约为0.117 9°/min,所以在3分钟内影子角度的偏转量比较小,因此可以用总的角度偏转量来替代描述各个时间段内的角度偏转量。可利用前一种物体拍摄位置模型及其模型算法确定出直杆的位置,同时在搜索过程中要将杆长的范围限制在0~10 m之间,这样才具有一定的普遍性。
采用全局搜索法,得到决策变量的大致范围为:φ∈(106.32°,115.63°),φ∈(16.2°,25.6°)以及H∈(1.5 m,2 m);在此基础上,再采用局部搜索法,得到直杆拍摄位置的若干组可能取值发现,当直杆的杆长为1.99 m,满足限定范围的拍摄位置可能有:(E109.50°,N18.30°),(E109.50°,N18.31°),(E109.51°,N18.31°);最后取其平均值,那么直杆大概在(E109.503°,N18.307°)附近,位于海南省三亚市。
运用物体拍摄位置模型及其算法所得到的拍摄位置,在各个时刻的影长的误差以及各个时间段内的影子角度偏转的误差,分别不超过0.002 5 m和0.002 1°,影长的相对误差不超过0.21%.且影长的总误差为0.034 6 m,影子角度偏转量的总误差为6.750°×10-5,误差都控制在极小的范围之内。由此可以说明物体拍摄位置模型和模型的算法较为合理,具有可行性。
[1] 郑鹏飞,林大均,刘小羊,等. 基于影子轨迹线反求采光效果的技术研究[J]. 华东理工大学学报(自然科学版), 2010, 36(3):458-463.
[2] 杜春旭,王普,马重芳,等. 一种高精度太阳位置算法[J]. 能源工程, 2010(2):41-44.
[3] 张文华,司德亮,徐淑通,等. 太阳影子倍率的计算方法及其对光伏阵列布局的影响[J]. 太阳能, 2011(9):28-31.
[4] 孙吉山,洪薇. 北京标准时间和各地真太阳时的换算法[J]. 上海针灸经络研究所, 1994, 13(1):25-26.
[5] 张宏义,刘敬民. 俯仰角大气折射误差修正方法[J]. 光电技术应用. 2008, 23(4):25-27.
[6] 中国数学建模网[EB/OL]. http://www.shumo.com/home/html/3158.html,2016-03-12.
责任编辑 喻晓敏
The research of the model on the filming location
FENG Ya-yun1, KU Zai-qiang1, ZHOU Yan2
(1.College of Mathematics and Physics, Huanggang Normal University, Huangzhou 438000, Hubei, China;2.Wuhan Tianmendun Middle School, Wuhan 430015, Hubei,China)
The sun's shadow positioning technology is based on the analysis of the change on shadow of the objects in the video to determine the video filming position. First of all, according to the relationship between the parameters such as the heights of a shadow and an object, time, standard time, latitude and longitude and the atmospheric refractive index, we could establish the model of the object shadow. Then, if the shadow coordinate on the object of different time is known, because the theoretical value of the length of shadow and the shadow angle deflection is only related with the object height and latitude and longitude, according to the shadow length and the shadow angle in a certain position of total minimum error between theoretical value and realitic value, we could determine the object model of the filming location. Finally, using the global search method, limiting the total error ranges about the shadow length and angle of deflection, rough scope of decision variables is given. Again on this foundation, we used the local search method to further reduce the total error of shadow length and angle of deflection, and finally could search out the reasonable position.
shadow positioning; shadow length; angle deflection amount
O29
A
1003-8078(2016)06-0055-05
2016-09-14 doi 10.3969/j.issn.1003-8078.2016.06.15
冯雅云,女,湖北黄州人,黄冈师范学院数理学院2015级硕士研究生。
库在强,男,湖北武穴人,副教授,主要研究方向为数学教育和系统最优化。
