多元向量值函数求导的矩阵表示及其在人工神经网络中的应用

杨迪威，边家文，张玉洁

(中国地质大学 数理学院，湖北 武汉 430074)

多元向量值函数求导的矩阵表示及其在人工神经网络中的应用

杨迪威，边家文，张玉洁

(中国地质大学 数理学院，湖北 武汉 430074)

在介绍多元向量值函数求导的矩阵表示的基础上，给出了梯度下降法的工作原理及其训练神经网络的过程，最后通过Matlab仿真实验验证了梯度下降法的有效性.

人工神经网络； 深度学习； 梯度下降法； 多元函数导数的矩阵表示

2016年3月，谷歌Deep Mind团队开发出的一款围棋人工智能程序——阿尔法围棋(AlphaGo)战胜了世界围棋冠军李世石，这让世人惊叹于人工智能迅猛发展的同时，也让人们认识到一种新的机器学习技术——深度学习(Deep Learning)[1]．深度学习是一种深层的人工神经网络(Artificial Neural Network)[2-3]，试图通过模拟大脑认知的机理去解决机器学习中的问题[4-5]．目前，深度学习有三大基础网络模型：自编码器(Auto Encoder, AE)网络、受限玻尔兹曼机(Restricted Boltzmann Machine, RBM)以及卷积神经网络(Convolution Neural Network, CNN)，而这3种模型均采用梯度下降法(Gradient Descent)对网络进行训练[6-7]．因此，深入理解梯度下降法对掌握此项新的机器学习技术是非常必要的．为此，笔者将从高等数学中多元函数导数、梯度等基本概念出发[8]，深入浅出地介绍梯度下降法的工作原理及其训练神经网络的算法过程，最后通过在Matlab[9]环境下函数拟合仿真实验验证梯度下降法的有效性.

1 多元向量值函数的导数

多元向量值函数是一种具有多个自变量和多个因变量的结构复杂函数，为了便于研究多元向量值函数求导规律，先给出多元向量值函数导数的矩阵表示．

1.1 多元向量值函数导数的矩阵表示

定义1多元函数的导数．设x=(x1,…,xm)T，则多元函数y=f(x)的导数定义为

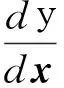
(1)

定义2多元向量值函数的导数．设x=(x1,…,xm)T，y=(y1,…,yn)T，多元向量值函数y=f(x)为

(2)

其中，fi(x)(i=1,2,…,n)为m元函数，则多元向量值函数y=f(x)的导数定义为

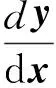
(3)

根据定义2，容易得出结论：

结论2 设o=(o1,…,om)T，z=(z1,…,zm)T，若多元向量值函数o=f(z)定义为

(4)

dodz=f'(z1)0…00f'(z2)…0︙︙…︙00…f'(zm)æèççççöø÷÷÷÷

≜diag(f′(z1),f′(z2),…,f′(zm)) ，

(5)

(6)

1.2 多元向量值函数的求导法则根据多元向量值函数的导数的矩阵表示，可以得到其运算规律．

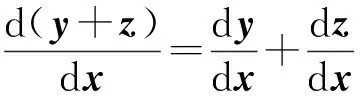
(7)

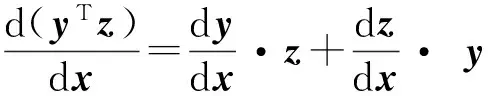
(8)

本文只给出乘法法则的证明．

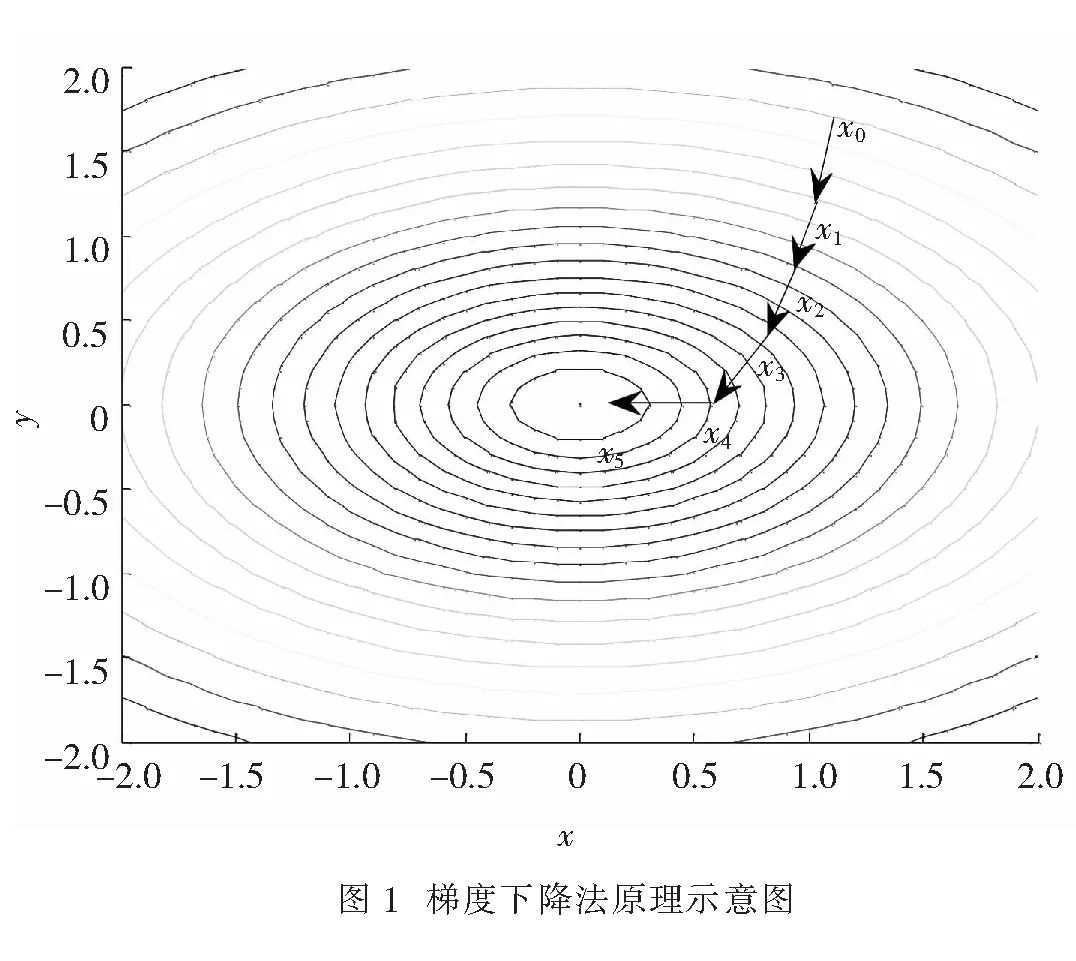
1.3 梯度下降法已知多元函数对各个自变量的偏导数组成的向量也称为梯度，表示该函数的方向导数取到最大值的方向[8]．在几何上，函数的梯度又代表着该函数等值线的法线方向．基于这些特点，函数梯度可以被用于求函数极值问题．图1给出了二元函数z=x2+2y2的等值线，为了找到该函数的极小值点，可以先在定义域平面内随机地找一点x0，求出该点的梯度，并沿着梯度所指相反方向以设定的步长(学习率)lr移动到点x1，接着用类似的方法循环迭代依次找到点x2，x3，…，最终可以不断逼近该函数的极小值点．上述过程就是优化算法中常用的梯度下降法的工作原理[7]．

2 梯度下降法在人工神经网络中的应用

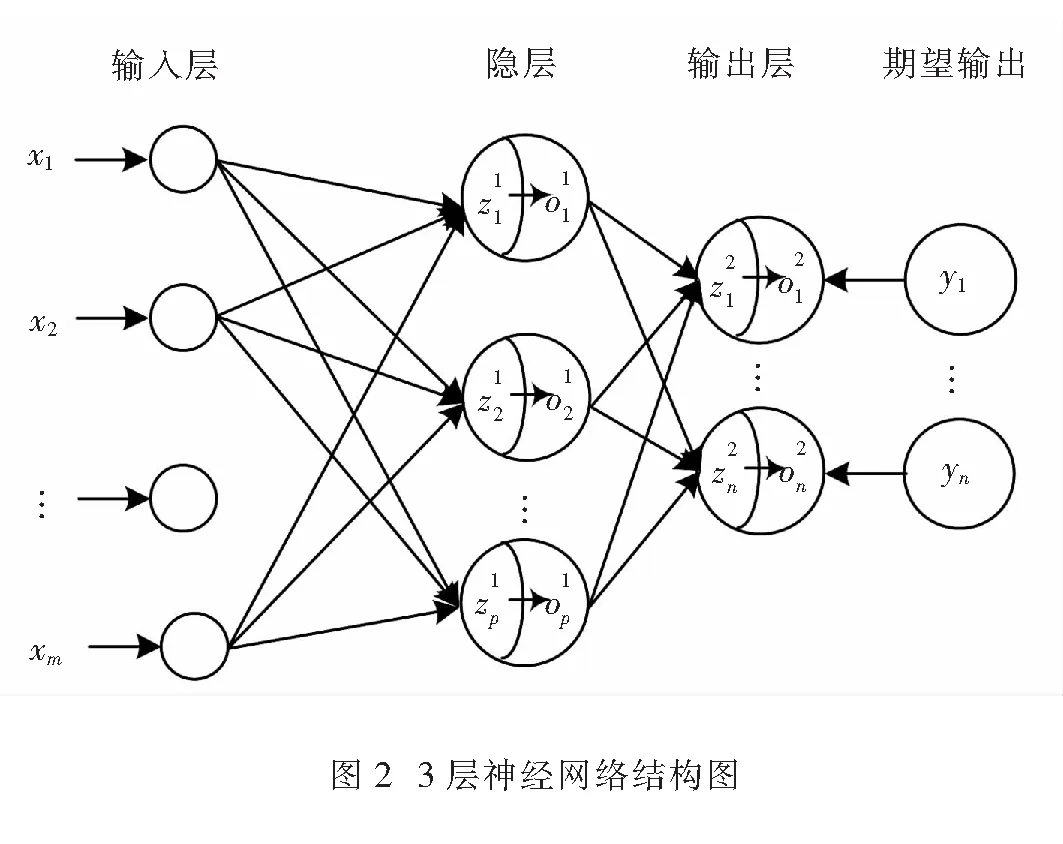
梯度下降法是神经网络中基础训练算法，比如，深度学习中的三大基本模型：自编码器、受限玻尔兹曼机以及卷积神经网络均采用梯度下降法对网络进行训练．以三层BP神经网络为例(如图2所示)，介绍梯度下降法训练神经网络的算法过程．

算法主要包含2个过程，第一个过程，利用样本输入向前逐层计算，得到网络输出；第二个过程，以期望(样本)输出与网络实际输出之间误差为目标函数，利用梯度下降法反向逐层调整网络参数．2个过程迭代进行，以期目标函数达到最小．

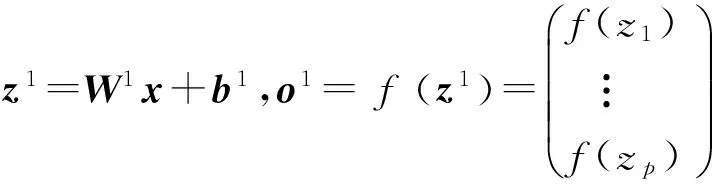
(10)

z2=W2o1+b2，o2=z2.

(11)

2.2 误差的反向传播给定网络期望(样本)输出y=(y1,…,yn)T，可得到网络误差为

(12)

按照梯度下降法对各层的权值和偏置进行修正，使得网络误差最小化．

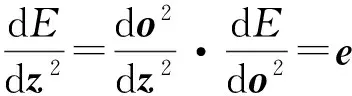
(13)

通常δ2称为输出层的灵敏度．于是可进一步根据式(11)，求得隐层与输出层之间权值和偏置的导数表达式为

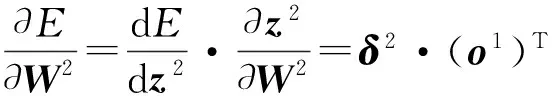
(14)

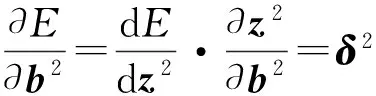
(15)

从而按照梯度下降法，得到对隐层与输出层之间权值和偏置的修正

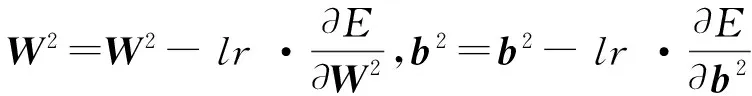
(16)

其中，lr称为学习率，为一个预先设定的常数．

2) 隐层计算 类似于输出层的计算过程，首先求隐层的灵敏度

(o1≜(1-o1))≜((W2)T·δ2)≜δ1，

(17)

其中，≜表示向量对应元素相乘．其次，可根据式(10)得到输入层与隐层间的权值和偏置的导数表达式

(18)

(19)

最终，得到对W1和b1的修正

(20)

3 应用举例

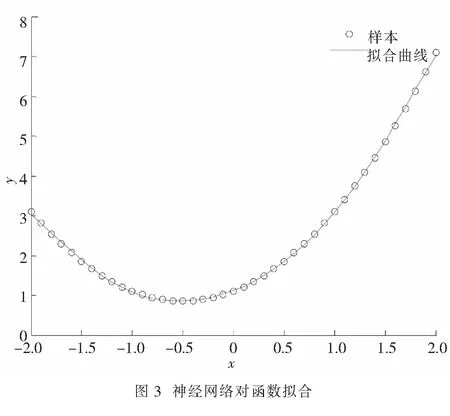
给定函数f(x)=x2+x+1,在区间[-2,2]上等间距抽取数据点xk，k=1,2,…,K，相应地取yk=f(xk)+εk，其中εk为服从均值为零、均方差为0.5的独立同分布高斯噪声,建立图2所示的3层神经网络，并对该函数进行拟合．

在Matlab环境下，求解过程如下：

首先，构造神经网络中的sigmoid函数：

functiony=sigmoid(x)

y=1./(1+exp(-x));

end

然后，使用梯度下降法对神经网络进行训练:

x=-2:0.1:2;y=x.^2+x+1;y=y+normrnd(0,0.5); %产生含噪样本

%%%max_epoch为训练次数；err_goal为期望误差最小值；lr为学习率%%%

max_epoch=10000;err_goal=0.001;lr=0.1;

%%%m为输入层维数；p为隐节点数；k为样本个数；n为输出层维数%%%

[m,k]=size(x);p=12;[n,k]=size(y);

%网络参数初始化

w1=rands(p,m);b1=rands(p,1);w2=rands(n,p);b2=rands(n,1);

forepoch=1:max_epoch

o1=sigmoid(w1*x+repmat(b1,[1,k])); %计算隐含层的输出

o2=w2*o1+repmat(b2,[1,k]); %计算输出层输出

E=( (o2-y)’*(o2-y) )/2; %网络输出与期望输出误差

if(E

%%%%调整输出层权值和偏置%%%%

e=o2-y;

delta2=e; %输出层灵敏度

dw2=delta2*o1’/k;db2=mean(delta2,2); %输出层权值和偏置的梯度

w2=w2-lr*dw2;b2=b2-lr*db2; %输出层权值和偏置的修正

%%%%调整隐含层权值和偏置%%%%

delta1=(o1.*(1-o1) ).* (w2’*delta2 ); %隐含层灵敏度

dw1=delta1*x’/k;db1=mean(delta1,2); %隐含层权值和偏置的梯度

w1=w1-lr*dw1;b1=b1-lr*db1; %隐含层权值和偏置的修正

end

%%%%训练好的神经网络对函数拟合%%%

o1=sigmoid(w1*x+repmat(b1,[1,k]));

o2=w2*o1+repmat(b2,[1,k]);

plot(x,y,’o’,x,o2,’-’); %绘制拟合结果

xlabel(’x’);ylabel(’y’);legend(’样本’,’拟合曲线’)

图3为函数f(x)=x2+x+1的拟合效果图．从图3中容易看到，用神经网络对函数拟合能取得较好的效果．因此，梯度下降法是一种十分有效的神经网络训练算法．

4 小 结

介绍了多元向量值函数导数的矩阵表示法及其运算性质，并将其应用于神经网络参数训练，最后Matlab仿真实验展示了多元向量值函数求导在神经网络中应用的有效性，扩展了《高等数学》多元函数导数的学习内容，同时将高等数学中多元微分学基本概念和方法应用于人工智能前沿领域，有益于培养学生对数学知识的兴趣，激发学生的学习热情．

[1] 田渊栋. 阿法狗围棋系统的简要分析[J]. 自动化学报. 2016, 42(5): 671-675.

[2] 王小川.Matlab神经网络43个案例分析[M]. 北京：北京航空航天大学出版社, 2013.

[3] 焦李成，杨淑媛，刘芳，等. 神经网络七十年:回顾与展望[J]. 计算机学报. 2016, 39(5): 1-22.

[4] 余凯，贾磊，陈雨强，等. 深度学习的昨天、今天和明天[J]. 计算机研究与发展. 2013, 50(9): 1 799-1 804.

[5] 郭丽丽，丁世飞. 深度学习研究进展[J]. 计算机科学. 2015(5): 28-33.

[6] 刘建伟，刘媛，罗雄麟. 深度学习研究进展[J]. 计算机应用研究. 2014, 31(7): 1 921-1 930.

[7] 刘颖超，张纪元. 梯度下降法[J]. 南京理工大学学报. 1993, 68(2): 12-16.

[8] 同济大学数学系. 高等数学[M].7版.北京: 高等教育出版社, 2015.

[9] 任玉杰. 高等数学及其Matlab实现辅导[M]. 广州：中山大学出版社, 2013.

Matrix Representation of Derivative of Multivariate Vector Function and Its Application in Artificial Neural Network

Yang Diwei, Bian Jiawen, Zhang Yujie

(School of Mathematics and Physics, China University of Geosciences, Wuhan 430074, China)

In the report, based on the introduction of the matrix representation of partial derivative of multivariate vector function, the operating principle of gradient-descent algorithm and its application in artificial neural network were proposed. The effectiveness of gradient-descent algorithm was proved by a Matlab simulation.

artificial neural network; deep learning; gradient descent; matrix representation of partial derivative of multivariate function

2016-05-26

中国地质大学(武汉)本科教学工程(ZL201634)；实验室基金(GBL31513)

杨迪威(1980-)，男，湖北恩施人，讲师，博士，研究方向：机器学习与图像处理，E-mail: yangdw@cug.edu.cn

1004-1729(2016)04-0313-06

O 172

A DOl：10.15886/j.cnki.hdxbzkb.2016.0047