一类常微分方程的数值解法
2017-01-13薛雷
薛雷
(山东财经大学 东方学院, 山东 泰安 271000)

一类常微分方程的数值解法
薛雷
(山东财经大学 东方学院, 山东 泰安 271000)
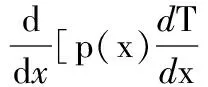
微分算子属于无界限性算子,在实际中得到了广泛的应用[1-6],特别是在工程、数学、物理等领域中应用更为广泛.微分算子理论中包括多种理论知识,如谱理论、自共轭扩张理论、数值计算、亏指数理论等.其中,谱理论在所有知识中又是最重要的,可以视其为核心.在数学界,微观粒子之间的作用一直是研究的热点问题,而Sturm-Liouville这一问题更是成为所有学者的研究焦点.Sturm-Liouville问题是二阶常微分方程分离变量求解方法的重要理论.徐有基[7]应用Leray-Schauder延拓定理,得到了二阶广义Sturm-Liouville边界条件多点边值问题的可解行.陈东晓等[8]研究了一类满足Sturm-Liouville积分边值条件的二阶非线性微分方程的正解性.基于以上研究,本文研究一类正则Sturm-Liouville微分方程的数值解.
1 预备知识
Sturm-Liouville方程为
上式中:p(x),q(x),ρ(x)在定义域内都是x的是函数,且p(x)>0,ρ(x)>0,q(x)>0.
在定义域范围内p(x),q(x)及p′(x)连续的.Sturm-Liouville方程齐边界条件可以归纳为
T(a)=T(b)=0,T′(a)=T′(b)=0,T(a)=T′(b)=0.
(1)
由式(1),可以求解Sturm-Liouville方程非零解.Sturm-Liouville的和复的边界条件为

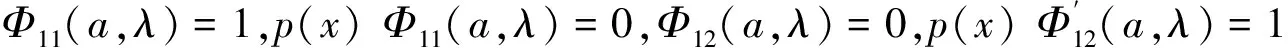
用Φ9和Φ22表示p(x) Φ11及p(x) Φ12.令Φ(x,λ)为Sturm-Liouville方程的解,有
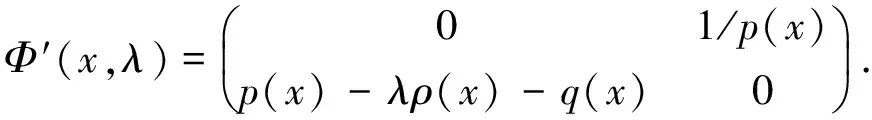
Sturm-Liouville方程的解可以化简为
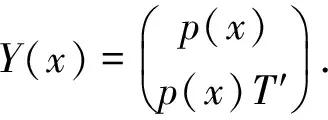
因此,边界条件可以形成AY(a)+BY(b)=0.分离边界条件可以表示为
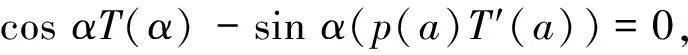

Y(x)可以用复数写为
Sturm-Liouville方程分离边界条件[9]为

上式中:a≤b,都为实数;α,β取值范围为[0,π].
2 一些引理及证明
关于Sturm-Liouville方程的完整性有如下3个引理.

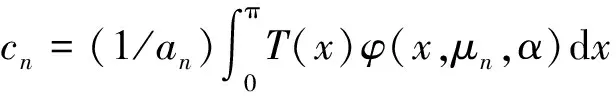
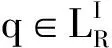
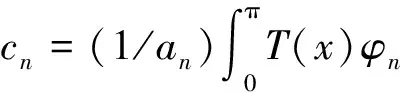
证明 当|λ|→∞时,渐近公式为
因此,估计值为
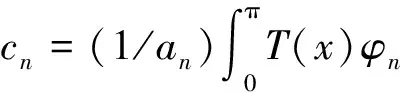
3 主要结果


当α=π,β=π时,有
an,bn的计算分别为

4 实际的应用



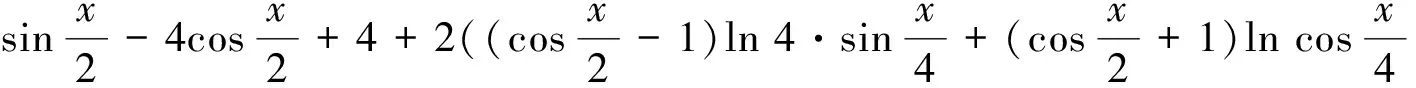


[1]BONHEURED,GOMESJM,HABETSP.Multiplepositivesolutionsofsuperlinearellipticproblemswithsign-changingweight[J].JournalofDifferentialEquations,2005,214(1):36-64.
[2]KHOLKINAM,ROFE-BEKETOVFS.Onspectrumofdifferentialoperatorwithblock-triangularmatrixcoefficients[J].JournalofMathematicalPhysicsAnalysisGeometry,2014,10(1):44-63.
[3]BASKAKOVAG,DIDENKOVB.Spectralanalysisofdifferentialoperatorswithunboundedperiodiccoefficients[J].DifferentialEquations,2015,51(3):325-341.
[4]GRUBBG.FractionalLaplaciansondomains,adevelopmentofHörmander′stheoryofμ-transmissionpseudodifferentialoperators[J].AdvancesinMathematics,2014,268(18):478-528.
[5]GRUBBG.Localandnonlocalboundaryconditionsforμ-transmissionandfractionalellipticpseudodifferentialoperators[J].Mathematics,2014,7(7):1649-1682.
[6]MIRONOVAE.Self-adjointcommutingordinarydifferentialoperators[J].InventionesMathematicae,2014,197(2):1-15.
[7] 徐有基.一类二阶广义Sturm-Liouville边界条件多点边值问题的可解性[J].西北师范大学学报(自然科学版),2008,44(4):1-5.
[8] 陈东晓,陈应生.二阶微分方程积分边值问题正解的存在性[J].华侨大学学报(自然科学版),2013,34(5):587-590.
[9]FELTRING,ZANOLINF.Existenceofpositivesolutionsinthesuperlinearcaseviacoincidencedegree:Theneumannandtheperiodicboundaryvalueproblems[J].AdvancesinDifferentialEquations,2015,20(9/10):937-982.
[10] HARUTYUNYAN T N.The dependence of the eigenvalues of the Sturm-Liouville problem on boundary conditions[J].Matematicki Vesnik,2008,60(4):285-294.
(责任编辑: 陈志贤 英文审校: 黄心中)
Numerical Solution for Class of Ordinary Differential Equations
XUE Lei
(Dongfang College, Shandong University of Finance and Economics, Taian 271000, China)

:Sturm-Liouvilledifferentialequation;boundaryvalue;positivesolution;differentialoperator
10.11830/ISSN.1000-5013.201701026
2016-12-05
薛雷(1982-),男,讲师,博士,主要从事微积分及经济数学的研究.E-mail:xue-xiao@163.com.
国家自然科学基金管理科学面上资助项目(70971014)
O
A
