40°～90°供热直埋折角弯管的数值分析

郭婷婷， 王飞， 王国伟， 雷勇刚

(太原理工大学 环境科学与工程学院， 山西 太原 030024)

40°～90°供热直埋折角弯管的数值分析

郭婷婷， 王飞， 王国伟， 雷勇刚

(太原理工大学 环境科学与工程学院， 山西 太原 030024)

利用ANSYS有限元软件进行数值模拟，分析弯管折角角度、曲率半径、管径、壁厚和循环工作温差对40°～90°供热直埋折角弯管应力的影响规律.根据计算结果绘制不同影响因素与折角弯管最大应力曲线图.结果表明：随着弯管折角角度、曲率半径、管径、壁厚的增加，弯管最大应力值呈递减趋势；随着循环温差的增加，弯管应力最大值逐渐增大. 关键词： 供热直埋； 折角弯管； 最大应力； 数值分析

供热直埋管道的折角弯管[1-2]是供热管线最薄弱的环节之一.然而，管线中折角的应力影响因素尚未被系统研究.崔孝秉[3]最先对小角度曲管进行有限元法分析，指出弯头附近直管因曲管弯曲的影响也产生环向变形和相应的环向应力.2009年，欧洲规范阐述了小角度折角的疲劳分析，提出不同循环温差下允许的最大小折角[4].吴玉国等[5]采用有限单元法对埋地输油管道的弯管进行分析，得出埋地输油管道弯管的应力随夹角和曲率半径的变化规律.文献[6-7]利用 ANSYS 有限元软件对L型弯管进行模拟分析，分析其应力变化规律，并将有限元解与弹性抗弯铰理论计算值进行比较，验证模型建立及荷载施加方法的合理性.文献[1]规定了可以当做直管段使用的最大允许折角(不大于4.3°).李明强[8]对折角为5°～40°的曲管在不同载荷下的应力大小及分布规律做了系统的分析和总结，指出曲管的主要失效形式.已有文献对40°～90°折角弯管的研究很少，但它们在实际工程中的应用却很多,所以有必要对40°～90°折角弯管的受力情况及影响因素进行分析.ANSYS是一款应用广泛的有限元分析软件.它集结构、热、流体、电磁、声学于一体，可以直观地实现复杂结构的受力分析[9]，具有电磁分析、接触分析、优化设计、结构高度非线性分析、自适应网格划分、大应变/有限转动等功能.鉴于ANSYS有限元软件在结构受力分析上出色的性能，本文采用ANSYS软件探讨40°～90°供热直埋折角弯管承载能力的影响因素.

1 数学模型

为了能用节点位移表示单元体的位移、应变和应力，在分析连续体时，必须对单元中唯一的分布做出一定的假设.假定位移是坐标的某种简单的函数，这种函数称为位移模式或位移函数(形函数)，即

(1)

式(1)中：u为单元内任意一点的位移列阵；N为形函数列阵；δe为单元节点位移列阵.

利用几何方程，由位移表达式导出用节点位移表示单元应变的关系式,即

(2)

式(2)中：ε是单元内任意一点的应变列阵;B为应变矩阵.

利用物理方程，由应变的表达式导出用节点位移表示单元应力的关系式,即

(3)

式(3)中：σ是单元内任意一点的应力列阵;D是单元材料有关的弹性矩阵.

利用虚功原理,建立作用于单元上的节点力和节点位移之间的关系式，即单元的刚度方程为

(4)

式(4)中：Ke为单元刚度阵;Re是单元上的节点力列阵.

计算相邻单元边界的等效节点力，集合所有单元的刚度方程，建立整个结构的平衡方程，求解节点的位移和计算单元应力，进行结构的有限元计算.

2 有限元模型的建立

2.1 物理模型

折角弯管示意图,如图1所示.图1中:φ为水平弯管的折角.文中研究的范围：折角φ为40°～90°(10°的步长)；两臂臂长l1,l2均取20m.折角弯管的实体采用20节点三维结构SOLID95单元.管道与土壤的耦合作用通过弹簧-阻尼单元模拟.弹簧-阻尼单元采用COMBIN14单元，其综合机床系数由保温层、膨胀垫块和土壤特性确定，根据文献[10]提供的方法计算.折角弯管的有限元模型,如图2所示.

图1 折角弯管示意图 图2 折角弯管有限元模型的网格划分Fig.1 Schematic diagram of angle elbow Fig.2 Grid division of finite element model of angle elbow

2.2 管道材料特性

管道材料特性(钢号Q235B)：杨氏弹性模量E=196 GPa；线膨胀系数α=12.6 μm·(m·℃)-1；泊松比γ=0.3；许用应力[σ]=125 MPa；屈服应力σs=235 MPa.

2.3 网格划分

采用自由划分的方式(图2),并进行网格独立性考核，以保证计算结果准确且节省计算资源.建立5套网格，对不同网格单元尺寸下的应力值进行计算，结果如表1所示.表1中：N为网格单元尺寸；σmax弯管应力最大值；η为相对减小量.由表1可知：随着网格单元尺寸的减小，即网格数的增多，弯管应力最大值整体呈下降趋势，但下降幅度较小，如网格单元尺寸从5 mm减小到4 mm时，弯管应力最大值仅减小0.885%.综合考虑准确性和节省资源，采用第3套网格进行数值模拟计算.

表1 网格独立性考核Tab.1 Grid independence test and verification

2.4 边界条件及施加荷载

图3 折角弯管应力云图Fig.3 Stress nephogram of angle elbow

弯管荷载包括力作用和变形作用两种形式.力作用主要由管内介质的压力引起，通过对管道内表面施加压力荷载实现.变形作用由管内介质的温度变化引起，通过对管道整体施加温度荷载完成.弯管两直臂端面的边界条件设置为轴向固定.施加全部荷载及边界条件后进行计算，结果如图3所示.

3 模拟与分析

目前，设计温度通常为130 ℃，设计压力已达2.5 MPa，管径也已达1 400 mm.因此，为了使研究和分析的成果更具有实用性和针对性，能够直接为40°～90°折角弯管的设计提供参考和借鉴，将分析的基础参数及管网工作参数界定在实际工程常用的范围内，即工作压力不大于2.5 MPa，循环最高温度为130 ℃，循环最低温度10 ℃，预制保温管为聚乙烯外护聚氨酯保温，土壤与高密度聚乙烯外护间的摩擦系数μmin=0.2，μmax=0.4，土壤的密度取ρ=1 800 kg·m-3.考虑到弯管曲率半径、壁厚、管径、温差等将会影响弯管的应力最大值，文中通过同一变量法，探究以上因素对弯管应力变化规律的影响.模拟工况说明，如表2所示.表2中：Rc为弯管的曲率半径；δ为壁厚；ΔT为循环工作温差；P为设计压力；H为直埋保温管管顶覆土深度；DN为管件的公称直径.模拟结果，如图4～8所示.

表2 模拟工况说明Tab.2 Explain of simulation conditions

图4 不同曲率半径下的σ-φ图Fig.4 σ-φ figure under different radius of curvature

3.1 弯管曲率半径对弯管应力最大值的影响

不同曲率半径下，弯管应力最大值(σ)-弯管折角角度(φ)图,如图4所示.由图4可知:随着弯管折角角度的增加，弯管应力最大值逐渐减小;在φ=50°处，出现拐点,即当φ<50°时，弯管应力值的减小速度小于φ>50°时弯管应力值的减小速度.同时，对折角为40°～90°的弯管随着曲率半径的增加，弯管应力最大值逐渐减小，而且弯管折角角度越大，弯管最大应力值减小的幅度越小.原因是当其他条件一定,曲率半径增大时，弯管的尺寸系数增大，导致弯管的应力加强系数减小，弯矩作用下的弯管应力会相应减小，最终导致弯管应力最大值减小，这与文献[11-12]的趋势一致，充分说明文中研究的正确性.当弯管折角角度为40°，60°，90°时，曲率半径从Rc=3DN增加到Rc=5DN，其应力最大值分别减小了26.7%，23%，10.2%.由此可以得出，对于40°～90° 供热直埋折角弯管来说，增大其曲率半径，可以有效提高弯管的承载能力.

3.2 弯管管径对弯管应力最大值的影响

不同管径下的σ-φ图，如图5所示.由图5可知：弯管应力最大值随弯管折角角度的增加呈递减形势；在φ=50°处，同样出现拐点.在相同的折角角度下，弯管管径越大，其最大应力值越小.原因是当其他条件一定、弯管管径增大时，弯管的应力加强系数和弯头断面的抗弯矩均增大，但抗弯矩增加的速度比应力加强系数增加的快，弯管应力会相应减小，最终导致弯管应力最大值减小，这与文献[11-12]的趋势一致.同时，增大管径时，折角角度φ<60°弯管的应力值减小的幅度大于φ>60°的弯管.

考虑到实际工程中DN800的管道壁厚为10 mm，DN1 200的管道壁厚为14 mm，做了另一组模拟. 模拟工况如下：设计压力2.5 MPa;ΔT=120 ℃;H=1.5 m;Rc=3DN. 对DN800-3DN-10 mm,DN1 000-3DN-12 mm,DN1 200-3DN-14 mm三种规格进行模拟，分别得出这三种工况下40°～90°折角的弯管应力值变化规律，结果如图6所示.图6中：DN800-3DN-10 mm表示弯管管径为DN800，Rc=3DN，δ=10 mm.

由图6可知：改变DN800，DN1 200的壁厚后，其规律与图5显示结果相似.一方面，弯管应力最大值随其折角角度的增加呈递减形势；另一方面，在相同的折角角度下，弯管管径越大，其最大应力值越小.但不同的是，对任一角度，当对弯管做出相同的规格调整后，其应力改变幅度相近.图6中：当管径从DN800增加到DN1 200时，φ=50°的弯管应力最大值减小了56 MPa，而φ=80°的弯管应力最大值减小了50 MPa.

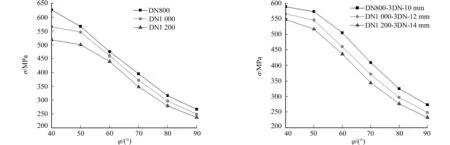
图5 不同管径下的σ-φ图 图6 不同规格下的σ-φ图 Fig.5 σ-φ figure under different pipe diameters Fig.6 σ-φ figure under different specifications

3.3 弯管壁厚对弯管应力最大值的影响

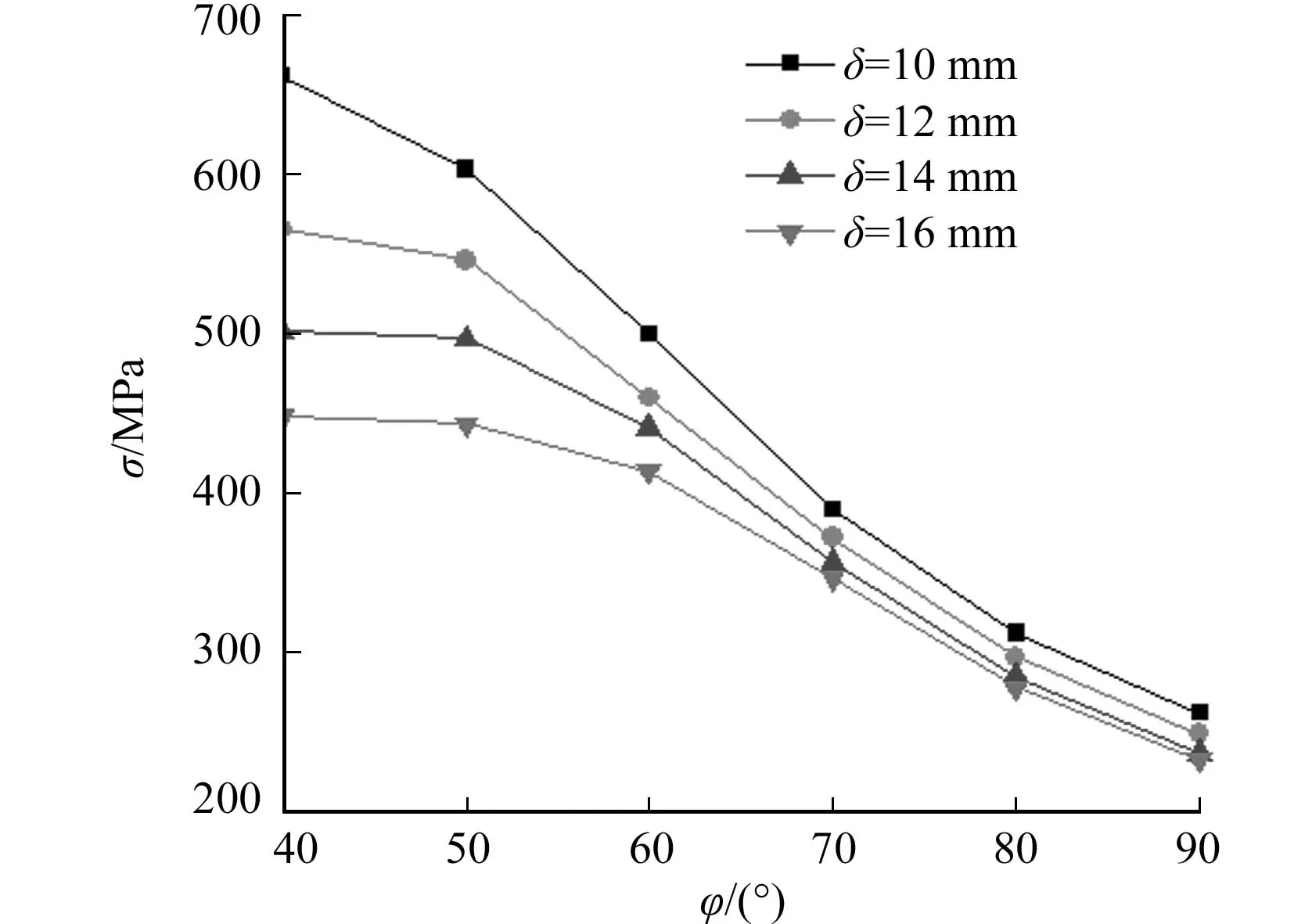
图7 不同壁厚下的σ-φ图Fig.7 σ-φ figure under different wall- thicknesses

不同壁厚下的σ-φ图，如图7所示.当φ=40°时，壁厚δ从10 mm增加到16 mm，最大应力值减小47.5%；当φ=60°时，壁厚δ从10 mm增加到16 mm，最大应力值减小了20.8%；当φ=90°时，壁厚δ从10 mm增加到16 mm，最大应力值减小了12.4%.由图7可知:在研究范围内， 弯管应力最大值随着折角角度φ的增加呈减小趋势，同样在φ=50°处，出现拐点.同时，随着弯管壁厚的增加，弯管应力最大值逐渐减小，且这种影响随着折角φ的增大而逐渐减弱. 其原因为：当其他条件一定，弯管壁厚增大时，弯管的应力加强系数减小，且弯头断面的抗弯矩增大， 这样弯管应力会相应减小，最终导致弯管应力最大值减小，这与文献[11-12]的趋势一致.

3.4 循环工作温差对弯管应力最大值的影响

图8 不同循环工作温差下的σ-φ图Fig.8 σ-φ figure under different temperature differences of cycle operation

不同循环工作温差下的σ-φ图，如图8所示.由图8可知：在文中的研究范围内，弯管最大应力值随折角角度的增加而减小.在相同弯管折角角度下，循环工作温差越大，弯管最大应力值越大.原因是其他条件一定,循环工作温差增加时，会使弯管轴向力增大，在其他条件相同的情况下，会导致更大的弯管最大应力值.当φ=50°时，循环工作温差为120 ℃的最大应力值为546 MPa；而循环工作温差为100 ℃的最大应力值为532 MPa.同时，循环工作温差对弯管最大应力值的影响，随折角角度变化不大.因此，对于高温管网的设计，更需注重水平弯管的承载能力.

4 结论

应用ANSYS有限元软件对40°～90°折角弯管进行数值模拟，研究了弯管的最大应力值在不同曲率半径、不同管径、不同壁厚、不同循环温差下，随着折角φ的变化规律，主要有以下4个结论.

1) 当40°≤φ≤90°时，随着折角φ的增加，水平弯管的补偿能力逐渐增强，弯管应力的最大值逐渐减小.

2) 当40°≤φ≤90°时，增加弯管的曲率半径，可以有效地提高弯管的承载能力.当40°≤φ≤60°时，改善效果尤为明显.

3) 增加管径会减小水平弯管的应力值.增加壁厚既可以提高管网强度，也可以降低水平弯管的应力值.然而，当折角φ>60°时，增加壁厚对弯管最大应力值的减小作用减弱.

4) 高温热水供热管网对水平弯管的强度要求更高，可以通过调整弯管曲率半径或者增加其壁厚降低弯管应力值，从而提高管网的安全性能.

[1] 城市建设研究院.城镇供热直埋热水管道技术规程: CJJ/T 81-2013[S].北京:中国建筑工业出版社,2013：14-15.

[2] 王飞,张建伟,王国伟,等.直埋供热管道工程设计[M].2版.北京：中国建筑工业出版社,2014:88-89.

[3] 崔孝秉.埋地长输管道纵向弯头温度内力的近似分析[J].华东石油学院学报，1980(2):46-56.

[4] British Standards Institution.Design calculation and installation for preinsulated bonded pipes for district heating: BS EN 13941-2009[S].London：Group B S I,2009:105-117.

[5] 吴玉国,周立峰,朱佳琦,等.埋地管道弯管应力数值计算[J].当代化工，2012，41(12):1406-1409.

[6] 王国伟.大口径供热直埋管道 90°弯头疲劳寿命的有限元分析[D].太原:太原理工大学,2010:73-75.

[7] 刘桢彬.直埋供热管道“L”形管段的受力分析[J].太原理工大学学报,2013,44(1):85-88.

[8] 李明强.大口径供热直埋热水管道曲管的研究[D].太原:太原理工大学,2015:44-58.

[9] 杨勇,郭子雄.大跨度石穹顶空间结构受力行为数值模拟[J].华侨大学学报(自然科学版),2005,26(3):267-270.

[10] RANDLOV P.区域供热手册[M] .贺平,等译.哈尔滨:哈尔滨工程大学出版社,1998:58-61.

[11] 贺平,孙刚,王飞,等.供热工程[M].4版.北京：中国建筑工业出版社,2009:354-355.

[12] 中华人民共和国国家发展和改革委员会.发电厂汽水管道应力计算技术规程: DL/T 5366-2014[S].北京：中国计划出版社,2014:26-29.

(责任编辑： 黄晓楠 英文审校： 方德平)

Numerical Analysis of 40°-90° Directly Buried Heating Angle Elbow

GUO Tingting, WANG Fei, WANG Guowei, LEI Yonggang

(School of Environment Science and Engineering, Taiyuan University of Technology, Taiyuan 030024， China)

ANSYS finite element software was used to carry out numerical simulation of 40°-90° directly buried heating angle elbow, which was to take analysis of how angle of the elbow, radius of curvature, pipe diameter, wall thickness and circulation work temperature influencing the stress of the elbow. The maximum stress curves were drawn to intuitively reflect the influences of all the factors on the bend stress. The results showed that, the increase of the bending angle, curvature, diameter and thickness of pipe led to a decreasing trend of the maximum bending stress; while widening difference in the cyclic temperature increased the maximum bending stress value of the elbow. Keywords： directly buried heating; angle elbow; maximum stress; numerical analysis

10.11830/ISSN.1000-5013.201701014

2016-01-30

王飞(1957-)，男，教授，博士，主要从事供热技术与节能的研究.E-mail:wfwfsir@126.com.

住房和城乡建设部科学技术计划项目(2016-K4-079)

TU 833.1

A

1000-5013(2017)01-0075-05