钢筋混凝土建筑结构的抗震性能分析与实验

郑睿, 于虹

(1. 长江工程职业技术学院 土木工程系， 湖北 武汉 430212;2. 华中科技大学 土木工程与力学学院， 湖北 武汉 430074)

钢筋混凝土建筑结构的抗震性能分析与实验

郑睿1, 于虹2

(1. 长江工程职业技术学院 土木工程系， 湖北 武汉 430212;2. 华中科技大学 土木工程与力学学院， 湖北 武汉 430074)

针对钢筋混凝土建筑结构展开了抗震性能研究，提出一种高适应性的Pushover分析方法.在传统Pushover方法基础上，充分考虑高阶振型和结构刚度蜕变的影响，通过补充设计提升抗震性能分析的适应性.为了有效应对地震中的不确定性，配置了3种载荷.实验结果表明：对于钢筋混凝土结构，在倒三角载荷、抛物线载荷及分层分布载荷下，可以从位移、角位移方面给出稳定的抗震性能分析. 关键词： 建筑结构; 抗震性能; 位移分析; 角位移分析； Pushover分析法

在我国规模不断扩大的城市中，高层建筑与超高层建筑大都以钢筋混凝土建筑结构为主，故钢筋混凝土建筑结构的抗震性能分析成为当下建筑行业关注的焦点[1-2].20世纪末期，基于承载力的抗震性能分析是普遍采用的理论方法[3].针对此项理论中的不足，季静等[4]进行了改进，建立了一种基于位移的抗震性能分析理论体系框架.董云菲[5]基于位移的抗震分析理论，注重对要分析的建筑实体进行结构分析，并从力学的角度分析震灾发生后建筑实体可能发生的弹性变形和塑性变形，从而具有了更高的实用性.Pan等[6]基于位移抗震性能的分析思想，将位移分析具体为结构总位移分析和层间相对位移分析，使得位移分析理论更加全面.时程分析是抗震性能实验分析的一种常见方法，综合考虑对惯性力、阻尼力、恢复力，构建有针对性的微分方程，进而从强度和变形两个角度分析地震发生时建筑结构的安全程度[7].在时程分析的基础上，如果突出地震震动时的加速度变化分析，就形成了增量动力学分析方法[8].Pushover方法从弹性性能和塑性性能的角度出发，分析建筑结构的抗震性能[9].当然，地震发生时在诸多方面存在不确定性，如地震震源、主震波发生的时刻、不同空间点位上的震动强度差异，都会影响到各种抗震性能分析方法的可靠性[10].本文在Pushover分析方法的基础上，改进提升其适应性，并通过3种不同地震载荷加载模式的配置提升抗震性能分析的可靠性.

1 3种地震载荷加载模式的配置

Pushover分析方法的基本原理是,构建地震发生时，建筑结构所受到的载荷情况.因此，合理的载荷模式配置，有利于提升Pushover分析方法的准确性.在分析建筑结构抗震性能时，地震过程中的诸多不确定性因素更是成为影响Pushover方法分析效果的最大障碍.往往建立起的一种载荷模式，对于一种情况下的抗震性能分析是合理的，但是对于另一种情况下的抗震性能分析则是不准确的，甚至是失效的.当地震发生时，为了尽可能覆盖载荷分布，在建筑结构的Pushover抗震分析中，配置3种载荷模式.其中，倒三角形态分布的载荷模式数学表达式为

(1)

式(1)中：n为建筑的总层数；gi为第i层建筑在垂直方向上的高度；gj为第j层建筑在垂直方向上的高度；zi为第i层建筑所受的重力载荷；zj为第j层建筑所受的重力载荷.

抛物线形态分布的载荷模式数学表达式为

(2)

式(2)中：λ为高阶震型的影响系数，其取值为

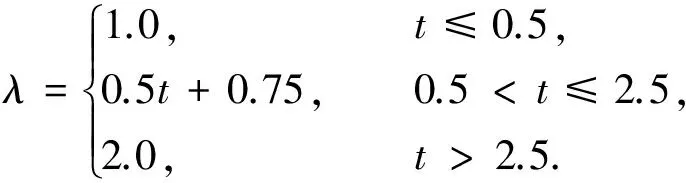
(3)

式(3)中：t为钢筋混凝土建筑结构的自振周期.

呈分层分布的幂级载荷模式数学表达式为

(4)

式(4)中： m为钢筋混凝土建筑结构的楼层序号，m=int(n/2)，int()表示取整处理.

2 高适应性Pushover抗震性能分析方法

在Pushover方法的抗震性能分析过程，对地震发生时的高阶震型影响、结构刚度蜕变等情况考虑得不够充分，因此，对不确定性较大的地震适应性较差.为此，建立一种高适应性的Pushover抗震性能分析方法.

用S表示建筑结构的侧向上的位移大小，用S0表示建筑结构的侧向上的名义位移大小，用θ表示施加载荷大小的参数.那么，3者之间的关系为

(5)

建筑结构的形状不尽相同，那么S0也会有所不同.但在实际进行分析时，为了分析过程的方便，对同一建筑结构的不同形状给予S0相同的取值.

(6)

式(6)中：i为建筑结构的楼层；j为建筑结构的第j阶震型；Θj为第j阶震型的参数；φi,j为第j阶震型的位移大小；ρj为第j个模态所对应的反应谱.

计算出各层间的位移SΔ，可进一步计算建筑结构各层的位移Si，即

(7)

计算出建筑结构全部楼层的位移大小之后，用maxSi表示其中的最大值，那么，可以对各个楼层的位移大小执行归一化处理，计算过程为

(8)

对于钢筋混凝土结构而言，如果结构反应达到一个峰值，那么，对应的载荷形状就会维持在稳定的状态.这时，即便载荷的数值大小发生变化，其形状也不会再改变.侧向载荷的更新处理为

(9)

3 实验结果与分析

用SAP 2000软件设置钢筋混凝土的浇注结构框架，共仿真设置了8层的建筑结构.底层的楼层高度设置为3.8 m，第2～8层的高度设置为2.8 m，楼层的边缘跨度为5.8 m，中间跨度为3.6 m.在边缘跨度上，梁的截面长度设置为50 cm、宽度为26 cm.楼体模型中，其他梁的截面长度设置为40 cm，宽度为26 cm.楼体模型中，柱子的截面长度和宽度都设置为45 cm.在建筑材料方面，梁和柱都设置二级钢筋配置C30混凝土的类型.

在地震波的仿真设置上，设定地震波的持续时间为30 s，仿真步长为0.03 s，地震波最大加速度为200 cm·s-2.

在3种载荷状态下，Pushover分析得到的楼层可允许的位移、楼层可允许的角位移，分别如图1，2所示.图1,2中：n为楼层；s为楼层位移；ω为楼层角位移.

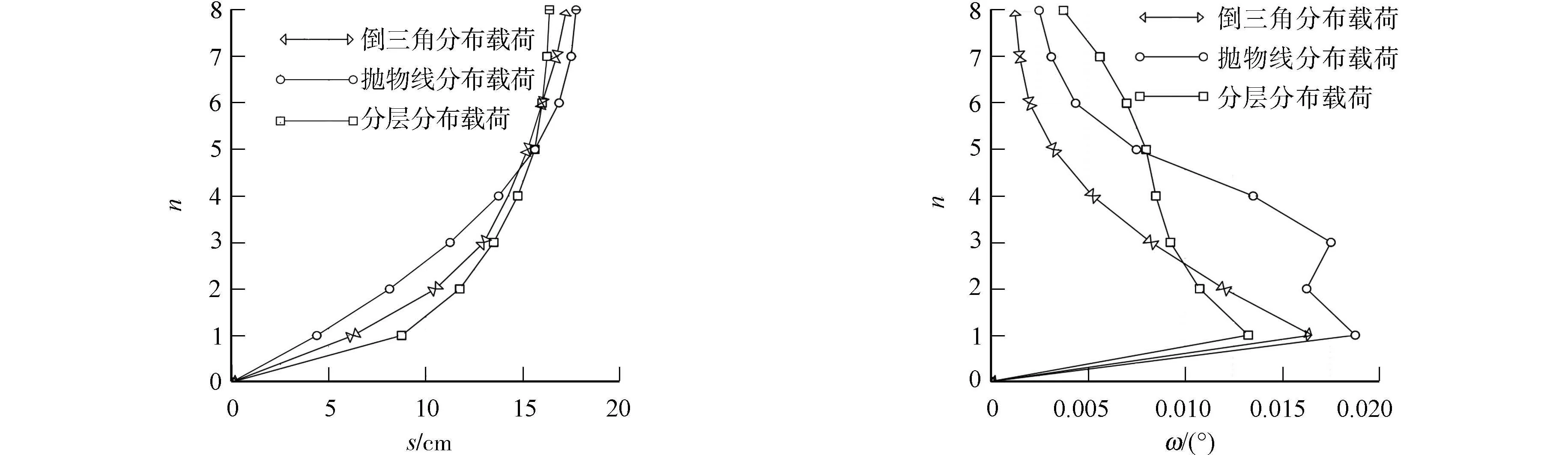
图1 楼层可允许的位移 图2 楼层可允许的角位移 Fig.1 Allowable displacement of floor Fig.2 Allowable angular displacement of floor

由图1可知：在倒三角形态分布载荷下，第1层楼的最大位移为6.8 cm，在抛物线形态分布载荷下，最大位移为4.5 cm，在分层分布载荷下，最大位移为8.2 cm；第8层楼的最大位移为17.4 cm，在抛物线形态分布载荷下，最大位移为17.8 cm，在分层分布载荷下，最大位移为16.8 cm.

由图2可知：在倒三角形态分布载荷下，第1层楼的最大角位移为0.016°，在抛物线形态分布载荷下，最大角位移为0.018°，在分层分布载荷下，最大角位移为0.013°；第8层楼的最大角位移为0.002°，在抛物线形态分布载荷下，最大角位移为0.003°，在分层分布载荷下，最大角位移为0.004°.

文中方法对于不同形态的载荷可以给出理想的分析结果，并且3种载荷的分析结果比较稳定.因此，文中方法在抗震性能分析具有较好的可靠性，对于地震发生时的不确定性，具有更好的处理能力.

4 结束语

面对不断扩建的城市和不断兴起的新型小区，提升其间高层建筑的抗震性能成为生命财产安全的重要保证.针对钢筋混凝土建筑结构的抗震性能分析问题，在Pushover分析方法的基础上进行了改进和补充，使之对地震中的不确定性具有更好的适应性.同时，配置了倒三角形态的载荷分布、抛物线形态的载荷分布、分层分布的幂级数载荷分布3种不同的载荷分布，更加全面地完成抗震性能分析.在3种形态的载荷分布情况下，Pushover分析方法对于钢筋混凝土结构的抗震性能分析具有很好的适应性.

[1] BLACK G,DAVIDSON R A,PEI S，etal.Empirical loss analysis to support definition of seismic performance objectives for woodframe buildings[J].Structural Safety,2010,32(3):209-219.

[2] 王曙光,陆伟东,刘伟庆,等.昆明新国际机场航站楼基础隔震设计及抗震性能分析[J].振动与冲击,2011,30(11):260-265.

[3] HAMID N H,MANDER J B.A comparative seismic performance between precast hollow core walls and conventional walls using incremental dynamic analysis[J].Arabian Journal for Science and Engineering,2012,37(7):1801-1815.

[4] 季静,陈学伟,何慧贤,等.基于概率和位移的框支剪力墙结构抗震性能评估方法[J].地震工程与工程振动,2009,29(6):108-114.

[5] 董云菲.考虑支座非载荷初始位移的超长复杂隔震结构抗震性能分析[D].兰州：兰州理工大学,2014：21-25.

[6] PAN Jiawen,YU Xi,FAN Jin.Ssismic performance assessment of arch dams using incremental nonlinear dynamic analysis[J].European Journal of Environmental and Civil Engineering,2015,19(3):305-326.

[7] JEHEL P,LEGER P,LBRAHIMDEGOVIC A.Initial versus tangent stiffness-based rayleigh damping in inelastic time history seismic analyses[J].Earthquake Engineering and Structural Dynamics,2014,43(3):467-484.

[8] VAMVATSIKOS D.stimating seismic performance uncertainty using IDA with progressive acelerogram-wise latin hypercube sampling[J].Journal of Structural Engineering,2014,140(8):657-670.

[9] 王瑜,陈震.建筑造型理论下景观构筑物的结构隐形作用[J].华侨大学学报(自然科学版),2015,36(1):97-102.

[10] 袁成,李景叶,陈小宏.基于概率统计的地震岩相识别不确定性定量评价方法[J].地球物理学报,2015,58(10):3825-3826.

(责任编辑： 陈志贤 英文审校： 方德平)

Seismic Performance Analysis and Experimental Study of Reinforced Concrete Building Structure

ZHENG Rui1， YU Hong2

(1. Department of Civil Engineering, Chang Jiang Institute of Technology, Wuhan 430212, China;2. School of Civil Engineering and Mechanics， Huazhong University of Science and Technology, Wuhan 430074, China)

The high adaptable Pushover analysis method is proposed to study the seismic behavior of reinforced concrete structures. This method is based on the traditional Pushover method, considering the effect of stiffness degradation and high order vibration modes, the seismic performance analysis of adaptability is improved by additional design. In order to effectively deal with the uncertainty in the earthquake, three kinds of load are distributed. The experimental results show that the seismic behavior of reinforced concrete structures can be analyzed according to the displacement and angular displacement under the inverted triangular load, the parabolic load and the stratified distribution load. Keywords： building structure; seismic performance; displacement analysis; angular displacement analysis； Pushover analysis

10.11830/ISSN.1000-5013.201701008

2016-11-25

郑睿(1974-)，男，高级工程师，主要从事建筑结构与施工技术的研究.E-mail:1691289966@qq.com.

国家自然科学基金资助项目(51078166)； 中国高等职业技术教育研究会资助项目(GZYLX201500)

TU 317

A

1000-5013(2017)01-0045-04