公路空间几何特性对汽车运动影响

葛 婷， 符锌砂， 李海峰， 龙立敦

(1. 华南理工大学 土木与交通学院, 广东 广州 510640； 2. 苏州科技大学 土木工程学院, 江苏 苏州 215011；3. 中南大学 地球科学与信息物理学院, 湖南 长沙 410007)

公路空间几何特性对汽车运动影响

葛 婷1,2， 符锌砂1， 李海峰3， 龙立敦1

(1. 华南理工大学 土木与交通学院, 广东 广州 510640； 2. 苏州科技大学 土木工程学院, 江苏 苏州 215011；3. 中南大学 地球科学与信息物理学院, 湖南 长沙 410007)

从三维的角度采用曲率、挠率代替传统平、纵线形设计参数对公路中心线的空间几何特性进行描述，并在Frenet标架的基础上，将汽车视为刚体，从微观角度建立了以三维线形指标曲率、挠率为控制量的汽车空间运动模型.结合已有设计资料，对公路线形的空间几何特性对汽车运动的影响进行了详细分析.研究发现曲率的设置对汽车行驶起主导作用，挠率的影响相对较小；传统路线设计方法忽略了平、纵线形的耦合使得组合线形的曲率、挠率的连续性存在不同程度的衰减，直接影响到行车运动状态的平稳变化和行车舒适性水平.

公路； 空间几何特性； 曲率； 挠率； Frenet标架； 运动学

汽车在道路上行驶时，驾驶员所关心的主要是车辆的加速、制动、转向方面的运行平稳性和行驶舒适性，在自由流条件下，这些运动特性主要受前方视野一定范围内的线形几何特性影响.传统公路几何设计将带状公路浓缩为一条空间曲线，分别对其平面和纵断面投影进行相应设计，然后组合形成中心线.关键线形设计参数如最小半径、最大纵坡等的确定仅考虑汽车单方向的行驶特性，忽略了其他方向的交互作用和对驾驶员生理、心理的影响，相应设计规范对线形组合也仅作了模糊规定，无法在实践中执行，使得汽车在曲线路段因失稳和操作不当而发生车祸的现象时有发生.随着公路运输向高速化、人性化的发展，线形条件对行车安全性及舒适性的影响愈加敏感.

近10多年来，各国学者逐渐意识到忽略公路三维线形本质对行车安全和舒适性所带来的严重影响，并尝试从三维角度对现行路线设计方法和交通安全进行改进和提高[1-3].公路线形设计要素与汽车运动特性的关系模型是公路线形设计的理论基础，也是关键几何线形指标确定的依据，目前相关学者主要从以下3个方面展开研究：一是根据路段实测数据统计回归建立线形几何要素与运行速度之间的关系模型，进而从宏观角度确定和分析线形几何要素变化对汽车运动特性和行车安全的影响，Misaghi等[4]对常用的运行速度预测模型进行了详细的总结和分析；二是通过对车辆模型适当简化，结合汽车运动学和动力学建立理论分析模型，如目前广泛使用的速度与圆曲线半径的关系模型即是将车辆假设为质点通过汽车平面转弯时的受力分析建立的[5]，国内一些学者还建立了可能运行速度预测模型[6]、理论运行速度模型[7]；三是借助于专业的软件，结合自身需求进行相应的模型设置，在此基础上对线形几何要素与汽车运动特性进行动态分析和评价[8].但上述研究均是建立在传统二维线形几何要素简单叠加的基础上，鲜有建立平、纵线型组合后的空间线形对汽车运动特性的影响分析，关于公路真三维线形设计和现有二维设计方法存在的具体不足仍待进一步研究.

为此，本文从公路本身是一条可供车辆及其使用者行驶的空间三维曲线这一本质入手，利用微分几何曲线论中的曲率、挠率代替二维平、纵线形设计指标对公路中心线的空间几何特性进行描述.在Frenet标架基础下结合新建的公路三维线形指标对汽车的空间运动进行分析，建立曲率、挠率与速度、加速度、急动度之间的关系模型.

1 公路空间几何特性描述指标

公路中心线数学上可表示为一条三维空间曲线r(l)=[x(l),y(l),z(l)]，其中参数l表示弧长，即桩号；x(l)，y(l)，z(l)为曲线上任一点的坐标函数.传统公路中心线通过不同平、纵线形单元组合得到，而平、纵线形单元又由不同的基本线形要素构成.取中心线上任一点P，该点位于第i个平面单元和第j个纵断面单元中，如图1所示，R为平曲线半径，α为方位角，kp为P点的平面曲率，lis和lie分别为第i个平面单元起、终点桩号，kpis和kpie分别是第i个平面单元起、终点平面曲率，ijs和ije分别为第j个纵断面单元起、终点纵坡，ljs和lje分别为第j个纵断面单元起、终点桩号.在平、纵线形中取相同微分单元dl，得P点坐标如下：

(1)

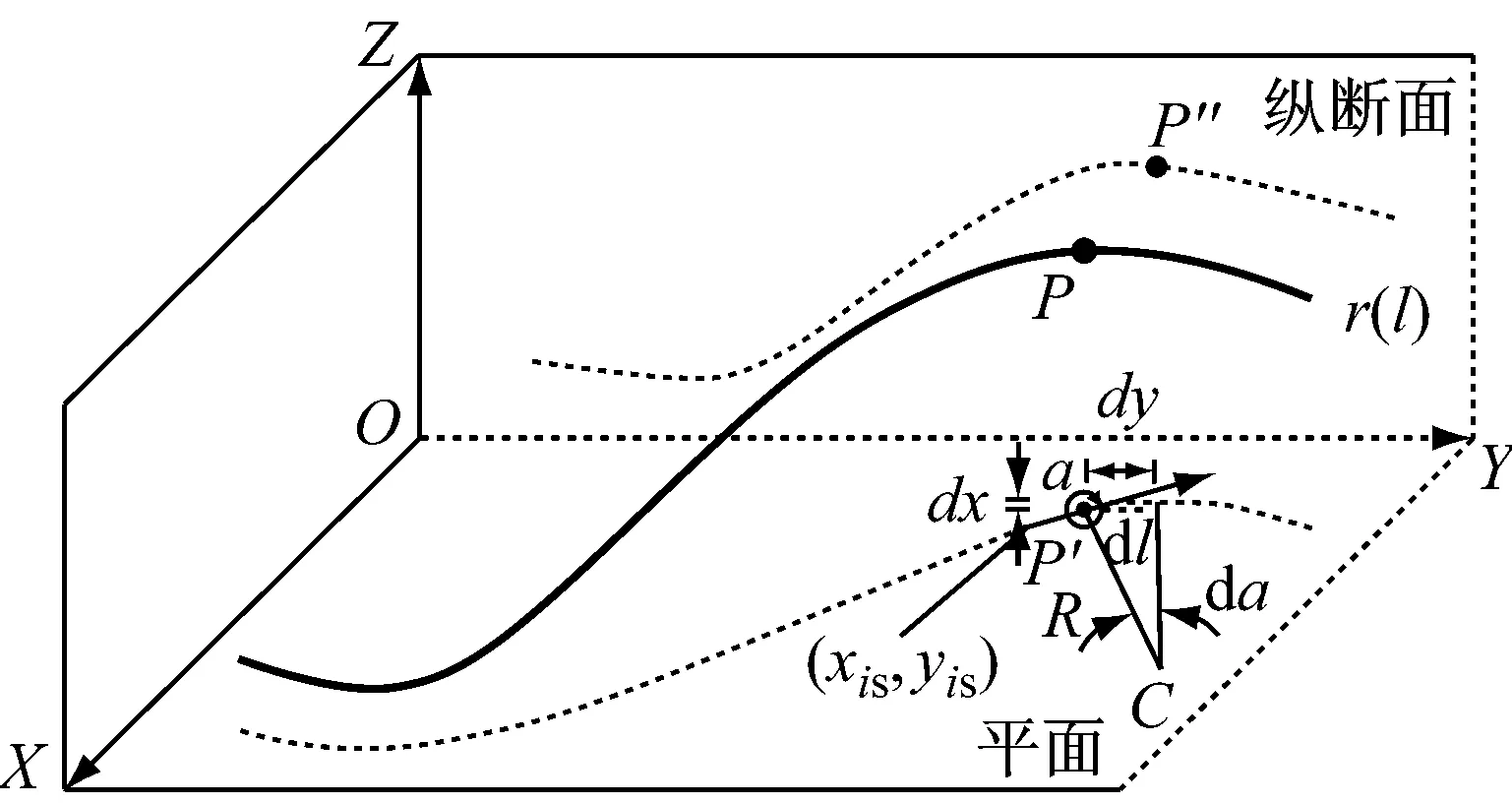
a 公路平、纵线形组合示意

b 第i单元平面线形及平面曲率

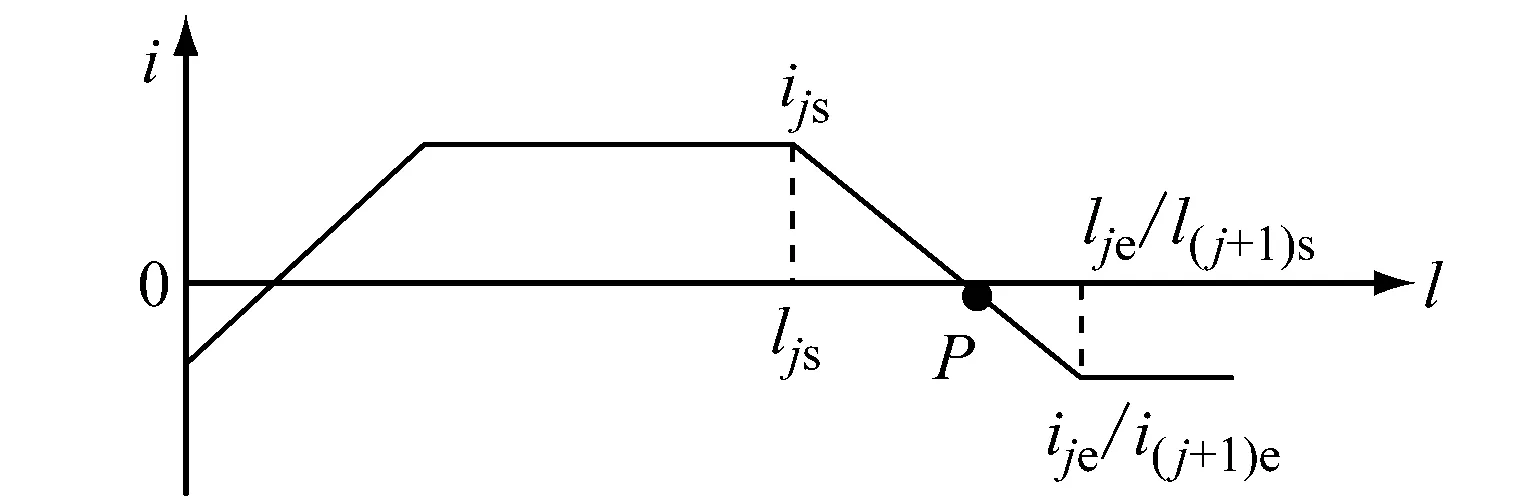
c 第j单元纵断面线形及坡度图1 公路线形示意Fig.1 Schematic diagram of highway alignment

二维平面曲线的形状完全由其平面曲率唯一决定，而纵断面线形主要由纵坡变化情况确定.但平、纵线形组合后的空间曲线的形状难以根据平面曲率和纵坡直观反映，两者之间的耦合效果无法量化.根据曲线论可知，三维曲线的空间走向和形状可完全由其基本几何不变量曲率和挠率确定.其中，曲率表示曲线弯曲的程度，挠率是刻画曲线空间弯曲状况的另一个重要的几何量，表示空间曲线相对于平面的扭转程度.故可将三维空间中的曲线理解为将一根直线通过弯曲(曲率)和扭转(挠率)得到[9]，见图2，其中，κ为曲率，τ为挠率.当挠率为零时，该曲线为二维平面内的曲线，其形状完全由曲率唯一决定.因此，本文采用曲率、挠率这2个三维线形指标代替传统二维线形参数来客观描述公路中心线的空间几何特性.根据微分几何，曲率和挠率的计算如下：

(2)

图2 空间曲线生成示意Fig.2 Generation of the spatial curves

将式(1)代入曲率和挠率计算公式中，可建立传统二维设计要素平面曲率、纵坡和三维线形指标曲率、挠率之间的关系模型，如式(3)所示：

(3)

2 汽车空间运动模型

为了准确地对汽车空间运动进行数学描述，必须建立适当的坐标系.图3为汽车的空间运动分析时所需的全局坐标系和车辆坐标系.全局坐标系为固定惯性坐标系OXYZ，位于路线起点，其3个方向的单位矢量分别为i，j，k.车辆坐标系为原点OC固定于车辆重心处，并随车辆一起移动的动坐标系OCXCYCZC，见图3，其中，3个坐标轴依次指向车辆前进方向、横向弯道一侧和垂直这2个方向构成的

竖向方向；α，β，γ分别对应车辆的侧倾角、俯仰角和横摆角.路线设计时假定汽车沿公路中心线行驶，则汽车重心轨迹在空间上与公路中心线相互平行，其线形构成数学上均可用r(l)进行描述.空间曲线上任意一点处可定义一个由单位切矢量T、单位主法矢量N和单位副法矢量B构成的Frenet标架[10].该Frenet标架与上述定义的车辆坐标系重合，各个方向的单位矢量如下：

(4)

研究分析时将汽车视作刚体，其空间运动由平移和旋转共6个自由度构成，分别为沿T方向的纵向移动、沿N方向的侧向移动、沿B方向的竖向运动，以及绕T轴的侧倾运动、绕N轴的俯仰运动和绕B轴的横摆运动(见图3).平移运动可由其重心在全局坐标系OXYZ中的位置矢量r(l)=[x,y,z]T表示；旋转运动可视为Frenet标架相对于全局坐标系的转动，采用旋转角[α,β,γ]表示.通过转换矩阵可将车辆运动从全局固定坐标系OXYZ转化至车辆坐标系OCXCYCZC中进行分析，见下式：

(5)

通过上述转换将汽车空间运动进行了简化分析，只需考虑汽车在车辆坐标系中的空间平移运动.理论上道路中心线可看成是汽车重心随时间变化的行驶轨迹，数学上可表示为一条三维空间曲线r(l)=[x(l),y(l),z(l)]T.在几何意义上，曲率表示曲线的单位切矢量对于弧长的旋转速度，挠率表示空间曲线的副法矢量相对于弧长的转动速度，则有

(6)

将式(4)中的T,N和B对l求导，结合式(6)，即可得到T，N，B三轴随弧长的变化情况，即Frenet-Serret公式[11]，如式(7)所示.

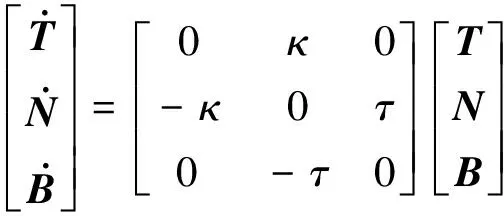
(7)

由此可知，当Frenet标架确定后，相应的旋转矩阵和旋转角也随之确定.Frenet标架和曲率、挠率一样是空间曲线的基本几何不变量，曲率、挠率可以完全确定一条空间曲线形状，而Frenet标架可以完整、唯一地表示沿空间曲线运动过程中状态方向的变化.故以Frenet标架为基础，将公路线形几何特性对汽车空间运动的影响分析转换为汽车重心轨迹随公路线形变化时相应的汽车运动状态的变化进行研究.数学上，曲线相对于路径参数的一阶导数是速度，二阶导数是加速度.结合Frenet标架，将r(l)对时间t求导，建立汽车运动指标与公路线形几何特征指标κ，τ和Frenet标架之间的关系模型，如下式所示：

图3 参考坐标系Fig.3 Reference coordinate system

(8)

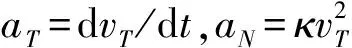
由此可知，公路线形几何特性对汽车行驶过程中各个方向的运动起主要控制作用.以侧向加速度和竖向急动度为例，当曲率为零时，空间上为一条直线，此时侧向加速度为零，不存在沿侧向移动的趋势；随着曲率增大，曲线弯曲越明显，产生的侧向加速度也越大(见图4a).当挠率为零时，空间上为一直线，此时不会产生竖向振动；当曲率、挠率均不为零时，汽车除会产生侧向运动的趋势外，还会产生沿竖向偏离平面运动的趋势，挠率绝对值越大，车偏离TN构成的密切面的旋转速度也越大(见图4b).即汽车空间运动变化并不是单个曲率或挠率的作用，而是两者耦合的作用.考虑到公路线形设计的需要，与平面曲率类似，引入正负号来反映空间曲率的弯曲方向，空间曲率小于零、大于零分别意味着沿切线方向前进时逆时针(向左)或顺时针(向右)转动.

a 侧向加速度

b 速率为100 km·h-1的竖向急动度图4 三维线形参数与汽车运动学指标之间的关系Fig.4 Relationship between 3-D geometric parameters and kinematics indexes

3 实例分析

为了明确传统公路线形空间几何特性对汽车运动特性的影响，本文以设计速度为100 km·h-1的某段公路为例进行研究分析，具体平、纵线形设计资料见图5，结合式(3)计算得到组合线形的曲率、挠率见图6.假定汽车分别以100，80，60 km·h-13种速度沿该路段行驶，可得到相应的运动学指标变化情况(以侧向加速度和竖向急动度为例)，如图7.

根据式(3)可知，公路线形空间几何特性的变化主要与平面曲率、纵坡及其变化率有关，平面、纵断面线形设计仅简单地满足了平面曲率、纵坡的连续，并没有保证平面曲率变化率、纵坡变化率的连续以及平纵线形组合后的空间曲线的几何连续性.由图6中椭圆标示出的部分路段可以明显看出二维设计和三维组合的不同，在二维平纵线形要素变化处，组合线形的空间曲率和挠率存在不同程度突变，空间线形的连续性存在不同程度的衰减.尤其当平面直线段直接与圆曲线段连接不设缓和曲线时，在直圆和圆直点处，曲率跳跃最为明显，见图6a椭圆标示出的K17+000～K18+000中间路段，这充分说明了现行道路设计方法在平面线形中增设缓和曲线不仅可以实现平面曲率的连续，还可以降低空间曲线曲率的突变量；但当缓和曲线与竖曲线组合时，在竖曲线要素变化处缓和曲线的过渡作用被削弱，曲率、挠率均存在明显的突变.由此可见，组合线形不是简单的平、纵叠加，线形组合的空间耦合效果可通过曲率和挠率进行合理评估和分析.

a 平面线形设计资料

b 纵断面线形设计资料图5 公路平、纵线形设计资料Fig.5 Horizontal and vertical alignments of highway

a 空间曲率

b 挠率图6 公路线形空间曲率与挠率Fig.6 Curvature and torsion of highway alignments

a vT=100 km·h-1时aN与l之间的关系

b vT=100 km·h-1时JB与l之间的关系

c vT=80 km·h-1时aN与l之间的关系

d vT=80 km·h-1时JB与l之间的关系

e vT=60 km·h-1时aN与l之间的关系

f vT=60 km·h-1时JB与l之间的关系图7 以不同速率行驶时的运动学指标变化情况Fig.7 Changes of vehicle kinematics indexes with different speeds

结合式(8)中的运动学模型可知，一条路径是否可供汽车稳定行驶主要由路径的曲率和挠率决定，其中曲率起主要控制作用，挠率主要影响车辆竖向急动度变化.传统设计方法建立的组合线形的曲率、挠率的不连续会直接影响到车辆的操作，使得侧向加速度和急动度也会产生急剧变化.目前国内外诸多学者均采用加速度及急动度作为行车安全与舒适性的评价指标，并对驾驶员行驶过程中所能忍受的最大加速度及急动度进行了详细的研究[12-13].根据已有实测数据和我国公、铁路线形设计中的一般规定，综合确定行车舒适性的运动学指标的阈值分别为：aN,com=1.0 m·s-2，jN,com=0.6 m·s-3，jB,com=0.24 m·s-3，其中，aN,com，jN,com，jB,com分别为侧向加速度、侧向急动度和竖向急动度舒适性阈值.由图7可知，当汽车以设计速度100 km·h-1稳定行驶时，K17+000处由于空间曲率过小，相应的侧向加速度超过了行车舒适性的阈值(图7a)，图6a椭圆标示出的K16+000和K17+500～K18+000中间路段曲率不连续，则该处的侧向加速度存在跳跃突变，使得侧向急动度远超0.6 m·s-3阈值；图7中竖向急动度虽未超过行车舒适性阈值，但由于K15+000和K16+000处挠率的突变，使得竖向急动度也产生了突变.力学上急动度的突变会形成冲击力，轻则影响行车舒适性，重则影响运动系统的稳定状态，对行车安全构成威胁[14-15].为保证行车安全和舒适，建议在K15+000～K17+500处需限速60 km·h-1.由此可见，现行路线设计方法忽略了平、纵线形空间耦合的影响，使得组合线形的曲率、挠率的连续性存在不同程度的衰减，并不能满足汽车稳定行驶和行车舒适的要求.

4 结语

从三维角度采用曲率、挠率描述公路组合线形的空间几何特性，研究发现传统平、纵线形设计方法并不能保证组合线形的连续性，在二维线形要素变化处，组合曲线的曲率和挠率存在不同程度的衰减.在Frenet标架基础上对汽车空间运动进行了分析，建立了三维线形指标曲率、挠率与汽车空间运动指标速度、加速度、急动度之间的关系模型，模型表明公路三维线形中的曲率对汽车空间运动状态起主导作用，挠率仅与竖向急动度变化有关.为保证汽车运行的平稳性，公路线形设计时应至少保证二阶几何连续，即曲率连续.结合已有道路数据发现传统平纵分离式路线设计方法并不能满足汽车稳定行驶和行车舒适性的要求，公路线形设计必须考虑线形的空间几何特性.建立的空间运动模型可为运营期局部路段限速值的确定以及后续公路真三维设计提供理论参考.

[1] 符锌砂,葛婷,李海峰,等.基于公路三维线形几何特性的行车安全分析[J].中国公路学报,2015,28(9):24.

FU Xinsha, GE Ting, LI Haifeng, et al. Traffic safety analysis based on geometric properties of highway three-dimensional alignment [J]. China Journal of Highway and Transport,2015,28(9):24.

[2] Jha M K, Karri G A K, Kühn W. Selection of 3D elements for different speeds in the 3D modeling of highways[C]∥The 4thInternational Symposium on Highway Geometric Design. Washington D C:Transportation Research Board,2010:1-17.

[3] Kühn W. The basics of a three-dimensional geometric design methodology[C]∥The 3rdInternational Symposium on Highway Geometric Design. Chicago: Transportation Research Board,2005:1-16.

[4] Misaghi P, Hassan Y, Asce M. Modeling operating speed and speed differential on two-lane rural roads[J] . Journal of Transportation Engineering,2005,131(6):408.

[5] American Association of State Highway and Transportation Officials. A policy on geometric design of highways and streets[S]. Washington D C:Federal Highway Administration, 2011.

[6] 杨少伟,石飞荣,潘兵宏,等.可能速度及其在公路线形设计中的应用方法[J].长安大学学报:自然科学版,2004,24(3): 1.

YANG Shaowei, SHI Feirong, PAN Binhong, et al. Application of possible velocity in design for highway alignment[J]. Journal of Chang’an University: Natural Science Edition,2004,24(3):1.

[7] 符锌砂,刘震.基于平纵组合线形的理论运行速度预测模型[J]. 长安大学学报:自然科学版,2010,30(3):24.

FU Xinsha, LIU Zhen. Prediction model of theoretical operating speed based on combination alignment of cross and vertical section[J]. Journal of Chang’an University: Natural Science Edition, 2010,30(3):24.

[8] 彭其渊,徐进,罗庆,等.公路平曲线参数对车辆轨迹和速度的影响规律[J].同济大学学报:自然科学版,2012,40(1):45.

PENG Qiyuan, XU Jin, LUO Qing, et al. Effect of horizontal curve design on track and speed of passenger car [J]. Jounal of Tongji University: Natural Science, 2012,40(1):45.

[9] Lipschutz M. Schaum’s outlines of differential geometry[M].New York: McGraw-Hill Eductaion,1969.

[10] Oprea J. Differential geometry and its applications[M]. Cambridge: Cambridge University Press, 2007.

[11] Farouki R T. Pythagorean-hodograph curves: Algebra and geometry inseparable[M]. Berlin: Springer Press, 2008.

[12] Hildebrand E D H D, Lewis J L. Driver tolerance of lateral accelerations on horizontal curves[J]. Canadian Journal of Civil Engineering, 2010, 37(3):413.

[13] 李运胜.高速环道几何线形的运动学评价[J].中国公路学报,2002,15(3):23.

LI Yunsheng. Kinematics appraisal on the geometric route of high-speed loop [J]. China Journal of Highway and Transport, 2002, 15(3):23.

[14] Schot S H. Jerks: The time rate of change of acceleration[J]. American Journal of Physics, 1978,46(46):1090.

[15] 刘筠,王剑华.加速度变化率对汽车制动器磨损特性的影响[J].长安大学学报:自然科学版,2007,27(6):95.

LIU Jun, WANG Jianhua. Effect of changing rate of accelerations on horizontal curves [J]. Journal of Chang’an University: Natural Science Edition,2007,27(6):95.

Influence of Spatial Geometric Properties of Highway Alignments on Vehicle Kinematics

GETing1,2,FUXinsha1,LIHaifeng3,LONGLidun1

(1. School of Civil Engineering and Transportation, South China University of Technology, Guangzhou 510640, China; 2. School of Civil Engineering, Suzhou University of Science and Technology, Suzhou 215011, China; 3. School of Geosciences and Info-Physics, Central South University, Changsha 410007, China)

Firstly, curvature and torsion instead of traditional two-dimensional (2-D) horizontal and vertical indexes were used to describe the spatial geometric properties of highway alignment according to the curve theory of differential geometry. Then the vehicle was treated as a rigid body and a new motion model was established with the curvature and torsion as the control variables base on the Frenet Frame. Finally, an example was analyzed to demonstrate the influence of spatial geometric properties of an existing highway on vehicle kinematics. It is found that the setting of curvature plays a leading role in the spatial motion, while the torsion affects the motion less. The coupling effects of horizontal and vertical alignments were ignored during traditional design process, which led to the continuity degradation of curvature and torsion, and directly affected the smooth variation of vehicle motion and driving comfort.

highway; spatial geometric properties； curvature; torsion; Frenet Frame; kinematics

2015-06-11

国家自然科学基金(51278202，51408229)

葛 婷(1987—),女,工学博士,主要研究方向为道路设计理论与方法、交通安全.E-mail:geting_happy@163.com

李海峰(1980—),男,副教授,工学博士,主要研究方向为道路设计理论与方法、三维GIS.E-mail:lihaifeng@csu.edu.cn

U412.3

A