流变岩体中支护圆形隧道施工过程的时效理论解
2017-01-13王华宁蒋明镜
王华宁, 宋 飞, 蒋明镜
(1. 同济大学 航空航天与力学学院, 上海 200092; 2. 山西省交通科学研究院 黄土地区公路建设与养护技术交通行业重点实验室, 山西 太原 030006; 3. 山西省交通科学研究院 黄土地区公路建设与养护技术山西省重点实验室, 山西 太原 030006; 4. 同济大学 土木工程学院, 上海 200092)
流变岩体中支护圆形隧道施工过程的时效理论解
王华宁1,2,3, 宋 飞1, 蒋明镜4
(1. 同济大学 航空航天与力学学院, 上海 200092; 2. 山西省交通科学研究院 黄土地区公路建设与养护技术交通行业重点实验室, 山西 太原 030006; 3. 山西省交通科学研究院 黄土地区公路建设与养护技术山西省重点实验室, 山西 太原 030006; 4. 同济大学 土木工程学院, 上海 200092)
针对水平和竖向地应力不相等的一般地应力条件下圆形隧道的断面开挖、纵向推进及衬砌施工问题,用任意黏弹性模型模拟不同岩石流变特性,用与时间相关的开挖函数模拟隧道断面开挖过程,用虚拟支护力等效纵向开挖效应,并在隧道开挖完成后的任意时刻施加弹性支护.采用复变函数方法和拉普拉斯变换技术给出用复位势表达的边界条件和围岩、衬砌接触位置协调条件,建立关于复位势中待定项系数的方程.通过求解方程确定待定项系数,从而得到开挖与支护整个施工过程任意时刻围岩位移和应力理论解答,并与相同条件下有限元解进行了对比.根据解答分析了围岩位移和应力的分布规律以及衬砌施加时刻对围岩位移和应力的影响.根据现有解析程序,可以形成快速预测隧道施工力学状态的计算机系统,方便、快捷地进行相似工程条件下的初步设计.
隧道; 支护; 黏弹性; 施工过程; 理论解
地下工程施工是一个长期过程,当考虑岩土体流变特性时,流变时效和施工过程叠加,使围岩和支护结构的力学状态与时间相关,因此,隧道设计中需要考虑施工过程和岩土体时效特性,以便合理预测并控制围岩位移与应力.圆形断面隧道无论在TBM (Tunnel Boring Machine)工法还是钻爆法施工中都最为常见[1];任意形状的非圆形隧道也可近似等效为圆形截面进行初步计算[2].解析方法可以用于工程初步设计,方便、快捷地计算全域各点的应力、位移,揭示各参量的内在机理,并可检验数值计算的正确性[3].
在支护深埋圆形洞室问题的理论分析中,Savin[4]给出单向拉伸情况下无限平板弹性支护与孔口完全接触和光滑接触情况下的应力弹性解.蒋斌松[5]针对空间轴对称衬砌结构和荷载的情形给出了考虑地下衬砌分段施工弹性问题的解析解.为考虑施加衬砌前围岩已发生的位移,Li等[6-7]引入与围岩半径相关的系数ε,利用复变函数方法给出带内压支护圆形压力隧洞应力和位移弹性解.Lu等[8]引入围岩位移释放系数η,用复变函数方法推导出双向不等压、带衬砌的弹性理论解答.当考虑掌子面纵向推进效应,Carranza-Torres等[9]引入释放系数fR,推导出双向不等压情况下围岩与衬砌完全接触和光滑接触2种情况的弹性解.
对黏弹性问题,理论解大多针对水平和竖向地应力相等的轴对称情况.Sulem等[10]将围岩模拟为Kelvin-Voigt模型,给出支护隧道支护力和位移的解析解.当考虑隧道纵向施工空间效应时,刘保国等[11]将释放荷载看成时间的函数,将围岩和衬砌模拟为黏弹性材料,用拉普拉斯变化法推演了均匀地应力下圆形洞室围岩与支护之间相互作用的时效规律.Fahimifar等[12]通过引入λ系数模拟掌子面的影响,用Burgers模型模拟岩石蠕变,推得随时间变化的围岩位移和应力.Nomikos等[13]考虑衬砌施加时刻,将围岩模拟为Burgers黏弹性体,给出轴对称情况下支护隧道位移和支护力的理论解.在实际工程中,隧道断面开挖并非一次成型.当考虑施工顺序时,王华宁等[14-15]针对黏弹性岩体中单层和双层支护圆形隧洞的施工问题,利用拉普拉斯变换和逆变换给出考虑施工顺序时轴对称问题的黏弹性理论解.以上轴对称问题的求解相对简单,但实际中水平和竖向地应力不一定相等(双向不等压),此时径向支护力随角度不再是定值,一般情况下存在切向支护力,且两者均为时间的函数,求解复杂.对双向不等压支护圆形洞室问题,焦春茂等[16]认为支护前隧道孔边只有弹性变形,用积分算子法得到黏弹性与弹性解的对应关系,并利用该关系得到围岩应力和位移黏弹性理论解.卞跃威等[17]考虑掌子面纵向推进效应,利用支护隧洞的弹性解和对应原理得到黏弹性解析解.以上研究中没有考虑断面开挖过程.对大断面的隧洞,除存在垂直于断面的纵向开挖(掌子面的推进),断面也非一次成型.钻爆法常采用断面分部开挖,而TBM施工可采用分次扩孔的方式.当隧道断面逐步开挖时,边界随时间变化,不可以直接应用对应关系进行求解.
本文在前期研究[14-15]基础上,尝试导出水平和竖向地应力不相等的一般地应力条件下黏弹性岩体中圆形隧道开挖和支护过程中应力、位移的理论解答.在推导中隧道为先受力、后开挖,考虑了任意纵向推进速度、任意时刻施加衬砌和断面的扩孔式开挖过程,并采用任意黏弹性模型模拟不同岩石的黏弹性流变特性.
1 力学模型
在针对黏弹性岩体中圆形隧道施工力学分析的理论推导中,为避免在数学上求解的困难,必须对实际情况进行一定简化,假定:①深埋隧道,可忽略重力梯度效应[18];竖向和水平向地应力分别为p0,λp0,其中λ为侧压力系数.②围岩为均匀、各向同性黏弹性材料.图1给出3种常用黏弹性模型,可以模拟不同类型岩石在不同应力水平下的流变特性,例如广义开尔文模型可以模拟在较低应力水平下岩石的稳态蠕变阶段.其中GH,GK为不同弹性元件的剪切模量;ηH,ηK为不同黏性元件的黏性系数.③衬砌处于弹性阶段.④隧洞断面在t=0时刻开始开挖,用开挖函数Rd(t)表征断面的任意开挖过程.开挖函数Rd(t)选用如下形式:
(1)
式中:t为时间(t=0为隧道开挖时刻);t0为开挖完成时刻;R(t)为根据断面开挖过程确定的函数;R1为开挖完成后洞口的半径.若t0=0则表示断面瞬时开挖完毕,即R(t)=R1.开挖完毕后t=t1时刻施加衬砌.⑤在实际施工中,纵向并非一次成型,受掌子面空间效应的影响,简化为平面问题时,可以认为作用在研究断面上的释放荷载与纵向推进过程相关[11].为避免考虑纵向开挖(掌子面推进)时三维计算的困难,用作用在研究截面内边界的虚拟支护力σr,f(t)和σrθ,f(t)等效纵向推进的三维效应[9]:
(2)


a麦克斯维尔模型b开尔文模型c广义开尔文模型
图1 黏弹性模型
Fig.1 Viscoelastic physical models
所以可以将该问题简化为平面应变问题,力学模型和坐标系如图2所示.对存在剪切地应力情况,可认为其主应力为p0,λp0,将本文中坐标轴转至主方向,则文中解答也可适用.衬砌厚度d=R1-R2.理论推导中符号规定与弹性力学相同,即拉应力为正,与极坐标方向一致的位移为正.

图2 力学模型Fig.2 Mechanical model
2 黏弹性问题应力与位移的复位势表达
采用复变函数理论结合拉普拉斯变换技术进行黏弹性问题求解.若φ(k)和ψ(k)为第k组外载对应的2个黏弹性复位势,文献[19]对应力边值问题给出黏弹位移(ux,(k)v和uy,(k)v)、应力(σx,(k)v,σy,(k)v和σxy,(k)v)与复位势φ(k),ψ(k)的关系如下:

(3)
(4)


表1 剪切松弛模量Tab.1 Shear relaxation moduli for the viscoelastic models
假设l组外载分别在t=tb1,tb2,…,tbl时刻开始作用于结构,并分别在t=tm1,tm2,…,tml时刻移除,根据黏弹性问题叠加原理[20]和卷积的拉普拉斯变换性质,t(t≥tbl)时刻的总响应为之前所有荷载分别作用于结构而引发的在t时刻响应的叠加,由式(3)得总位移(ux,v和uy,v)为

(5)
其中
(6)
由式(4)得增量应力(σx,v,σy,v和σxy,v)为
(7)
3 施工全过程力学状态的求解
3.1 隧洞开挖阶段的位移与应力
衬砌施加之前(0≤t (8) (9) 由黏弹性问题叠加关系,式(8)叠加支护力作用下围岩的位移解答可用于支护阶段围岩的位移计算,式(9)叠加支护力作用下围岩的应力解答可用于支护阶段围岩的应力计算. 3.2 支护阶段围岩、衬砌位移与应力的复位势表达 施加衬砌后,由于围岩与衬砌间的相互作用将在接触处产生支护面力.设该面力单独作用于围岩洞口时围岩对应的复位势为φR和ψR;而单独作用于衬砌结构时衬砌对应的复位势为φS和ψS.根据问题性质,可以用罗朗级数表示如上4个复位势[8]. 围岩对应的复位势为 (10) 衬砌对应的复位势为 (11) 式中:ak,bk,ck,dk,ek,fk(k=1,2,3,…,∞)为与时间相关的待定系数.因为衬砌在t=t1时刻才施加,所以引入新时间变量t′=t-t1表达以上复位势.由于衬砌尚处弹性阶段,根据复变函数理论可得衬砌位移和应力的表达式(t′≥0,即t≥t1). 位移为 uSr(z,t′)+iuSθ(z,t′)= (12) 应力为 (13) 式中:GS,KS分别为衬砌的剪切和体积模量.此阶段围岩受地应力和支护面力2组荷载作用,根据式(5),围岩位移可叠加得到: uRr(z,t)+iuRθ(z,t)=uRr,(1)(z,t)+uRr,(2)(z,t′)+ (14) 其中 (15) 为支护面力单独作用时产生的围岩位移.由于支护作用,围岩产生的增量应力为 (16) 支护阶段围岩应力σRr与σRθ即为式(9)、式(16)的叠加.分析可知,只要得到式(10)、式(11)中的待定系数,即可获得围岩和衬砌在支护阶段的应力和位移场.本文根据边界条件和协调条件进行复位势系数求解. 3.3 复位势系数的确定 (17) (18) 位移协调条件为 (19) 将式(14)、式(8)、式(12)代入式(19)可得用复位势表达的位移协调条件.式(19)含有卷积积分不易求解,且含有t,t′ 2个时间变量.为得到关于待定系数的代数方程,将所有时间变量统一为t′,然后针对t′对边界条件式(17)、式(18)和协调条件式(19)进行拉普拉斯变换.利用卷积拉普拉斯变换的性质,式(19)处理后的结果为 (20) (21) 将式(10)、式(11)代入式(17)、式(18)并进行拉普拉斯变换可得关于复位势待定项系数的另外2个方程: (22) (23) 令式(21)、式(22)、式(23)等式两边ekiθ项系数相等(k=-∞,…,+∞),可以得到一系列关于复位势待定项系数拉普拉斯变换量的代数方程. 通过式(21)两边ekiθ项系数相等(k=-∞,…,+∞)可得如下等式.对于e0有 (24) 对于eiθ有 (25) 对于e2iθ有 (26) 对于e3iθ有 (27) 对于e(k+2)iθ(k≥2)有 (28) 对于e-iθ有 (29) 对于e-kiθ(k≥2)有 (30) 通过式(22)两边ekiθ项系数相等(k=-∞,…,+∞),对于e0有 (31) 对于eiθ有 (32) 对于e2iθ有 (33) 对于e(k+2)iθ(k≥1)有 (34) 对于e-kiθ(k≥1)有 (35) 通过式(23)两边ekiθ项系数相等(k=-∞,…,+∞),对于e0有 (36) 对于eiθ有 (37) 对于e(k+1)iθ(k≥1)有 (38) 对于e-iθ有 (39) 对于e(-k-1)iθ(k≥1)有 (40) 3.4 解的退化验证 (41) 为检验本文理论和解答的正确性,利用有限元软件ANSYS进行与理论解相同模型下的计算,将结果与理论解答进行对比.在埋深300 m左右开挖一圆形洞室,围岩主要为泥岩和砂岩,重度γ=26.3 kN·m-3.根据埋深计算得到p0=7.89 MPa,侧压力系数λ=0.65[22].围岩采用广义开尔文模型(图1c),根据反分析可得岩石参数:GH=550 MPa,GK=458 MPa,ηK=4 000 MPa·d[23].衬砌为混凝土材料,剪切模量为GS=10 000 MPa,泊松比μS=0.2.隧道断面采用两次扩孔开挖方式,初始洞型半径R0=1 m(t=0),最终洞型半径R1=6 m(t=t0=2 d),即式(1)中的Rd(t)为: (42) 支护厚度d=300 mm,即R2=5.7 m.忽略三维效应的影响.ANSYS软件计算时,取第5天施加衬砌,通过复制面命令建立衬砌区域,提取围岩与衬砌接触处的节点坐标编号得到节点坐标并将接触处节点进行x,y方向位移耦合;在求解过程中,通过单元的生死命令模拟隧道开挖和施加衬砌的过程,由于建模时程序中设定了节点位移耦合,所以在激活衬砌单元的时候围岩位移不会出现反弹现象. 由于结构几何和受力均是上下和左右对称,数值计算时取结构的1/4,约束下边界竖向位移和左边界水平位移.计算范围和有限元网格如图3所示.图4给出围岩与衬砌接触位置0°,45°和90°处的位移和应力时程对比,其中ux,uy分别表示x,y方向的位移;σx,σy,σxy分别表示x,y方向的正应力和切应力.图4中解析解与有限元解位移量相对误差最大值为:1.24 mm,应力绝对误差最大值为0.256 MPa,误差较小,表明解析解答正确.相比数值解,解析解能方便地更改几何与物理参数,在应用于初步设计中更为有效. 图3 有限元计算模型及网格(单位:m)Fig.3 Model and mesh in FEM simulation (unit: m) a 位移 b 应力图4 隧道孔口位置点处位移和应力的有限元比较Fig.4 Comparison between analytical and FEM results on displacements and stresses for the points on the tunnel boundary 为进一步研究隧道开挖和支护整个施工过程的位移、应力的变化规律,现取一算例进行分析.岩石和衬砌参数、断面开挖方式与第4节相同.隧道纵向推进速率取vl=4 m·d-1.为与工程惯用符号一致,算例中位移和应力均与公式中符号相反,即:指向洞心位移位正;压应力为正.算例分析中的位移为开挖后的增量位移;应力为全应力. 5.1 衬砌施加时刻对位移、应力分布的影响 取4种衬砌施加时刻:①t1=2 d,即挖完立即支护;②t1=5 d;③t1=10 d;④t1=20 d.图5、图6分别给出位移基本稳定时刻(t=65 d),围岩与衬砌接触位置(r=6 m)处的位移与应力分布图.图5可看出,围岩径向位移从0°到90°逐渐增大,环向位移先增大后减小,其中在45°处达到最大,径向位移的总体量值比环向位移大.图6可看出,围岩径向和环向正应力随角度增大而减小,其中环向正应力数值较大,量值变化更剧烈,而径向正应力随角度变化非常平缓.围岩切应力随角度先增大后减小,在45°处达到最大,但总体量值不大.从图5、图6可看出,在不同衬砌施加时刻,围岩位移和应力分布形态大致相同,但衬砌施加越早,围岩位移越小,围岩与衬砌接触处径向正应力和切应力越大,而环向正应力越小,即围岩处于更安全的状态.对于本文算例,在不同衬砌施加时刻,稳定后围岩位移的差别为30%左右;而径、环向正应力量值差别接近,即从比例上讲,初砌施加时刻对径向正应力影响更加明显. a 径向位移 b 环向位移图5 隧道内边界处位移在不同衬砌施加时刻随角度的变化Fig.5 Displacements on the tunnel boundary versus the angle at four installation times a 径向正应力 b 环向正应力 c 切应力图6 隧道内边界处应力在不同衬砌施加时刻随角度的变化Fig.6 Stresses on the tunnel boundary versus the angle at four installation times 5.2 衬砌施加时刻对位移、应力时程变化的影响 仍取上述4种衬砌施加时刻,图7、图8给出4种情况在围岩与衬砌接触位置θ=45°处的位移与应力时程.从图7可看出,第1次扩孔该处位移很小,第2次扩孔后围岩位移在施加衬砌前迅速增大,施加衬砌后增长速度明显减缓.施加衬砌时刻越早,施加衬砌后围岩位移需更长时间才能达到稳定.图8为围岩应力时程图.该处径向正应力和切应力第1次扩孔后较大,第2次扩孔后瞬间减少,施加衬砌之后均逐渐增大;环向正应力第1次扩孔后较小,第2次扩孔后瞬间增大,施加衬砌后逐渐减小,最后均趋于稳定;由于纵向推进的影响,围岩受到虚拟支护力作用,所以施加衬砌前围岩径向正应力和切应力并不等于零,同时环向正应力也表现出渐变形态,5 d之后,即与掌子面距离大于20 m,纵向推进基本不再产生影响.衬砌施加时刻越早,各应力至稳定所需要时间越长.解答可以给出整个施工过程中围岩任意位置位移和应力随时间变化,用以预测并控制围岩的位移,特别是施加初砌后围岩的位移量;可以明确各点应力路径. a 径向位移 b 环向位移图7 不同衬砌施加时刻隧道内边界θ=45°处位移随时间的变化Fig.7 Displacements versus time on the tunnel boundary (θ=45°) at different liner installation times a 径向正应力 b 环向正应力 c 切应力图8 不同衬砌施加时刻隧道内边界θ=45°处应力随时间的变化Fig.8 Stresses versus time on the tunnel boundary (θ=45°) at different liner installation times 利用平面弹性复变函数方法和拉普拉斯变换,考虑隧道纵向推进的影响,推导了水平和竖向地应力不相等的一般地应力条件下黏弹性岩体中圆形隧洞开挖和支护过程的理论解答.给出的解答可适用于任何黏弹性模型的岩体、任意纵向推进速度和扩孔式开挖方式、任意时刻施加初砌的情况.位移、应力解答与相同模型的有限元解答进行对比,误差较小.对某地下隧道施工模拟分析表明:加初砌后的径向位移随时间呈指数形式增长且最终稳定于某一数值,不同衬砌施加时刻围岩位移、应力的分布和形态大致相同,衬砌施加时刻越早,支护力越大,相应稳定后的围岩位移量越小,但所需稳定时间越长.衬砌施加时刻对围岩与衬砌接触位置的径向正应力影响更明显,不同衬砌施加时刻稳定后位移的差别为30%左右.通过本文解答可以得到整个施工过程中各点位移、应力随时间变化关系. [1] 刘泉声, 黄兴, 时凯, 等. 煤矿超千米深部全断面岩石巷道掘进机的提出及关键岩石力学问题[J]. 煤炭学报, 2012, 37(12): 2006. LIU Quansheng, HUANG Xin, SHI Kai,etal. Utilization of full face roadway boring machine in coal mines deeper than 1 000 km and the key rock mechanics problems[J]. Journal of China Coal Society, 2012, 37(12):2006. [2] 李培楠, 刘俊, 苏锋, 等. 任意形状隧道围岩应力与位移的解析延拓求解[J]. 同济大学学报:自然科学版, 2013, 41(1):1483. LI Peinan, LIU Jun, SU Feng,etal. Analytical continuation method for solving stress and displacement of surrounding rock buried tunnel excavation with arbitrary shape section[J]. Journal of Tongji University: Natural Science, 2013, 41(1):1483. [3] Carranza-Tores C, Fairhurst C. The elasto-plastic response of underground excavations in rock masses that satisfy the Hoek-Brown failure criterion[J]. International Journal of Rock Mechanics and Mining Science and Geomechanics Abstract, 1999, 36(99): 777. [4] Savin G N. Stress concentration around holes[M]. London: Pergamon Press, 1961. [5] 蒋斌松. 地下衬砌的变几何应力分析[J]. 岩土工程学报, 1999, 1(1): 44. JIANG Binsong. On stress analysis of geometrically altered underground structures[J]. Chinese Journal of Geotechnical Engineering, 1999, 1(1):44. [6] Li S C, Wang M B. An elastic stress-displacement solution for a lined tunnel at great depth[J]. International Journal of Rock Mechanics & Mining Sciences, 2008, 45(4): 486. [7] Wang M B, Li S C. A complex variable solution for stress and displacement field around a lined circular tunnel at great depth[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2009, 33(3): 939. [8] Lu A Z, Zhang L, Zhang N. Analytic stress solutions for a circular pressure tunnel at pressure and great depth including support delay[J]. International Journal of Rock Mechanics & Mining Sciences, 2011, 8(3): 514. [9] Carranza-Torres C, Rysdahl B, Kasim M. On the elastic analysis of a circular lined tunnel considering the delayed installation of the support[J]. International Journal of Rock Mechanics & Mining Sciences, 2013, 61(10): 57. [10] Sulem J, Panet M, Guenot A. An analytical solution for time-dependent displacements in a circular tunnel[J]. International Journal of Rock Mechanics & Mining Sciences &Geomechanics Abstracts, 1987, 24(87): 155. [11] 刘保国, 杜学东. 圆形洞室围岩与结构相互作用的黏弹性解析[J]. 岩石力学与工程学报, 2004, 23(4): 561. LIU Baoguo, DU Xuedong. Visco-elastical analysis on interaction between supporting structure and surrounding rocks of circle tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(4): 561. [12] Fahimifar A, Tehrani F M, Hedayat A,etal. Analytical solution for the excavation of circular tunnels in a visco-elastic Burger’s material under hydrostatic stress field[J]. Tunnelling and Underground Space Technology, 2010, 25(4): 297. [13] Nomikos P, Rahmannejad R, Sofianos A. Supported axisymmetric tunnels within linear viscoelastic burgers rocks[J]. Rock Mechanics & Rock Engineering, 2011, 44(5): 553. [14] 王华宁, 曹志远, 李悦. 考虑断面及纵向施工效应时支护圆形洞室黏弹解析分析[J]. 岩土工程学报, 2011, 33(8): 1159. WANG Huaning, CAO Zhiyuan, LI Yue. Analytic researches on lined circular tunnels in viscoelastic rock mass considering effects of cross-section and longitudinal construction[J]. Chinese Joural of Geotechnical Engineering, 2011, 33(8): 1159. [15] Wang H N, Li Y, Ni Q. Analytical solutions for the construction of deeply buried circular tunnels with two liners in rheological rock[J]. Rock Mechanics & Rock Engineering, 2013, 46(6): 1481. [16] 焦春茂, 吕爱钟. 黏弹性圆形巷道支护结构上的荷载及其围岩应力的解析解[J]. 岩土力学, 2004(S1): 103. JIAO Chunmao, LU Aizhong. Analytical solution of loads on supporting structure for circular tunnel and stresses in viscoelastic surrounding rock[J]. Rock and Soil Mechanics, 2004(S1): 103. [17] 卞跃威, 夏才初, 肖维民, 等. 非静水压力场中考虑应力释放的圆形隧道黏弹性解[J]. 岩石力学与工程学报, 2013, 32(S2): 3455. BIAN Yuewei, XIA Caichu, XIAO Weimin,etal. Viscoelastic solution of circular tunnel under asymmetric hydrostatic pressure considering stress release[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(S2): 3455. [18] 苏锋, 陈福全, 施有志. 深埋双隧洞开挖的解析延拓法求解[J]. 岩石力学与工程学报, 2012, 31(2): 365. SU Feng, CHEN Fuquan, SHI Youzhi. Analytic continuation solution of deep twin-tunnels[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(2): 365. [19] 王华宁, 蒋明镜, 何平. 流变岩体中椭圆洞室断面开挖过程的力学分析[J]. 岩土工程学报, 2013, 35(11): 1979. WANG Huaning, JIANG Mingjing, HE Ping. Analytical solutions for elliptical tunnels in rheological rock considering excavation [J]. Chinese Journal of Geotechnical Engineering, 2013, 35(11): 1979. [20] 杨挺青. 黏弹性力学[M]. 武汉:华中理工大学出版社,1990. YANG Tingqing. Viscoelastic mechanics[M]. Wuhan: Huazhong University of Science Press, 1990. [21] 何平, 王华宁.深埋圆形压力隧洞施工过程的黏弹性解析解[J]. 力学季刊, 2012, 33(1): 45. HE Ping, WANG Huaning. Analytical viscoelastic solution of deeply buried circular tunnel considering excavation process[J]. Chinese Quarterly of Mechanics, 2012, 33(1): 45. [22] 张宁. 岩体初始地应力场发育规律研究[D]. 杭州: 浙江大学, 2002. ZHANG Ning. Study on the current crustal stress field in the rockmass[D]. Hangzhou: Zhejiang University,2002. [23] Feng X T, Chen B R, Yang C X,etal. Identification of visco-elastic models for rocks using genetic programming coupled with the modified particle swarm optimization algorithm[J]. International Journal of Rock Mechanics & Mining Sciences, 2006, 43(5): 789. Analytical Solutions for the Construction of Circular Tunnel Accounting for Time-dependent Characteristic of the Rheological Rock WANGHuaning1, 2, 3,SONGFei1,JIANGMingjing4 (1. School of Aerospace Engineering and Applied Mechanics, Tongji University, Shanghai 200092, China; 2. Key Lab of Highway Construction & Maintenance Technology in Loess Region, Ministry of Transport, PRC, Shanxi Transportation Research Institute, Taiyuan 030006, China; 3. Shanxi Key Laboratory of Highway Construction & Maintenance Technology in Loess Region, Shanxi Transportation Research Institute, Taiyuan 030006, China; 4. College of Civil Engineering, Tongji University, Shanghai 200092, China) The problems of lined circular tunnel construction subject to non-hydrostatic initial stresses were considered, accounting for cross-section excavation, longitudinal advancement, and any installation time of the elastic liner. In the derivation, linear viscoelastic models were adopted to simulate the rheological properties of the rock, time dependent excavation process and fictitious stresses were considered to simulate sequential excavation and tunnel advancement, respectively. According to the complex variable method and Laplace transform technique, the boundary and compatibility conditions were expressed by the two potentials, and the equations with respect to the coefficients in potentials were established afterwards. The analytical solutions for stress and displacement were then provided for the whole construction process after the determination of the coefficients by solving these equations. A good agreement between results from Finite Element Method and the analytical solutions had been obtained. Based on analytical solutions, a comprehensive parametrical analyses were then carried out to investigate the distribution discipline of displacements and stresses of the rock, as well as the influence of liner installation time on displacements and stresses of the rock. According to presented solutions, a fast predicting system for the mechanical state of the rock can be obtained and the ones provide much convenient way for preliminary design of tunnel construction. tunnel; support; viscoelastic; sequential construction; analytical solution 2016-02-22 国家自然科学基金(11572228,51639008);黄土地区公路建设与养护技术交通行业重点实验室开放基金(KLTLR-Y13-15);国家“九七三”重点基础研究发展计划 (2014CB046901) 王华宁(1975— ),女,教授,博士生导师,工学博士,主要研究方向为岩土工程数值与解析方法. E-mail: wanghn@tongji.edu.cn TU435 A












4 理论计算与有限元结果的对比

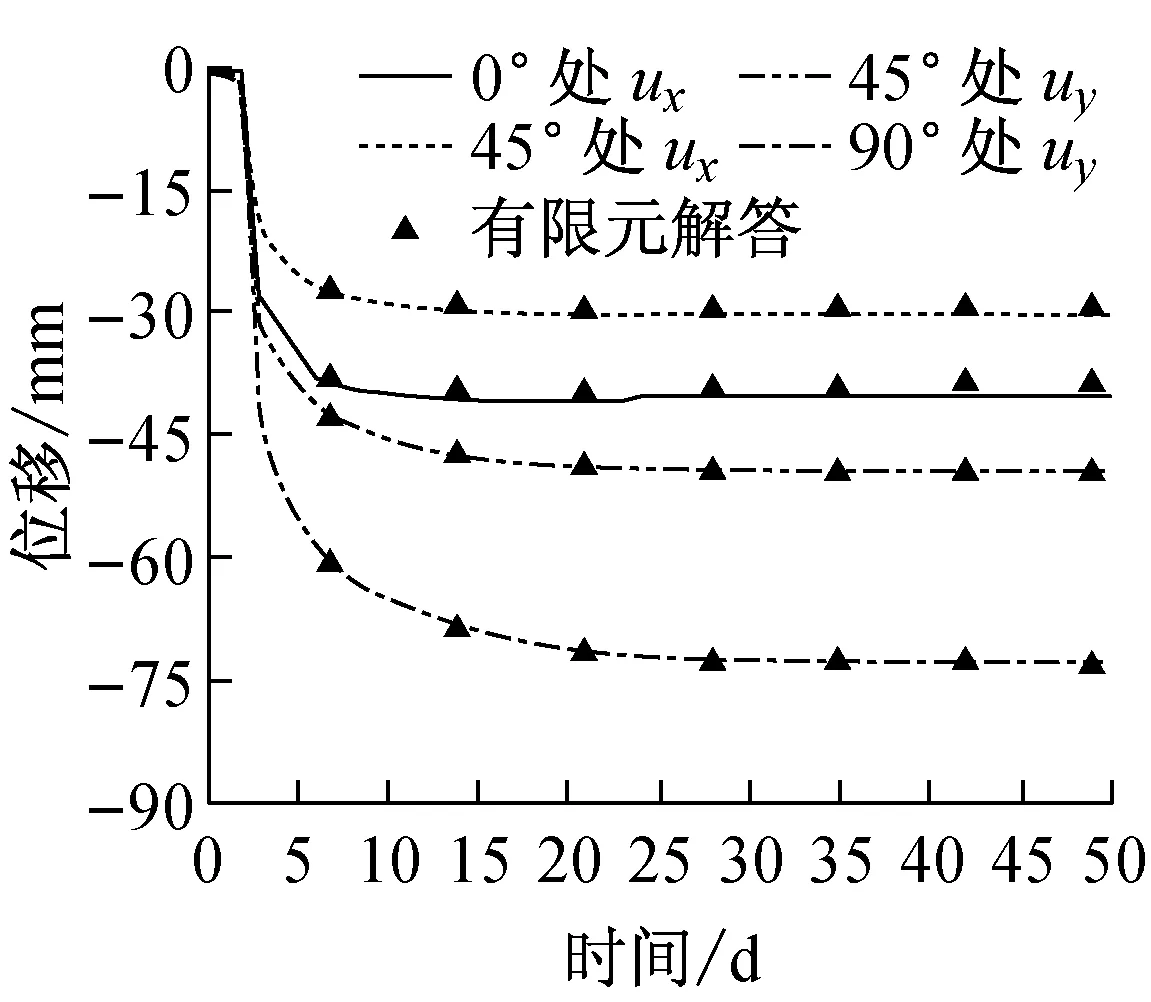

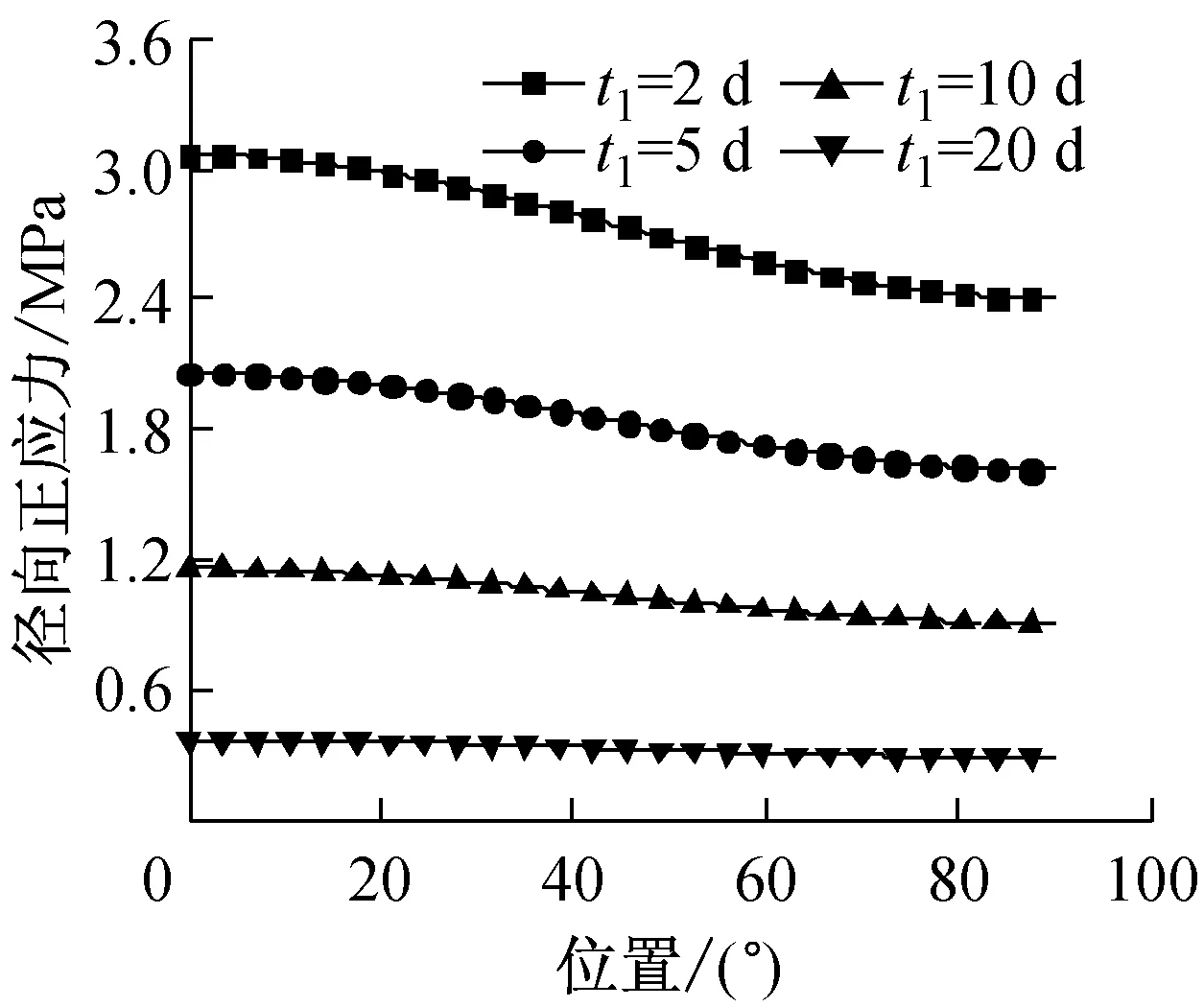
5 算例分析









6 结论
