关于储能设备优化定位的思考

徐 毅

（国网冀北电力有限公司经济技术研究院, 北京 100038 ）

关于储能设备优化定位的思考

徐 毅

（国网冀北电力有限公司经济技术研究院, 北京 100038 ）

随着风能在电力系统中占比的不断增长,其对电力系统运行控制的重大影响越来越被重视。电力储能设备能够在削峰填谷和加强系统可靠性方面提供很好的解决方案。因此,电力储能设备的选址问题就成为了一个需要研究的课题。针对这一问题提出了一种关于储能设备单元在有风能的电力系统中的优化定位方法,即通过遗传算法来确定储能设备的最佳位置。最后, 将该方法应用于有改进的IEEE 24 节点的系统中,并分析说明其结果,证实其有效可行。

电力储能；优化定位；最优潮流；概率最优潮流；风能

0 引言

电力系统运营者需要提供高效优质的服务来满足电力市场的需求。近些年，新兴能源一直保持增长态势，尤其是风能的增长尤为突出。2012年，风能是美国新增发电容量中最主要的来源，这甚至比其他新兴能源的总和还多[1]。与此同时，这些绿色清洁能源的不确定性和间歇性也对电网的可靠性带来影响。在新兴能源为高占比的电网运行中，当面对不可预测的突然的新型能源的产出的减少或者用电需求的增加时，电力储能设备的使用被认为是有效处理这种变化的方案。

大规模储能设备能够使用多种形式的能量然后再转化为电能，比如化学能、动能等[2]。主要的功能包括有减少运行成本、延后输电网的升级扩张、削减备用容量等。进而，电力储能设备的定位问题就成为了亟待解决的主要课题。在有风能的电力系统中，储能设备的优化定位可以带来巨大的效益并使其充分发挥所具有的功能。风能输出的巨大变化能够以恰当的方式通过储能设备调节。利用储能设备一般的工作方式是用其存储过剩的风能并在合适的时间进行放电。但是并不存在有统一固定的工作方式，根据具体的情况也存在有多种不同的灵活工作方式。优化电力储能设备定位目的是在满足系统各方面的约束条件下使得电力储能设备发挥最大作用。

与电力储能系统方面相关的研究已经开展多年了，最早是开始于1963年的水力火力协调方面的研究。随着科学技术的发展，更多不同形式的储能方式被开发并应用到系统中，比如，飞轮、压缩空气储能系统CAES（Compressed Air Energy Storage）、电池等。近几年，绝大多数的研究都集中在调度与协调与其他类型发电厂的配合上。根据具体的研究目的，多种建模方法被发展并应用。例如，德国的离散型电力市场模型被用于估计大规模风能发电厂在系统运行和CAES储能设备投资经济效益之间的影响关系[3]。只有极少数的研究关注于储能设备在有新兴能源的电网中的优化定位问题[4-6]。所有这些研究都是小储能设备在配电网中的应用。也有少数研究[7-9]是在输电网背景下进行的。但是，其中部分研究[8-9]是使用确定模型建模，这就欠缺了对新兴能源自然属性的考虑。在文献[7]中，所使用的多变量2m点估算方法的准确性问题还待商榷。再者，在对环境问题不断关注的背景下，这些研究中都没有将CO2价格这个重要因素考虑进去。

本文中使用概率化最优潮流方法和遗传算法来优化电力储能设备在含有风电厂的电力系统中的优化定位问题。优化定位储能设备主要包括2个步骤。概率化优化最优潮流的主要作用是通过2m+1点估算法最小化运行费用，遗传算法的主要作用是根据适应性函数筛选出最合适的配置点。最后，将上述方法应用于一个有改进的IEEE 24 节点的电力系统中，并对结果做出相应的说明。在本示例中储能设备工作的方式为之后的进一步研究提供了有价值的数据参考。

1 储能设备优化定位方法

1.1 一般流程

图1描述了确定电力储能设备最优化定位的一般化流程。其中风能和负荷作为输入量,即为概率化最优潮流计算的变量。遗传算法用于寻找储能设备的最适合定位点。必要时对上述步骤进行循环。

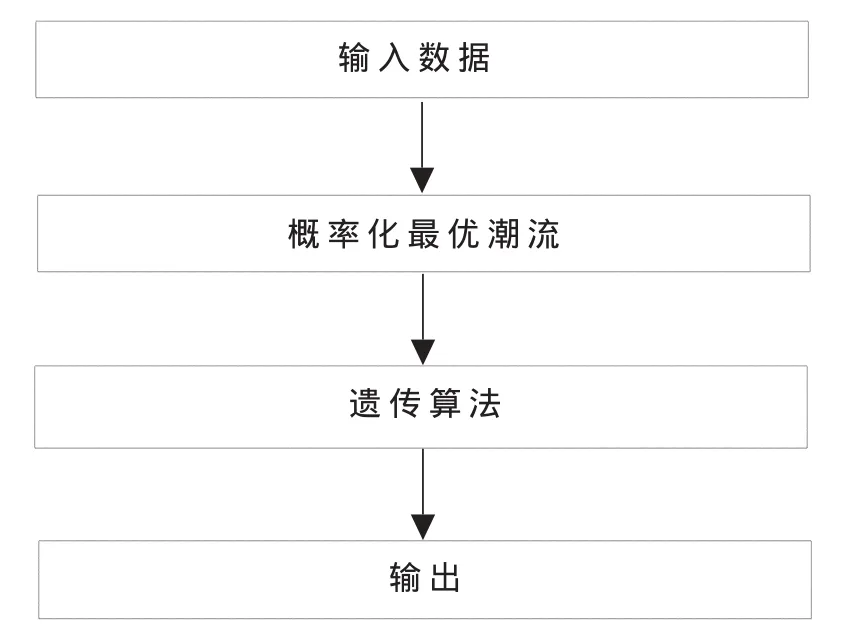
图1 优化定位一般化流程

1.2 概率化最优潮流

与传统方法相比，概率化最优潮流POPF （Probabilistic Optimal Power Flow）方法提供了更实际可行的结果因为充分考虑了风能的特性。目前存在有很多不同的建模方法来处理风能的不确定性，比如Monte Carlo 模拟法、分析法等。本文使用的点估计法是通过计算随机变量的矩来实现的。文献[10]研究中所使用的用于解决潮流问题的点估计法要优于文献[11]和文献[12]的方法。特别是2m+1 方法的准确性明显由于2m 方法，且运算效率也高于3m 方法。

图2是对点估算法的一般性描述。对于给定的输入数据，图中底部的实线通过若干选定的点来估算出输出数据的分布特性。

被选定的点的坐标为（pl,k, wl,k），它与其他变量间的关系表达式为

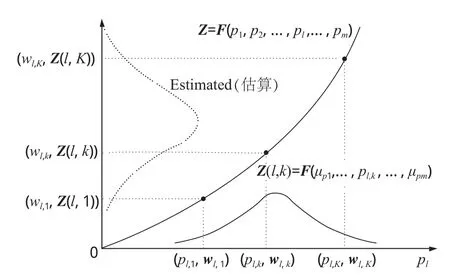
图2 点估算法的一般性描[10]

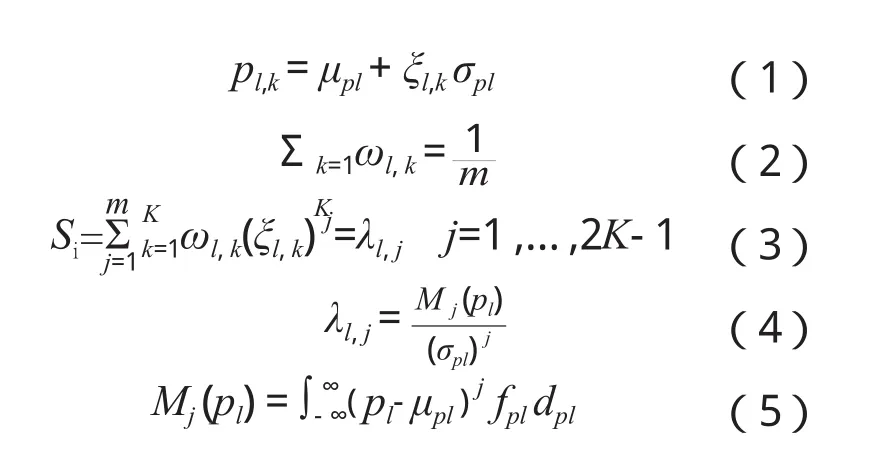
其中,（pl,k, ωl, k）是变量pl的第k个中心距。ξl, k是标准定位。μpl和σpl分别是输入数据的平均值和方差。λl, j是输入数据的第j个标准中心矩。变量m是指输入变量的个数。fpl是pl的概率密度函数。

对于2m+1方案，则有如下数据。其中，K=3 , ξl, 3=0， 则有

图3展示了2m+1方案的具体实现步骤。

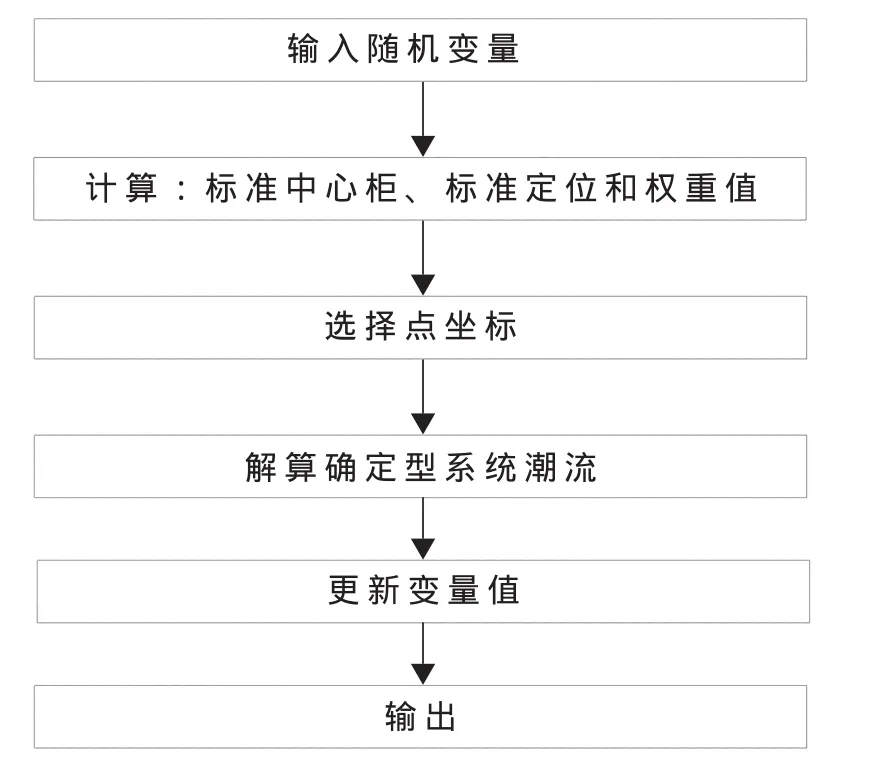
图3 2m+1方案流程

1.3 风能的模拟方案

风能是通过风速的历史数据转换而来。风速被模拟为1个2个参数的韦伯分布，其概率密度函数如式（9）所示，曲线拟合的方法用于估算其参数。风机的输出与风速的关系[13]如式（10）所示。当风速低于切入风速或高于切出风速时，其风能输出为零；当风速介于额定风速和切出风速中间时，风能输出为额定风力发电机功率；当风速介于切入风速和额定风速中间时，风能输出为一定比例的额定风力发电机功率。

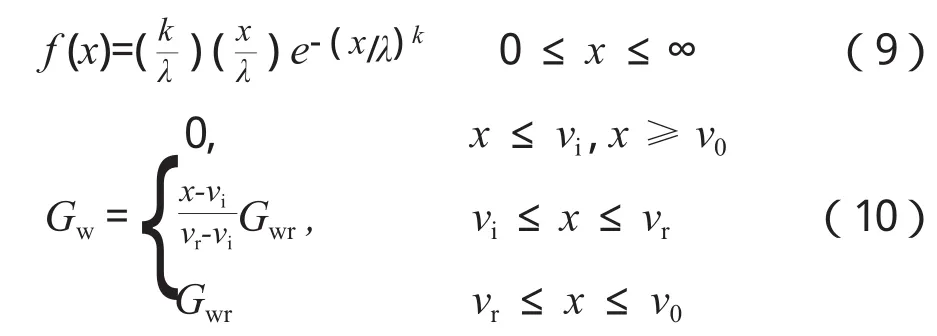
其中，f (x)是以k和λ为参数的韦伯分布函数，Gwr是风力发电机功率，Gw是风能输出，vi是切入风速，v0是切出风速，vr是额定风速。

1.4 最优潮流

输变电工程建设需要大量的建筑材料、物资、生产设备的购买费用和维修费用，还有施工人员的工资、奖金、社保等费用。

MATPOWER是一个由Zimmerman等开发的基于Matlab的开源电力系统仿真程序包[14]。使用MATPOWER解析确定型的电力系统模型，用其最小化目标函数，如式（11）所示。同时在最优潮流中考虑了CO2排放价格。其展开的具体形式如式（12）所示。

其中，Cj表示燃料价格，e fj是CO2的排放系数，Cco2是CO2的价格，Pi表示第i台发电机的有功输出，ki0，ki1和ki2为热耗率系数。

1.5 遗传算法

遗传算法的使用是为了找到最合适的储能设备定位点。需要达到的目标包含在适应性函数式（13）中。

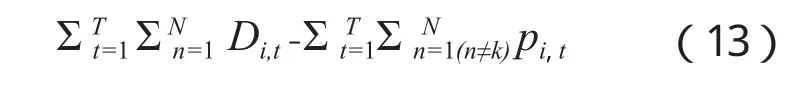
其中，D表示负荷侧的需求，P表示来自电源的有功，k表示储能单元所在的节点。适应性方程表示储能设备的充电量。遗传算法中，参数的设置很关键。一个合适的种群数量的选取能够改善结果的收敛性。

2 应用举例

本文的测试系统选用有改动的IEEE 24节点系统[15]，如图4所示。将风电场置于第19个节点，因为通常情况下风电站远离负荷中心。负荷的允许参数来源于德克萨斯电力可靠性委员会ERCOT的官方网站，是2013年3月1日的每小时负荷参数文档。

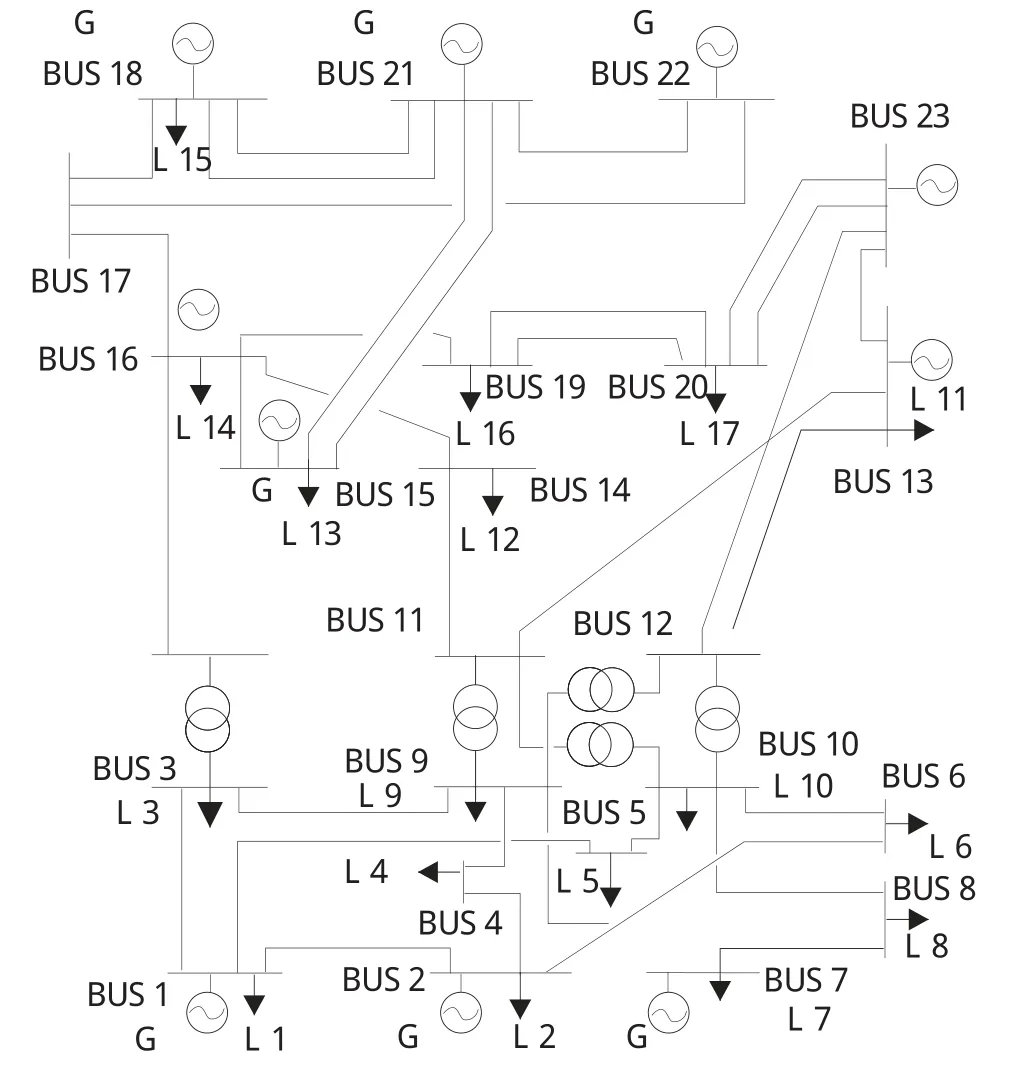
图4 IEEE 24 节点系统图

储能设备工作模式是指设备具体何时充放电。它根据不同的情况有多种模式，都对结果有直接影响。

本例中储能设备和风电场配合工作，吸收多余的风电。本例中风电场优先给邻近的负荷中心供电，再将富余的电能存储，如若风电场不能够满足周围的用电需求，则储能设备开始放电。

2.2 结果

在不同功率的风电场情况下，最优化的储能设备定位节点如表1所列。所示信息表明，随着风电场功率的升高，储能设备更倾向于靠近负荷中心。当风电场功率处于100 MW至200 MW时，储能设备处于高电压等级的节点上。如图5所示，储能设备的充电量和利用率随着风电场功率的升高而上升。其中，利用率是储能设备的充电量与额定风电发电量的比值。由储能设备的工作方式可知，这是对富余风电的有效利用。

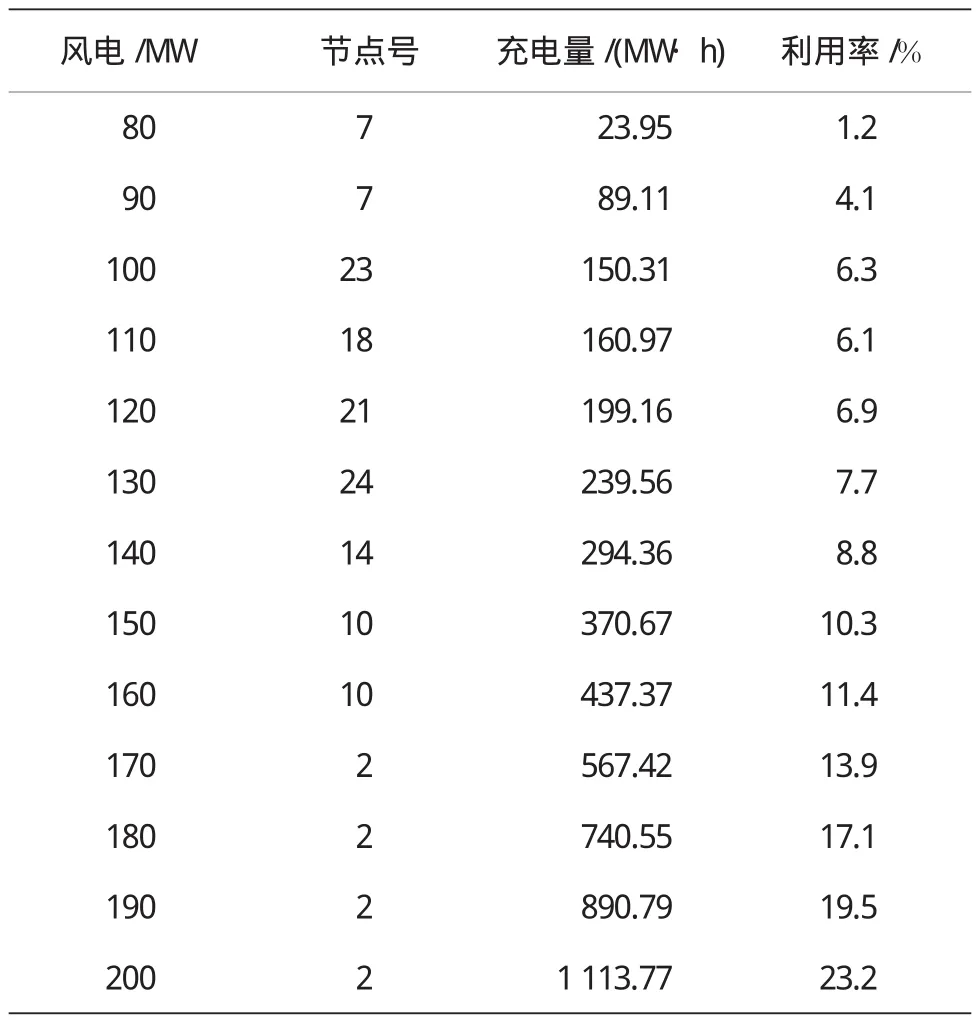
表1 示例结果信息表

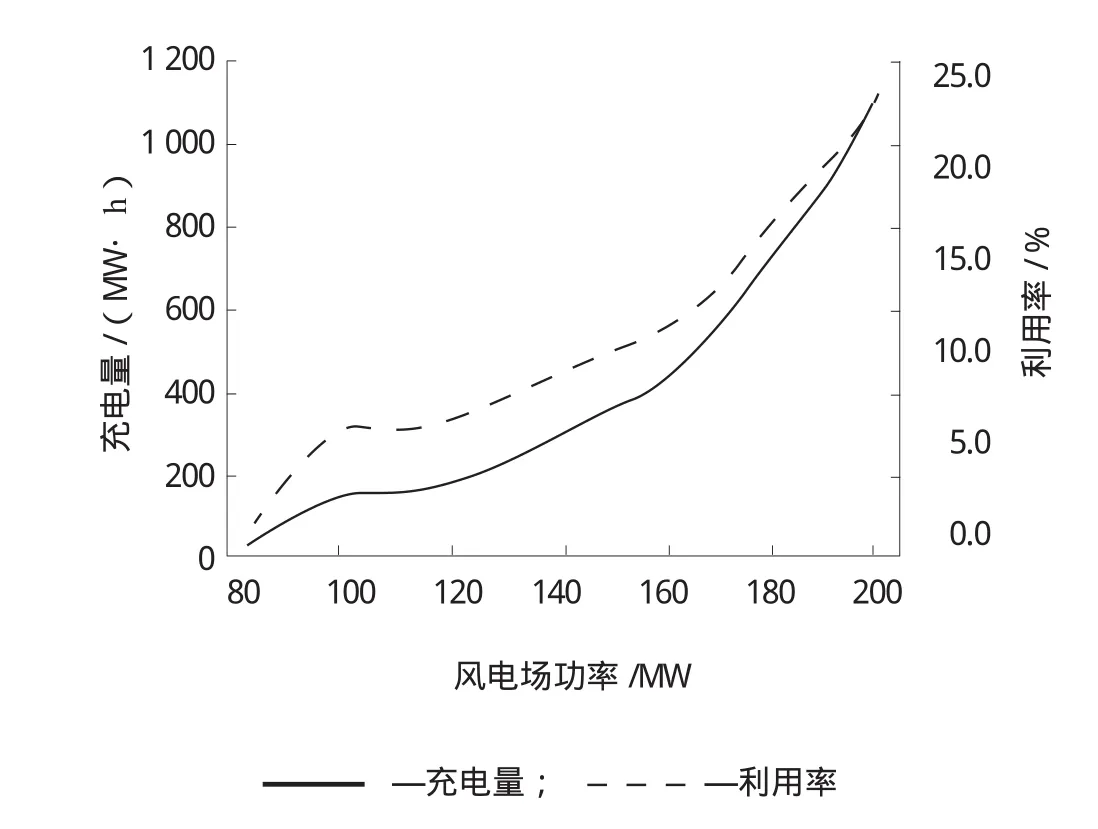
图5 充电量和利用率曲线图

图6所示为测试系统在有无储能设备时运行成本费用的比较。显而易见，有储能设备时的费用远低于无储能设备。在无储能设备的情况下，随着风电场输出功率的升高，费用降低，如图中实线所示。在有储能设备的情况下，随着风电场输出功率的升高，费用升高，如图中虚线所示在风电场输出功率约为160 MW时，费用上升明显加快，因为根据储能设备的工作模式，此时其较少有时机放电，需要传统发电机增大输出以满足负荷需求，使得费用快速增加。

图6 运行成本费用的比较图

图7所示为测试系统在有无储能设备时CO2排量的比较。其基本特征与图6相似，原因相同。

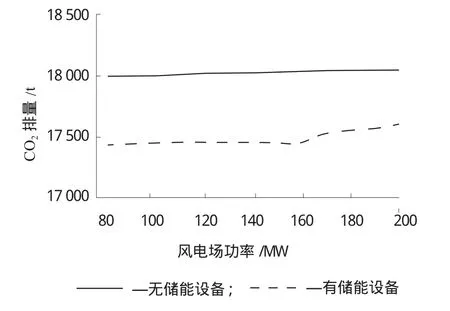
图7 CO2排放量比较图

3 结束语

本文给出了一种通用有效的方法用于在有新能源的电网中优化储能定位。该方法通过2m+1方案和遗传算法，降低运行成本费用和提高储能设备利用率，寻求储能设备最优定位点。以有修改IEEE 24节点系统为实例显示了有储能设备相配合运行的优点。其中储能设备的工作模式是关键因素。示例说明了该方法的准确性和高效性，同时其仍有更多改进之处有待进一步探讨。

[1] R. Wiser, M. Bolinger, 2012 wind technologies market report[R]. U.S. Department of Energy DOE/GO-102013-3948, 2012.

[2] V. Vittal, G. T. Heydt, S. Hariharan, et al. Tools and Techniques for Considering Transmission Corridor Options to Accommodate Large Scale Renewable Energy Resources[R]. PSERCProject S-41 Report, 2012.

[3] D. J. Swider. Compressed Air Energy Storage in an Electricity System With Significant Wind Power Generation[J].Energy Conversion, IEEE Transactions, 2007( 22): 95-102.

[4] G. Celli, S. Mocci, F. Pilo, et al. Optimal integration of energy storage in distribution networks[J]. Power Tech, 2009 IEEE Bucharest, 2009:1-7.

[5] G. Carpinelli, F. Mottola, D. Proto, et al.Optimal allocation of dispersed generators, capacitors and distributed energy storage systems in distribution networks[J].Modern Electric Power Systems (MEPS), 2010 Proceedings of the International Symposium, 2010:1-6.

[6] A. K. Basu, S. Chowdhury, and S. P. Chowdhury. Impact of Strategic Deployment of CHP-Based DERs on Microgrid Reliability[J]. Power Delivery, IEEE Transactions,2010(25):1697-1705.

[7] M. Ghofrani, A. Arabali, M. Etezadi-Amoli.A Framework for Optimal Placement of Energy Storage Units Within a Power System With High Wind Penetration[J]. Sustainable Energy, IEEE Transactions, 2013( 4)：434-442.

[8] S. Bose, D. F. Gayme, U. Topcu, et al. Optimal placement of energy storage in the grid[J]. Decision and Control (CDC), 2012 IEEE 51st Annual Conference, 2012: 5605-5612.

[9] K. Dvijotham, S. Backhaus, and M. Chertkov. Operations-based planning for placement and sizing of energy storage in a grid with a high penetration of renewables[J].arXiv preprint arXiv:1107.1382, 2011.

[10] J. M. Morales and J. Perez-Ruiz. Point Estimate Schemes to Solve the Probabilistic Power Flow[J].Power Systems, IEEE Transactions, 2007(22): 1594-1601.

[11] K. Li. Point-estimate method for calculating statistical moments[J]. Journal of Engineering Mechanics, 1992(118): 1506-1511.

[12] M. E. Harr. Probabilistic estimates for multivariate analyses[J]. Applied Mathematical Modelling, 1989(13): 313-318.

[13] S. Roy. Market constrained optimal planning for wind energy conversion systems over multiple installation sites [J]. Energy Conversion, IEEE Transactions,2002(17): 124-129.

[14] R. D. Zimmerman, S. Murillo, x, C. E. nchez, and R. J. Thomas. MATPOWER: Steady-State Operations, Planning, and Analysis Tools for Power Systems Research and Education[J].Power Systems, IEEE Transactions, 2011(26):12-19.

[15] C. Grigg, P. Wong, P. Albrecht, et al. The IEEE Reliability Test System-1996. A report prepared by the Reliability Test System Task Force of the Application of Probability Methods Subcommittee[J].Power Systems, IEEE Transactions, 1999(14):1010-1020.

Optimal Location of Energy Storage Equipment

XU Yi

（State Grid Jibei Electric Economic Research Institute, Beijing 100038, China）

With the gradually increased proportion of wind energy in power system, the significant impacts of wind energy on power system operation got more attentions. Electrical energy storage equipment provides a satisfied solution on peak shaving operation and reliability enhancement. The location problem for electrical energy storage is becoming a prominent issue needing to be figured out. This paper gives a general procedure on optimal location of storage unit in a power system with wind energy. Wind generation is modeled probabilistically using actual wind speed historical data. Then the genetic algorithm is used for selecting the desired location for a storage unit. The proposed method is applied on a modified IEEE 24-bus system, and it is verified to be feasible.

power energy storage; optimal location; optimal power flow; probabilistic optimal power flow; wind energy

TM910

A

1671-0320（2016）04-0011-05

2016-05-09，

2016-06-12

徐 毅（1983），男，山西太原人，2014年毕业于美国威奇塔州立大学电气工程专业，博士，工程师，主要研究方向为电力系统优化运行。