汽车燃油喷射系统用磁致伸缩驱动构件的建模与特性研究*

刘慧芳，赵俊杰，王文国，杨国哲，高子津

（1.沈阳工业大学机械工程学院，沈阳110870；2.华晨汽车工程研究院，沈阳110141）

汽车燃油喷射系统用磁致伸缩驱动构件的建模与特性研究*

刘慧芳1*，赵俊杰1，王文国2，杨国哲1，高子津1

（1.沈阳工业大学机械工程学院，沈阳110870；2.华晨汽车工程研究院，沈阳110141）

针对传统发动机喷射系统存在的非无级控制及喷射量难于精确最小化的问题，论文提出一种利用磁致伸缩致动器直接驱动喷嘴针控制燃油喷射过程的磁致伸缩喷射系统。通过调整磁致伸缩材料变形量以快速无级控制喷射器开合尺寸及喷射量。以基于多值函数算子现象学方法的磁滞理论为基础，结合对致动器系统的动力学特性分析，建立了包含磁滞损耗特性的位移模型。结果表明，模型可较准确描述磁致伸缩驱动构件的位移幅值及频率特性，位移预测平均相对误差约为5.6%；系统一阶谐振频率和位移峰值分别为380 Hz和50 μm。研究结果为改善喷射系统性能提供一种新方法。

磁致伸缩致动器；发动机喷射系统；模型；汽车

喷油器是汽车燃油系统的重要组成部分，不但向发动机缸体精确地提供雾化燃料，而且对降低燃油消耗至关重要。传统喷油器多数为电磁吸力工作方式，在每次吸气冲程中燃油仅喷射一次，流量控制通过调整喷油时间进行且为非无级控制，怠速工况下很难在短时间内实现喷射器的打开与关闭。为了优化喷射系统性能缩短调整喷油时间，需加快发动机燃料排放核心技术的发展，对其结构进行改进。

稀土超磁致伸缩材料GMM（Giant Magnetostrictive Materials）是一种新型功能材料，利用其在外部磁场作用产生变形的磁致伸缩效应特性开发的超磁致伸缩致动器GMA（Giant Magnetostrictive Actuator）可精密地输出微位移（最小位移可达0.001 μm～0.010 μm），实现电磁能向机械能转换［1-2］。该类致动器具有输出力大、频率响应平稳、温度范围宽、低压驱动、精度高等特点，已在精密加工、光学调整、声呐系统国防等高性能驱动领域表现出广阔的应用前景［3-6］。也可利用其受外界力作用导致内部磁化状态发生改变的磁致伸缩逆效应制作传感器，孙英、谢苗［7-8］等人基于磁致伸缩逆效应原理设计了磁致伸缩液位传感器。磁致伸缩喷射系统将GMA集成于喷油器中，利用GMA直接驱动喷嘴针阀实现对发动机燃油喷射过程控制［9］。通过调整GMM变形量快速控制喷射器开合尺寸及喷射量，能够实现对燃油流量的快速无级控制；利用该材料的高频响应特性结合小型化潜力，可以在每个燃烧周期中进行多次喷射；并且，还可实现引燃喷射、主喷射、后喷射、以及将主喷射划分为多次喷射的精确燃油喷射控制策略，保证发动机工作在最佳状态。与电磁燃油喷射系统相比，磁致伸缩喷射系统功率提高5%，噪声降低3 dB。

磁致伸缩喷射系统是一种能够改善汽车发动机控制性能、精度及响应速度的新一代燃油喷射器，在该系统中保证喷油量精确的关键是准确控制GMA位移，即建立描述位移与磁场及磁化强度间关系以及材料磁滞特性的数学模型。目前，描述GMM非线性磁滞行为的模型主要包括Maxwell模型、J-A磁化模型等。Maxwell模型适用于工作频率低于致动器系统一阶共振频率的情况［10］；J-A模型源于铁磁材料的磁畴理论，可清晰揭示材料的磁化过程机理，但模型参数辨识较为复杂困难［11-12］。Preisaach模型基于多值函数的算子，利用现象学方法描述了引起磁滞问题的所有因素，建模过程只考虑引起系统磁滞的所有输入因素和输出［13］，无需考虑磁致伸缩效应的发生机制，模型表达相对简单且控制器设计过程易于实现。因此，本文以Preisach磁滞理论为基础，为用于汽车发动机喷射系统中的超磁致伸缩驱动构件建模。论文阐述了磁致伸缩汽车发动机喷射系统的工作原理，设计了具有精密位移输出的GMA系统；基于Preisach磁滞理论和发动机燃油喷射系统实际工作过程，建立了描述GMA输出位移、磁致伸缩应变、磁场与磁化强度间关系的动态数学模型；并通过实验分析了GMA系统的频率响应等特性。研究成果将推动超磁致伸缩汽车发动机喷射系统的应用与推广，对改善发动机喷射系统的性能具有重要意义。

1 磁致伸缩燃油喷射系统的工作原理

1.1 喷射系统结构

磁致伸缩燃油喷射系统主要由GMA、液压连杆、伺服阀和喷嘴针组成，结构如图1所示。喷嘴针通过伺服阀控制，当GMA处于非工作状态，喷嘴针位于原始位置并且伺服阀关闭，高压区与低压区相互分离；通入工作后GMA开始工作，通过其输出位移的变化控制伺服阀开启，使控制室中压力减小，进而喷嘴被打开；如果伺服阀关闭，控制室压力增大，喷嘴针阀将关闭。在磁致伸缩燃油喷射系统中，推杆对喷嘴针无机械力作用，移动质量和摩擦均减小，因此燃油喷射的稳定性及误差得到显著改善。液压连接杆对热膨胀等因素引起的间隙进行补偿，并通过控制室旁的共轨压力保持喷嘴闭合。高压回路及低压回路中无泄漏位置，可提高整个系统的水力效率。磁致伸缩燃油喷射系统利用GMA直接驱动喷嘴针阀，取消了将喷嘴针运动传递到电磁喷油器控制室中的控制柱塞，液压传动线显著缩短，并且伺服阀和喷嘴针之间紧密连接，保证了喷嘴针对GMA运动做出快速反应。因此喷嘴针具有更高的速度，且易于实现稳定的最小喷油量。

图1 磁致伸缩燃油喷射器结构图

1.2 GMA结构设计与工作原理

GMA主要工作原理是利用磁致伸缩效应，受外界磁场作用时，GMM内部磁化状态变化并使其发生形变，材料变形通过传递机构以位移或力的形式传递给负载，进而实现负载驱动过程。本文采用模块化方法对GMA设计，主要由驱动模块和预紧模块组成，结构如图2所示。

图2 GMA结构

驱动模块完成GMM驱动及磁场监测功能，主要包括驱动线圈、磁路、磁场监测、传递机构及封装机构。通电线圈产生工作磁场，GMM棒轴向应变通过上导磁块和传递轴传递给外部负载。霍尔芯片通过直接测量与GMM内磁通密度成比例的磁通密度，实现对材料磁化状态的监测。根据磁通易通过低磁阻支路的原理，在霍尔芯片周围设计一阻磁圈以增加周围支路磁阻，进而提高磁场监测灵敏度。磁致伸缩效应与偏置磁场有关，本文利用在驱动线圈中叠加直流偏置电流的方式，为GMM同时提供驱动磁场和偏置磁场。该方法不仅易于偏置磁场调节，且克服了双线圈致使致动器质量大的弊端。GMM相对磁导率较低，所以利用上下导磁块、上下导磁盖及圆筒导磁轭等导磁单元增强GMM内部磁通并使其均布。预紧模块为GMM提供预紧力以改善磁致伸缩性能，其由预紧盖和碟形弹簧等构成。通过调节预紧螺栓与蝶形螺母间的螺纹旋合长度调整弹簧变形量，实现预紧力的调整。

2 超磁致伸缩构件的建模

根据GMA结构及工作过程，将建模过程分为四个阶段（如图3所示），即线圈通入电流后发生电磁效应而产生驱动磁场的模型，描述磁场作用下GMM磁化过程的模型，磁畴移动和转动使材料发生磁致伸缩效应而产生变形的磁致伸缩应变模型，磁致伸缩变形通过传递机构输出位移的运动模型。其中，磁化强度是联系磁场与磁致伸缩效应间的桥梁，决定了磁致伸缩应变、磁通密度及磁场强度之间关系，所以建立描述磁化过程的磁化模型尤为关键。致动器位移精度等工作特性受GMM自身存在的磁滞特性影响［14］，研究表明材料磁滞特性引起的位移误差最高可达20%，因此将材料磁滞特性考虑在执行器的建模过程中对于减小磁滞误差、提高执行器工作精度尤为重要。Preisaach磁滞理论以多值函数的算子为基础，利用现象学方法描述引起磁滞问题的所有因素，建模过程无需考虑磁致伸缩效应的发生机制，模型表达相对简单且控制器设计过程易于实现。因此，本节以Preisach磁滞理论为基础，结合GMA实际工作过程，建立描述位移、磁致伸缩应变、磁场及磁化强度间关系的动态数学模型。

图3 GMA建模流程框图

2.1 驱动磁场及磁化过程模型

GMM棒中磁场沿径向分布不均匀［15］，根据麦克斯韦方程，建立GMM棒中磁场分布的柱坐标系方程［16］：

其中，r为径向坐标，H为磁场强度；k2=jωμrσe，ω为磁场角频率，μr为GMM磁导率；σe为电导率，表达式为：σe=1/ρ，ρ为材料电阻率。

上式为GMM径向磁场的零阶修改贝塞尔方程表示，其解为一类修改贝塞尔函数I0(kr)。如果线圈产生的磁场强度为，半径为R的GMM棒内在r处的磁场分布为：

GMM电导率σe较大，因此当驱动频率ω也较大时，|kr|→∞。根据贝塞尔函数渐近公式［17］：

将上式代入（2）式中，得：

分析（4）式知，GMM棒中磁场强度在径向为非均匀分布，与径向坐标r有关，且磁场强度大小随工作频率变化。GMM棒径向横截面平均磁场强度表示为：

其中Sr为GMM棒横截面积。

经典Preisach理论认为铁磁材料由诸多磁偶极子组成，各磁偶极子具有一定的滞回特性，GMM材料的宏观滞回特性是各磁偶极子磁滞特性总和的表现。通过将各个磁偶极子磁化磁滞特性叠加计算GMM的总磁化强度，Preisach磁滞模型的输入与输出间的关系如图4所示。

图4 Preisach模型示意图

其中，γαiβi为第i个单位磁滞算子；μ(αi,βi)为第i个单位磁滞算子的权重函数，表示γαiβi所占的比例；α和β分别为系统输入的上升与下降阈值；vi为第i个单位磁滞算子的输出；u(t)和f(t)分别表示模型总输入与输出。

单位磁滞算子特性如图5所示，u为算子输入，v是算子输出。输入与输出关系为：

其中，θ∈{-1,1}。当输入u(t)＞α时，输出v(t)=1；当u(t)＜β时，v(t)=-1；当输入β＜u(t)＜α时，若输入单调增加到u(t)，输出v(t)=-1，若输入单调减小到u(t)，v(t)=1。

图5 单位磁滞算子示意图

模型总输出f(t)为：

在利用Preisach理论建立GMM磁化模型时，模型输出f(t)为材料内部平均磁化强度M，模型输入u(t)为平均磁场强度。权函数μ(α,β)数值分布在α-β平面内的三角形S区域内，即分布在Preisach平面上（如图6所示），该平面表示为：

图6 Preisach模型的积分区域

在实际应用中，α和β数值具有边界，即β≥β0，α≤α0，并且α≥β。在Preisach平面上S以外的区域中，密度函数μ(α,β)=0。在任意时刻，将S区域分为两个子区域，即S=S-(t)⋃S+(t)。

式（7）表示为：

式（11）中包含有双重积分，并且确定权函数μ(α,β)时需要对实验数据求二阶偏导数，模型计算过程较复杂且误差较大。因此，本文首先对上述表达式进行离散化处理，再利用数值分析方法完成模型的求解计算。根据输入终值处于上升阶段或下降阶段，将模型数值求解分为两种情况：当工作磁场u(t)从0单调增大到αk时，输出的磁化强度定义为f(αk)；磁场再单调下降至βk时，磁化强度定义为f(αk,βk)。模型的输出变化用F(αk,βk)表示，则：

当工作磁场单调增加时，磁化强度的离散化结果为：

当工作磁场单调减小时，离散结果为：

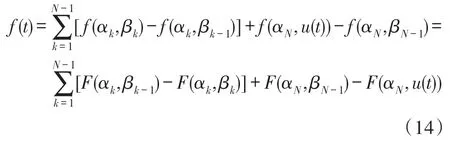
其中，N为工作磁场序列，αk和βk分别为磁场序列上升过程的极大值和下降过程的极小值。所以，根据工作磁场的单调变化特性，在磁场作用下发生磁化的GMM内部平均磁化强度可通过式（13）～式（14）确定。

2.2 磁致伸缩应变与输出位移模型

铁磁性材料在磁场作用下的磁致伸缩应变与驱动电流呈非单值函数关系，如果以电流强度或磁场强度作为控制量，则会影响材料的磁滞及非线性控制特性。因此，从磁致伸缩现象发生机制出发，选用与磁介质的磁化状态直接关联的磁化强度M作为控制量，建立磁致伸缩效应模型。利用基于能量的二次畴转模型描述在一定应力作用下磁致伸缩应变与磁化强度间的关系为［18］：

其中，λ为GMM的磁致伸缩应变，即磁致伸缩系数；Ms和λs分别为GMM的饱和磁化强度与饱和磁致伸缩系数，其数值通过材料的参数辨识确定。磁致伸缩伸长量为：

其中，ΔL和L分别为GMM棒伸长量与初始长度。将式（15）代入式（16）中，得伸长量与磁化强度间的关系为：

GMA系统以磁场为激励源、通过GMM棒伸长或缩短引起整个系统发生受迫振动，因此需结合动力学方法分析整个致动器系统输出特性。将GMM棒简化为由质量、弹簧和阻尼组成的单自由度系统，其伸长量为x（x=ΔL），致动器输出位移为y，利用达朗贝尔原理为整个致动器系统建立微分方程模型：

其中，Kt为GMM棒刚度、Km为位移传递机构刚度，mt为运动部件总质量，Ct为阻尼系数。对上式进行拉氏变换，得致动器系统传递函数：

分析系统传递函数可知，GMA为二阶系统。其中，K、ωn和ξ分别为系统增益、无阻尼固有频率和阻尼比，其与系统刚度、质量和阻尼系数关系分别为：

根据系统传递函数并进行拉氏反变换运算，得致动器输出位移响应y(t)为：

其中，ωd为系统有阻尼自然振荡频率，ωd=ωn×当时间t→∞时，求得系统输出位移稳态响应为：

GMM棒刚度Km和位移传递机构刚度Kt均为系统参数，因此对于确定的GMA系统，其输出位移与GMM伸长量成正比。

3 实验及讨论

为了验证超磁致伸缩驱动构件模型有效性，研制了用于汽车发动机喷射系统中的GMA样机，并进行了实验研究，实验系统如图7所示。GMA中的磁致伸缩元件是长度为50 mm、直径为8 mm的圆柱棒状TbDyFe，线圈匝数为200；双极性可编程电源为致动器提供工作电流，输出位移由激光位移传感器测量并且通过示波器监测显示。

图7 实验系统

为GMA提供幅值和频率分别为1 A和200 Hz的正弦电流，输出位移测量曲线和模型预测结果如图8（a）所示。结果表明，输出位移是与输入电流频率相同的简谐规律响应，位移峰峰值约为20 μm。为了验证模型稳定性，对致动器系统进行了位移跟踪实验。在逐渐衰弱的正弦振荡电流作用下，致动器输出位移如图8（b）所示。结果表明，GMA输出位移以电流频率按照正弦规律振荡，且幅值逐渐衰减。位移计算值与测量值间具有较好的吻合性，位移预测的平均相对误差约为5.6%。在波峰与波谷处，因电流方向突然变化导致GMM中磁畴不能快速旋转，因此位移具有较大偏差。上述建立的模型可较准确描述用于发动机喷射器系统中的GMA构件的位移幅值和频率等输出特性，且具有较好的稳定跟踪特性，可用于控制燃料喷射系统中GMA构件的工作过程。

图8 GMA输出位移的实验结果

另外，为研究GMA系统的谐振特性，并确定输出位移达到最大时的谐振频率，对致动器系统进行了频率扫描实验，频率特性测试是通过稳定频率步长正弦扫描激励方法进行。在实验频率范围内，致动器被逐一施加幅值恒定、频率以固定步长从低频到高频变化的激励电流，并且各频率状态下的激励电流信号与位移响应信号由示波器采集存储。扫频实验过程中，双极可编程电源通过电流恒定和频率转换模式为致动器提供激励电流模拟扫频激励。工作电流是幅值为0.5 A的正弦电流，扫频范围为0～2 000 Hz。频率在0～500 Hz范围时，频率变化步长为50 Hz；在500 Hz～2 000 Hz范围内，频率变化步长为20 Hz。扫频实验过程在0.55 s内完成，实验结果如图9所示。从结果曲线可以看出，所研制的用于燃料喷射系统中的GMA构件的一阶谐振频率约为380 Hz、谐振状态下的输出位移幅值约为50 μm。

图9 扫频试验结果

通过缓慢调整碟形弹簧变形量逐渐调节预紧力，同时测量致动器的位移幅值，得预紧力对位移影响的结果如图10所示。随着预紧力增大，位移先逐渐增大再减小；当预紧力约为18 MPa时，位移近似达到峰值状态。这是因为，在预紧力作用下GMM内磁畴先朝着垂直于磁场方向偏转，电流激励后，转向于磁场方向的磁畴数目与无预紧力相比增多、转动角度增大，进而使GMM变形量增大；但是，当预紧力过大时，磁场激励作用不能完全抵抗预紧力对磁畴运动的影响，此时预紧力将削弱GMM形变能力。因此，GMA存在一个最佳的预紧状态。

图10 位移与预紧力的关系

4 结论

以GMM的磁致伸缩效应特性为基础，提出利用GMA直接驱动喷嘴针实现燃油无级喷射的精密磁致伸缩发动机喷射系统，与传统电磁喷射器相比，液压传动线缩短且喷嘴针速度快、稳定性更高，且可得到更精确的最小燃油喷射量。完成了GMA结构设计，其由GMM棒、驱动模块、预紧模块和输出轴等组成。通过将GMA工作过程分解为线圈发生电磁效应产生驱动磁场、GMM发生磁化、磁化后磁畴运动导致磁致伸缩效应而产生变形、磁致伸缩变形通过传递机构输出位移4个阶段，以基于现象学方法的Preisach磁滞理论为基础，结合对致动器系统的机械动力学特性分析，建立了包含磁滞损耗特性的GMA位移模型。实验结果表明，模型可较准确描述用于喷射器系统中的GMA构件的位移幅值及频率等输出特性，且具有较好的稳定跟踪特性，位移预测的平均相对误差约为5.6%；致动器系统的一阶谐振频率约为380 Hz、谐振位移幅值约为50 μm。研究结果将推动磁致伸缩发动机喷射系统的应用与推广，对改善发动机喷射系统的性能具有重要意义。课题组将进一步针对模型在波峰波谷处存在的预测偏差问题展开研究。

［1］Jin Ke，Kou Yong，Zheng Xiaojing.The Resonance Frequency Shift Characteristic of Terfenol-D Rods for Magnetostrictive Actuators［J］.Smart Materials and Structures，2012，21（4）：045020.

［2］王丽梅，董桉吉.超磁致伸缩致动器的基于RBF神经网络整定PID控制［J］.组合机床与自动化加工技术，2013，（5）：76-79.

［3］Tong D，Veldhuis S C，Elbestawi M A.Control of a Dual Stage Magnetostrictive Actuator and Linear Motor Feed Drive System［J］.International Journal of Advanced Manufacturing Technology，2007，33（3/4）：379-388.

［4］张雷，邬义杰，王彬，等.超磁致伸缩构建精密加工异形孔滑膜控制［J］.浙江大学学报（工学版），2012，46（8）：1412-1418.

［5］Liu Huifang，Wang Shijie，Ma Chao，et al.Study on an Actuator with Giant Magnetostrictive Materials for Driving Galvanometer in Selective Laser Sintering Precisely［J］.International Journal of Mechatronics and Manufacturing Systems，2015，8（3/4）：116-133.

［6］徐彭有，杨斌堂，孟光，等.天文望远镜子镜超磁致伸缩驱动器驱动模型及参数识别［J］.天文研究与技术，2010，7（2）：150-157.

［7］孙英，靳辉，郑奕，等.磁致伸缩液位传感器检测信号影响因素分析及实验研究［J］.传感技术学报2015，28（11）：1608-1613.

［8］谢苗，刘治翔，毛君.基于改进型ANFIS的磁致伸缩液位传感器温度补偿［J］.传感技术学报，2015，28（1）：50-55.

［9］Chowdhury H A，Mazlan S A，Olabi A G.A Simulation Study of Magnetostrictive Material Terfenol-D in Automotive CNG Fuel InjectionActuation［J］.SolidStatePhenomenaSeries，2009，154：41-46.

［10］孙华刚，袁惠群.超磁致伸缩材料内部磁场与涡流损耗理论分析［J］.东北大学学报（自然科学版），2008，29（3）：371-374.

［11］Li Yusong，Zhu Yuchuan，Wu Hongtao，et al.Modeling and Inverse Compensation for Giant Magnetostrictive Transducer Applied in Smart Material Electrohydrostatic Actuator［J］.Journal of Intelligent Material Systems and Structures，2014，25（3）：378-388.

［12］刘慧芳，贾振元，王福吉，等.超磁致伸缩执行器位移模型的参数辨识［J］.机械工程学报，2011，47（15）：115-120.

［13］Talebian S，Hojjat Y，Ghodsi M.A Combined Preisach-Hyperbolic Tangent Model for Magnetic Hysteresis of Terfenol-D［J］.Journal of Magnetism and Magnetic Materials，2015，396：38-47.

［14］王彬，屈稳太，邬义杰，等.超磁致伸缩材料磁滞建模方法国内外研究现状评述［J］.功能材料，2013，44（16）：2295-2300.

［15］崔旭，何忠波，李东伟，等.超磁致伸缩致动器能量损耗特性分析［J］.中国机械工程，2013，24（22）：2987-2991.贾振元，郭东明.超磁致伸缩材料微位移执行器原理与应用［M］.北京：科学出版社，2008.

［16］汪建新，高耀东，任冲珝.磁致伸缩材料在高频驱动时内部磁场分布及其对磁致伸缩性能的影响［J］.机械传动，2007，31（6）：21-23.

［17］Dapino M J，Smith R C，Flatau A B.Structural-Magnetic Strain Model for Magnetostrictive Transducers［J］.IEEE Transactions on Magnetics，2000，36（3）：545-556.

刘慧芳（1983-），女，辽宁朝阳人，沈阳工业大学机械工程学院讲师、硕士研究生导师、机械工程流动站博士后研究人员，主要研究方向为磁致伸缩精密微位移驱动与控制技术，hfliu@sut.，edu.cn；

赵俊杰（1992-），男，山东烟台人，沈阳工业大学机械工程学院硕士研究生，主要研究方向为磁致伸缩精密微位移驱动与控制技术，550726458@qq.com。

Study on Model and Characteristics Analysis of the Magnetostrictive Drive Component of Automotive Fuel Injection System*

LIU Huifang1*，ZHAO Junjie1，WANG Wenguo2，GAO Zijin1
（1.School of Mechanical Engineering，Shenyang University of Technology，Shenyang110870，China；2.Brilliance Auto Engineering Research Institute，Shenyang110141，China）

Aiming at the problem that non stepless control and spray quantity being difficult to be accurately minimized which exist in traditional engine injection system，a new magnetostrictive injection system was presented in this paper.It used a giant magnetostrictive actuator to drive nozzle needle directly in order to control the fuel injection process.Opening size and injection quantity of injector were controlled smoothly and rapidly by adjusting the deformation of magnetostrictive materials.On the basis of a hysteresis theory which is based on phenomenological method of multi valued function operator，and combining with the dynamic characteristics analysis of actuator system，a displacement model containing hysteresis loss characteristics was established.Results show that the model can describe the amplitude and frequency of displacement for giant magnetostrictive actuator well.Average relative error of displacement prediction is about 5.6%.The first order resonant frequency and peak value of displacement are about 380 Hz and 50 μm respectively.Research results will provide a new method for improving the performance of injection system.

magnetostrictive actuator；engine injection system；model；automobile

TP215；TP13

A

1004-1699（2016）12-1797-07

��3120J；3120G

10.3969/j.issn.1004-1699.2016.12.003

项目来源：国家自然科学基金项目（51305277）；教育部博士点科研基金项目（20132102120007）；中国博士后科学基金特别项目（2014T70261）；沈阳市科技计划项目（F15-199-1-14）

2016-05-31修改日期：2016-06-30