谐振式光纤陀螺偏振波动噪声的温度特性*

张 婷，郑 华，杜建功，安盼龙，闫树斌，薛晨阳

（中北大学电子测试技术重点实验室，太原030051）

谐振式光纤陀螺偏振波动噪声的温度特性*

张 婷，郑 华，杜建功，安盼龙，闫树斌，薛晨阳*

（中北大学电子测试技术重点实验室，太原030051）

光纤环形谐振腔环境温度变化带来的偏振波动噪声是影响谐振式光纤陀螺检测精度的主要光学噪声源之一，通过控制谐振腔温度，可以使偏振波动噪声得到有效抑制。为了抑制偏振波动噪声，减小R-FOG精度受FRR温度变化的影响，从理论上分析了谐振腔温度变化对谐振曲线、解调曲线的影响；针对不同温度下光纤环的谐振特性、解调曲线特性、陀螺零偏及零偏稳定性开展了实验，并对实验结果进行了分析。结果表明，谐振腔的工作温度为27.00℃时，两本征偏振态相距最远，总谐振曲线关于谐振频率点对称，谐振频率点检测误差可以忽略；陀螺零偏稳定性近似等于谐振腔温度为25.50℃时的1/100，在150 s的采样时间内达到0.07°/s，陀螺检测精度得到很大提高。

谐振式光纤陀螺；偏振波动噪声；温度控制；零偏稳定性；光纤环

谐振式光纤陀螺R-FOG（Resonator Fiber Optic Gyroscope）凭借其易于小型化、集成化，理论精度高等独特优势，在光学陀螺领域引起了研究人员的广泛关注。与干涉式光纤陀螺I-FOG（Interferometer Fiber Optic Gyroscope）相比，R-FOG实现相同的检测精度需要的光纤长度更短，同时减少了由于光纤环温度分布不均匀引起的漂移现象［1-2］。然而，由于各种光学噪声的存在，R-FOG精度受到了严重限制。目前，光Kerr效应还没有成为制约R-FOG精度提高的主要因素；通过双频率调制和载波抑制的方法可以很好地消除背散射噪声；但是，光纤环形谐振腔FRR（Fiber Ring Resonator）外界环境如温度等因素的随机变化所引起的偏振波动噪声，使陀螺输出产生了零偏和零偏不稳定的现象［3-4］，这在很大程度上降低了系统检测精度。

针对这个问题，1989年，Sanders G A等提出了偏振轴单次90°旋转熔接的偏振波动噪声抑制结构［5］。通过将两本征偏振态ESOP（Eigenstate Of Polarization）传输一周后的相位差控制到π［6］，且使该相位差不随FRR温度的变化而变化，可以在一定程度上抑制R-FOG中的偏振波动噪声。此时次偏振态S-ESOP（Secondary ESOP）与主偏振态P-ESOP（Primary ESOP）的相对距离最远，P-ESOP受到的干扰最弱。由于P-ESOP和S-ESOP能量处于基本均分状态，因此FRR输出光功率减小为输入光功率的一半；2009年，Hotate K等［7］利用偏振轴双次90°旋转熔接的方法，通过将两熔接点间的光纤长度差控制到保偏光纤拍长的一半，使得二者传输一周的相位差为π，得到两个线性ESOPS，在入射光波满足一定条件时可以选择性的激励出单一偏振态。这种方法可以有效地抑制偏振波动噪声，但是FRR中两熔接点的位置难以精确控制；Huilian Ma等又在此基础上提出了偏振轴双次90°旋转熔接的谐振腔内集成在线起偏器的偏振抑制模型［8］。这种结构增加了S-ESOP绕腔损耗，降低了偏振波动噪声，但同时降低了谐振腔精细度（F），谐振特性恶化。

为了抑制偏振波动噪声，减小R-FOG精度受FRR温度变化的影响，文中从理论上分析了谐振曲线及其解调输出的温度响应特性以及偏振波动噪声对R-FOG零偏和零偏稳定性的影响；通过对保偏FRR进行主动温度控制，测试了不同FRR温度下的谐振输出、解调输出和陀螺系统输出。选取合适的FRR工作温度可以有效提高R-FOG的零偏稳定性，对陀螺性能的优化具有重要意义。

1 偏振波动噪声产生原理与仿真

保偏光纤具有内在确定的高双折射率，远远大于由外部微小扰动引起的双折射效应，因此较单模光纤而言，其内部传输的光波偏振态稳定性提高，在RFOG偏振波动噪声抑制方面优势显著。然而，保偏光纤对外界环境如温度等因素的干扰仍然十分敏感。

随着保偏FRR温度的波动，光纤双折射发生变化，谐振腔内两ESOPS的传输常数随之改变，光波在谐振腔内传输一周后两ESOPS之间形成不固定的相位差Δφ，即二者的相对位置发生波动，该过程表示为［9］：

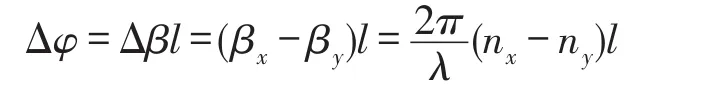
式中，λ为真空中光波长，nx、ny为光纤偏振轴对应的有效折射率，l为谐振腔腔长，βx和βy为两ESOPS的传播常数，Δβ为光纤双折射。

下面以保偏反射式谐振腔为例，说明FRR温度变化引起的偏振波动噪声对R-FOG整体性能产生的影响。该结构与保偏透射式谐振腔相比，耦合器的个数由两个减少为一个，光路传输损耗减小、结构简化、精细度更高。谐振腔结构如图1所示。

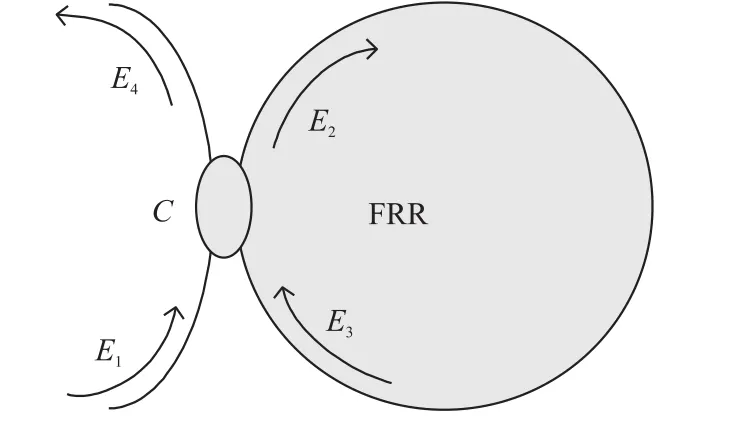
图1 反射式谐振腔结构示意图

图1中，耦合器C为保偏定向式耦合器；环腔内部光纤类型为PM15-U25D的熊猫型保偏光纤，当外界温度一定时保偏光纤拍长LB约为3 mm～5 mm，当FRR温度变化时，LB=λ/|βx-βy|会随之改变。Εj（j=1，2，3，4）表示谐振腔耦合器各端口的输入输出光波场，以顺时针（CW）传输光波为例：由耦合器1端口入射的光波，一部分直接透射到输出端口4；另一部分交叉耦合进2端口在FRR内绕腔传输，每经过耦合器一次，就有部分光由4端口输出，与直接输出光波发生干涉叠加。

采用琼斯矩阵描述各光学器件以及偏振态交叉耦合现象。光波由耦合器1端口到2端口、1端口到4端口的传输矩阵分别为［10］：

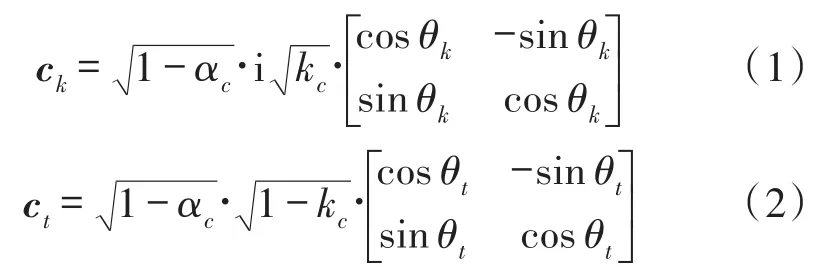
式中，αc、kc分别为耦合器C的插入损耗和耦合系数，θk、θt分别表示耦合器交叉端和直通端的等效偏振对准角度误差，耦合器偏振消光比εx(dB)= -10lg(tan2θx)（x=t,k）。εx越大，θx越小，耦合器偏振串音就越小。光波由耦合器2端口到3端口的传输矩阵为：

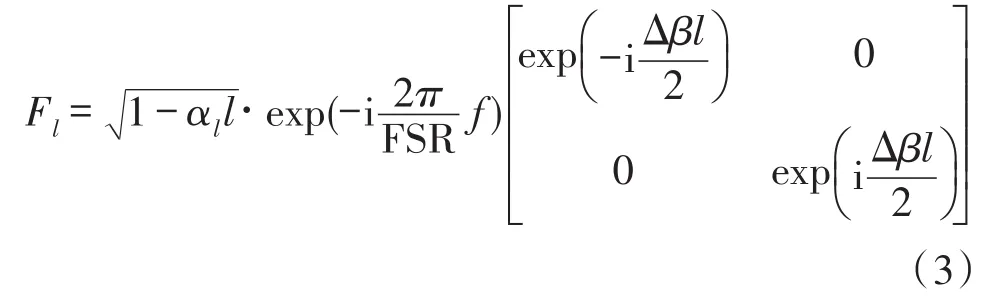
式中，αl为腔内传输损耗，FSR为谐振腔自由谱宽，FSR=c/(nl)，c为真空中光速，n为光纤纤芯有效折射率。光波在FRR内顺时针传输一周的矩阵为：

由等式

可以求得传输矩阵scw的特征值λcw和特征向量vcw。其中，λcw表示光波在谐振腔内传输一周后的幅度损耗和相位延迟，vcw表示谐振腔内传输的两个本征偏振态ESOPS。假设耦合器1端

口的入射光波场为：

其在两特征偏振轴v1cw和v2cw上的投影分量分别为a和b，则入腔光波可以表示为：

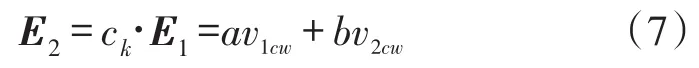
光波在谐振腔内传输多圈回到耦合器2端口后，两ESOPS光波场矢量为：

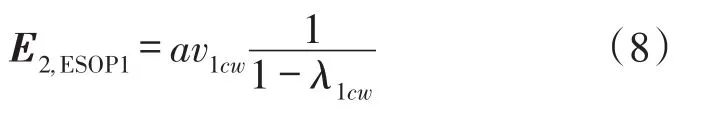
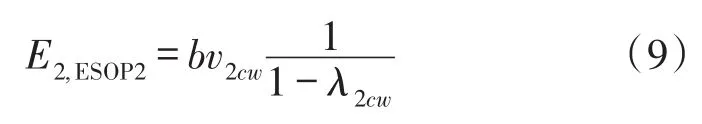
假设耦合器C偏振特性不相关、腔内离散点的偏振对准误差可以忽略，此时两ESOPS保持正交关系，二者在耦合器4端口发生干涉叠加，引起谐振曲线不对称，从而导致谐振频率点检测产生误差。耦合器2端口到4端口的输出光波场为：

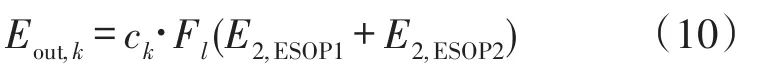
1端口到4端口的输出光波场为

耦合器C总输出光波场为：

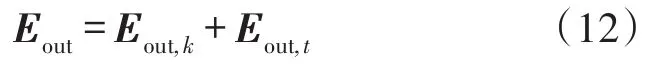
总输出光强表示为：

由式（13），改变两ESOPS在谐振腔内传输一周的相位差，得到谐振曲线。取仿真参数如下：kc=0.1，αc=0.2 dB，εt=25 dB，θt=3∘°，εk=23 dB，θk=4°，l=1.8 m，不同相位差下谐振曲线仿真结果如图2所示。

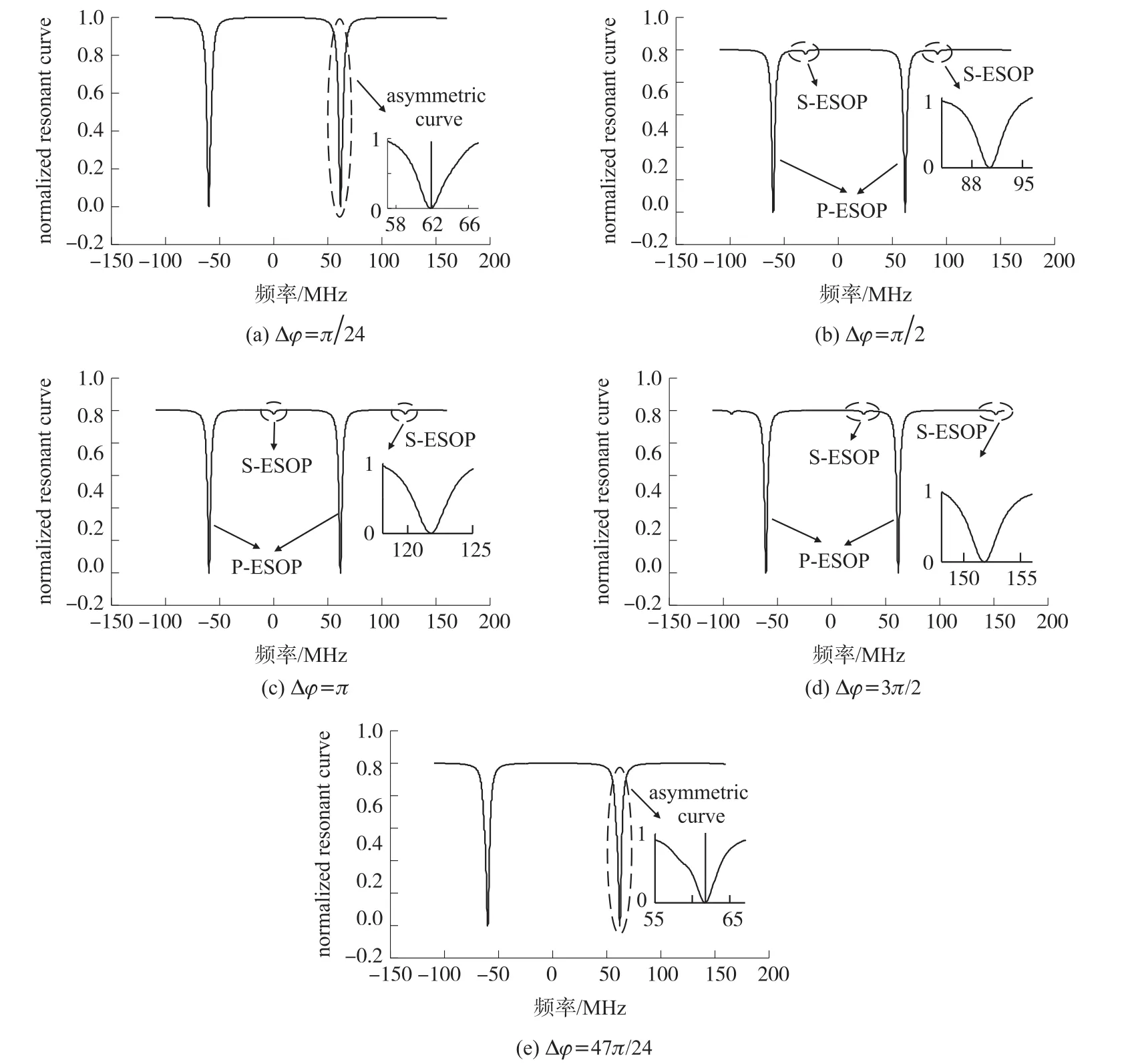
图2 不同相位差下谐振曲线仿真结果

如图2所示，两ESOPS的相位差为π/24时，二者相距较近，P-ESOP扭曲失真比较严重，半高全宽（FWHM）增加。此时P-ESOP对FRR温度的改变十分敏感，任意微小的温度扰动都将引起谐振曲线变形加重。相位差Δφ增加到π/2、π时，S-ESOP逐渐向P-ESOP右侧移动，其对主偏振态谐振的干扰作用逐渐减弱，偏振波动噪声引起的谐振频率漂移量相对减小；当Δφ继续增加到3π/2，47π/24时，S-ESOP由左侧逐渐靠近P-ESOP。采用光纤偏振控制器获得所需的任意偏振态输出光，测得双折射率差温度系数为2.39×10-7/℃，当相位差变化π时，FRR温度约变化2℃。可见，温度引起的偏振波动噪声存在周期性。且当两ESOPS的相位差为π时，二者相距最远，偏振波动噪声产生的影响最小。由两ESOPS谐振频率差可知，当Δφ=π时，fd=FSR/2。如图中（a）所示，两ESOPS相距较近时，FRR谐振曲线线形表现出严重不对称性，FWHM增大。这种不对称性，第一，影响谐振输出特性。对于腔长一定的FRR，其自由谱宽FSR是一个定值。由（14）式可知，随着FWHM的增大，谐振腔精细度降低，谱线质量变差。

第二，谐振曲线对其上每一频率点求导可得到解调曲线，故谐振曲线不对称性可能会影响解调曲线线性度以及解调曲线线性区斜率的大小，二者均为评估解调曲线优劣的重要指标［11-13］。根据（15）仿真不同相位差下的解调输出，如图3所示。

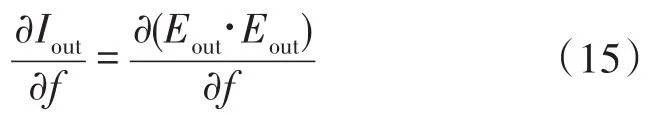
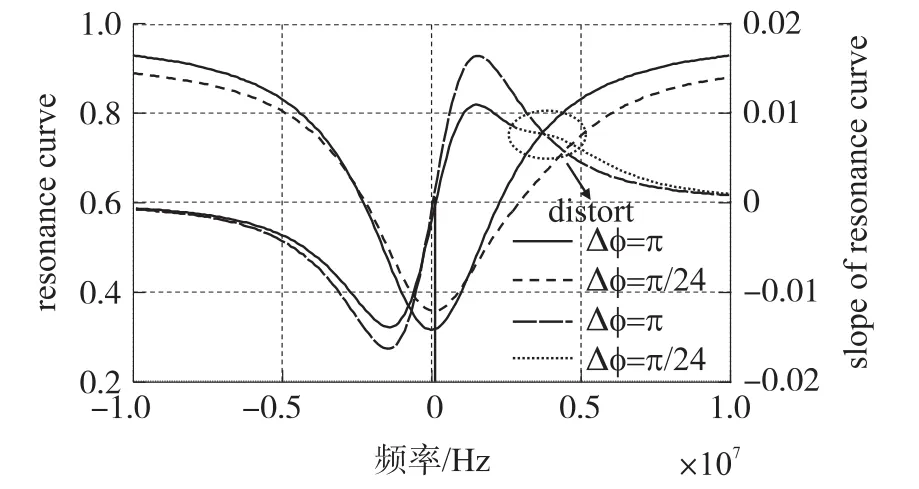
图3 不同相位差下解调曲线仿真结果

图3中黑色虚线和实线分别表示两ESOPS相位差为π/24和π时的同步解调曲线，对应的谐振曲线如图中蓝色虚线和实线所示。可见，当谐振曲线不对称时，对应的解调曲线扭曲，线性区斜率减小；解调曲线零点发生偏移，P-ESOP谐振频率点检测产生误差，即谐振频率漂移。该漂移量由S-ESOP谐振引入的干扰造成，等效在输入端构成非互易性频差Δf，影响静态下R-FOG输出。

为估算偏振波动噪声引起的非互易性频差Δf，采用洛仑兹函数近似表示两ESOPS在谐振腔输出端口的光波场，分别为：

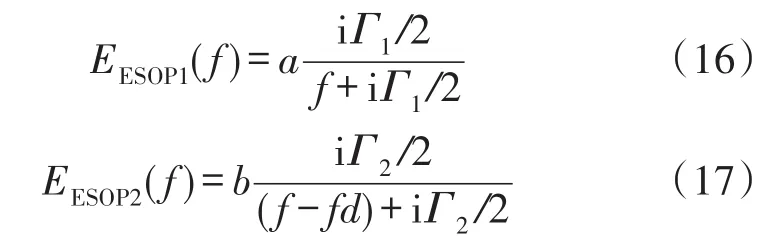
谐振腔总输出光强为：

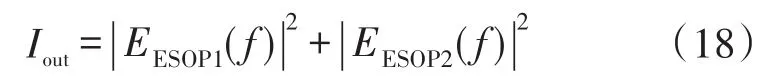
式中，Γ1、Γ2分别为两ESOPS对应谐振曲线的半高全宽。将P-ESOP在CW方向的谐振频率漂移记作Δfcw，由，求得Δf为：

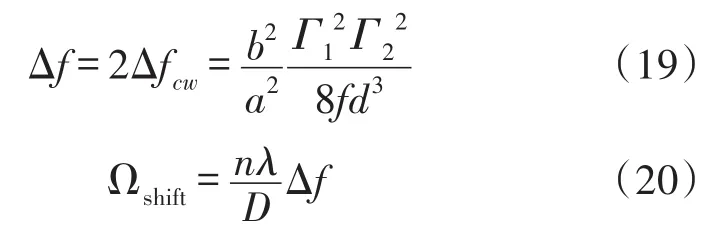
由式（19）～式（20）可知，静态下R-FOG输出发生零偏，零偏大小与两ESOPS幅值之比b/a及Γ1、Γ2成正比；与fd成反比。当fd足够小，导致谐振曲线不对称时，R-FOG输出零偏较大；此时，由于S-ESOP距离P-ESOP较近，两ESOPS对FRR温度变化非常敏感，外界微小的温度扰动都将引起较大的R-FOG零偏漂移，零偏稳定性降低，R-FOG精度恶化。

为了减小谐振曲线不对称对R-FOG零偏和零偏稳定性的影响，两ESOPS的谐振谷位置应尽量远离，将这些状态对应的FRR温度设定为工作温度时，S-ESOP对P-ESOP谐振的干扰较弱，系统受到的偏振波动噪声的影响最小。

2 实验与结果

为了对FRR进行主动温度控制，文中首先设计并搭建了温控执行系统，如图4所示。该系统中各器件的安放顺序自下而上为散热片、热电制冷器TEC（Thermoelectric Cooler）、铝片、FRR、热敏传感器。温控器（TCM）的温控精度可达到±0.01℃，实验前将其连接到温控执行系统外部。系统开始工作后，热敏传感器将探测到的FRR温度信息传递给TCM，通过对比实际温度和设定温度之间的差异，并将温度差值信号作用到TEC制冷器上，TCM就可以将FRR环境温度调整到预先设定的温度值，以达到控温的目的。各器件之间的空隙用导热硅脂均匀填充，最外层用隔热材料制成的保温盒子罩住，以隔绝温控执行系统与外界的热量传递。温控执行系统搭建的合理与否，直接影响着谐振腔温度响应特性的准确程度。

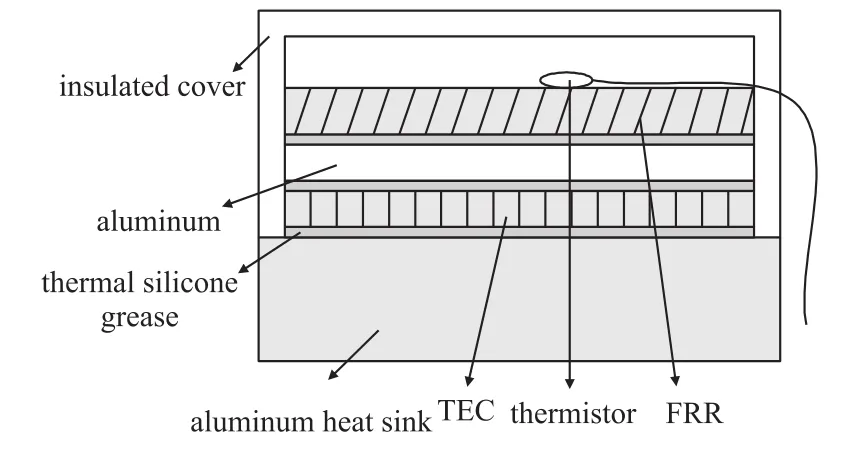
图4 温控执行系统

2.1 谐振曲线的温度特性测试

实验中采用的是保偏反射式谐振腔及保偏定向式耦合器。不包含耦合器长度，FRR腔长为1.8 m，耦合器插入损耗0.2 dB，耦合系数为0.1。由于R-FOG室内环境工作温度大约为 25℃，故选择22.00℃～31.00℃作为FRR实验温度范围，且每间隔0.5℃测试一组FRR谐振输出曲线。选出其中描述S-ESOP位置相对P-ESOP发生明显变化的标志性温度点对应的谐振曲线，如图5所示。图中用箭头标记出了两ESOPS。由图可见，随着FRR温度的增加，S-ESOP谐振谷的位置由P-ESOP的左侧逐渐移动到右侧。当FRR温度为25.50℃时，两ESOPS的谐振谷间距较近，如（b）中局部放大图所示，谐振曲线关于谐振频率点左右不对称，曲线整体发生扭曲变形。FRR温度为27.00℃时，S-ESOP幅度较小，位置大约在FSR/2处，对应的相位差Δφ=π，结合前面的理论分析可知，此时两ESOPS相距最远，P-ESOP谐振曲线关于谐振点对称，如（d）中所示。当FRR温度继续升高到28℃、30.50℃时，S-ESOP再次由左侧逐渐靠近P-ESOP，如（e）、（f）图所示。实验结果验证了理论分析。经计算，FRR温度为24.50℃时，谐振腔FWHM值为3.85 MHz，对应的精细度F为32.5；当FRR温度变为25.50℃时，FWHM值增加到4.93 MHz，精细度下降为25.4，可见，谐振曲线不对称会导致谱线的尖锐度和质量变差。

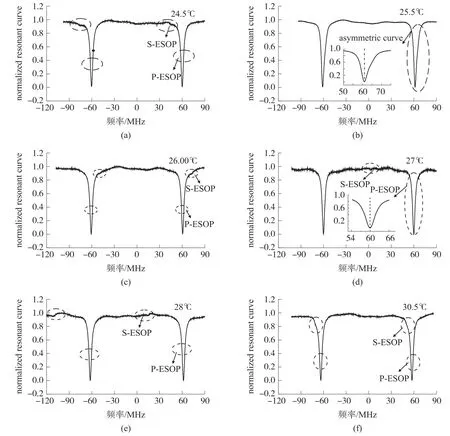
图5 不同FRR温度下谐振曲线实验结果

2.2 解调曲线的温度特性测试

FRR温度为27.00℃和25.50℃时谐振曲线对应的同步解调输出如图6所示。计算得出FRR温度为27.00℃时，解调曲线线性区斜率为0.39 V/MHz；FRR温度为25.50℃时，线性区斜率为0.28 V/MHz。结合图5可知，当谐振曲线不对称时，其对应的解调曲线扭曲，线性区斜率减小，R-FOG检测灵敏度降低。与此同时，温度为25.50℃时的解调曲线零点发生明显偏移现象，频率偏移量绝对值约为0.3 MHz，最终导致系统产生谐振频率点检测误差。当FRR温度为27.00℃时，相比其他温度状态，解调曲线斜率较大，零点偏移较小，S-ESOP干扰最弱。

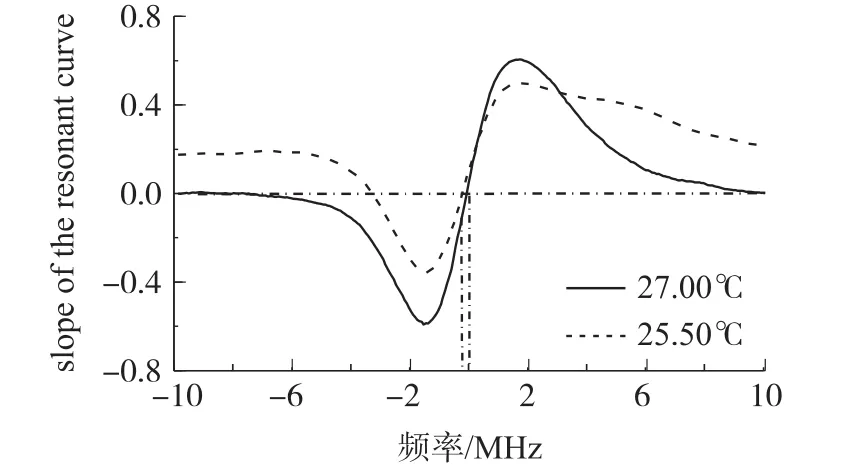
图6 不同FRR温度下解调曲线实验结果

2.3 陀螺的温度特性测试

在静止状态下对R-FOG输出进行测试，积分时间为1 s，采样时间为150 s。图7给出了FRR温度分别为22.00℃、25.00℃、25.50℃、27.00℃以及30.50℃时，各温度状态对应的R-FOG零偏和零偏稳定性测试结果。

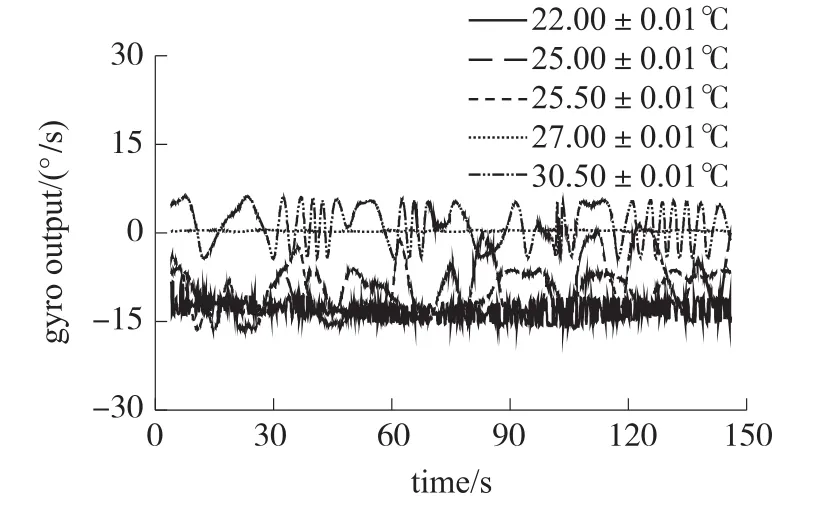
图7 FRR温度与R-FOG零偏和零偏稳定性的关系

从图7可以看出，FRR温度不同时，陀螺零偏各不相同；当FRR温度基本一定，且在该温度附近保持±0.01℃的微小温度扰动时，各温度状态对应的零偏稳定性存在着很大差异。FRR温度为25.50℃时，对150 s内的输出初始采样数据求标准方差为2.6 mV，根据该温度下标定过的解调曲线线性区斜率0.28 V/MHz，可求得等效Sagnac频差为9.286 kHz，R-FOG零偏稳定性约为6.69°/s。零偏约为-5.10 °/s，系统检测精度较低；将FRR温度控制到27.00℃时，对R-FOG输出数据求标准方差，其值为0.38 mV，根据解调曲线线性区斜率0.39 V/MHz求得等效Sagnac频差为0.97 KHz，零偏稳定性为0.07°/s，陀螺输出无明显漂移，且零偏约为0.21°/s；将FRR温度升高到30.50℃时，输出标准方差为1.6 mV，等效Sagnac频差为4.4 KHz，零偏稳定性为3.2°/s。

结合前面的分析可知：FRR温度为25.50℃时，两ESOPS相位间隔最近，S-ESOP谐振引起了P-ESOP谐振谷的不对称。在该温度下测得的R-FOG输出零偏为-5.10°/s，零偏稳定性为6.69°/s，零偏漂移较大，R-FOG检测精度较低；FRR温度为27.00℃时，两ESOPS相位差为π，距离最远，此时P-ESOP受S-ESOP干扰最小，测试R-FOG输出零偏为0.21°/s，零偏稳定性为0.07°/s，该值近似等于温度为25.50℃时的1/100。其余各温度状态下的陀螺零偏及零偏稳定性介于25.50℃与27.00℃之间。可见，R-FOG静态输出零偏、零偏稳定性由S-ESOP对P-ESOP谐振的干扰程度决定。为提高R-FOG静态指标，改善S-ESOP干扰引起的谐振曲线不对称性显得十分必要。

3 结论

本文采用了对FRR进行主动温度控制的方法，测试了不同FRR温度下的谐振曲线、解调曲线以及R-FOG零偏和零偏稳定性。实验结果显示：在R-FOG室温工作环境下，将 FRR温度控制到27.00℃附近时，两ESOPS相位差为π，谐振频率差约为|FSR/2|，系统受偏振波动噪声影响最小，R-FOG的零偏稳定性在150 s的采样时间内为0.07°/s，该值近似等于25.50℃时的1%，短期内系统输出无明显漂移。结果表明：FRR环境温度变化引起的两ESOPS相对位置的改变，为R-FOG引入了偏振波动噪声；当二者间距较小时引起谐振曲线不对称，谐振频率点检测产生误差，R-FOG输出发生零偏及零偏波动现象，系统检测精度降低。相比国内外已有的研究成果，本文更侧重于探究FRR温度变化对R-FOG整体性能的影响。FRR最佳工作温度的选择和控制对于减小R-FOG中的偏振波动噪声以及提高系统的检测精度有着重要意义。

［1］陈妍.双路闭环谐振式集成光学陀螺研究［D］.浙江：浙江大学，2012.

［2］姚灵芝，马慧莲，金仲和，等.基于单片FPGA的谐振式光纤陀螺数字系统设计与实现［J］.传感技术学报，2011，24（9）：1260-1264.

［3］杨远洪，孟晨雪.光纤陀螺零偏误差特性及噪声分析方法研究［J］.光学学报，2014，34（12）：1206006-1-1206006-2.

［4］陈旭光，杨平，陈意，等.MEMS陀螺仪零位误差分析与处理［J］.传感技术学报，2012，25（5）：628-632.

［5］Sanders G A，Smith R B，Rouse G F.Novel Polarization-Rotating Fiber Resonator for Rotation Sensing Applications［J］.Fiber Optic And Laser Sensors VII，1989，1169：373-379.

［6］Watsuki K，Hotate K，Higashiguchi M.Eigen-State of Polarization in a Fiber Ring Resonator and Its Effect in an Optical Passive Ring-Resonator Gyro［J］.APPL OPTICS，1986，25（15）：2607-2608.

［7］Wang X J，Jin Z H，Hotate K.Reduction of Polarization-Fluctuation Induced Drift in Resonator Fiber Optic Gyro by a Resonator with Twin 90°Polarization-Axis Rotated Splices［J］.Optics Express，2010，18（2）：1677-1683.

［8］Ma H L，Yu X H，Jin Z H.Reduction of Polarization-Fluctuation Induced Drift in Resonator Fiber Optic Gyro by a Resonator Integrat ing In-Line Polarizers［J］.Optics letters，2012，37（16）：3342-3344.

［9］张旭琳，马慧莲，金仲和，等.谐振式光纤陀螺中偏振波动的影响［J］.传感技术学报，2003，16（2）：150-154.

［10］Yu X H，Ma H L，Jin Z H.Improving Thermal Stability of a Resonator Fiber Optic Gyro Employing a Polarizing Resonator［J］.Optics Express，2013，21（1）：358-369.

［11］Ying D Q，Li Q，Ma H L，et al.Residual Intensity Modulation in Resonator Fiber Optic Gyros with Sinusoidal Wave Phase Modulation［J］.Journal of Zhejiang University Science C，2014，15（6）：482-488.

［12］李小枫，郑永秋，安盼龙，等.调相谱检测技术下光纤环腔的谐振特性［J］.红外与激光工程，2014，43（10）：3395-3396.

［13］焦新泉，郑永秋，安盼龙，等.谐振式光纤陀螺双光路调相谱最优参数确定方法［J］.红外与激光工程，2015，44（1）：240-242.

张 婷（1990-），女，硕士，2014年中北大学仪器与电子学院仪器仪表工程专业学习，主要从事微纳光纤传感方面的研究，1170303911@qq.com；

薛晨阳（1971-），男，教授，博士生导师，博士，主要从事传感器技术、微纳器件方面的研究工作，xuechenyang@nuc.edu.cn。

Temperature Characteristics of Polarization Fluctuation Noise in Resonator Fiber Optic Gyroscope*

ZHANG Ting，ZHENG Hua，DU Jiangong，AN Panlong，YAN Shubin，XUE Chenyang*
（Science and Technology on Electronic Test&Measurement Laboratory，North University of China，Taiyuan030051，China）

Polarization fluctuation owing to temperature variations of the fiber ring resonator（FRR）is one of the main optical noises，which seriously affects detection accuracy of resonator fiber optic gyroscope，it can be effectively suppressed by controlling temperature of resonator.In order to suppress polarization fluctuation to reduce the deterioration of R-FOG accuracy caused by temperature changes of FRR，the effect of temperature variations on resonance curve and demodulation curve were theoretically analyzed in this paper.Experiments to research resonant characteristics and demodulation curve features and zero bias and zero bias stability at the gyro output were carried out under different temperatures，and experimental results were analyzed.Results show that by controlling the temperature around the fiber ring resonator to 27.00℃，phase separation between the unwanted resonance and the desired resonance achieves farthest，the desired resonance is primly symmetrical about the resonant frequency point，slope of the linear region on demodulation curve reaches its maximum，detection error of resonant frequency can be ignored in this state；a zero bias stability of 0.07°/s of gyro is obtained in sampling time of 150 s，which is almost 100 times small than that when the temperature of resonantor is 25.50℃，detection accuracy of gyro is markedly improved.

R-FOG；polarization fluctuation；temperature controlling；zero bias stability；fiber ring resonator

TN91

A

1004-1699（2016）12-1815-07

��4140；7230E

10.3969/j.issn.1004-1699.2016.12.006

项目来源：国家自然科学基金杰出青年基金项目（51225504）

2016-05-16修改日期：2016-06-07