南海深水钻井平台锚泊系统预张力优选研究

郑纯亮， 陈国明， 张 浩， 罗 宁， 刘正礼

(1.中国石油大学(华东) 海洋油气装备与安全技术研究中心， 山东 青岛 266580； 2. 中海石油(中国)有限公司深圳分公司， 广东 深圳 518067)

南海深水钻井平台锚泊系统预张力优选研究

郑纯亮1， 陈国明1， 张 浩1， 罗 宁1， 刘正礼2

(1.中国石油大学(华东) 海洋油气装备与安全技术研究中心， 山东 青岛 266580； 2. 中海石油(中国)有限公司深圳分公司， 广东 深圳 518067)

根据不同工况对锚泊系统的不同要求，确定锚泊系统性能优化的设计变量、优化目标和约束条件等。以南海某深水半潜式钻井平台为例，采用ANSYS-AQWA软件建立平台-锚泊系统动力耦合分析模型，根据现场环境载荷划分工况，并采用AQWA-DRIFT模块进行时域分析，得到各个方向上平台的最大漂移量、平均漂移量及系泊线最小安全系数等结果。基于作业工况安全作业窗口最大的优化要求，以及现场对平台漂移量和系泊线安全性能要求的优先级顺序，确定作业工况下的最优预张力范围；选取某极限工况，基于极限工况系泊线安全系数最大的优化要求，确定极限工况最优预张力范围。

锚泊系统；优化要求；工况；预张力；优选

0 引言

随着我国南海油气勘探开发水域日趋加深，对半潜式钻井平台的需求逐渐增加。锚泊定位为我国南海半潜式钻井平台的重要定位方式，而锚泊系统的预张力设置对保证深水锚泊系统的安全作业十分重要。预张力过大则系泊线动张力大，不利于平台安全；预张力过小则平台漂移量大，不能满足正常作业要求。我国南海工况复杂，不同工况对平台锚泊系统的要求也不同，因此预张力的选择原则也不同。尤其在我国南海海域环境恶劣，恶劣的环境条件极易引发一系列锚泊系统失效事故。从实际出发，结合现场作业要求研究不同工况下深水锚泊系统的预张力优选很有必要。

锚泊系统的优化方面，国内外学者进行了大量地研究。Mehdi Shafieefar[1]基于遗传算法提出一种可以使平台响应最小的锚链布局和锚链张力优化自动程序。Rio de Janeir[2]利用遗传算法优化布锚方案使平台漂移量最小。金鸿章等[3]利用改进的遗传算法优化系泊线张力。樊磊等[4]以满足安全校核及水动力性能良好为目标，采用时域方法对半潜式起重平台的系泊系统进行优化研究。这些研究丰富了锚链系统设计方法，然而由于锚泊系统影响因素多，不同工况对锚泊系统的要求不同，目前的研究成果不能适用于所有工况形成统一的优化方法，研究成果与现场应用的结合需进一步加强。

该文的研究面向我国南海深水油气开发实际，结合现场平台锚泊系统参数和环境数据，分析不同工况下锚泊系统的力学响应性能，并对锚泊系统的预张力进行优选，为深水锚泊系统的安全作业提供技术支持。虽然多种因素对平台-锚泊系统的水动力响应都有影响，但是作业工况和极限工况下的预张力优选思路不变，该文在作业水深、平台外形、锚泊系统布置方案等确定的前提下研究预张力优选方法，符合工程要求。

1 锚泊系统性能优化要求

1.1 优化表达式

锚泊系统的预张力优化属于多目标优化问题[5]，多目标优化问题的数学表达式为[6]：

设计变量：

目标：

约束：

式中：ai、bi为第i个设计变量xi的上下限；n为设计变量的个数；p为非上、下限等式约束的个数；l为非上、下限不等式的约束个数。

1.2 设计变量

锚泊系统力学性能的影响因素很多，但是现场作业过程中很多因素是不可调整的，如锚泊系统的类型、设备选型、系泊线成分等内部因素是作业前提前设定好的，而环境载荷等外部因素是不可控的，锚泊方案中的布锚角度、抛锚位置等一旦抛锚完成也很难调整，而最容易调整也最符合实际的因素就是出缆长度，即通过调整出缆长度控制预张力，因此，锚泊系统性能优化的设计变量为系泊线出缆长度/预张力。

1.3 优化目标

作业过程中调整锚泊系统预张力不但影响作业效率，造成大量经济损失，而且在系泊线张力比较大的情况下调整锚泊系统存在风险，绞车刹车或者止链器可能导致严重的破坏。同时，即使有些预张力调整出现在操作手册中，但是很少执行，因此，作业过程中不建议调整预张力，除非很有必要执行并且应在保证平台安全的前提下操作。故认为作业工况的预张力一旦设定好，工况改变时不再调整，预张力方案应尽量满足多种环境条件要求，即作业工况预张力的优化目标为安全作业窗口最大。

由于极限工况下不再作业，因此对平台漂移量不再要求。极限工况下通常断开隔水管连接，放松锚链，保证锚泊系统在台风等极端载荷下不受损，尽量提高系泊线的安全系数(系泊线破断张力/系泊线最大张力)。放松锚链的程度应根据气象预报的极限工况载荷大小确定，优选极限工况预张力时，应首先比较所有锚链的最小安全系数，保证最危险锚链的安全；当最小安全系数接近时，应进一步比较平均张力的大小，平均张力越小，锚泊系统越安全，即极限工况预张力的优化目标为系泊线安全系数最高。

通常情况下，预张力越大对控制平台漂移量越有效，预张力越小对保证系泊线安全越有益。不同的工况条件下对平台的要求不同，在优选预张力时需要判断控制平台漂移量和保证系泊线安全性能的优先级，根据现场需求适当调整优化目标。

1.4 约束条件

深水半潜式平台锚泊系统主要用于定位，为保证顺利地进行钻井作业，要求平台漂移量不超过规定范围。为保证锚泊系统的结构和功能的完整性，要求系泊线不发生断开，通常要求系泊线张力的最小安全系数不大于许用值，此外，要求锚泊系统不发生走锚、疲劳失效等。走锚的影响因素很多，走锚不一定意味着事故。该文分析对象属于移动式系泊，疲劳失效分析不是重点，故分析过程中不考虑走锚和疲劳，锚泊系统性能优化的约束条件为平台漂移量和系泊线张力满足作业要求，平台漂移量和系泊线张力的要求参考API-RP-2SK标准[7]。综合考虑，认为作业时平台的平均漂移量不应超过水深的4%，最大漂移量不应超过水深的8%，锚泊系统完整条件下动力分析的系泊线最小安全系数不应小于1.67。

综上所述，该文锚泊系统力学性能优化以预张力为控制变量，作业工况安全作业窗口最大、极限工况系泊线安全系数最大为优化目标，平台漂移量和系泊线张力满足作业要求为约束条件，优选出作业工况和极限工况的最优预张力。

2 分析模型及方法

2.1 分析模型

该文以南海某半潜式钻井平台为研究对象，其锚泊系统为8点、45°对称分布的移动式系泊系统，工作水深631 m，系泊线为锚链和锚缆的组合形式，底端与锚连接的卧底段为锚链，上端与平台连接段为锚缆，中间过渡段为锚链。

采用ANSYS-AQWA软件建立锚泊系统的水动力分析模型，建立的平台ANSYS模型如图1所示，整个模型的湿表面采用Shell63单元，撑杆采用Pipe59单元进行网格划分。将ANSYS模型数据导入到AQWA中，定义水深、系泊线、导缆孔、锚点、重心等信息，得到无隔水管的平台-锚泊系统耦合分析模型，如图2所示。

图1 南海某平台ANSYS模型

图2 无隔水管平台-锚泊系统耦合模型

为方便计算分析，模拟过程进行了如下简化：

(1) 不考虑锚土的相互作用，认为锚点是一个刚性节点，即认为不发生走锚。

(2) 忽略锚泊系统中因腐蚀、磨损等原因造成的各组件刚度、断裂强度的降低。

(3) 风荷载和流荷载计算采用恒定风和恒定流理论。

(4) 风、浪、流方向一致，即各个方向环境载荷为风浪流的最大组合，这是一种偏保守的简化。

(5) 不考虑系泊线弹性伸长，认为系泊线长度恒定。

2.2 分析方法

锚泊分析中常采用的方法包括准静定法、频域法、时域法。准静定法由于计算过程简单，可用于移动式系泊和安全性较高的永久式系泊的初步分析。频域法计算简单，但是需要对非线性问题进行处理，常用于锚泊系统的运动机理研究。时域法可解决稳态问题、瞬态问题和非线性问题，可模拟动力响应的时间历程，但是该方法计算量大、耗时长。三种分析方法可以分别通过AQWA中的Cable Dynamics、AQWA-FER、AQWA-DRIFT模块实现。由于时域法的计算结果准确性相对较高，且采用AQWA软件计算速度快，因此，该文计算主要基于AQWA-DRIFT模块进行时域分析。

3 作业工况预张力优选

3.1 工况划分

根据现场某区块的环境参数定义分析工况，具体细化见表1。其中，工况1为1年重现期季风工况，工况4为1年重现期台风工况。

表1 分析工况细化表

3.2 分析计算

分别设定锚泊系统预张力为129 t、137 t、156 t，在此基础上进行锚泊系统动力分析，得到不同环境入射方向下的平台漂移量和系泊线动张力的时历结果，进一步整理得到平台的最大漂移量、平均漂移量及系泊线的最小安全系数。以工况1预张力137 t为例，得到各个方向上平台的最大漂移量、平均漂移量及系泊线的最小安全系数，如图3～图5所示。

图3 工况1 预张力137 t时平台平均漂移量

图4 工况1 预张力137 t时平台最大漂移量

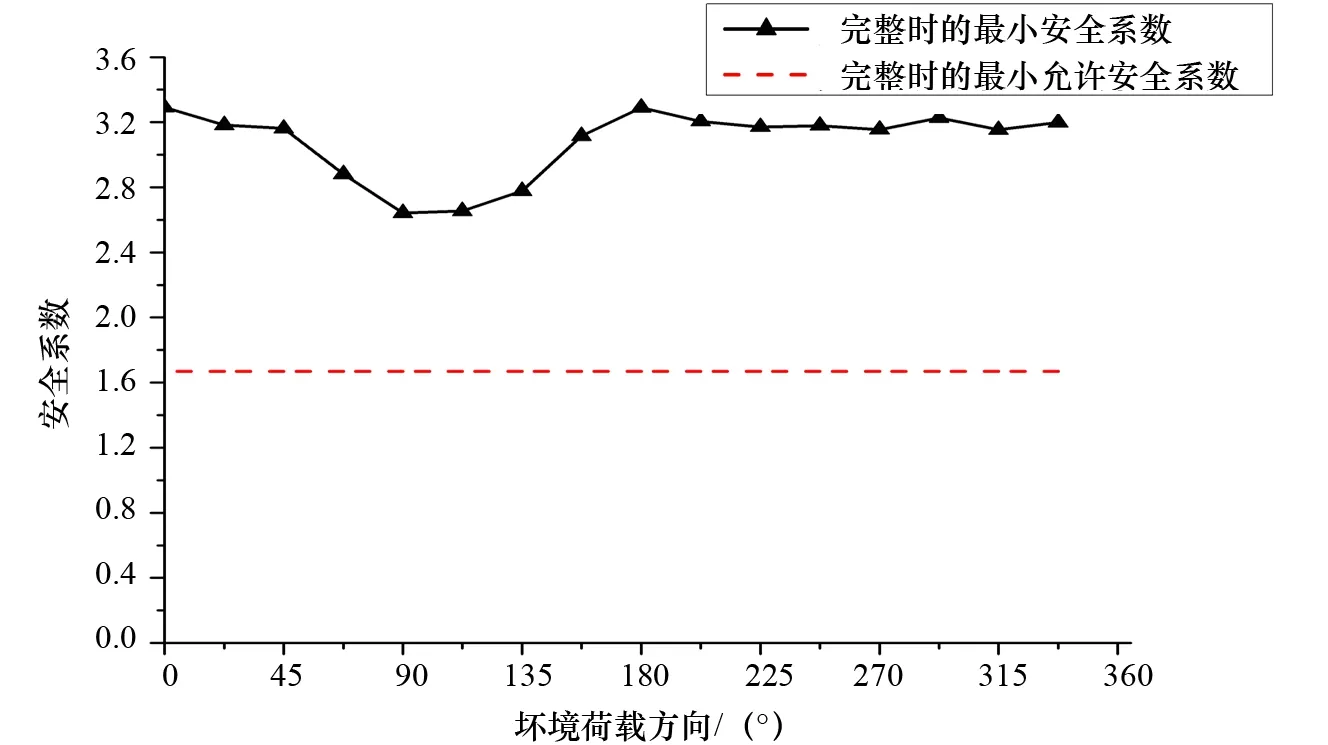
图5 工况1 预张力137 t时系泊线最小安全系数

3.3 预张力优选

根据1.4节所述约束条件及平台所在海域水深，确定平台允许平均漂移量为25.24 m，允许最大漂移量为50.48 m，允许系泊线最小安全系数为1.67。综合这三条约束条件，统计不同工况、不同预张力下，平台平均漂移量、最大漂移量、系泊线最小安全系数在各个方向上的最大值及其许用值，如图6～图8所示。

图6 预张力129 t时各工况下最大漂移量与最小安全系数

图7 预张力137 t时各工况下最大漂移量与最小安全系数

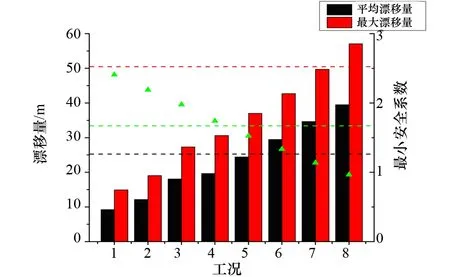
图8 预张力156 t时各工况下最大漂移量与最小安全系数

通过对比可以发现，预张力129 t、137 t、156 t时的作业窗口都为工况1～工况4。预张力为129 t时，在工况4下平台漂移量接近允许值，预张力156 t时，在工况4下系泊线张力接近允许值。如果预张力比129 t小，容易出现平台漂移量超过允许值的情况；同样，如果预张力比156 t大，容易出现系泊线最小安全系数低于允许值的情况。这两种情况都会缩小作业窗口，因此，认为预张力在129 t～156 t之间，锚泊系统的安全作业窗口最大，即作业工况最优预张力在该范围内。

在预张力129 t～156 t之间选取最优预张力，需要首先判断现场对平台漂移量和系泊线安全性能要求的优先级。如果现场对平台漂移量要求更为严格，则最优预张力为156 t左右；如果现场对系泊线的安全性能更看重，则最优预张力为129 t左右；如果不确定二者优先级，或二者要求折中，选取最优预张力为137 t左右。

4 极限工况预张力优选

4.1 工况确定

极限载荷来临前需要减载、减少吃水，同时放松锚链，不同极限工况下锚链的放松程度应有所区别，需根据预报载荷大小优选特定极限工况下的最优预张力。通过3.3节发现，工况5超出安全作业的要求范围，因此，认为工况5为最小的极限工况，以工况5为例，优选该极限工况下最优预张力。

4.2 分析计算

分别设定锚泊系统预张力为40 t、50 t、70 t、86 t、112 t，在此基础上进行锚泊系统动力分析，得到不同环境入射方向下，系泊线动张力的时历结果，进一步整理得到系泊线的最小安全系数。极限工况不同预张力条件下的最小安全系数计算结果见表2。

表2 极限工况系泊线完整时不同预张力下最小安全系数统计表

注：表中“[]”数字代表安全系数最小的系泊线号。

根据表2数据，分别绘制不同预张力下锚泊系统的最小安全系数的图像，如图9～图13所示。

图9 预张力40 t时系泊线最小安全系数

图10 预张力86 t时锚泊系统的最小安全系数

图11 预张力50 t时系泊线最小安全系数

图12 预张力112 t 时系泊线最小安全系数

图13 预张力70 t时系泊线最小安全系数

4.3 预张力优选

通过对比发现，当预张力取86 t 和112 t时，基本可以保证锚泊系统的安全要求。当台风荷载来临后，平台将产生迅速的张力骤增，然后再回到某一平衡位置呈现振荡现象。根据图14、图15统计500 s以后两条系泊线的平均动张力，结果见表3。

根据表3可以看出，预张力112 t时，2号系泊线在产生张力骤增现象后，重新进入张力平衡状态下的平均动张力比预张力86 t 时大，考虑到系泊线的疲劳破坏问题，应尽量降低系泊线的平均动张力。对比其他环境入射方向上张力稳定以后的各主要受力系泊线的平均动张力，发现其规律与上述内容相符。在保证相同安全系数条件下，应选用86 t预张力作为平台在极限工况下的预张力。因此，该极限工况下的最优预张力为86 t左右。

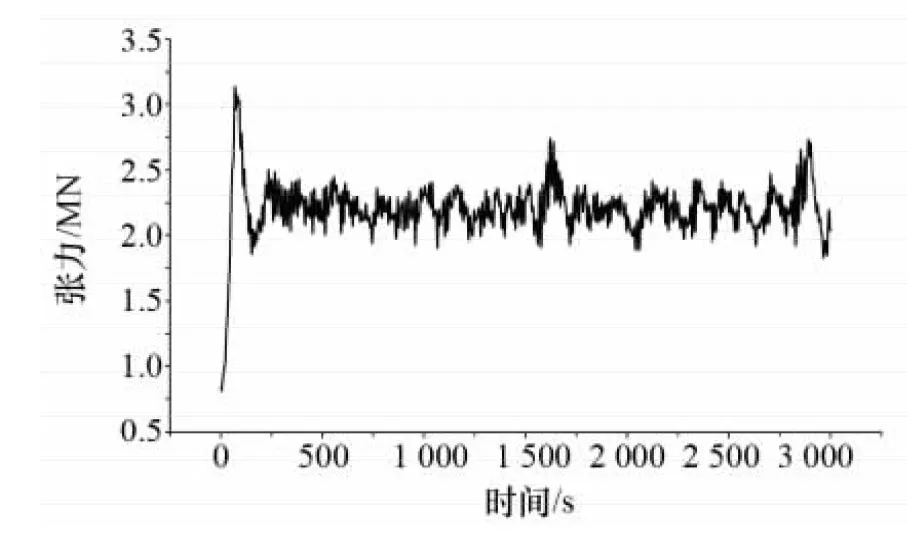
图14 预张力86 t时，环境入射角为90°时2号锚动张力曲线

图15 预张力112 t时，环境入射角为90°时2号锚动张力曲线

表3 环境入射角90°，2号系泊线在不同预张力条件下的平均动张力对比表

5 结论

(1) 优选作业工况下锚泊系统预张力，发现预张力在129 t～156 t时，锚泊系统的安全作业窗口最大。优选最优张力需要确定平台漂移量和系泊线安全性能要求的优先级。如果现场对平台漂移量要求更为严格，则作业工况下最优预张力为156 t左右；如果现场对系泊线的安全性能更看重，则最优预张力为129 t左右；如果不确定二者优先级，或二者要求折中，则最优预张力为137 t左右。

(2) 以某极限工况为例，优选极限工况下锚泊系统的预张力，发现预张力在86 t和112 t锚泊系统的安全性能最高，而预张力112 t下动张力大，易发生失效。因此，认为该极限工况下的最优预张力在86 t左右。

(3) 优选预张力时应考虑锚泊系统影响因素及现场作业要求，保证作业工况下安全作业窗口最大，极限工况系泊线安全系数最大。在布锚前应进行详细地分析讨论，综合考虑作业时的水深、锚泊系统类型、设备选型、系泊线组分、外部环境载荷等因素，确定不同工况下最优的布锚预张力。

[1] Mehdi Shafieefar. Aidin Rezvani. Mooring optimization of floating platforms using a genetic algorithm[J]. Ocean Engineering,2007, 34(10): 1413-1421.

[2] Carbono A J J, Menezes I F M, Martha L F. Mooring pattern optimization using genetic algorithms[A]. 6th World Congress of Structural and Multidisciplinary Optimization[C]. Brazil:Rio de Janeiro,2005.

[3] 金鸿章,苏晓宇,于安才,等. 基于锚链切换的平台自动锚泊定位系统设计[J]. 电机与控制学报, 2014,18(5): 93-98.

[4] 樊磊,孙丽萍,王宏伟,等. 半潜式起重平台系泊系统设计与优化研究[J]. 海洋工程, 2015,33(1): 31-38.

[5] Carlos A. An updated survey of GA-based mufti-objective optimization techniques[J]. ACM Computing Surveys, 2000,32(2):109-143.

[6] Marler R T,Arora J S. Survey of Mufti-objective Optimization Methods for Engineering[J]. Structural and Multidisciplinary Optimization,2004, 26(6): 369-395.

[7] API-RP-2SK. Recommended Practice for Design and Analysis of Stationkeeping Systems for Floating Structures[S]. Washington: Institute A P, 1997.

Optimization on Mooring Pretention of Deepwater Drilling Platform in South China Sea

ZHENG Chun-liang1, CHEN Guo-ming1, ZHANG Hao1, LUO Ning1， LIU Zheng-Li2

(1.Offshore Oil and Gas Equipment and Safety Technology Research Center, China University of Petroleum(Hua Dong), Shandong Qingdao 266580, China; 2.China Petroleum(China) Co., Ltd, Shen-zhen branch, Guangdong Shenzhen 518067, China)

In order to provide the reference to mooring opreration for deepwater drilling, optimization method on mooring pretention under different operation condition is presened in this paper. Firstly, according to different demands on mooring system under different operation condition, mooring system optimization demands are determined, including design variables, optimization objective and constraints. Secondly, taking a deepwater semi-submersible drilling platform in South China Sea as example, coupled dynamic analysis model of platform-mooring system is established using the software ANSYS-AQWA, operation conditions are divided according to environment data on site, and time domain method is adopted using AQWA-DRIFT module, which result in maximum platform offsets, mean platform offsets and minimum mooring line safety factors at different environment direction. Thirdly, based on the optimization demand that safety operation window should be maximized and different priority demand on platform offset and mooring line safety performance on site, the optimum pretension scope under operation condition is determined. Taking a survival condition as example, based on the optimization demand that safety factors of mooring lines should be maximized, the optimum pretension scope under this survival condition is determined.

mooring system; optimization demand; operation condition; pretention; optimization

1001-4500(2016)06-0091-08

2015-07-24

郑纯亮(1988-)，男，工程师。

P751

A