维特比算法的一种室内地磁导航方法

楼喜中，方 俊，陟 力

(中国计量大学 信息工程学院，浙江 杭州 310018)

维特比算法的一种室内地磁导航方法

楼喜中，方 俊，陟 力

(中国计量大学 信息工程学院，浙江 杭州 310018)

惯性导航系统是目前室内定位和导航领域一项非常重要的技术，但是传统惯性导航系统中是利用算法融合地磁罗盘及陀螺仪等数据，进而提高相对位置的精度，但却无法修正已经产生的误差.所以传统惯性导航系统在内部构造复杂的室内很容易出现走错房间，穿越墙体等错误路径.为了解决这些问题，提出一种基于维特比算法的室内导航方法,利用自建室内地磁数字地图结合维特比算法，动态计算可能路径.利用维特比算法特性提高了输出路径的纠错能力，可有效排除错误路径的干扰.本导航方法能有效避免穿墙错误路径的出现，更加符合实际行走路径.试验结果表明，相对传统惯性导航系统，它在复杂室内环境下进入正确房间的准确率提高了23%.

惯性导航系统；维特比算法；地磁数字地图

导航技术俨然成为现代社会生活中一项非常重要的技术，近年来，关于室内导航的研究课题也越来越多.室内导航技术层出不穷，有基于无线电的导航技术，如WLAN导航[1]、RFID导航[2-3]、GPS导航[4-6]和超宽带定位技术等.但是这些导航技术前期的布置成本高，在室内极易因为建筑物的内部构造复杂从而造成信号干扰，产生误差.

近年来，惯性导航技术成为热点，它不需要大量布置成本，自主性强、抵抗外界干扰能力强等特点吸引众多学者和机构的研究.它有捷联惯导系统和平台式惯导系统[7].惯性导航系统是利用惯性元件来测量运动人体的加速度，经过积分和运算得到速度和位置，从而达到对运动人体的定位和导航.这种技术非常依赖精确的步长、航向值等信息的收集，同时通过卡尔曼滤波[8]和粒子滤波[9]等算法减小传感器带来的误差，提高步长等数据的精度.

上述传统的惯性导航方法都是基于硬件误差的减小和利用算法建立误差模型提高数据精度的方式提高导航准确性，但是在进入极易混淆的相邻房间的时候，受误差的影响，会产生进错房间等错误路径，并在后续的行走过程中发生穿越墙体的情况.本文通过对导航区域自建地磁数字地图，结合维特比算法，利用维特比算法中度量值计算判断路径可能性，抛弃无效路径的方式有效避免穿越墙体的路径产生.该方法结合惯性导航系统，提高导航系统的纠错能力.由仿真试验结果表明，相较传统惯性导航技术中依赖高精度数据完成导航，本文提出的方法作为辅助手段可有效避免穿越墙体等错误路径的产生.

1 基于维特比算法的室内导航

1.1 地磁数字地图

由于地磁是遍布在近地空间的，而且地磁的数值大小相对比较固定.虽然室内空间布局和内部构造会对地磁大小产生影响，但是我们在制作地磁地图的时候是将这些影响一起记录进去的.同时室内空间对地磁的影响也增加了地磁地图的磁场特征，有利于算法对路径的筛选.制作地磁数字地图具体步骤为：

1)利用惯性导航设备中的高精度磁传感器在室内划分好的网格点交点处收集磁场数据；

2)惯性导航设备在室内划分好的网格点交点处停留一段时间s，再将惯性导航系统中的磁场强度值截取中间若干个，若干个的磁场强度值组成一个集合M，从而计算出集合M的均值Ma=M/Ms，Ms表示集合M的个数；

3)惯性导航系统将得到集合M的均值Ma依次录入到磁场数据中的网格点交点中，从而完成自建立网格型的磁场数据库.如图1，其中地磁地图中X轴代表实际室内空间的长度，Y轴代表实际室内空间的宽度，Z轴代表实际室内空间磁场强度大小.数字地图中坐标(dx,dy,dz)中dz为二维平面位置(dx,dy)的磁场强度大小.dx表示X轴坐标，dy表示Y轴坐标.

图1 地磁数字地图示意图Figure 1 Magnetic field digital schematic map

1.2 维特比算法

维特比算法是一种在数字通信中经常使用的译码算法，于1976年由维特比(Viterbi)提出.作为隐马尔科夫模型[10]基本算法之一，维特比算法主要解决的问题就是在给定模型的情况下，在对应的观测值序列中找出最优状态序列[11].所以它是一种最优的动态规划算法，在众多路径当中找出最优路径，并且能够回溯输出整条路径.在本文中，将它应用在解决室内导航中，利用其寻找最优路径的特性，动态规划人体行走路径.

维特比算法完成动态规划的迭代计算过程如下：

(1)

(2)

δt(j)表示在观察时刻t正处在状态j产生出的路径的最大概率即度量值，Ψt(j)表示一个状态值，该值由上一状态计算产生.

同时我们还能回溯最优路径，回溯公式为

(3)

1.3 基于维特比算法的导航方法

本方法通过提供基础磁场数据计算每条可能路径的度量值，输出其中最大度量值对应的路径作为室内导航结果.

在传统惯性导航系统中，人行走的轨迹路径取决于人体航向值、步长和步数三个数据.其算法的基本原理如图2，(x0,y0)为行走起始点，(xi,yi)为行走的第i步点位置，H为人体行走航向值，航向值为绕Z轴旋转角度，初始角度为设备中默认值，S为步长.利用这些信息可以推算人体行走路径.

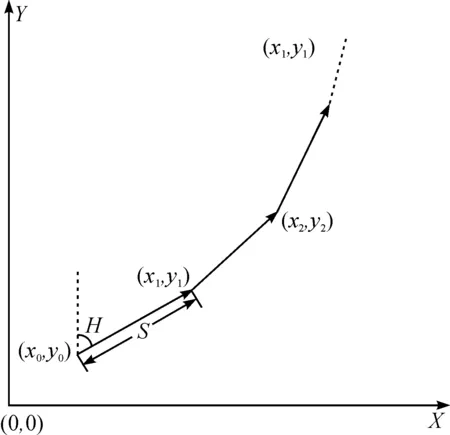
图2 传统惯性导航系统轨迹推算Figure 2 Traditional track estimate of inertial navigation

在此基础上的可能路径计算方式为：

1)根据人体航向值大小所在区间判断人体行走方向，因为仿真试验中使用的设备默认0°方向为正北，所以惯性导航系统中预设45°到135°为向东方向，135°到225°为向南方向，225°到315°为向西方向，315°到360°和0°到45°为向北方向.

3)依次计算可能位置，输出路径.因此可以实时计算出人体在行走过程中产生的所有可能路径.

图3 基于维特比算法惯性导航轨迹推算Figure 3 Inertial navigation track estimate base on Viterbi algorithm

图4 基于维特比算法导航示意图Figure 4 Navigation algorithm base on Viterbi algorithm

由此可以知道，如果一条可能路径偏离了实际路径，那么其地磁场序列和给定模型的序列误差增大，导致其度量值增大，这条错误的路径也就越容易被舍弃.而最贴近实际路径的可能路径会在排序中越来越高.为了防止可能路径计算中遗漏正确路径，导致最终偏离实际路线，出现进错房间，穿越墙体等错误路径出现，需要在算法中记录室内极易混淆的区域，如两个房间紧挨的区域.在此区域中，增加可能路径方向上的选择性，如图5.

图5 复杂区域可能位置选择示意图Figure 5 Select a possible location of complex regions

即保留前进方向上的下一位置点和与之垂直的方向上的相邻四个点，同时保留与路径前一位置相邻两点，共7个位置作为当前可能位置.

由于传统导航方法中，路径输出始终只有一条，一旦出现偏离现象，后面路径的规划会始终基于此错误路径之上，所以无法纠正自己的错误.但在本方法中，算法保留了正确路径，后面路径的规划会同时基于这些可能路径之上，进入正确房间的路径的排序会越来越高，同时错误路径将逐渐被舍弃.

此外，由于本导航方法中引入了地磁地图，可以将室内不可能到达区域的地磁强度设置为零，如墙体，柱体内部.当可能路径到达这些区域之后，当前位置的地磁误差会非常大，导致其度量值非常大，这条错误路径也会被舍弃.

错误路径的舍弃在算法中能够有效排除干扰，使后面可能路径的计算能够基于正确路径，输出最优结果.

2 仿真试验

为了保证试验数据的准确性，本文中使用的惯性导航模块是DRM4000L.制作相关室内空间的地磁数字地图方法如下：我们将导航模块绑在腰间，按照事先划分好的网格点，在上面停留一段时间s，点与点之间的距离设置为0.6米.为保证网格点上取到的地磁数据的准确性，我们停留5 s.将惯性导航模块设置为每0.5 s记录一次.因为开始检测地磁和结束时的移动可能会带来误差，所以我们只取中间的5组地磁数据，根据Ma=M/Ms计算得出当前网格点的地磁数据.依次记录，完成地磁数字地图的制作，如图6.

图6 地磁数字地图Figure 6 Magnetic field digital map

在仿真试验中，惯性导航系统中预设45°到135°为向东方向，135°到225°为向南方向，225°到315°为向西方向，315°到360°和0°到45°为向北方向，当初始位置A为(11,4)，同时在计算可能路径时，步数发生更新，根据人体航向值判断，A后的第一步为向东.此时在地图中，(11,3),(11,4),(11,5)都是第二步可能落下的位置，系统会记录可能路径，同时计算度量值.

为了验证本方法的性能，在测试时，测试人员的行走路线要尽量复杂，所以在试验中，要求测试人员按照Z字型行走.同时要求走进两个极易混淆的相邻教室，两个教室之间只有一道墙的距离.一共进行200组试验，分两种行走路线，其中100组的行走路线为(10,4)、(20,1)、(30,6)、(40,1)、(41,6)、(41,12)、(50,12).另100组的行走路线为(10,4)、(20,6)、(30,1)、(40,6)，(41,6)、(41,12)、(50,12).点与点之间按照直线行走.根据上面方法描述的特性，在行走过程中，惯性导航系统输出的原始路径若是发生穿墙行为是不会纠正自己的.但是本方法中，若发生穿墙行为，最终算法会自动抛弃错误的幸存路径，验证本方法的纠错能力.随着测试人员的行走，可能路径的数量会急速增加，需要设置合理的幸存路径条数，将其余路径排除.试验中各计算设置32、64、128、256、512条幸存路径的性能.

图7 仿真试验结果图Figure 7 Simulation results

通过上面的200组试验，传统惯性导航算法成功进入131次，成功率为65.5%.维特比算法的导航方法成功进入177次，成功率为88.5%.不同幸存路径最后正确率依次为51.5%，71%，88.5%，89.5%，90.5%.由于设置256条和512条幸存路径对最终准确率的提升并不明显，为了提高计算性能，选择128条幸存路径的试验结果作为最终试验结果.我们发现相较于传统惯性导航算法，基于维特比算法的导航方法在复杂室内环境下进入正确房间的准确率提高了23%.图7为其中一组试验仿真结果，由图7可以看出，惯性导航系统输出路径显示从走廊进入A教室后穿越墙体进入B教室，这是和图中实际行走路线不相符的错误路径.在两个相邻的教室中还是发生混淆.而度量值最大的可能路径区分出了两个教室，在仿真输出的幸存路径中也有走入A教室的，但是由于偏离实际路径，在后面的行走过程中逐渐被舍弃了.同时行走轨迹基本符合实际行走路线.有效克服传统导航系统中因为误差因素的影响进错房间并发生穿墙的情况，同时解决了传统惯性导航系统中只依赖精确步长和航向值等信息才能进行室内导航的缺点，提高室内导航纠错能力.

3 结 语

本文中所述的基于维特比算法的室内导航方法的优缺点如下所述.

优点：1)不严重依赖精确步长和航向值等信息；2)具有纠错能力，能够抛弃错误路径获得最优路径.

缺点：1)和实际路径之间的误差较大；2)路径方向改变不敏感.鉴于以上缺点，我们需要对本方法做进一步的改进，以便能够在实际工程应用中得到更广泛的运用.

[1] ZOU Han, JIANG Hao, LU Xiaoxuan, et al. An online sequential extreme learning machine approach to WiFi based indoor positioning[C]//2014 IEEE World Forum on Internet of Things (WF-IoT). Seoul: IEEE,2014:111-116.

[2] MILLER L E, BRYNER N P, FRANCIS M H, el al. RFID-assisted indoor localization and communication for first responders[C]//European Conference on Antennas & Propagation. Nice: IEEE,2006:1-6.

[3] 韩晶.基于RFID标签的定位原理和技术[J].电子科技,2011,24(7):64-67. HAN Jin. Position principles and location techniques based on RFID tags[J]. Electronic and Technology,2011,24(7):64-67.

[4] 李天文.GPS原理及应用[M].北京:科学出版社,2010:18-21.

[5] 施阁,卢江丽,孙延伟,等.航模动力及飞行环境无线实时监测系统设计[J].中国计量学院学报,2009,20(1):22-26. SHI Ge, LU Jiangli, SUN Yanwei, el al. Aeromodelling's power and flight environment wireless real-time monitoring system[J]. Journal of China University of Metrology,2009,20(1):22-26.

[6] 雷波,陈华德,李青,等.基于动态差分GPS的滑坡位移监测系统[J].中国计量学院学报,2011,22(63):203-207. LEI Bo, CHENG Huade, LI Qing, el al. Design of landslide displacement monitoring system based on dynamic differential GPS[J]. Journal of China University of Metrology,2011,22(63):203-207.

[7] TITTERTON D H, WESTON J L. Strapdown inertial navigation technology[J]. Aerospace & Electronic Systems Magazine IEEE,1997,20(7):33-34.

[8] GREWAL M S, ANDREWS A P. Kalman Filtering Theory and Practice Using MATLAB[M]. 3th ed.[S. 1.]: Circuit Theory & Design.2001:100-123.

[9] RISTIC B, ARULAMPALAM S, GORDON N. Beyond the kalman filter-particle filters for tracking applications[J]. IEEE Trans of Aerospace & Electronic Systems,2004,19(7):37-38.

[10] RABINER L. A tutorial on hidden markov models and selected applications in speech recognition[J]. Proceedings of the IEEE,1989,77(2):257-286.

[11] 刘功生,张春良,岳夏.基于HMM算法体系的逆维特比算法理论研究[J].机电工程技术,2014,43(11):7-10. LIU Gongsheng, ZHANG Chunliang, YUE xia. Research on theory of inv-viterbi algorithm based on the basic algorithm system of HMM[J]. M&E Engineering Technology,2014,43(11):7-10.

An indoor magnetic navigation method based on Viterbi algorithm

LOU Xizhong, FANG Jun, ZHI li

(College of Information Engineering, China Jiliang University, Hangzhou 310018, China)

The inertial navigation system is the most important technology of indoor navigation and positioning. The traditional inertial navigation system that uses the algorithm merge magnetic compass, gyroscopes and other data to improve the accuracy of a relative position can not correct the errors. Therefore, in a complex internal structure, it is easy to walk into a wrong room, walk through a wall and so on. In order to solve these problems, a kind of interior navigation method based on the Viterbi algorithm by using the self-built indoor digital maps to dynamically calculate possible paths was proposed. The Viterbi algorithm could improve the error correction capability and could effectively eliminate interferences caused by wrong paths. This navigation method could effectively avoid wrong paths through the wall appearing. Compared with the conventional inertial navigation system, the accuracy of the walk in correct rooms in complex indoor environments increased by 23%.

inertial navigation system; Viterbi algorithm; magnetic digital map

2096-2835(2016)04-0429-06

10.3969/j.issn.2096-2835.2016.04.013

2016-09-27 《中国计量大学学报》网址：zgjl.cbpt.cnki.net

TN96

A