硫酸合水纳米颗粒在湍射流中演化过程的B-TEMOM模拟

岳 言，苏中地

(中国计量大学 计量测试工程学院，浙江 杭州 310018)

硫酸合水纳米颗粒在湍射流中演化过程的B-TEMOM模拟

岳 言，苏中地

(中国计量大学 计量测试工程学院，浙江 杭州 310018)

利用双峰泰勒展开矩方法结合大涡模拟方法,研究在湍射流情况下硫酸合水纳米颗粒的形成以及随后的成核、凝并、凝结等生长情况.包含了水蒸气和硫酸分子的不可压缩气体射入含有背景气溶胶颗粒物的稳定流体域形成纳米颗粒，对颗粒的尺寸分布、质量浓度以及背景颗粒与生成颗粒之间的竞争关系进行了研究.结果表明，大涡拟序结构会增强颗粒在流动中的扩散运动，造成了不同峰之间颗粒的转移.在背景颗粒浓度为5×1011、直径为100 nm时，背景颗粒物对新颗粒的抑制作用最为显著.

泰勒展开矩方法；大涡模拟；颗粒物成核与凝并

气相化学反应系统在生产高纯度颗粒物中的使用非常常见，Pratsinis[1]，Jeong和Choi[2-3]通过研究火焰燃烧法制备二氧化硅和二氧化钛颗粒，发现这些过程可以被描述为双峰直径分布模式.Jung等[4]研究了水滴除尘的过程,Lee和Wu[5]等研究了水蒸气去除气溶胶颗粒的过程，Jonasz和Fournier[6]的研究结果发现通过引入较大颗粒来控制重金属污染物的排放是一种很有前景的方法.同时这些人的研究结果都表明，上述过程的颗粒尺寸分布实际上都满足双峰的尺寸分布模式.

双峰模型是描述颗粒尺寸的一种方法，该模型将颗粒尺寸分为两个区间，其中较小峰内的颗粒在布朗运动的作用下，会发生碰撞进而形成较大的颗粒，同时小颗粒还会附着在大颗粒的表面形成体积更大的颗粒，当颗粒体积增长到一定程度后会转移到另一个峰内.在不同的区间上将颗粒通用动力学方程转化成矩方程，通过求解不同区间上的前三阶矩，可以获得颗粒的关键信息，比如颗粒数浓度、颗粒质量浓度、颗粒平均直径、颗粒的多分散性等[7-10].

自从Yu等[8]于2008年.提出了泰勒展开矩方法(TEMOM)，该方法被不断的证明是一种高效可靠的求解复杂气溶胶颗粒相关问题的方法.而传统的求解颗粒通用动力学方程(PGDE)的方法，如矩方法，包括对数正态矩方法、积分矩方法、直接积分矩方法，分区方法和蒙特卡洛法，在求解单峰问题的气溶胶颗粒问题上都有很好的表现，但是这些方法在求解双峰问题的时候，都有各种不完善的地方.本文采用了Yu和Chan[7]于2015年提出的新型的求解复杂气溶胶颗粒问题的双峰TEMOM(B-TEMOM)方法.此方法的数学形式简单，可以非常容易地与CFD软件耦合.这里采用B-TEMOM方法与Fluent耦合的方式，研究了在固定背景颗粒物情况下的新生成颗粒的瞬态结果和稳态结果.

1 研究方法

大涡模拟的基本思想是将流动看为两个部分[11]，其一是受流动影响较大的大尺度涡结构，其二是由各向同性的小尺度结构.将不可压缩流动控制方程采用大涡模拟分解后，从N-S方程中可以得到动量方程和连续性方程：

(1)

(2)

其中，ui是滤波后的速度,v是流体的动力学粘度,ρ是被看作不可压缩流体的气体密度(该参数可以被看作是常数)，i,j分别是x，y方向；Tij表示的是亚格子尺度模型的网格应力张量，关于亚格子尺度模型的构建如下：

(3)

其中，vt是亚格子尺度的粘度，Tkk是各向同性的亚格子尺度的应力张量，sij是滤波速率的应变张量.基于Smoluchowski平均场理论，Yu和Lin[8]提出了关于尺度为v和v＇的表示颗粒数随时间演化的方程，该方程是关于颗粒数n的方程，将该变量转化成矩变量后，方程如下：

(4)

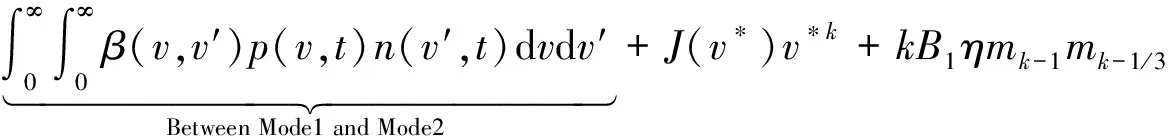
(5)

这里n(v,t)dv代表的是Mode1中的颗粒数密度，p(v,t)则表示的是Mode2中的颗粒数密度,β(v,v)是不同尺寸的颗粒的碰撞频率.方程(5)中J表示的是均相成何速率；v*是Mode2中的临界成核分子簇体积；B1是硫酸水蒸气的凝结系数，是关于温度T的函数；η则是无量纲的硫酸分子浓度；变量α为水蒸气的影响系数.在方程(4)中，第三项和第四项分别为颗粒在不同峰之间的转移而导致的颗粒数密度的增加和减小项.同样的，方程(5)的第三项和第四项也是颗粒数密度的增加项和减小项，这里的颗粒数的变化是由于颗粒在不同峰之内的转移，以及新颗粒的生成和峰内颗粒的碰撞造成颗粒凝并的共同作用导致的.其中，表征颗粒凝并作用的碰撞频率β(v,v)在连续区的表达式如下：

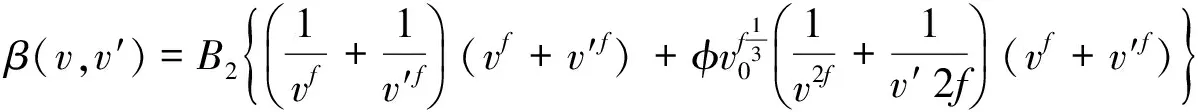
(6)

其中，B2=2kBT/3μ，kB是玻尔兹曼常数，μ是载体气体的动力粘度，f=1/Df，Df则代表颗粒分型数，λ则是空气分子的平均自由程.颗粒初始直径在本文中为定值0.4 nm.

一般的，泰勒展开矩方法只需要取前三阶矩就可以获得比较精确的结果，方程(4,5)中的令k等于0,1,2，就可以取得矩方程的前三阶矩，分别代表颗粒数密度、颗粒质量浓度、颗粒的多分散性.当k取值0,1,2时，方程(4,5)中会产生分数阶的矩，此时需要引入泰勒级数展开技术，将分数阶矩转化为关于前三阶矩的多项式：

(7)

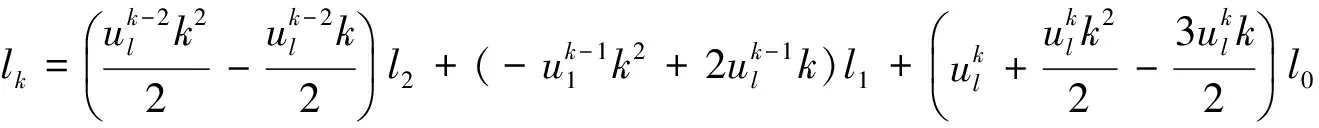
(8)

其中，um和ul为不同模式的泰勒级数展开点，在Mode1中，um=m1/m0，在Mode2中，ul=l1/l0，在本文中，采用了与Pratsinis等[1]相同的方法将矩方程进行了无量纲处理：

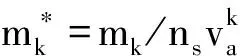
(9)

计算区域是一个二维平面射流，如图1，x方向和y方向，分别为流动方向和横向方向，流体域尺寸为20W×40W.喷射入口直径为5mm，硫酸和相对湿度为95%的水蒸气以6m/s的速度射入含有背景颗粒物的稳态区域，射流气体温度400K.入口边界条件为速度入口,出口设置outflow，压力速度耦合采用QUICK方法，湍流模型选用可以捕捉到流动细节的LES模型，入口雷诺数Re约等于2 000.流体域网格使用结构化网格，在入口处以及中轴线部分进行了加密集处理，网格总数20.8万，经过网格无关性实验，该网格数目和边界条件可以保证流场计算的准确性.

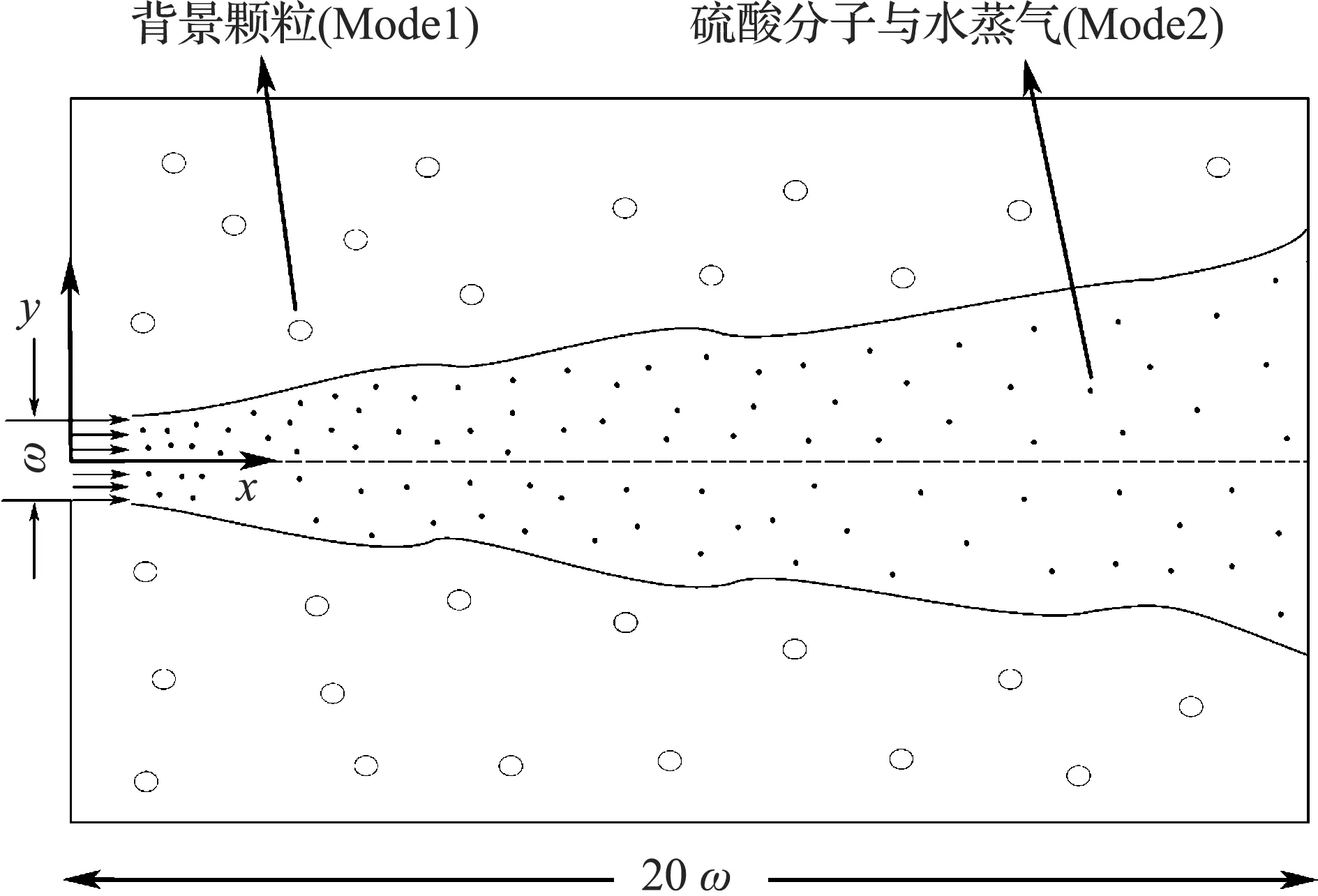
图1 流体区域设置Figure 1 Planar jet flow configuration

2 结果与讨论

2.1 流场

根据Forstall和Shapiro[12]的实验，射流速度的沿径向的分布应该满足高斯正态分布，速度的截面分布应该满足方程：

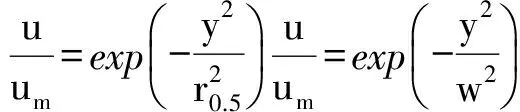
(10)

这里u是流场中横截面上的流向速度，um是流场中轴线处的流向速度，w是流场宽度的一半.根据实验结果，横截面上的流向速度分布在x=6.8 ω处之后应该满足自相似分布.在本文中，流场的数值模拟的结果如图2，当x>6.8 ω时，流向速度分布开始符合高斯正态分布，这说明平面射流的数值模拟结果接近实验与理论结果，计算结果是可靠的.

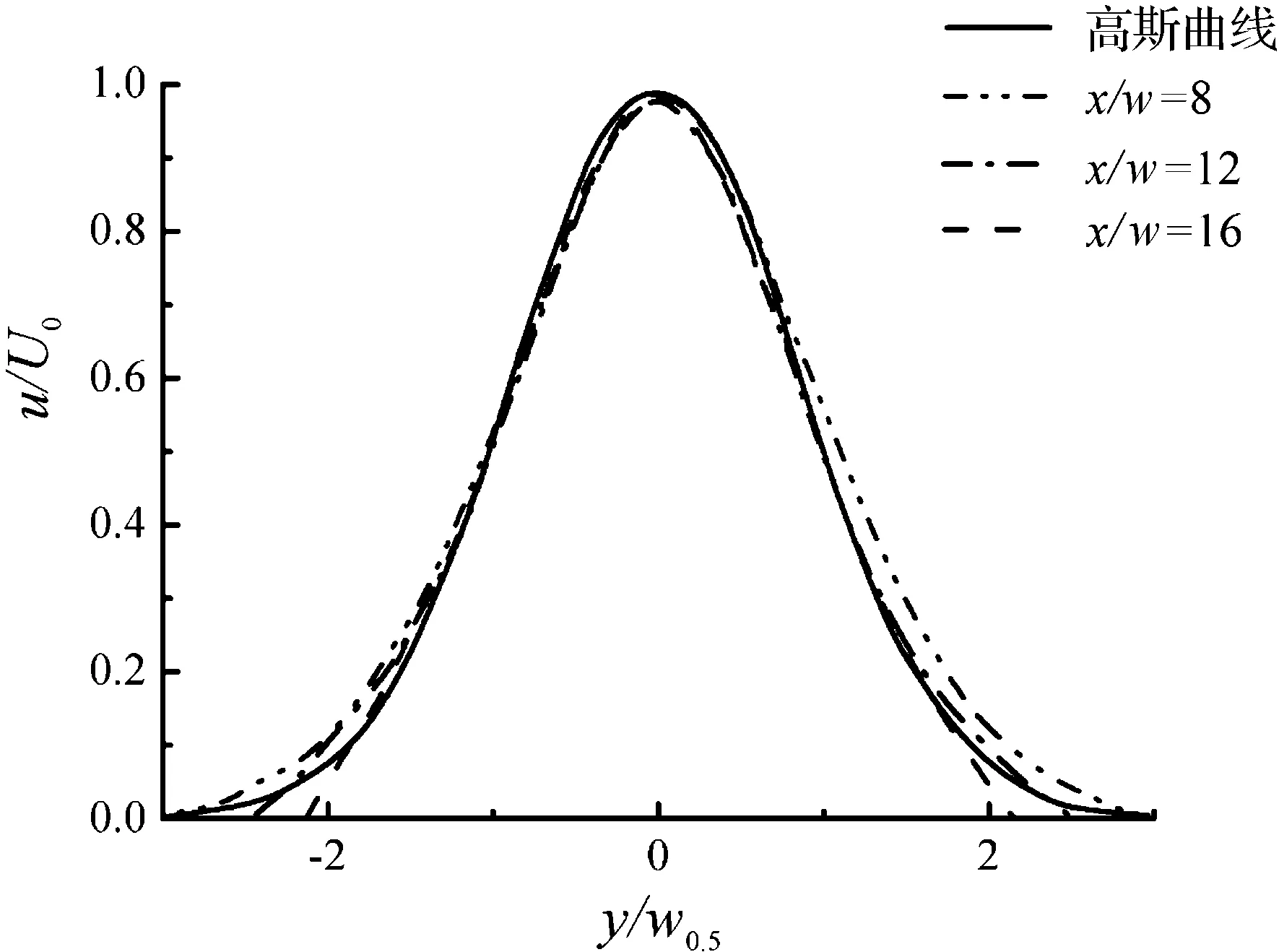
图2 不同位置下的轴向速度分布Figure 2 Jet centerline velocity profiles at different y positions

2.2 颗粒场

在湍流流场中，大涡拟序结构演化过程包含了颗粒的随空间和时间的演变过程.对于纳米颗粒两相流系统，关注的重点一般在颗粒数密度、颗粒质量浓度、颗粒的多分散性以及颗粒的平均直径.在对这些关键物理量进行瞬态分析时，重点关注颗粒动力学特性急剧变化的近喷口区域.图3和图4显示了不同无量纲时间T时的颗粒数浓度M0和L0，分别为背景颗粒物浓度和气相生成的二元成核颗粒物.

如图4，在射流气体与环境气体的混合区域，颗粒数浓度L0相对喷口内部较高.这表明，硫酸和水的二元均相成核只发生在载体气体与环境气体交界处.在射流的下游区域，载体气体与环境气体的强烈混合加剧了颗粒的扩散效应，表现为颗粒数浓度的急剧下降.但是，下游中轴线附近的颗粒数浓度有所增加，这归因于两个方面：其一是交界面处生成的颗粒由于大涡逆序结构的卷吸用，导致外围部分的颗粒进入中心区域；另一方面由于下游不同气体的混合，中心区域也有新的颗粒生成.这两点就造成了下游中心区域颗粒数浓度的增大.尽管如此，在下游区域，交界面处的的颗粒数浓度依然大于中轴线附近的颗粒数浓度，这可以说明交界面处的颗粒生成速率远高于下游大涡中心区域.

颗粒形成的唯一原因是由于二元晶质成核的存在.在射流充分发展的下游区域，成核、凝结和凝并共同作用导致的颗粒尺寸大小的变化.图5显示颗粒平均直径dlp的瞬时分布，可以看出平均颗粒的分布与颗粒数浓度L0相似；同样的，颗粒平均直径的分布也会受到大涡逆序结构的影响.射流中心区域的颗粒尺寸在射流喷口区域接近于0，结合图4可知该区域几乎没有新的颗粒产生，在下游区域的中轴线附近，颗粒平均直径开始逐渐增大，然而载体气体与背景气体的交界处的颗粒平均直径还是远大于大涡内部区域.这是由于交界处有极大的成核率以及流动特性的急剧变化都增强了颗粒间的碰撞次数，造成了外部颗粒的颗粒成长较快，表现为较大的颗粒平均直径.中心区域的气体虽然在下游区域开始有颗粒开始生成以及大涡外部区域的卷吸进入内部的颗粒，但是内部颗粒会拥有较长的弛豫时间，这会使较小的颗粒有更多的机会在大颗粒(Mode1中的的颗粒)表面吸附，当颗粒直径大于4 nm后就会转移到Mode1中去.所以在Mode2中，中心区域的颗粒数一定会小于交界面处的颗粒平均直径.

图3 不同时间T的背景颗粒物浓度L0Figure 3 Particle number concentration L0 at different time T

图4 不同时间T的颗粒物浓度M0Figure 4 Particle number concentration M0 at different time T

图5 不同时间T时颗粒的直径分布Figure 5 Instantaneous contour of particle mean diameter at different time

2.3 时间平均分析

为了研究不同背景颗粒物对于新生成的颗粒的影响，按照表2中的五种工况作了数值模拟，研究了不同背景颗粒物平均直径和不同背景颗粒物浓度对新生成的颗粒物的影响.图6显示了新生成的颗粒物的浓度与平均直径沿y方向的分布曲线.颗粒的扩散作用稀释了颗粒数浓度如图6.从图6(a)，6(b)可以看出，可以看到不同的背景颗粒物浓度和颗粒物平均直径，都会对新生成的造成影响，其中较大的背景颗粒物直径会抑制交界面处的新生成的颗粒的浓度.同样，较大的背景颗粒浓度会明显的抑制新生成的颗粒物浓度.但从图6(c)，6(d)中，似乎不同的背景颗粒物浓度和背景颗粒物直径对新生成颗粒的平均直径没有显著的影响，这主要是由于模型的局限性，图6所显示的只是新生成的颗粒物的信息，当颗粒尺寸超过一定值时，就会转移到背景颗粒物中去了，这一过程称为颗粒物的在不同模式之间的转移，所以图6(c)，6(d)中的结果显示为径向的颗粒直径分布趋于平缓，且数值上不超过3 nm.

表1 不同背景颗粒物下的工况Table 1 Simulation parameters of studied cases in time-averaged analysis

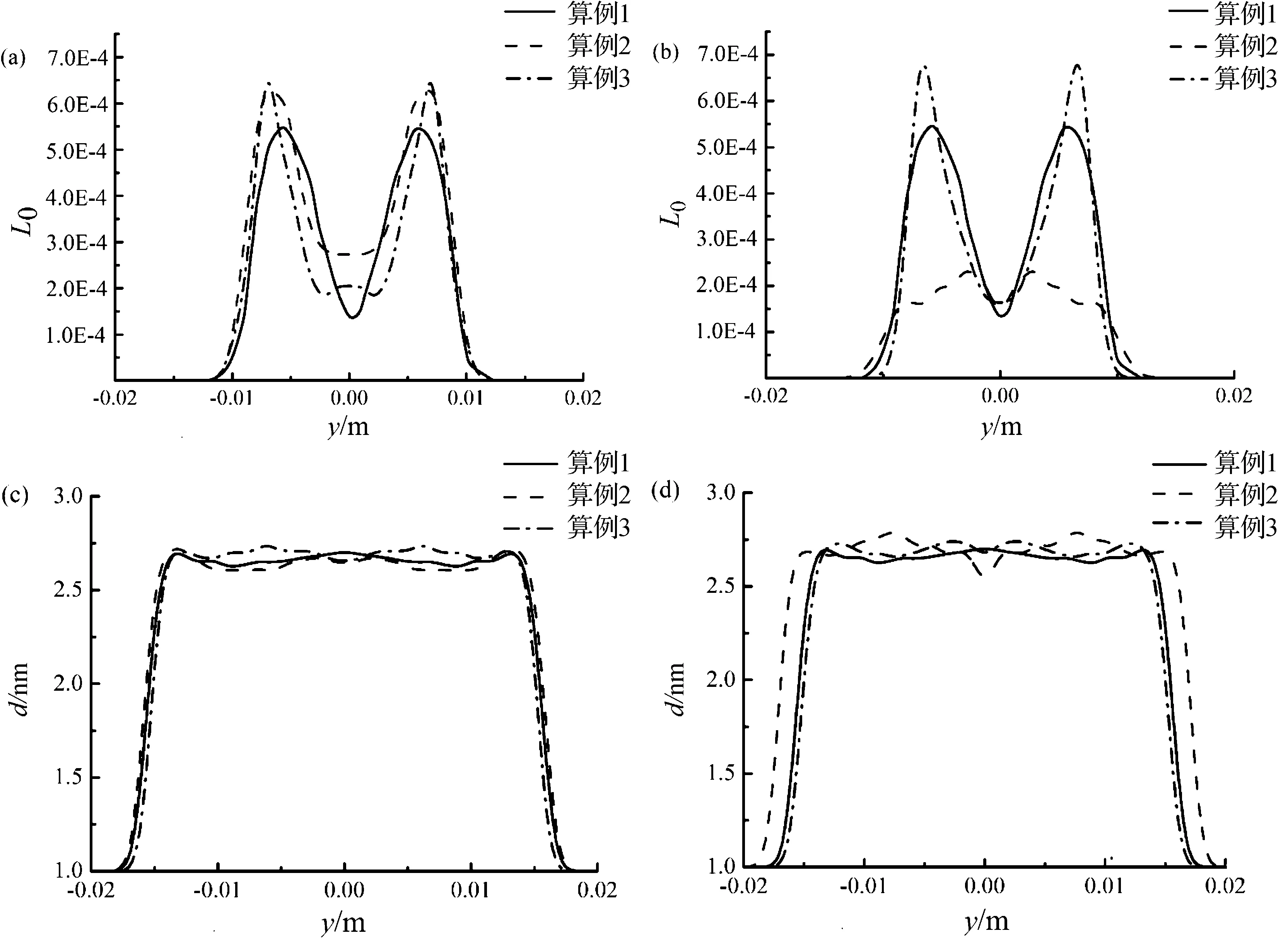
图6 不同背景颗粒物工况下颗粒物浓度L0和dlpFigure 6 Cross-stream profiles of the particle number concentration L0 and dlp at different condition

3 结 语

采用双峰矩方法研究了平面射流情况下的颗粒的成核、成长、凝并和凝结.湍流模型使用了LES方法，流场中设置为特定物理参数的背景颗粒物场，研究了瞬态情况下的模拟结果.通过求解矩方程,得到了颗粒物随时间演化的瞬时结果，瞬态结果显示颗粒数浓度，颗粒的平均直径的分布情况与流动的大涡逆序结构相似，说明颗粒的尺寸分布会受到流动影响.同时，在时间平均分析中可以看到，背景颗粒物对新生成的颗粒物会有一定的抑制作用，提高背景颗粒数浓度有利于抑制新生成的颗粒物的浓度，同时改变背景颗粒物的粒径也可以达到吸附小颗粒的目的.

[1] PRATSINIS S E. Simultaneous Nucleation, Condensation, and Coagulation in Aerosol Reactors[J]. Journal of Colloid Interface Science,1998,124(2):416-427.

[2] JEONG J I, CHOI M. A bimodal particle dynamics model considering coagulation, coalescence and surface growth, and its application to the growth of titania aggregates[J]. Journal of Colloid Interface Science,2005,281(2):351-359.

[3] JEONG J I, CHOI M. A bimodal moment model for the simulation of particle growth[J]. Journal of Aerosol Science,2004,35(9):1071-1099.

[4] JUNG C H, KIM Y P, LEE K W. A moment model for simulating raindrop scavenging of aerosols[J]. Journal of Aerosol Science,2003,34(9):1217-1233.

[5] LEE S R, WU C. Size distribution evolution of fine aerosols due to intercoagulation with coarse aerosols[J]. Aerosol Science and Technology,2005,39(4):358-370.

[6] JONASZ M, FOURNIER G. Approximation of the size distribution of marine particles by a sum of log-normal functions[J]. Limnology and Oceanography,1996,41(4):744-754.

[7] YU M Z, CHAN T L. A bimodal moment method model for submicron fractal-like agglomerates undergoing Brownian coagulation[J]. Journal of Aerosol Science,2015,88:19-34.

[8] YU M, LIN J Z. Taylor-expansion moment method for agglomerate coagulation due to Brownian motion in the entire size regime[J]. Jounarl of Aerosol Science,2009,40(6):549-562.

[9] YU M, LIN J Z. Solution of the agglomerate Brownian coagulation using Taylor-expansion moment method[J]. Journal of Colloid Interface Science,2009,336(1):142-149.

[10] YU M, LIN J Z, Chan T L. A new moment method for solving the coagulation equation for particles in brownian motion[J]. Aerosol Science and Technology,2008,42(9):705-713.

[11] 刘慧洁,于明州,尹招琴，等.柴油发动机尾气纳米颗粒演变的Temom-Les模型[J].科技导报,2015,33(6):64-68. LIU H J,YU M Z, Yin Z Q. Evolution of nano-particles within a diesel car exhaust plume via TEMOM-LES method[J]. Science & Technology Review,2015,33 (6):64-68.

[12] FORSTALL W, SHAPIRO A H. Momentum and mass transfer in coaxial gas jets[J]. American Society of Mechanical Engineers-Transactions-Journal of Applied Mechanics,1951,19(2):219-220.

B-TEMOM simulation of the sulfuric and water nanoparticles evolution in turbulent flows

YUE Yan, SU Zhongdi

(College of Metrology and Measurement Engineering, China Jiliang University, Hangzhou 310018, China)

The processes of formation, nucleation, coagulation and condensation of sulfuric-water vapor nanoparticles in turbulent flows were simulated by using bimodal Taylor-series expansion method of moments (B-TEMOM) combined with large eddy simulation (LES). When an incompressible gas containing sulfuric and water vapor was injected into a stationary flow field with background aerosols, the spatial and temporal particle size distribution (PSD), the particle number, the mass concentrations, and the competition between the formation of initial and background particles in turbulent flows were studied. The instantaneous results show that the large coherent structure strongly affects the distribution of particle number and mass concentrations, and particle polydispersity. When the background particle concentration and mean diameter equal to 5×1011and 100nm, the background particles inhibit significantly the formation of new particles.

bimodal Taylor-series expansion method of moments (B-TEMOM); large eddy simulation; nanoparticle formation and growth

2096-2835(2016)04-0382-07

10.3969/j.issn.2096-2835.2016.04.005

2016-10-18 《中国计量大学学报》网址：zgjl.cbpt.cnki.net

X169

A