基于二元语义Archimedean S-模集成算子的群决策方法

王中兴，陈 晶，兰继斌

(广西大学数学与信息科学学院，广西 南宁 530004)



基于二元语义Archimedean S-模集成算子的群决策方法

王中兴，陈 晶，兰继斌

(广西大学数学与信息科学学院，广西 南宁 530004)

对于二元语义环境下的多指标群决策问题，本文采用扩展Archimedean S-模定义二元语义的新运算法则，并基于新运算法则给出对权重进行自适应调整的二元语义扩展Archimedean S-模集成(TASTA)算子、二元语义扩展Archimedean S-模加权平均(TASTWA)算子和二元语义向量扩展Archimedean S-模加权平均(V-TASTWA)算子。以及提出一种基于TASTWA算子和V-TASTWA算子的群决策方法，并通过实例说明决策方法的可行性与有效性。

二元语义；群决策；Archimedean S-模

1 引言

由于客观事物的复杂性、不确定性以及人们思维的模糊性，决策者通常采用语言形式(如“好”、“一般”、“差”等语言术语)对事物进行定性的描述。虽然语言术语形式的评价贴近实际，但在实际应用中有时出现语言术语失真等问题。为克服语言术语在实际应用中存在的不足，Herrera[1-2]提出了采用二元组的形式即二元语义表达决策者的评价，因而二元语义在群决策中的应用受到了国内外学者广泛关注[3-13]。

目前，基于二元语义的群决策方法的研究主要集中在以下两个方面：一方面是研究二元语义的集成算子[2,4-7]。Herrera和Martinez[2]提出二元语义有序加权平均(T-OWA)算子。姜艳萍和樊治平[4]将模糊集成算子中的有序加权几何(OWG)算子扩展到二元语义有序加权几何(T-OWG)算子，并进一步分析了TOWA算子和T-OWG算子所具有的性质。魏峰等[5]结合T-WA算子和T-OWA算子提出二元语义混合加权平均(T-HWA)算子，以及给出一种基于T-HWA算子的语言群决策方法。张尧和樊治平[6]针对指标值和权重值均为语言评价信息的群决策问题，提出拓展语言有序加权平均(ELOWA)算子，并应用到多指标决策问题中。刘兮等[7]针对具有语言评价信息的多属性决策问题，提出了二元语义广义有序加权平均(T-GOWA)算子和二元语义诱导有序加权几何(T-IOWG)算子。另一方面则是研究指标或专家权重的确定方法[8-13]。徐天应和干晓蓉[9]基于粗糙集理论处理离散语言信息，提出粗糙集信息熵法确定指标权重的方法，并应用在二元语义多指标群决策中。王晓等[10]针对属性权重信息未知的情形建立基于离差最大化的目标规划模型，得到求解属性权重公式。周宇峰和魏法杰[11]建立先验权重评价指标体系和后验权重的度量准则，针对专家评价信息为模糊判断矩阵时的情形给出计算后验权重的方法。张异和魏法杰[12]考虑了语言评价过程中修饰语言的重要性，以及不同专家的犹豫程度对其权重的影响，提出一种组合赋权的方法来确定专家权重。

值得指出的是，Herrera等[2,4-7]定义的二元语义运算法则在实际应用中存在越界现象。为此，本文基于扩展Archimedean S-模定义二元语义的新运算法则，有效地避免二元语义在运算时所出现越界的问题。以及考虑专家评价与群体评价的一致性，对专家权重进行自适应调整，给出二元语义TASTA算子、TASTWA算子和V-TASTWA算子，进而提出一种基于TASTWA算子和V-TASTWA算子的二元语义群决策方法。最后通过数值实例验证方法的可行性与有效性。

2 预备知识

2.1 Archimedean S-模

定义2.1[14-15]二元函数S:[0,1]×[0,1]→[0,1]被称为S-模，若S满足下面条件：

1)(交换律)S(x,y)=S(y,x),∀x,y∈[0,1]；

2)(结合律)S(x,S(y,z))=S(S(x,y),z),∀x,y, z∈[0,1]；

3)(单调性) 若x≤x′,y≤y′，则S(x,y)≤ S(x′,y′)；

4)(边界条件)S(0,x)=x,∀x∈[0,1]。

定义2.2[14-15](Archimedean条件) 若S-模对任意的x∈(0,1)，都有S(x,x)>x成立，则称此S-模为Archimedean S-模。

定义2.3[16]称二元函数S:[0,τ]×[0,τ]→[0,τ]

(τ>0)为扩展S-模，若S满足下面条件：

1)(交换律)S(x,y)=S(y,x),∀x,y∈[0,τ]；

2)(结合律)S(x,S(y,z))=S(S(x,y),z),∀x,y, z∈[0,τ]；

3)(单调性) 若x≤x′,y≤y′，则S(x,y)≤ S(x′,y′)；

4)(边界条件)S(0,x)=x,∀x∈[0,τ]。

类似的，若扩展S-模对任意的x∈(0,τ)，都有S(x,x)>x成立，则称此扩展S-模为扩展Archime-dean S-模。

Lan Jibin等[16]指出对任意的扩展Archimedean S-模可表示为：

Sφ(x,y)=φ-1(φ(x)+φ(y))。

(1)

其中φ(t)为一元连续且严格单调递增的函数，满足条件φ(0)=0,φ(τ)=+。例如，取，则。

2.2 二元语义

二元语义是指采用一个二元组(li,αi)形式来表达专家的评价信息。其中li∈L为语言术语；αi∈[-0.5,0.5)为符号转移值，表示语言术语的集成结果与L集中最贴近的语言术语li的偏差。

定义2.4[1]设语言术语li∈L，则通过函数ϑ:L→L×[-0.5,0.5)可将li转换为相应的二元语义，即ϑ(li)=(li,0)。

定义2.5[1]设β∈[0,τ]为与语言术语经集成后相对应的实数，则β可通过函数Δ:[0,τ)→

L×[-0.5,0.5)转换为相应的二元语义，即Δ(β)=(li,αi)。其中：

(2)

以上“round”为四舍五入取整函数。

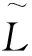
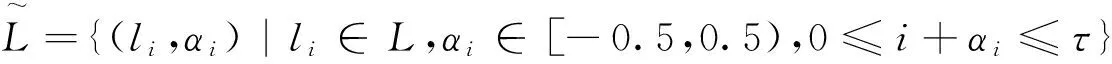
1)若i>j，则(li,αi)≻(lj,αj)；

2)若i=j，则

①当αi>αj时，则(li,αi)≻(lj,αj)；

②当αi=αj时，则(li,αi)=(lj,αj)；

③当αi<αj时，则(li,αi)(lj,αj)。

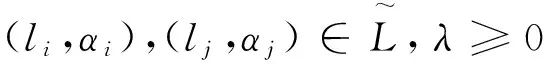
1)(li,αi)⊕(lj,αj)=Δ(Δ-1(li,αi)+Δ-1(lj,αj))；

2)λ⊗(li,αi)=Δ(λ(Δ-1(li,αi)))。

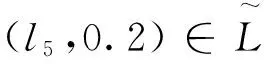
为了克服二元语义运算法则所存在的上述缺陷，下文将基于扩展Archimedean S-模，给出一种二元语义的新运算法则。

3 基于扩展Archimedean S-模的二元语义决策方法

3.1 二元语义新运算法则

1)(li,αi)⊕(lj,αj)=Δ(φ-1(φ(Δ-1(li,αi))+φ(Δ-1(lj,αj))))；

2)λ⊗(li,αi)=Δ(φ-1(λφ(Δ-1(li,αi))))。

其中φ(t)为一元连续且严格单调递增的函数，满足条件φ(0)=0,φ(τ)=+。

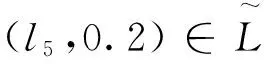
新运算法则具有下列性质。

1)(交换律)(li,αi)⊕(lj,αj)=(lj,αj)⊕(li,αi)；

2)(结合律)((li,αi)⊕(lj,αj))⊕(lk,αk)=(li,αi)⊕((lj,αj)⊕(lk,αk))；

3)(数乘分配律)λ((li,αi)⊕(lj,αj))=λ(li,αi)⊕λ(lj,αj)；

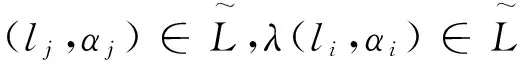
证明1)由定义3.1有：

(li,αi)⊕(lj,αj)=Δ(φ-1(φ(Δ-1(li,αi))+φ(Δ-1(lj,αj))))=(lj,αj)⊕(li,αi)。

2)((li,αi)⊕(lj,αj))⊕(lk,αk)=Δ(φ-1(φ(Δ-1(li,αi))+φ(Δ-1(lj,αj))))⊕(lk,αk)=Δ(φ-1(φ(Δ-1(li,αi))+φ(Δ-1(lj,αj))+φ(Δ-1(lk,αk)))=(li,αi)⊕((lj,αj)⊕(lk,αk))。

3)λ((li,αi)⊕(lj,αj))=λΔ(φ-1(φ(Δ-1(li,αi))+φ(Δ-1(lj,αj))))=Δ(φ-1(λφ(Δ-1(li,αi))+λφ(Δ-1(lj,αj))))=λ(li,αi)⊕λ(lj,αj)。

β=φ-1(φ(Δ-1(li,αi))+φ(Δ-1(lj,αj)))∈[0,τ]。

从而由定义3.1、定义2.5有：

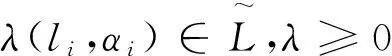
3.2 二元语义集成算子

在实际的群决策问题中，由于专家的专业水平、工作经验和综合能力等不同，各专家对评价对象给出的评价往往存在着差异性。因此，为了提高决策的准确性，需要对专家权重进行适当的调整，即对那些与群体评价差异较大或者一致度较低的专家应赋予较小的权重。反之，对与群体评价差异较小或一致度较高的专家应赋予较大的权重。基于此思想，本文以专家评价与群体评价的一致度对专家的权重进行自适应调整，并提出以下几种集成算子。

(3)

p((lθ(k),αθ(k)))=1-

(k=1,2,…,h)

(4)

在下文的定义中，均设φ(t)为一元连续且严格单调递增的函数，满足条件φ(0)=0,φ(τ)=+。

(5)

考虑到被集成的评价具有不同的权重，下面对TASTA算子进行推广。

(6)

1)(置换不变性) 设(lη(k),αη(k))(k=1,2,…,h)是(lθ(k),αθ(k))(k=1,2,…,h)的一组重排二元语义序列，则

TASTA((lθ(1),αθ(1)),…,(lθ(h),αθ(h)))=TASTA((lη(1),αη(1)),…,(lη(h),αη(h)))

(7)

TASTWA((lθ(1),αθ(1)),…,(lθ(h),αθ(h)))=TASTWA((lη(1),αη(1)),…,(lη(h),αη(h)))

(8)

2)(幂等性) 设(lθ(k),αθ(k))=(lθ,αθ)(k=1,2,…, h)，则：

TASTA((lθ(1),αθ(1)),…,(lθ(h),αθ(h)))=(lθ,αθ)

(9)

TASTWA((lθ(1),αθ(1)),…,(lθ(h),αθ(h)))=(lθ,αθ)

(10)

(lθ-,αθ-)≤TASTA((lθ(1),αθ(1)),…,(lθ(h),αθ(h)))≤(lθ+,αθ+)

(11)

(lθ-,αθ-)≤TASTWA((lθ(1),αθ(1)),…,(lθ(h),αθ(h)))≤(lθ+,αθ+)

(12)

3.3 TASTWA算子的推广

为适用于多维二元语义信息的集成，下面将TASTWA进行推广。首先定义二元语义向量的运算法则。

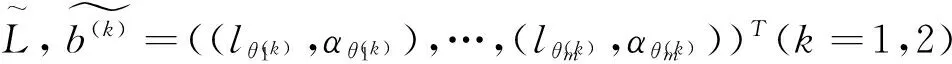
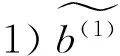
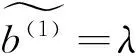
(13)

(14)

(15)

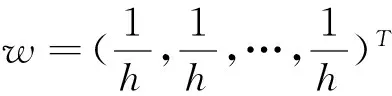
在实际的多指标群决策问题中，TASTA算子、TASTWA算子和V-TASTWA算子通过一致度确定或修正专家的权重与加权平均集成形成群体评价，以提高决策的准确性。

4 基于新集成算子的群决策方法

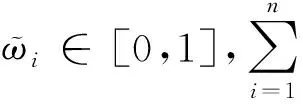
步骤1 利用转换函数ϑ(li)=(li,0)，将各专家的语言评价矩阵R(k)转化为二元语义符号评价矩阵B(k)(k=1,2,…,h)。

若各专家关于各指标的权重信息完全未知，则：

其中：

步骤3 利用TASTWA算子对方案Ai关于各指标的群体二元语义评价进行集成，得到各方案Ai的综合二元语义评价值ci(i=1,2,…,m)，即：

ci=TASTWA(bi1,bi2,…,bin)

步骤4 根据定义2.7对综合二元语义评价值ci(i=1,2,…,m)进行排序，从而得到方案的排序。

5 数值实例

某企业拟从推选的4种新产品{A1,A2,A3,A4}中选出1种进行开发。为此，该企业组织4位评审专家{E1,E2,E3,E4}，从新产品竞争力(G1)、企业技术开发能力(G2)、企业组织执行能力(G3)、开发风险(G4)和开发效益(G5)等五方面逐一对4种候选产品进行评审，以便确定最佳开发的新产品。经研究专家们决定选取7标度语言评价集L={l0,l1,l2,l3,l4,l5,l6}，依据考核指标逐一对候选产品进行评价(语言评价集的具体表达视考核指标而定，如对于新产品竞争力(G1)语言评价集L={很弱，弱，稍弱，一般，稍强，强，很强})，其中，考核指标的权重向量为ϖ=(0.25,0.2,0.15,0.15,0.25)T。各专家给出的语言评价矩阵分别如下：

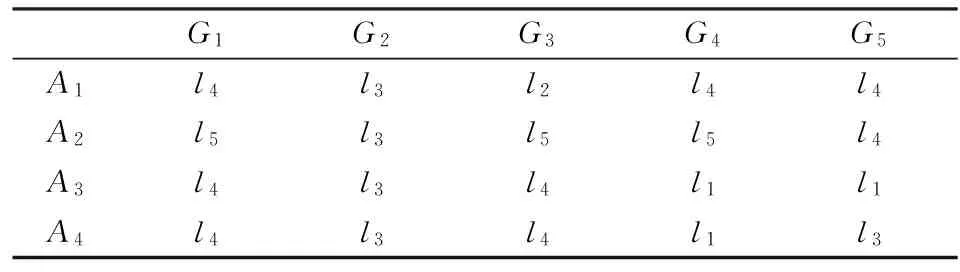
表1 专家E1给出的语言评价矩阵R(1)

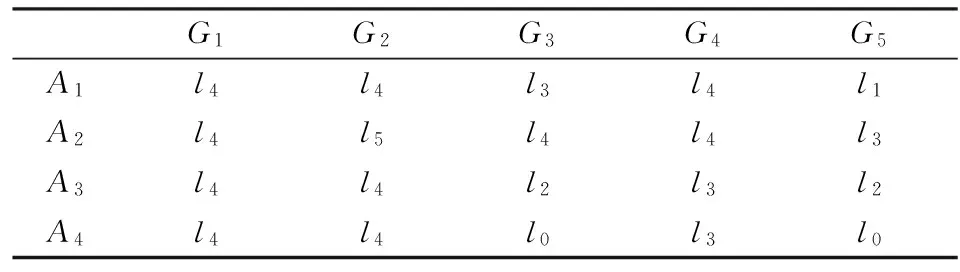
表2 专家E2给出的语言评价矩阵R(2)

表3 专家E3给出的语言评价矩阵R(3)

表4 专家E4给出的语言评价矩阵R(4)

下面釆用本文提出的决策方法进行决策。

步骤1 利用转换函数ϑ(li)=(li,0)，将语言评价矩阵R(k)转化为二元语义符号评价矩阵B(k)(k=1,2,3,4)，

B(1)=

B(2)=

B(3)=

B(4)=

步骤3 利用TASTWA算子对方案Ai(i=1,2,3,4)

各指标下的群体二元语义评价进行集成，得到方案Ai的综合二元语义评价值：

c1=(l4,-0.33),c2=(l4,-0.11)

c3=(l3,-0.05),c4=(l3,0.13)

步骤4 根据定义2.7，对综合二元语义评价值ci(i=1,2,3,4)进行排序得：c2≻c1≻c4≻c3，从而得到方案的排序A2≻A1≻A4≻A3，可见A2为最佳开发产品。

6 对比与分析

在这一小节中，将姜艳萍和樊治平等[4,6-7,13,15]中的方法与本文方法进行对比与分析，如下。

从表5可知，本文方法与已有方法明显的不同之处在于：姜艳萍和樊治平等[4,7,13,15]中决策方法需要事先给定专家的权重，才能进行决策；而在实际的

表5 不同决策方法对比

决策中，给出专家在各指标下的权重往往比较困难，本文方法则可以根据专家评价与群体评价的一致度来确定专家权重，省去了确定专家权重的复杂环节，也降低了人为因素的影响。

其次，对于专家权重确定的情形，姜艳萍和樊治平等[4,7,15]中决策方法直接集成各语言评价信息，其实质是一种主观赋权的集成方法，决策结果的主观性较大；而本文方法通过专家评价与群体评价的一致度，客观的对各专家权重进行自适应调整，能有效减少主观赋权对决策的影响。丁勇等[13]基于最小偏差法处理主客观权重的集成，与本文通过一致度调整主观权重信息均适应于群体意见分歧较大的群决策问题。

7 结语

本文基于扩展Archimedean S-模处理二元语义信息，定义二元语义的新运算法则，并提出三种二元语义集成算子，以及基于新集成算子提出一种二元语义群决策方法。新运算法则最突出特点是能避免运算法则越界，群决策方法在获得群体评价时考虑了群体评价的一致度，有利于提高决策的准确性。实例分析的结果表明该方法是可行的。

[1] Herrera F, Nartinez L. A 2-tuple fuzzy linguistic representation model for computing with words[J]. IEEE Transactions on Fuzzy Systems, 2000, 8(6): 746-752.

[2] Herrera F, Martinez L. A model based on linguistic 2-tuples for dealing with multigranulari-ty hierarchical linguistic contexts in multiexpert decision-making[J]. IEEE Transactions on Sys-tems, Man and Cybernetics Part B: Cybernetics, 2001, 31(2): 227-234.

[3] 刘德海,于倩,马晓南,等.基于最小偏差组合权重的突发事件应急能力评价模型[J]. 中国管理科学,2014,22(11):81-83.

[4] 姜艳萍,樊治平.二元语义信息集结算子的性质分析[J]. 控制与决策,2003,18(6):754-757.

[5] 魏峰,刘淳安,刘三阳.基于不确定信息处理的语言群决策方法[J]. 运筹与管理,2006,15(3):31-35.

[6] 张尧,樊治平.一种基于语言集结算子的语言多指标决策方法[J]. 系统工程,2006,24(12):98-101.

[7] 刘兮,陈华友,周礼刚.基于T-GOWA和T-IGOW A算子的二元语义多属性决策方法[J]. 统计与决策,2011,(21):22-23.

[8] 徐泽水,达庆利.多属性决策的组合赋权方法研究[J]. 中国管理科学,2002,10(2):84-87.

[9] 徐天应,干晓蓉.基于二元语义与粗糙集的多属性决策方法[J]. 统计与决策,2014,(1):27-28.

[10] 王晓,陈华友,刘兮.基于离差的区间二元语义多属性群决策方法[J]. 管理学报,2011,8(2):302-304.

[11] 周宇峰,魏法杰.一种综合评价中确定专家权重的方法[J]. 工业工程,2006,9(5):24-26.

[12] 张异,魏法杰.基于扩展的二元语义信息处理的群决策方法[J]. 中国管理科学,2011,19(S1):126-127.

[13] 丁勇,梁昌勇,朱俊红,等.群决策中基于二元语义的主客观权重集成方法[J]. 中国管理科学, 2010,18(5):165-169.

[14] Xia Meimei, Xu Zeshui, Zhu Bin. Some issues on intuitionistic fuzzy aggregation operators based on Archimedean t-conorm and t-norm[J]. Knowledge-Based Systems, 2012, 31: 78-88.

[15] Tao Zhifu, Chen Youhua, Zhou Ligang, et al. On new operational laws of 2-tuple linguistic information using Archimedean t-norm and s-norm[J]. Knowledge-Based Systems, 2014, 66: 156-165.

[16] Lan Jibin, Sun Qing, Chen Qingmei, et al. Group decision making based on induced uncertain linguistic OWA operators[J]. Decision Support Systems, 2013, 55(1): 296-303.

[17] Herrera F, Herrera-Viedma E, Verdegay J L. A model of consensus in group decision making under linguistic assessments[J]. Fuzzy Sets and Systems, 1996, 78(1): 73-87.

[18] 徐泽水.不确定多属性决策方法及应用[M]. 北京：清华大学出版社,2004.

[19] Wan Shuping. 2-Tuple linguistic hybrid arithme-tic aggregation operators and application to multiattribute group decision making[J]. Knowledge-Based Systems, 2013, 45(3): 31-40.

Method for Aggregating Two-tuple Linguistic Information Based on Archimedean S-norm and Their Application to Group Decision Making

WANG Zhong-xing，CHEN Jing，LAN Ji-bin

(College of Mathematics and Information Science, Guangxi University, Nanning, Guangxi 530004, China)

In the actual process of multi-attribute decision making (MADM), due to the complexity of objects and the inherent vagueness of human mind, the decision information is usually suitable to be expressed in natural language rather than a real number. However, natural languages always involve uncertainty and ambiguity, so it is difficult to avoid the loss of information in the process of decision making. The more the information loss, the less accurate results of decision are. In order to improve the accuracy of the decision making, it is necessary to correctly deal with linguistic decision information. And triangular norms, t-norms and s-norms and linguistic two-tuple are among the most effective ways to process linguistic information, and in this paper, based on Archimedean s-norm and linguistic two-tuple, some new operational laws of linguistic information are defined by using a continuous and strictly monotone increasing function and its inverse function. The prominent feature of such operations is that the operations are closed. Some main properties of these operations, such as commutativity, associativity and distribution law, are investigated. Moreover, considering the influence of expert weight on decision making, three new aggregation operators, including two-tuple linguistic extended Archimedean s-norm aggregation (TASTA) operator, two-tuple linguistic extended Archimedean s-norm weight averaging (TASTWA) operator and two-tuple linguistic vector extended Archimedean s-norm weight averaging (V-TASTWA) operator, are developed in this paper. All these aggregation operators use the consistency of group judgment to objectively adjust the expert weight and then effectively improve the accuracy of decision making. Later, a method for multi-attribute group decision making problems with two-tuple linguistic information is proposed based on TASTWA operator and V-TASTWA operator, and a numerical example is given to show its effectiveness and reasonability by comparison with other methods. The method not only overcomes the deficiency that the traditional operational laws of two-tuple linguistic information are not closed, but also makes full use of decision information to obtain the weight value and improves the accuracy and credibility of the results.

two-tuple linguistic information；group decision making；Archimedean s-norm

2015-03-02；

2015-07-29

国家自然科学基金资助项目(71261001)；教育部人文社会科学(12YJC630080)；广西研究生教育创新计划项目(YCSZ201451)

简介：陈晶(1990-)，男(汉族)，湖南衡阳人，广西大学数学与信息科学学院，硕士研究生，研究方向：优化与决策,E-mail: chenjing_gxu@sina.com.

C934

A

1003-207(2016)08-0146-08

10.16381/j.cnki.issn1003-207x.2016.08.018