基于方案占优和排序稳健性的多属性决策方法

2017-01-12丁涛，梁樑

中国管理科学 2016年8期

关键词：决策问题决策者赋权

丁涛，梁樑

(合肥工业大学管理学院，安徽合肥 230009)

基于方案占优和排序稳健性的多属性决策方法

丁涛，梁樑

(合肥工业大学管理学院，安徽合肥 230009)

在多属性决策问题中，不同的属性权重会产生不同的评价结果。由于实际问题的复杂性与不确定性，决策者对于属性权重的确定也存在不确定性。这些不确定既来自现实问题的复杂性和可变性，也来自决策者选择的模糊性与随机性。目前已有的研究主要是将不确定的权重信息转化为相对确定的信息(如转化为区间数等)，硬性地消除了不确定，从而给决策结果带来较大风险。本文从方案排序的视角出发，研究在权重空间下，方案的占优关系和排序的稳健性。首先，定义了占优矩阵用于刻画不确定权重信息下方案两两比较的占优关系；其次，分析了方案的排序区间，即在所有可能存在的权重组合下，方案的最好排序和最差排序。然后，定义了方案的全排序排序概率，并且给出了排序概率的计算方法。进而，我们给出了方法的决策步骤和实施过程。最后，本文将该方法应用到某远洋集团的港口评估当中。

多属性决策；占优关系；排序区间；方案排序概率

1 引言

多属性决策问题是决策者根据多个属性，对有限的方案集进行综合评价，从而进行方案优选或排序的过程。其在经济、管理和工程技术等领域都有广泛的应用[1-2]。

传统的多属性决策方法一般通过确定指标对应的属性权重，然后集成方案的综合属性值，从而进行方案的排序。近年来，研究者从不同的角度出发，提出了一系列的赋权方法，主要可以归结为主观赋权法[3]，客观赋权法[4-6]和主客观赋权法[7-10]。主观赋权法根据决策者对于不同属性的主观偏好确定权重；客观赋权法依据决策信息，利用数学规划模型，从而求解属性权重。而主客观赋权法同时结合了决策者的主观偏好和决策信息获取属性权重。

由于实际问题的复杂性和不确定性，决策者在很多情况下难以给出每个属性对应的权重值。所以，主观赋权法并不适用。而不同的客观赋权发分配权重的原则不同，因而产生的权重组合也不同。某备选方案在一组属性权重下是最优方案，其在另外一组属性权重下可能会变成较劣方案[11-12]。因此，通过赋权方法将不确定权重信息确定化会给决策带来偏差,甚至会导致决策失误的出现。

考虑到传统多属性决策方法在处理不确定权重信息下决策问题的不足，研究者提出了一系列新的多属性决策方法。Lahdelma和Salminen[13]提出了随机多指标可接受分析方法，该方法研究在权重信息完全未知时，通过确定权重分布的类型，定义了可接受度用于刻画方案排序的不确定性。Xu Zeshui等[14-17]关注于模糊多属性决策，利用模糊数、直觉模糊数和犹豫模糊数等来刻画不确定信息，在一定程度上可以用于决策分析。Wu Jie和Liang Liang[18]提出了基于DEA博弈交叉效率的多属性决策方法，该方法是将每个备选方案当做局中人，每个局中人都最大化自身的综合属性值。通过纳什讨价还价的博弈过程，进而获得最优的方案评价结果。Fu Chao和Chin[19]提出了基于鲁棒证据推理的方案比较方法，该方法通过定义在不确定权重下方案排序的鲁棒性，从而进行方案优选。 Scholten等[20]研究了不确定偏好信息下基于多属性效用理论的的复杂决策方法。该方法通过在线调查和面对面访谈分析了不确定偏好信息的来源，从而提出了基于情境分析的排序方法并对排序结果进行灵敏度分析。刘健等[21]将决策者在决策指标上存在心理阈值的现状应用到多属性决策问题当中,提出了先对决策目标调整再进行决策的方法。

上述提及的方法从不同的方面研究了不确定权重信息下的多属性决策问题，在特定的情况下具有适用性。更为一般化，本文从方案占优的视角，分析了在所有可能的权重组合(权重空间)下，方案的占优关系和排序稳健性，从而提出了一种新的方案排序方法。具体而言，我们将研究以下三个问题。在权重空间下(1).对于任意两个方案，两者的相互占优关系；(2).每个备选方案所能达到的最好排序与最差排序，即排序区间；(3).对于所有可能存在的方案排序，如何选择一种作为最终的排序结果。进而，我们提出了一种基于方案占优和排序稳健性的多属性决策实施过程。最后，我们将本文的方法应用于某远洋集团的港口评估当中，验证了其有效性与合理性。

2 问题描述

一般而言，在多属性决策问题中既存在效益型属性(越大越好)，也存在成本型属性(越小越好)。为了消除不同物理量纲对决策结果的影响，我们利用下面的公式[2]对决策矩阵进行规范化处理：

(1)

方案Xi的综合属性值为：

(2)

因此，属性权重的确定是传统多属性决策的关键问题。然而，在很多实际应用当中，属性权重是不确定的。如决策者偏好的不确定性、决策环境的可变性和不同专家难以达成一致等原因都会给确定权重带来困难。很多情况下，决策者只能给出部分权重偏好信息，甚至权重信息完全未知。此时，不同的权重确定方法会产生不同的权重组合，从而导致决策结果的不确定性。鉴于此，我们接下来将研究在不确定属性权重下，方案的占优关系和排序稳健性分析。

3 决策方法

3.1 方案成对比较

为了清晰的描述不确定权重信息，我们首先引入权重空间的概念。

定义1：设w=(w1,w2,…,wn)为一组属性权重，记Ω(w)=Ω(w1,w2,…,wn)为属性的权重空间。其中，Ω(w)为所有可能的权重组合。特别地，当权重信息完全未知时，

(3)

通常情况下，决策者可以根据其偏好，对权重进行约束。例如，对于三个属性Y1, Y2,和Y3，决策者指定：Y1的重要性至少是Y2的两倍，且Y3的重要性大于Y1，此时属性权重空间为：

(4)

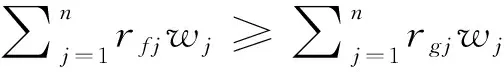
对于给定的两个方案，我们定义占优概率的概念。

定义3：对于方案f和g，其属性权重空间为Ω(w)，p(f≻g)为在属性权重空间Ω(w)下方案f优于方案g的概率，称f对g的占优概率。同样地，p(g≻f)为g对f的占优概率。其中：

p(f≻

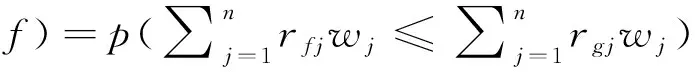
(5)

特别地，若p(f≻g)>0.5，则称方案f对g弱占优，反之亦然。

定义4：对方案集X={X1,X2,…,Xm}中的方案占优关系进行成对比较，构成方案占优矩阵P=(pij)m×m。其中，pij表示方案i对j的占优概率。

性质1：方案占优矩阵P中的元素满足：

1)pii=1，∀1≤i≤m；

2)pij+pji=1，∀1≤i,j≤m，i≠j

定义4表明，决策者可以得到两两比较的方案占优关系。显然，占优概率越大，占优关系越强。

由于权重空间的不确定性，方案占优概率无法通过模型求解，因此我们利用蒙特卡洛仿真的方法计算占优概率。在这里，我们给出一个简单的算例进行计算模拟。两个方案的属性值分别为A=(4,6,5,5) 和B=(5,4,3,6)，权重空间为Ω(w)={0≤wj≤1,j=1,2,3}。图1演示了A对B的占优频率(纵坐标)和仿真次数(横坐标)的对应关系。结果显示，仿真次数超过3500时，占优频率稳定在0.75，即p(A≻B)=0.75。

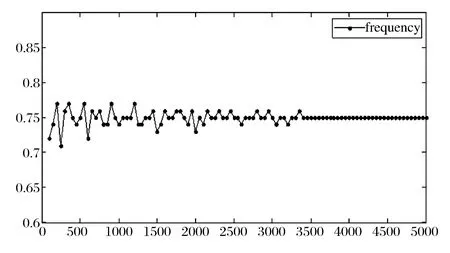
图1 A对B的占优频率模拟结果

3.2 方案排序分析

在权重空间下，对于一个给定的方案，其对应的排序位置是不确定的。即该方案在两组不同的权重组合下的排序位置可能并不相同。接下来我们给出方案排序区间的概念。

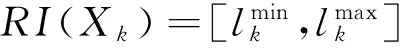
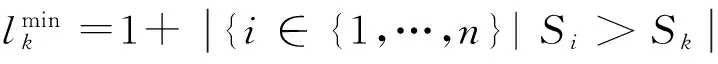
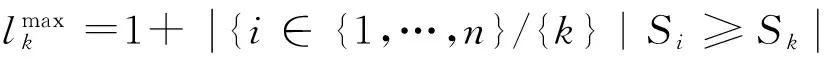
模型1：

wj∈Ω(w),

di∈{0,1}, i≠k，

其中，M为一个大于1的正常数。

模型2：

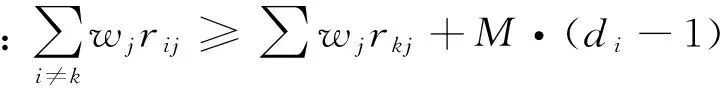
wj∈Ω(w),

di∈{0,1}, i≠k,

其中，M为一个大于1的正常数。

对于决策者而言，选择任何一种排序结果都会有忽略其它排序所带来的风险。因此，我们定义了方案排序的决策风险。

定义6：令选择方案排序Υk所带来的决策风险记为Ψ(γk) (k=1,2,…,m!)。其满足：

(1)若 p(γk)=1, 则有 Ψ(γk)=0;

(2)若 p(γk)=0, 则有 Ψ(γk)=1；

(3)对于两种方案排序 γs和 γt(s≠t),若排序概率满足：p(γs)>p(γt)，则有 Ψ(γt)>Ψ(γs)。

定义6表明排序的决策风险大小与排序概率呈负相关。鉴于此，我们认为决策者选择排序概率较大的排序结果的风险较小。

3.3 基于占优关系和排序分析的决策方法

接下来，我们给出了基于方案占优和全排序概率分析的决策方法，步骤如下：

1)形成多属性决策问题

决策者给出一个由n个属性评价m个方案的多属性决策问题，并利用公式(1)将决策矩阵标准化。

2)获得属性权重空间

决策者首先对所有属性进行综合分析，给出所有可能存在的权重组合，即权重空间，记为Ω(w)。

3)获取方案占优矩阵

通过计算方案成对比较的占优概率，从而得到方案占优矩阵P，从而得到两两比较的占优关系。

4)计算每个方案的排序区间

利用模型1和2，求解每个方案的排序区间，从而得到单个方案的排序稳健性。

5)求解方案全排序概率

首先根据步骤3)和步骤4)的结果，剔除排序概率为0(无效)的方案排序。然后，利用蒙特卡洛算法，在权重空间下计算剩下的方案排序概率。

6)最终方案排序

决策者通过设定阈值的方法，选出k(k>0)个概率较大(相对稳定)的方案排序。进而，决策者可以利用专家打分确定位置权重，利用加权平均的方法集成这些方案排序，进而得到最终的排序结果或最优方案。

接下来，我们用Wu Jie和Liang Liang[18]中的算例演示该方法的过程。对于一个由四个属性评价六个方案的多属性决策问题，原始决策矩阵为：

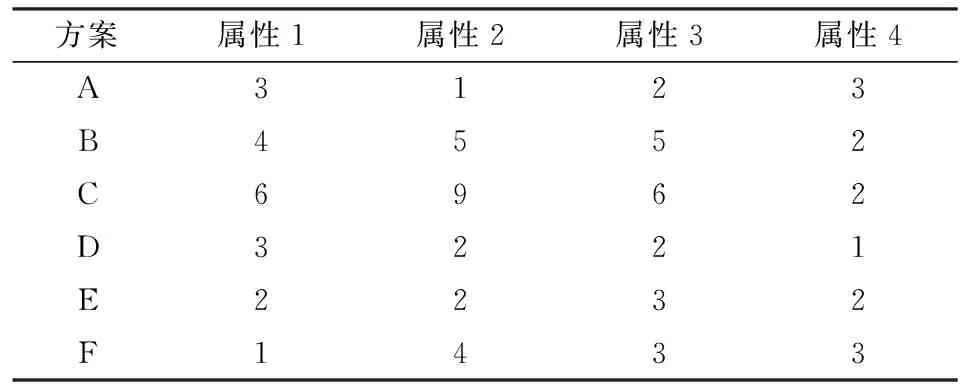
表1 原始决策矩阵

下面利用本文的方法对方案进行排序。首先利用公式(1)，对决策矩阵进行规范化处理，得到标准化决策矩阵：

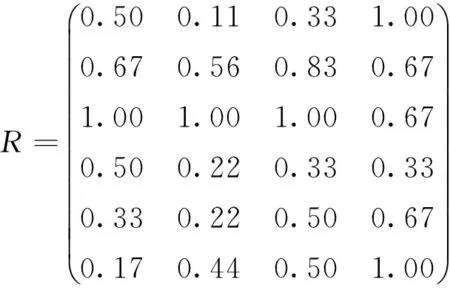
利用蒙特卡洛仿真，计算两两方案间的占优概率，得到的方案占优矩阵为：

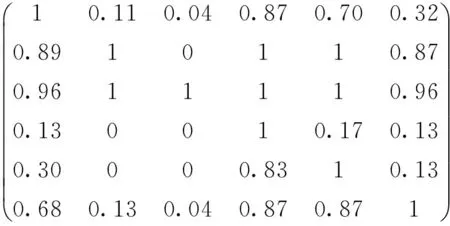
由于方案C至少弱占优于其它所有方案，方案占优的角度它是最优方案。而方案D至少被所有方案弱占优，所以它是最劣方案。

然后，根据模型1和模型2，得到所有方案的排序区间为：

RI(A)=[1,6],RI(B)=[2,4],RI(C)=[1,3],RI(D)=[3,6],RI(E)=[3,6]，RI(F)=[1,6]

从单个方案的排序区间结果可知，方案B和C的排序稳健性高于其它方案，因此相对于其它方案更优。然而，方案A,E和F的优劣难以比较。

接着，在权重空间下，对方案A,E和F进行全排序仿真，得到的全排序概率如表3所示。决策者筛选出三种较为稳健的方案排序：A>F>E，F>A>E和F>E>A。根据Lahdelma和Salminen[13],决策者给排序一到三位的位置权重分别为：1,1/2和1/3。然后，利用加权平均得到的排序为：F>A>E。

综合以上分析，最终的方案排序为：C>B>F>A>E>D。根据Wu Jie和Liang Liang[18]可知，利用自评模型得到的方案排序为：A=C=F>B>E>D;利用博弈交叉评价模型得到的方案排序为：C>A>F>B>E>D。可以看出，自评模型难以得到完整的方案排序，即方案A，C和F的优劣难以比较。而博弈交叉评价得到的最优方案和最劣方案和本文一致，但其它方案的排序结果并不完全相同。这是因为本文是从方案占优和全排序概率的视角对方案进行评价，其结果的稳健性更高。

4 案例分析

某远洋集团需要对4个港口A1,A2,A3，A4和A5进行综合评估。决策采用了多属性决策分析方法，分别从内部环境和外部环境两个方面构建指标体系。其中，内部环境指标主要包含了三个一级指标：硬件设施、内部工作效率和运营发展；外部环境指标也包含了三个一级指标刻画：政策环境、经济环境和地理环境。每个一级指标均由一些二级指标刻画。如图2所示。

表2 三个方案的全排序概率

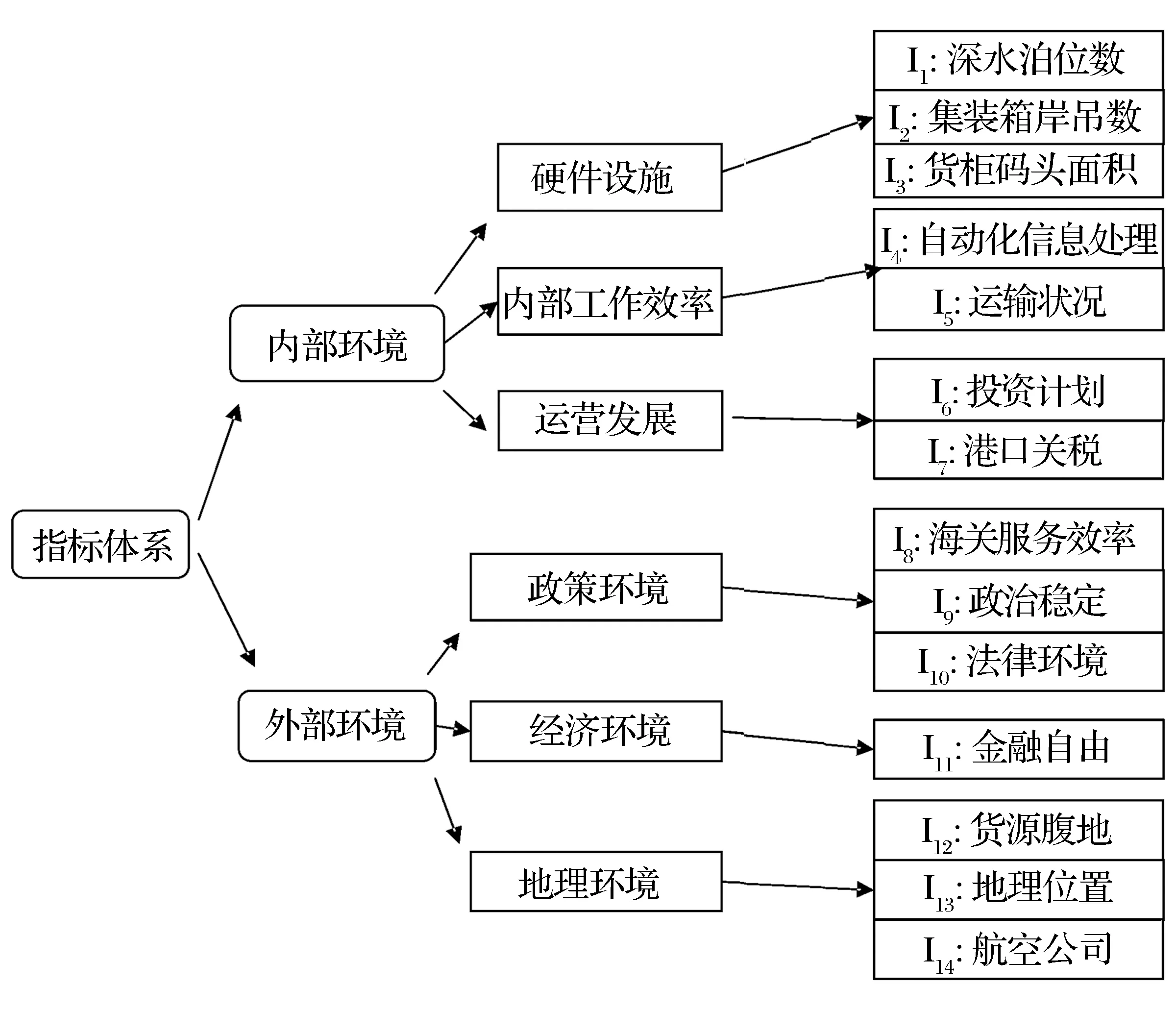
图2 港口评估的评价指标体系

为了节省空间，我们只列出了经过规范化处理之后的决策矩阵，如表3所示。

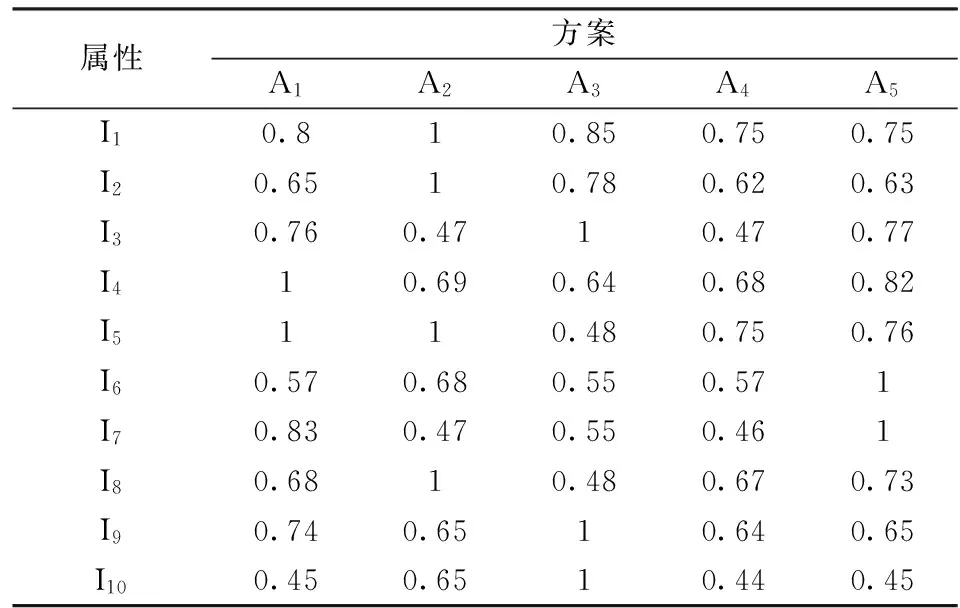
表3 标准化决策矩阵

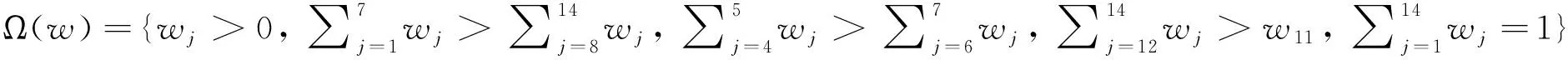
因为A5至少弱占优于其它方案，所以从方案占优的角度，它是最优方案。而A4至少被其它方案弱占优，它是最劣方案。

然后，根据模型1和2，我们计算得到每个方案的排序区间：

RI(A1)=[1,4],RI(A2)=[1,4],RI(A3)=[1,5],RI(A4)=[4,5],RI(A5)=[1,4]

从单个方案的排序区间结果可以看出A4是一个较劣方案。因为在整个权重空间下，其排序都只会在最后两位。然而，方案A1，A2和A5的优劣却难以比较。

最后，对方案A1，A2和A5进行全排序仿真，得到的全排序概率如下：

表4 三个方案的全排序概率

从表3可以看出，最大概率的方案排序为：p(A1>A2>A3)=0.810。由于该排序的概率较大，因而带来的排序风险较小，从而可以作为排序结果。

综合上述分析过程，最终的稳健性方案排序结果为：A5>A1>A2>A3>A4。

5 结语

在传统多属性决策中，属性权重的确定是研究者关注的一个焦点。然而，由于实际决策问题的复杂性与不确定性，指标权重的具体数值往往难以确定。现有的通过确定权重从而集成方案综合属性值的方法在一定程度上可以处理这种不确定性，但却无法保证排序结果的稳定性与合理性。鉴于确定权重的方法处理不确定性多属性决策问题的缺陷，本文提出了一种基于方案占优和排序稳健性的决策方法。文中给出了属性权重空间的概念，用于描述不确定权重信息。同时本文给出了属性权重空间下的方案占优概率用来比较方案的优劣。占优概率不仅能反映两个方案的优劣程度，还能刻画确定权重的方法对决策结果带来的风险系数。一方案对另一方案的占优概率越大，则认为该方案优于另一方案的参考意义更大。基于方案占优和全排序概率的思想，我们计算了(1)方案占优矩阵，用于刻画两两比较的方案占优关系；(2)单个方案的排序区间，用于描述单个方案的最好排序和最差排序和(3)方案全排序概率，用于反映方案排序的稳健性。综合分析结果，本文提出了一种新的基于方案占优和排序稳健性的多属性决策方法。

本文提出基于方案排序稳健性的全排序决策方法，避免了通过确定属性权重从而集成方案的综合属性值的思路，有效的处理了属性权重不确定的决策问题。该方法考虑到不确定权重信息给决策结果带来的风险，对于决策有指导作用。由于本文考虑的是单人决策问题，然而现实中还有一类由多个决策者共同参与的群决策问题。在未来的研究中，我们将考虑属性权重和决策者权重都未知的多属性群决策问题。

[1] Wallenius J, Dyer J S, Fishburn P C, et al. Multiple criteria decision making, multiattribute utility theory: Recent accomplishments and what lies ahead[J]. Management Science, 2008, 54(7):1336-1349.

[2] Xu Zeshui. Uncertain multiple attribute decision making: methods and applications[M]. Heidelberg, New York: Springer-Verlag, 2015.

[3] Horsky D, Rao M R. Estimation of attribute weights from preference comparisons[J]. Management Science，1984， 30(7)： 801-822.

[4] 樊治平, 张全. 多属性决策中权重确定的一种集成方法[J]. 管理科学学报, 1998, 1(3): 50-53.

[5] Shirland L E， Jesse R R， Thompson R L,et al. Determining attribute weights using mathematical programming [J]. Omega 2003，31 (6): 423-437.

[6] Wang Yingming， Luo, Ying. Integration of correlations with standard deviations for determining attribute weights in multiple attribute decision making[J]. Mathematical and Computer Modelling, 2010, 51(1-2): 1-13.

[7] 樊治平, 赵萱.多属性决策中权重确定的主客观赋权法[J] .决策与决策支持系统, 1997, 7(4):87-91.

[8] Ma Jian， Fan Zhiping, Huang Lihua.A subjective and objective integrated approach to determine attribute weights[J]. European Journal of Operational Research 1999，112 (2): 397-404.

[9] 徐泽水，达庆利. 多属性决策的组合赋权方法研究[J]. 中国管理科学. 2002, 10(2): 84-87.

[10] 王鹏飞, 李畅. 不确定多属性决策双目标组合赋权模型研究[J]. 中国管理科学, 2012, 20(4):104-108.

[11] Diakoulaki D, Mavrotas G, Papayannakis L. Determining objective weights in multiple criteria problems: the critic method[J]. Computers & Operations Research, 1995, 22(7): 763-770.

[12] 周维，王明哲. 基于前景理论的风险决策权重研究[J]. 系统工程理论与实践，2005， (2)：74-78.

[13] Lahdelma R, Salminen P. SMAA-2: Stochastic multicriteria acceptability analysis for group decision making[J]. Operational Research, 2001, 49(3): 444-45.

[14] Xu Zeshui S, Chen Jian. An interactive method for fuzzy multiple attribute group decision making[J]. Information Sciences, 2007, 177(1):248-263.

[15] Xu Zeshui, Xia Meimei, Distance and similarity measures for hesitant fuzzy sets[J]. Information Sciences, 2011， 181 (11): 2128-2138.

[16] 万树平, 董九英. 基于三角直觉模糊数Choquet积分算子的多属性决策方法[J]. 中国管理科学, 2014, 22(3):121-129.

[17] Pei Zhi. Intuitionistic fuzzy variables: Concepts and applications in decision making[J]. Expert Systems with Applications, 2015, 42(22):9033-9045.

[18] Wu Jie, Liang Liang. A multiple criteria ranking method based on game cross-evaluation approach[J]. Annals of Operations Research, 2012, 197(1):191-200.

[19] Fu Chao, Chin K S. Robust evidential reasoning approach with unknown attribute weights[J]. Knowledge-Based Systems, 2014, 59(2):9-20.

[20] Scholten L, Schuwirth N, Reichert P, et al. Tackling uncertainty in multi-criteria decision analysis-An application to water supply infrastructure planning[J]. European Journal of Operational Research, 2015, 242(1):243-260.

[21] 刘健, 刘思峰, 马义中,等. 基于心理阈值的多属性决策问题目标调整研究[J]. 中国管理科学, 2015, 23(2)：123-130.

A New Multiple Attribute Decision Making Method Based on Dominance Relation and Ranking Stability

DING Tao, LIANG Liang

(School of Management, Hefei University of Technology, Hefei 230009, China)