一类相同材料周期焊接问题的稳定性
2017-01-11罗文
罗 文
(福建商学院 基础部,福建 福州 350012)
一类相同材料周期焊接问题的稳定性
罗 文
(福建商学院 基础部,福建 福州 350012)
文章讨论了同一材料在平面弹性中的周期焊接问题,通过引入两个全纯函数,将问题转化为周期黎曼边值问题。通过应力函数的表达式,并使用柯西型积分,研究了周期焊接问题的稳定性。
应力函数;周期焊接问题;摄动;稳定性
平面弹性材料的焊接问题在工程上具有广泛的应用,以复变函数为理论工具研究平面弹性问题是个很好的方法。
1.引言
假设Γ∈C是一条简单光滑的封闭曲线,以反时针方向为正向,Γ所围成的内部区域(外部区域),记为D+(D-)。建立函数关系:
Γδ∶ξ=α(t)=t+δ(t),t∈Γ
(1.1)
当δ∈C′(Γ)时,容易得到:
(1.2)
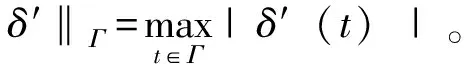
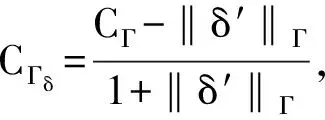
对于平面弹性基本问题[1-2],弹性体内任意点z处的应力σx,σy,τxy和位移u+iv,可以由应力函数φ(z),ψ(z)表示为:
(1.3)
其中μ,κ为弹性常数。
2.周期焊接问题
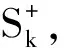
问题Ⅰ:设在一个弹性平面中有一列周期孔L0,L±1,L±2,…,以aπ为周期,在各孔上焊接材料相同的垫圈,设孔边和垫圈线间的位置差异已知,则:
(u++iv+)-(u-+iv-)=g(t),t∈L
其中g(t)也以aπ为周期,并且g′(t)∈H,在z=±∞i处的外应力为零。
3.摄动后的周期焊接问题
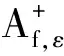
那么,称f*为f关于δ的指数为ε的n阶Sobolev型摄动,简记为Φ*∈sp(Φ,δ,ε,n)
假设焊接中问题Ⅰ的孔边和垫圈间的位置差g(t)产生误差,该误差可以看成定义3.1中的Sobolev型摄动,此时的焊接问题就是摄动后的焊接问题,即问题Ⅱ:
在一个弹性平面中有一列周期孔L0δ,L±1δ,L±2δ,…,以aπ为周期,在各孔上焊接材料相同的垫圈,该孔边和垫圈线间的位置异为:
(3.1)
其中gδ(ξ)也以aπ为周期,并且gi(ξ)∈H,i=0,1,2,在z=±∞i处的外应力为零。
根据焊接条件,问题Ⅱ的应力函数
(3.2)
(3.3)
联立(3.2)与(3.3)可以得到:
(3.4)
(3.5)
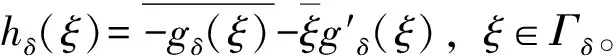
(3.6)
(3.7)
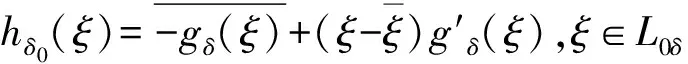
(3.6)和(3.7)是周期跳跃问题,其解分别为:
(3.8)
(3.9)
由于所讨论的焊接问题要求在Z=±∞i的外应力为零,所以可以得到焊接问题Ⅱ的应力函数为:
φδ(z)=φδ0(z),Z∈S0δ/L0δ
(3.10)
(3.11)
4.周期焊接问题的稳定性
4.1 几个引理
为了讨论应力函数的稳定性,需要以下几个引理:
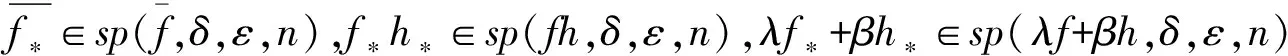
引理2:记柯西积分算子为:
与之相应的射形算子为:
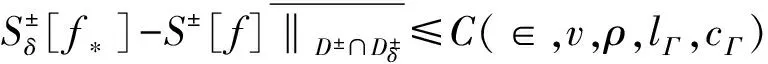
4.2 周期焊接应力的稳定性
根据(1.1)中Γδ的定义可知,如果δ≡0,t∈Γ,则Γδ=Γ,即不发生摄动,若焊接问题Ⅱ中δ=0,则可转化为焊接问题Ⅰ,因此令δ≡0,从(3.10),(3.11)可得周期焊接问题Ⅰ的应力函数为
φ(z)=φ0(z),z∈S/L
(4.1)
(4.2)
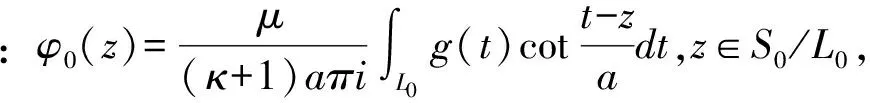
定理1 假设Γδ∈P(Γ,‖δ‖<ρ),g(i)∈sp(g(i),δ,∈,0),i=0,1那么:
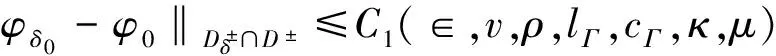
(4.3)
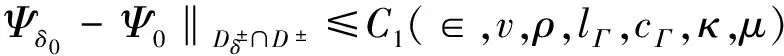
(4.4)
其中Ci(∈,v,ρ,lΓ,cΓ,κ,μ),i=1,2是不依赖于δ的常数。
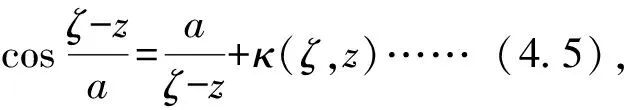
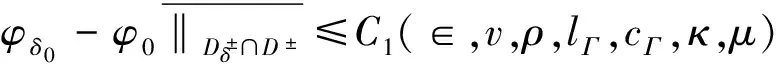
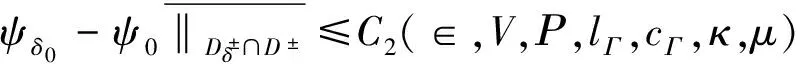
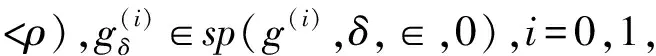
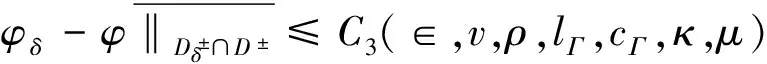
(4.6)
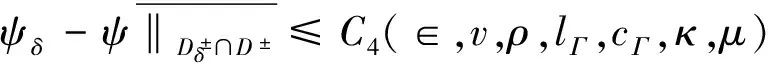
(4.7)
其中Ci(∈,v,ρ,cΓ,κ,μ),i=3,4是不依赖于δ的常数。
[1]Lu J K.Complex variable methods in plane elasticity[M].ingapore: World Scientific,1995.
[2]Muskhelishvili N I.Some basic problems of the mathematical theory of elasticity[M].Leyden:P.Noordhoff,1963.
[3]Lin Juan,Duan Ping,Xie Bihua.Stability of a kind of welding problems of infinite plane with a unit circular[J].Journal of Mathematics,2013,33(6):969-976.
[4]Juan Lin,Jinyuan Du.Stability of displacement to second fundamental problem in plane elasticity[J].Acta Mathematica Scientia,2014,34B(1):125-140.
[5]Pei Dang,Juan Lin,Jin-Yuan Du.Stability on a kind of welding problems under perturbations[J]. Applicable Analysis,2014,93(11):2478-2497.
(责任编辑:杨成平)
Stability of Periodic Welding Problem for the Same Material
LUO Wen
(Department of Foundation , Fujian Commercial College, Fuzhou 350012, China)
This paper discusses periodic welding problem for the same material in plane elasticity. By introducing two holomorphic functions, periodic Riemann boundary value is studied; by introducing stress function and Cauchy’s integral formula, the stability of the periodic welding problem is studied.
stress function; periodic welding problem; perturbation; stability
2016-11-04
罗文(1982—), 男,福建尤溪人,讲师,硕士。研究方向:基础数学。
O17
A
1008-4940(2016)06-0105-04
