基于分形方法的望江挑花图案设计研究
2017-01-11程皖豫袁惠芬刘新华
程皖豫,袁惠芬*,王 旭,2,刘新华,2
基于分形方法的望江挑花图案设计研究
程皖豫1,袁惠芬*1,王 旭1,2,刘新华1,2
(1.安徽工程大学 纺织服装学院,安徽 芜湖 241000; 2.安徽工程大学 纺织行业科技公共服务平台,安徽 芜湖 241000)
为促进分形艺术在望江挑花图案上的应用,探讨了基于L系统和矩阵Kronecker积理论的分形图形生成原理,并借助计算机图形技术进行了针对望江挑花图案的分形图案设计,最后通过手绣的方式验证了望江挑花图案的实物效果。研究表明:运用分形方法结合计算机辅助设计,通过参数调整能方便地获取多种不同效果的分形图案。为拓展望江挑花图案的主题和设计方法提供了有价值的参考。
分形;L系统;Kronecker积;望江挑花
望江挑花是安徽省纺织服装类唯一入选国家级非物质文化遗产的民间刺绣工艺。望江挑花早先作为敬神敬佛的敬褡,后逐渐以人物、动物、花卉、风景、图腾纹样、民俗题材等图案应用于家纺装饰、旅游纪念品、工艺品等[1-2]。图案设计是望江挑花制作过程的一个重要环节,长期以来挑花图案设计凭借艺人根据经验构图,创作难度大、效率低,制约了挑花工艺的发展。同时,以民俗为主的传统构图已不能满足人们对图案多样性的追求,也限制了挑花产品的应用。分形图形具有局部与整体的自相似性,在图案设计上具有重要的应用价值,并成为该领域的研究热点。分形图案的计算机生成方法有很多,其中基于矩阵Kronecker积和L系统的生成算法是比较常见的方法。文献[3]介绍了矩阵迭代变换和分形矩阵的概念,运用矩阵的Kronecker积设计出分形编织图案。文献[4]探讨了L系统的基本构成原理及其创新设计,并利用Visual Basic语言开发了绘图程序,设计出单独纹样、适合纹样、二方连续及四方连续等纺织纹样。文献[5]运用L系统的链式语言生成具有4级自相似结构的分形组织,通过填充组织的变化,配合分形组织获得一类新型的组织结构。借助电子提花技术进行织造实验为新型纺织面料的开发进行了初步尝试。文献[6]基于L系统生成具有自相似性结构的分形组织,以缎纹和缎纹变化组织为填充组织,得到具有特殊效果的分形织物组织。目前,矩阵Kronecker积和L系统在纺织领域主要集中在织物组织纹样、编织图案和提花图案设计方面,而基于分形方法的望江挑花图案设计研究尚不多见。
1 分形图形生成原理
1.1 L系统
L系统是美国生物学家Lindenmayer为模拟植物形态设计的一种形式语言。以DOL系统为例其主要思想:由a、b组成的字符串,每个字符对应一个改写规则,若a→ab,表示a用ab替换;b→a,表示b用a替换。改写过程从公理开始不断迭代[7-8]。DOL系统通常用V表示字母表,V*表示V上所有单词的集合。一个字符串OL系统是一个有序的3元素集合G=
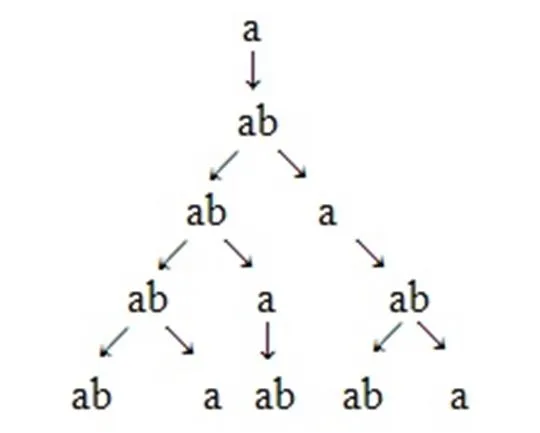
图1 L系统规则示意图
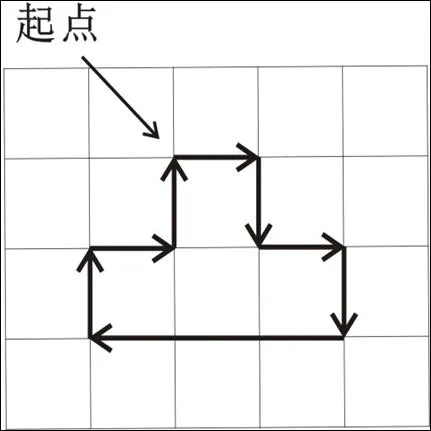
图2 L系统绘图过程示意
由Seymour Papert 开创的“龟图”系统,是用几何图形表达L系统的构图方法[9-10],例如按照G中的字符,进行如下定义:
F:向前移动一步,步长为d,画一条直线段;
E:向前移动一步,步长为d,不画;
+:向左旋转δ角;
-:向右旋转δ角。
定义小方格边长为 d,起始角度A=0°,角增量a=90°,则字符串“F-F+F-F-FFF-F-F+F”,的绘图过程,如图2所示。
1.2 矩阵的Kronecker积
令矩阵K是矩阵和的Kronecker积,若为×矩阵,而为矩阵,则K为矩阵,计算如式(1):
当布尔矩阵中,1表示黑色,0表示白色,则布尔矩阵可形成相应的图案。如图3所示,矩阵为 3×3,其图案可由图3(a)所示。当式(1)中=时,即,可得到一级分形图案,如图3(b)所示。继续迭代计算则生成具有更精细自相似结构的二级分形图案,如图3(c)所示。

(a) 矩阵A图案 (b) 一级分形图案 (c)二级分形图案
图3 基于Kronecker积的分形图案示意图
2 绘图实例
2.1 L系统绘图
根据L系统的构图原理,利用Matlab语言编写了绘图程序。设绘图起始角度为A,起始坐标为(0,0),行走步长为d,角增量a。符号集:V={F,+,-};公理w;生成规则P;循环次数为n。由表1、2、3所示,可生成分形图1、2、3分别如图4(a)、(b)、(c)。

表1 分形图1生成规则

表2 分形图2生成规则

表3 分形图3生成规则

(a)分形图1 (b)分形图2 (c)分形图3
图4 基于L系统的分形图案示意图
表1、2、3中各字符的定义符合1.1节规定。图案效果可通过调整相应的参数进行改变,如调整公理w则图案的初始状态会改变,调整初始角度则图案的起始方向会相应改变,调整生成规则P及角增量a则图案形状会改变,调整步长d和迭代次数可控制图案的大小等。
2.2 Kronecker积绘图
运用矩阵Kronecker积可形成自相似结构的分形图案,本文先对基础图案矩阵进行Kronecker积分形,再结合反组织(与基础图案矩阵元素1、0互换)与填充组织矩阵叠加,设计出适合望江挑花的图案。反组织叠加,是将基础图案矩阵A和其反组织矩阵B分别一级分形后叠加产生矩阵G,其计算如式(2)。如图5所示,图5(a)是基础组织,图5(b)是其反组织,图5(c)、(d)分别是基础组织和反组织矩阵的一次分形图案,图5(e)是图5(c)、(d)叠加的形成的图案。

(a)基础组织A(b)反组织B(c)A一级分形(d)B一级分形(e)叠加效果
填充组织叠加,是将基础组织A和其反组织B的矩阵一级分形后,再计算B与填充组织矩阵C的Kronecker积,最后叠加得到矩阵G,其计算如式(3)。如图6所示,图6(a)是基础组织图,图6(b)是其反组织图,图6(c)是填充组织图,图6(d)是叠加后的图案。
图5和图6说明运用矩阵Kronecker积可获得分形效果的图案,如改变基础组织A其反组织B也会产生变化,或者改变填充组织C,并相互叠加,即获得多种不同效果的分形图案,可提高图案的设计效率。

(a)基础组织A (b)反组织B (c)叠加组织C (d)叠加效果
图6 填充组织叠加示意图
3 分形艺术图案在望江挑花上的应用实例
由L系统产生的分形图案,可根据公理、初始角度、角度增量、生成规则的灵活运用设计出望江挑花的主体图案,其效果适合运用游针表现手法[11]。如图4中的图案(a),完整匀称,轮廓精美,似一朵旋转的四瓣花,给人以律动的感觉。选用25×25cm的棉质底布进行图案的挑花绣织,实物效果如图7(a)所示。由矩阵Kronecker积方式绘出的图案严谨端庄,块面感强,适合运用十字针表现手法[11]。如图5(e)是反组织叠加法得到的图案,结构细腻,适用于望江挑花的边饰或主体图案。选用20×20cm的棉质底布进行图案的挑花绣织,实物效果如图7(b)所示。图6(d)是填充组织叠加法得到的具有回纹效果的图案,较适合作为望江挑花的局部边饰。选用25×25cm的棉质底布进行挑花绣织,实物效果如图7(c)所示。上述两种分形图案产生方法通过改变相应参数,可产生风格多变的挑花图案。

(a)实例1(b)实例2(c)实例3
[1] 高山,王世福.望江挑花艺术产品的设计与开发[J].艺术探索,2011,25(3):107-108.111.
[2] 朱胜甲.望江挑花及其艺术特征[J].安庆师范学院学报(社会科学版),2010,29(5):122-124.
[3] 王小铭,李福清.基于分形矩阵的编织图案设计与生成[J].纺织学报,2003,24(4):37-39.
[4] 孟广利,杨旭红.L系统分形图在纺织纹样设计上的应用[D].苏州:苏州大学,2012.
[5] 李琴,岑科军.基于L系统的印花图案设计[J].丝绸,2008,45(7):12-13.
[6] 贾静静,张聿.基于L系统的缎纹分形组织及其织纹效果设计[J].丝绸,2011,48(5):32-34.
[7] 齐东旭.分形及其计算机生成[M].北京:科学出版社,1994.
[8] 邱玮炜,安宁,戚烜.基于MATLAB的Koch分形图生成算法研究[J].计算机与数字工程,2010,38(8):99-101.
[9] 张聿,金耀,孙家武.基于L系统的织物分形组织设计方法[J].纺织学报,2007,28(5):51-54.
[10]帅昌浩,李勇.基于分形理论的图形设计研究与应用[D].西安:西安科技大学,2008.
[11]袁惠芬,方妍,王旭,等.望江挑花针法形成规律研究[J].武汉纺织大学学报,2016,29(2):29-32.
Investigation on Wangjiang Cross Stitch Pattern Design by Fractal Method
CHENG Wan-yu1, YUAN Hui-fen1, WANG Xu1,2, LIU Xin-hua1,2
(1. College of Textile and Clothing, Anhui Polytechnic University, Wuhu Anhui 241000, China;2. The Science and Technology Public Service Platform for Textile industry, Anhui Polytechnic University, Wuhu Anhui 241000, China)
In order to promote the fractal art in the application of Wangjiang cross stitch pattern, the L system and the matrix Kronecker product pattern generated principles and fractal pattern design for Wangjiang cross stitch based on computer graphics technology were discussed. The graphics effects of Wangjiang cross stitch were validated by hand embroidered experiments. The result shows various fractal patterns can be easily generated by changing the parameters of fractal with the help of computer aided design and fractal method. This study provides valuable reference for expanding theme and design method of Wangjiang cross stitch.
Fractal; L system; Kronecker product; Wangjiang Cross Stitch
TS101.8
A
2095-414X(2016)06-0053-04
袁惠芬(1972-),女,教授,研究方向:服装数字化技术.
纺织面料安徽省高校重点实验室开放基金(2015FZ001);安徽工程大学国家自然基金预研项目(2016).
