基于粗糙集聚类的商品房市场经济区划研究

李祎琛，杨 琳

(武汉大学 土木建筑工程学院，湖北 武汉 430072)

基于粗糙集聚类的商品房市场经济区划研究

李祎琛，杨 琳

(武汉大学 土木建筑工程学院，湖北 武汉 430072)

针对我国目前商品房市场存在的问题，基于系统聚类分析的方法从不同区域商品房价格轨迹的特点，判断我国35个大中城市现有商品房市场经济区划及投资潜力，根据各层次分级特点构建了跨区域分散-组合投资策略，并利用粗糙集模型对指标体系进行了优化约简。系统聚类分析的结果表明，我国商品房市场具有明显的层次性，其经济区划可分为内部同质、彼此异质的4个层次，依次为商品房市场发达区、较发达区、较落后区及落后区，并且城市化率、房地产开发投资、人均GDP等指标对城市房地产分类具有显著影响，是判断商品房市场投资潜力的主要影响因素。

经济区划；分散-组合投资；粗糙集理论；系统聚类分析

一直以来，商品房市场价格的布局及其合理性都受到人们广泛关注。研究表明，依据价格走势对主要城市商品房市场进行划类并进行分散-组合投资，克服了单纯按照地理位置或者行政级别进行市场分组的盲目性，不仅有助于降低投资者的风险、针对性地制定宏观调控政策，还有利于整个国家商品房市场的稳定和协调发展[1-2]。国外对于商品房市场空间结构分布特征的研究较早，主要集中于商品房投资与区位的研究，并侧重于从城市经济学与区位角度系统研究商品房产业发展[3]。反观我国，相关研究起步较晚，主要从城市宏观和微观区位两个层次研究区位对商品房市场的影响[4]。虽然国内外对商品房投资与经济增长的关系都进行了大量研究[5-6]，并形成相对成熟的研究理论体系，但是较少涉及区域经济对商品房市场的作用。尽管国内相关专家学者对商品房投资与区域经济增长关系进行了一定研究，叶贵等[7]运用灰色关联法对房地产区域市场投资竞争潜力进行评价，发现区域经济发展潜力与房地产投资竞争潜力之间存在相关关系；此外还有学者对房地产投资与国民经济包容性增长、房价波动与区域经济增长之间的关系进行了研究[8-10]。但相关研究仍处于初步探索阶段，对商品房市场与区域经济协调发展的内部机制研究深度不足。并且，有关我国商品房市场空间分布特征或区域差异性的研究大多停留在对商品房市场现状的描述，并没有深入地研究其内部形成机制与作用机理。

笔者拟通过粗糙集和系统聚类分析对我国35个大中城市商品房市场进行经济区划，以探索不同地区商品房市场价格运动轨迹的相似性和差异性，并将聚类结果与规范的计量经济学模型相结合，以期帮助开发者合理预期商品房市场，做出理性的分散-组合投资决策。

1 理论模型构建

1.1 指标体系的建立

系统聚类分析的指标体系要选取能够代表区域商品房市场实际情况的经济变量。笔者参考相关城市竞争力评价、宜居城市评价及“中国房地产TOP10研究组”相关指标体系，选择代表市场有效需求和潜在需求的指标作为评价指标体系[11]。根据科学性、可行性原则，并考虑数据的可得性，具体指标如表1所示。

1.2 模型建立

1.2.1 连续属性离散化

粗糙集是一种刻画不完整性和不确定性的数学工具，可以对数据进行分析和推理，从中发现隐

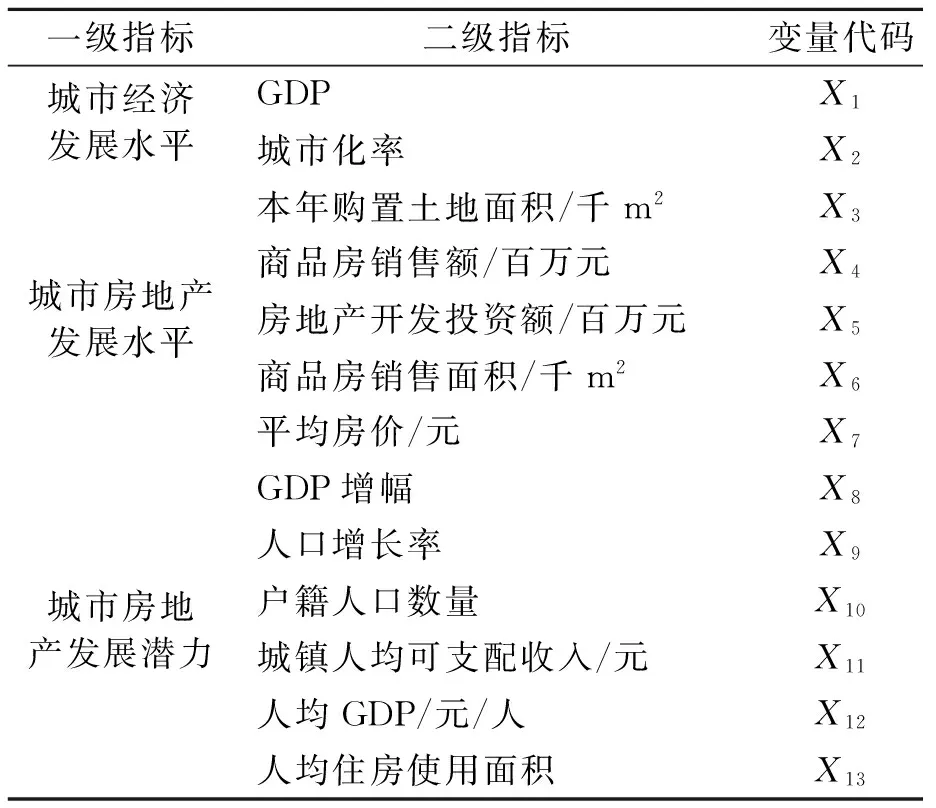
表1 投资潜力评价指标体系

含的知识，揭示潜在的规律，其处理对象是离散化的值或属性。因此，连续属性的离散化是粗糙集计算的基础，其根本目的是在保证预测系统信息有效性的前提下，对预测系统进行约简，将属性空间或值域空间划分为尽可能少的子空间，以消除指标因素之间的共线性，提高预测指标的有效性。笔者选取等距离散化的方法，将每组属性值进行等距离划分，具体步骤如下：①划分每组属性值的取值范围，确定最大值xmax和最小值xmin；②设定划分区间的数目n，此处取n=3；③计算区间步长d=(xmax-xmin)/n；④计算区间划分点的值，即c0=xmin，c1=c0+d，c2=c0+2d，…，cn=xmax。

1.2.2 指标优化约简

影响商品房市场的指标体系是一个复杂的系统，冗余的指标信息输入不仅加重了聚类模型的负担，而且降低模型的泛化能力。笔者引入粗糙集理论对复杂的指标体系进行约简，在不需要先验知识的情况下删除一些无用的因素，实现了对聚类模型输入变量的优化。基于粗糙集理论聚类指标的优化约简及其权重的确定可分为以下几个步骤：

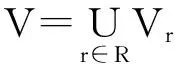
(2)计算决策表中条件属性等价类关系集合ind(B)(B⊆X)。等价关系ind(B)构成了U的一个划分，用U/ind(B)={A1,A2,…,An}表示，其中Ai表示不同的等价类，在ind(B)下与X不可分的所有对象构成一个等价类,记为[A]ind(B)。

(3)根据步骤(2)中求出的等价类关系集合，计算其重要程度。在信息系统S=(U,X,V,f)中，a∈A的重要性可定义为：

SX(x)=|H(X)-H(X-x)|

(1)

式中：H(X)表示所有属性组成集合X的信息熵；H(X-x)表示集合X除去属性x的信息熵。SX(x)越大表明该属性的重要程度越高。

定义一个属性子集B⊆X的信息熵H(B)为：

(2)

(4)计算评价指标权重Wi及偏离程度Di。其中Di是该评价指标与最大权重指标的偏离程度。根据偏离程度对冗余指标进行约简，一般来说当指标偏离程度大于90%时，该指标被约简。

1.2.3 系统聚类模型

聚类分析可以对各个城市的商品房市场进行经济区划。聚类是研究分类问题的一种多元统计方法。所谓类是指相似元素的集合。系统聚类分析的基本思想为：设集合G中有n个样本X1,X2,…，Xn，首先每个样本独自成为一类，计算类内样本的距离，将距离最近的两个类聚为一类。然后计算新类间的距离，并将最近的两个类聚为一类。以此循环，直到所有的类聚为一类。笔者选用离差平均和系统聚类法，具体步骤如下：

(1)选择分析变量，每个样本独自成类，生成变量矩阵：

X=(xij)

i=1,2,…,n；j=1,2,…，p

(3)

其中，n、p分别为样本数和变量数。

(2)选择距离或相似系数的计算公式，生成距离矩阵或相似矩阵作为系统聚类统计量，距离主要用于样品分类，相似系数主要用于变量的分类。笔者是对样品进行分类，所以选择欧氏距离平方作为聚类统计量，该矩阵元素的计算方法为:

(4)

(3)选择聚类方法，将距离最近的两个样本合成一类。笔者选取离差平方和法(ward法)进行聚类。

(5)

(6)

(7)

定义D(G1,G2)=D12-D1-D2,事实上，若G1,G2内部点与点距离很小，则其能很好地各自聚成一类，并且这两类又能够充分分离(即G12很大)，这时必然有D=D12-D1-D2很大。因此，按定义可以认为G1,G2之间的距离很大。

(4)重复上述步骤，直到所有样本归为一类。

(5)输出聚类结果和系统聚类图，并根据实际情况及分类准则等得出最终经济区划。

2 模型估计与计量结果分析

2.1 聚类因子优化分析

2.1.1 粗糙集分级

对原始数据进行n=3的等距离离散化后得到信息表，如表2所示。表2中以2014年35个大中城市为研究对象，每个研究对象有13个属性。

2.1.2 聚类指标的优化

(1)构建聚类因子信息系统S=(U,X1,V,f)。其中，属性X1={x1,x2}；U={a1，a2，…,a16}。

表2 离散化信息表

(2)对于聚类因子所对应的属性集X1={x1,x2}。运用Matlab7.0计算可得：

(3)计算聚类因子指标的重要程度。根据式(2)分别求得H(X1)=1.898 3，H(X1-x1)=0.676 2，H(X1-x2)=0.664 7。根据式(1)可以确定聚类因子指标属性的重要程度：

在粗糙集优化预测因子指标时，若约简指标过多，信息量丢失严重，则达不到全面决策的精度；若约简指标过少，则达不到剔除无用信息的要求。根据目前的研究经验和实践，一般约简指标比例应控制在20%～30%之间为宜，因此笔者设置约简阈值为90%，即当Di>90%时，此指标被约简。同理求得表2中所有预测因子的重要度SA、权重偏离程度Di，计算结果如表3所示。

表3 指标信息量表

①根据权重偏离程度Di>90%的筛选原则对指标因子进行约简，由表3的计算结果可知：商品房销售额、商品房销售面积、平均房价、GDP增幅、户籍人口数量、人均住房使用面积等指标的权重偏离程度大于90%，此类指标对整个聚类模型的影响度较小；②城市化率、房地产开发投资额、人均GDP等指标对于聚类模型的影响较大，这类指标代表了区域城市的发达程度，反映了城市居民住房购买力和商品房市场的增长潜力、发展空间。

2.2 系统聚类模型分析

笔者对系统聚类模型进行计量回归分析。根据系统聚类分析提出的合理分组数，利用系统聚类分析的重复迭代算法实现组内欧几里聚类最小，按照类间差异大、类内差异小的分类原则确定每组的成员，把不同商品房市场分成内部同质、彼此异质的经济区划，确定我国35个大中城市商品房市场的经济区划，如表4所示。

表4 系统聚类分析经济区划

基于系统聚类分析结果，从表4可知：①各组规模差异大，例如第1组中仅包含北京、上海、广州、深圳4个商品房市场，而第4组中则包兰州、长春、南宁等11个商品房市场；②同组内的商品房市场大部分同属于一个地区或者同处于一个经济发展水平上，第3、4组中的商品房市场大部分来自于发展中的二线城市，而其他组城市的经济发展水平相对更高，也具备更加成熟的商品房市场。结合各个聚集区指标值，对35个大中城市商品房市场作如下划分：

(1)商品房市场发达区：北京、上海、广州、深圳。京沪广深地区作为我国的政治经济文化中心，在吸引人才、技术、资本等方面具有独特的优势，其产业经济基础雄厚，对商品房市场发展具有强大的人口和经济支撑，市场供需比较平衡。而且受益于良好的经济政策环境、强大的科技经济实力及消费阶层人口的扩张，京沪广深地区商品房市场能够保证稳定的吸纳量和容量空间，市场将进一步成熟完善，具有很大的投资价值。但政府在商品房市场的发展中也要进行合理的引导与调控，保证商品房市场产业结构均衡，投资进度平稳，以防投资过热而引起房地产市场泡沫。

(2)商品房市场较发达区：重庆、天津、杭州、厦门、南京、成都、武汉、大连、沈阳。此类城市多为区域经济增长中心，人口较多，且经济实力强。虽然短期内此类城市与京沪广深相比，商品房市场发展程度还有不小差距，但是随着产业转移、基础配套设施完善及就业岗位的增加，城市经济将步入快速发展阶段，良好的城市发展空间将激化商品房市场的发展，投资、居住需求都将逐步释放，商品房市场开发潜力巨大。政府也应该提供良好的政策红利，拉动城市的投资效应，促进商品房市场进一步发展。

(3)商品房市场较落后区：西安、昆明、郑州、南昌、哈尔滨、合肥、长沙、青岛、济南、宁波、福州。此类城市大多属于我国中西部地区的二三线城市，经济基础较为薄弱，商品房市场表现相对惨淡，发展较为滞后。但是商品房的供需比较均衡，市场发展较为健康。随着产业结构升级、基础设施完善等因素的刺激，这类城市商品房市场将得到稳步发展，市场环境将进一步改善，可作为投资者选择性进入的城市。政府部门也要采取利好的政策措施，为商品房市场发展提供良好的经济基础、产业环境、政策环境。

(4)商品房市场落后区：兰州、长春、南宁、呼和浩特、贵阳、石家庄、西宁、海口、太原、乌鲁木齐、银川。这些城市大多分布在我国的中西部地区，受制于当地经济基础薄弱的现状，商品房市场发展不完善。而且大多城市还存在人口外流的现象，有限的消费能力与政府粗放式的商品房市场开发形成鲜明对比，造成商品房市场定位失准、业态同质化，短期内使得商品房市场供求结构矛盾突出，投资潜力较低。政府部门理应做好商品房市场开发规划，积极引进资金、技术和人才，发展当地产业经济，促进商品房市场良好运行发展。

3 结论

笔者首先运用粗糙集理论对指标体系进行优化约简，然后采用系统聚类分析方法对全国35个大中型城市商品房市场进行经济区划，并研究目前中国商品房市场跨区域分散-组合投资的经济基础。①利用粗糙集理论对评价指标体系进行优化约简，可以有效地筛选指标因子，剔除信息量小的指标因子，降低了模型的噪声，提高了评价模型的精度；②聚类分析的结果表明，目前中国大中型城市的商品房市场主要分成4类：由于特殊的政策支持和独特的资源环境，北京、上海、广州和深圳的商品房市场供求表现有别于其他城市整体状况，特别是北京商品房市场在全国房地产市场中表现最为特别，没有其他城市与其类似；部分内陆城市或者经济欠发达地区的商品房市场与沿海城市差别较大，但绝大多数城市房地产市场的表现存在共性，这主要是因为这些城市商品房市场的投资环境变化节奏一致，房地产市场周期基本相同。因此，可以考虑选择在不同组别之间选择合适的城市分散-组合房地产投资；③粗糙集分析结果肯定了经济基础的存在，认为城市商品房市场的表现与自身的经济基础条件相匹配也证明了聚类分析的正确性。城市化率、房地产开发投资额、人均GDP对城市房地产分类具有显著影响，是判断商品房市场投资潜力的主要影响因素，投资者应对各城市商品房市场投资潜力进行理性判断，充分考虑自身经济实力，做出有关分散-组合投资的合理决策。

[1] 贾生华,任超群,仇丽.房地产企业跨区域投资的城市选择方法[J].中国房地产，2010(11):63-37.

[2] 张坤,曾爱花.中国房地产区域投资组合实证研究[J].经济评论,2009(2):31-36.

[3] CHENG P, ROULAC S E. Measuring the effectiveness of geographical diversification[J]. Journal of Real Estate Portfolio Management, 2007,13(1)：113-123.

[4] 朱京曼,石先进.宏观经济波动与房地产市场的动态关系：基于脉冲响应分析的实证研究[J].首都经济贸易大学学报,2014,16(2):14-20.

[5] 程鸿群,邹敏,张洛熙,等.湖北省房地产投资环境的时序全局主成分分析[J].武汉理工大学学报(信息与管理工程版),2015,37(4):447-451.

[6] EMAMIZADEH B, HANAI M A. Rearrangements in real estate investments[J]. Numerical Functional Analysis and Optimization,2009,30(5-6):478-485.

[7] 叶贵,汪红霞.房地产区域市场投资竞争潜力的灰色关联评价[J]. 经济问题, 2009(10):41-44.

[8] 陆菊春,贾自武,田洪芬.房地产投资对经济增长效应及区域性差异的研究[J].武汉理工大学学报(信息与管理工程版),2008,30(6):959-963.

[9] 黄忠华,吴次芳,杜雪君.房地产投资与经济增长：全国及区域层面的面板数据分析[J]. 财贸经济,2008(8):56-60.

[10] 王利蕊.中国房地产投资对国民经济包容性增长的实证研究[J].经济问题,2013(8):48-53.

[11] 倪鹏飞,赵璧,魏劭琨.城市竞争力的指数构建与因素分析：基于全球500典型城市样本[J].城市发展研究,2013,20(6):72-79.

LI Yichen:Postgraduate; School of Civil Engineering and Architecture, Wuhan University,Wuhan 430072, China.

Research on Economic Regionalization of Real Estate Markets Based on Rough Set Clustering

LIYichen,YANGLin

According to the existing problems of the real estate market in China, this paper determines the economic regionalization and investment potential of the commercial housing market in 35 large and medium cities in China from the characteristics of the price trajectory of commercial houses in different regions based on the system cluster analysis. According to the hierarchical characteristics of each level, it constructs a cross - regional decentralized-portfolio investment strategy, and uses the rough set model to optimize the index system.The results of cluster analysis show that China′s commercial housing market has obvious hierarchy, and its economic divisions can be divided into four levels: internal homogeneity and heterogeneity,as developed area, less developed area, less developing areas and developing areas, and urbanization rate, real estate development investment and the per capita GDP has a significant influence on city real estate classification and determined the main factors that influence the investment potential of the commercial housing market.

economic regionalization; dispersion-portfolio investment; rough set theory; system cluster analysis

2095-3852(2016)06-0744-06

A

2016-06-27.

国家科技支撑计划课题基金项目(2014BAL05B00).

F293.35

10.3963/j.issn.2095-3852.2016.06.022

收稿日期：李祎琛(1993-)，女，河南平顶山人，武汉大学土木建筑学院硕士研究生.