相位共轭阵列及其形成的相位共轭声场

黎胜，李婷，刘松

1大连理工大学运载工程与力学学部船舶工程学院，辽宁大连116024

2大连理工大学工业装备结构分析国家重点实验室，辽宁大连116024

相位共轭阵列及其形成的相位共轭声场

黎胜1，2，李婷1，2，刘松1，2

1大连理工大学运载工程与力学学部船舶工程学院，辽宁大连116024

2大连理工大学工业装备结构分析国家重点实验室，辽宁大连116024

相位共轭法可实现声波反向传播和自适应聚焦，用于声源成像。从理论的角度梳理分析基于测量声压使用单极子源（PC/M）、基于测量声压梯度使用偶极子源（PC/D）、基于测量声压和质点速度使用单极子源和偶极子源（PC/P）这3种相位共轭阵列及其形成的相位共轭声场之间的关系，以及PC/P相位共轭声场与源声场的关系。从倏逝波和传播波角度给出上述3种阵列能否突破衍射极限的理论依据，并基于线列阵进行数值仿真，给出阵与源的距离、阵元间距、阵元偏移对各阵聚焦的影响。结果表明：当阵长一定时，在近距离处PC/D聚焦效果最佳；在阵与源距离较远处，以半波长阵元间距的PC/M聚焦效果最佳。

相位共轭阵列；相位共轭声场；倏逝波；聚焦特性

0 引 言

舰船噪声越来越受到重视：提高舰艇声隐身性能已成为世界海军力量综合发展的一个重要方向；MSC.338（91）通过的SOLAS公约II-1章3-12条修正案要求强制实施新的船上噪声水平规则；国际海事组织海洋环境保护委员会也开始使用非强制性的“减少商船水下辐射噪声导则”，以减少船舶水下辐射噪声对海洋生物的不利影响。而降低辐射噪声的关键就在于确定主要源的位置和辐射特性等，从而有针对性地拟订噪声控制方案，有效控制辐射噪声。噪声源成像技术对确定主要的辐射源位置和辐射特性等具有重要的实用价值，时间反转（Time Reversal，TR）方法可实现声波的反向传播和自适应聚焦，可用于声源成像。时间反转法利用了线性化波动方程中只包含声压对时间的二阶导数这个特点，这样p(r,t)和p(r,-t)就都是波动方程的解，其中p(r,t)代表由声源向外辐射正向传播的声场，而p(r,-t)则代表反向传播（即向声源传播并汇聚于声源的声波）的声场。时域中的时间反转等价于频域中的相位共轭（Phase Conjugation，PC）［1］，即p(r,t)和p(r,-t)等价于p(r,ω)和p*(r,ω)，同样p(r,ω)为正向传播的声场，p*(r,ω)为反向传播的声场。时间反转过程就是将接收到声源发射的时域信号在时间上反转（先到的后发，后到的先发），再从相应的发射器发射出去，发射出的信号将在原声源处聚焦。所以，在使用换能器阵列测得声源正向传播的声场后，可以基于特定的时间反转（相位共轭）方法实现声源的成像。

多数时间反转方法基于换能器阵测量并记录声压信号，然后时间反转（或相位共轭）。从能量聚焦角度，采用测量声压场并用单极子源构建时间反转（或相位共轭）场，达到自适应聚焦，在时域称其为TR/M阵。Helmholtz-Kirchhoff积分公式表达了可以将声源取代为其表面上声压和法向速度的分布（或单极子和偶极子的分布），声场可由一个闭合波面上的声压及其梯度的积分得到。依据Helmholtz-Kirchhoff积分公式，测量声压p(rn,ωs)和声压梯度分别使用偶极子源和单极子源来进行相位共轭的处理，在时域称其为TR/P。De Rosny和Fink［2］对3种时间反转（相位共轭）阵列进行了研究，分别是上文提到的TR/M阵，TR/P阵以及基于测量声压梯度使用偶极子源来进行时间反转的TR/D阵。其结论是：TR/P阵列形成的时间反转（相位共轭）声场完全不包含倏逝波，不能突破衍射极限分辨率（不管该阵列离声源有多近）；TR/M阵列形成的时间反转（相位共轭）声场包含倏逝波，但不能突破衍射极限分辨率；TR/D阵列形成的时间反转（相位共轭）声场包含倏逝波，且能突破衍射极限分辨率。Fannjiang［3］对各种时间反转镜（阵列）的聚焦特性进行了详尽的分析，指出只要使用声压梯度测量或是使用偶极子源发射就能突破衍射极限分辨率。

由于线列阵的实际应用广泛，而前人并没有针对不同形式相位共轭线列阵的相关参数对噪声源聚焦成像的影响进行研究。故本文将对相位共轭阵列及其形成的相位共轭声场的理论研究成果进行系统的梳理和分析；同时，通过数值仿真比较研究3种相位共轭线列阵，即基于测量声压使用单极子源的相位共轭阵列（PC/M），基于测量声压梯度使用偶极子源的相位共轭阵列（PC/D）和基于测量声压和质点速度使用单极子源和偶极子源的相位共轭阵列（PC/P）；在不同阵列形式和阵元间距的情况下，在近距离测量中从对聚焦成像效果的影响角度讨论，同时考虑阵元的小偏移对聚焦的影响，所得结论可为实际应用提供参考。

1 理论和分析

1.1 相位共轭阵列PC/P产生的声场与正向传播声场p(r)及其复共轭声场p*(r)的关系

考虑自由空间中一个一般形状声源f的声辐射问题。声场满足有源Helmholtz方程：

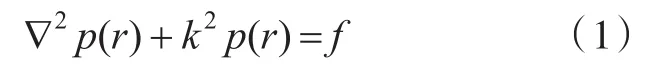
式中：p为声压；k为波数。由Helmholtz-Kirch⁃hoff积分公式，可知空间中任一点r处的声压为［4］

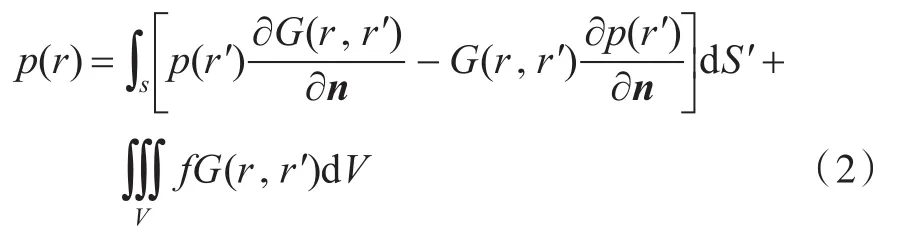
式中：积分表面S为包围声源的封闭表面；V为表面S包围的体积。为自由场格林函数，R= |r-r′|；n为S的外法向单位矢量。

设测量阵列分布在距离该声源一定距离并包围声源的封闭表面S上，在阵列测量到声源辐射的声压和声压梯度后，移除初始声源，将各阵元测到的声压和声压梯度进行复共轭，依据式（2）中的面积分项，得到测量面S的相位共轭声场为［1］

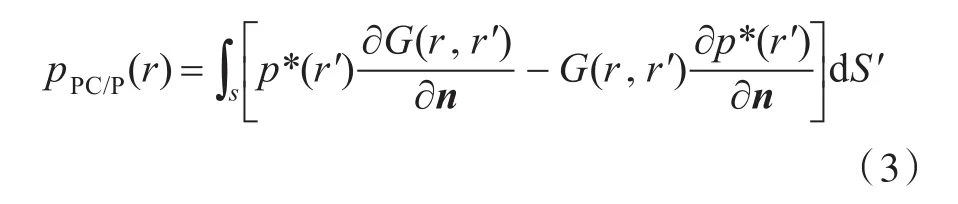
应该指出的是，pPC/P(r)≠p*(r)，也就是这种情况下的相位共轭声场pPC/P(r)并不等于声源向外辐射正向传播声场p(r)的复共轭声场p*(r)。此时，pPC/P(r)与p*(r)的关系为［3］

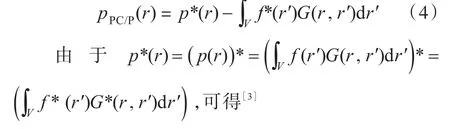
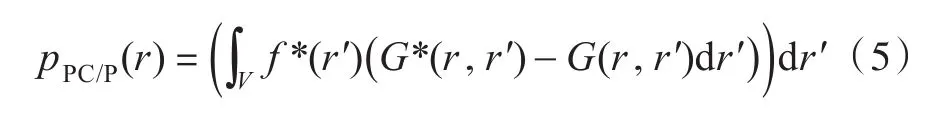
上式表明，相位共轭声场pPC/P(r)可以理解为是由源f*(r′)和格林函数产生的声场。引入声汇后（在有声汇的情况下）［5］，式（5）中的格林函数变 为当ρ=1时，格林函数为G*(r,r′)，此时相位共轭声场pPC/P(r)等于声源向外辐射正向传播声场p(r)的复共轭声场p*(r)，互为共轭的声场如图1所示。

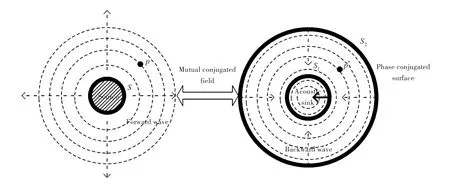
图1 互为共轭、传播方向相反的p(r)和p*(r)Fig.1 p(r)andp*(r)are mutually phase-conjugated and spread in the opposite direction

1.2 PC/P，PC/M和PC/D的关系

在无限自由空间，距离声源远处，声压p(r)和格林函数G(r,r′)的法向导数可以表示为：

从上面的推导可以看出，式（8）和式（9）可由式（3）在远场或平面波近似下得到。

实际的相位共轭阵列都是离散的，对包含N个阵元的离散的有限阵列，与式（3）对应的相位共轭声场可表示为

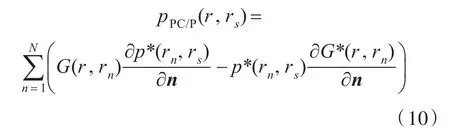
如基于测量声压使用单极子源来进行相位共轭，与式（8）对应（省略了前面的乘积项）的相位共轭声场为

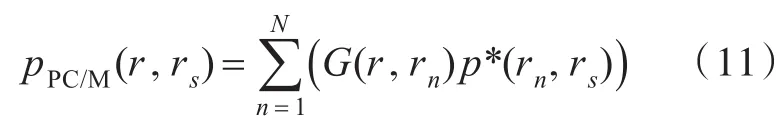
相位共轭阵列PC/M产生的声场也可理解为由阵元位置处各个点源（点源强度为阵元测得的声压p(r)的复共轭声压p*(r)）组成的组合声源产生的声场，相位共轭阵列PC/M产生的相位共轭声场满足Helm⁃ holtz微分方程

如基于测量声压梯度使用偶极子源来进行时间反转，与式（9）对应（省略了前面的乘积项）的相位共轭声场为

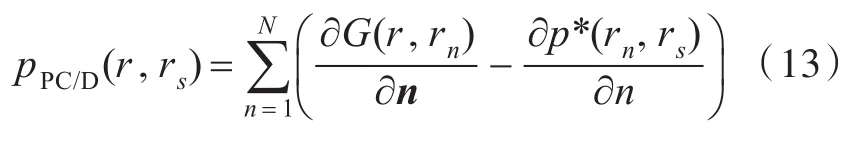
1.3 相位共轭声场的倏逝波和传播波分析

波动方程的稳态平面波解有2类：一类是普通的平面波，另一类是倏逝波［5-6］。在波数域中，当波矢分量(kx,ky)落在以波数k为半径的圆面内时，其对应普通平面波（即传播波）；而当(kx,ky)落在以k为半径的圆面外时，kz为虚数，此时其对应的是倏逝波。在波数域中，可以很清楚地看到组成该声场的各平面波分量，选择波数积分中的不同区域，如使(kx,ky)落在以k为半径的圆面内，就得到传播波声场，使(kx,ky)的积分区域落在以k为半径的圆面外，则得到倏逝波声场。倏逝波在传播方向的相速度比声速小，幅度在与传播方向垂直的方向上以指数形式衰减。倏逝波只对近场声压有贡献，而传播波对近场声压和远场声压都有贡献，在远场只能测到传播波。由于倏逝波是幅值随传播距离按指数规律衰减的高波数声波，在一个波长以上就可以忽略了，所以对倏逝波声场的测量只有在近场才能保证，一般要求测量距离在1/3最小波长以下。

由Weyl公式［4］，自由场格林函数的球面波表示为平面波的叠加：

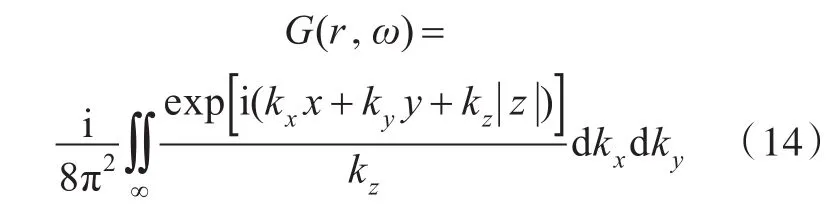
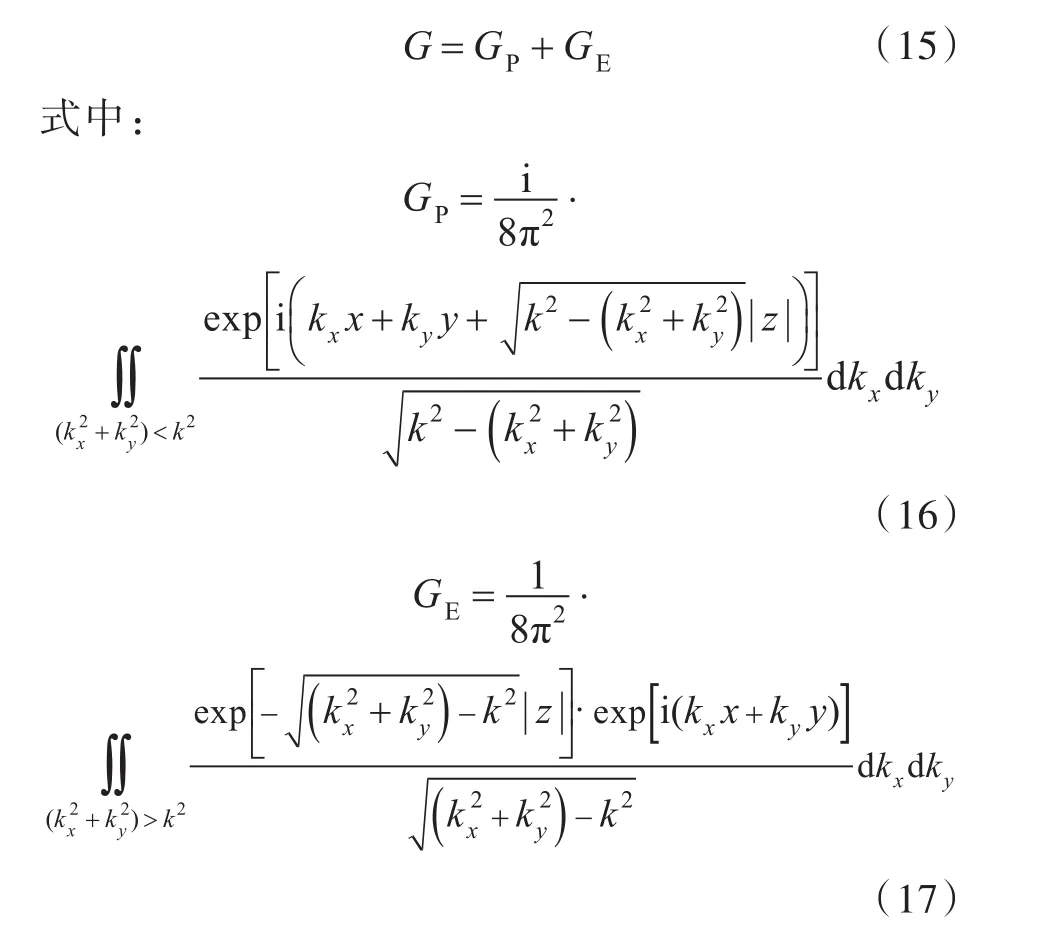
由式（17）可知，倏逝波不是复振幅，而是实数振幅，其幅值在与传播方向垂直的z方向上以指数形式衰减。

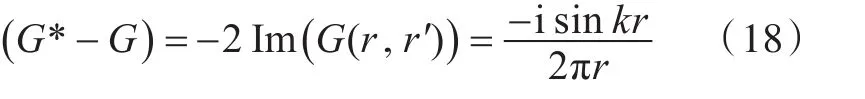
相位共轭阵列PC/M所产生声场的格林函数就是自由场格林函数式（14），所以PC/M的相位共轭声场包含倏逝波。

相位共轭阵列PC/D所产生声场的格林函数为

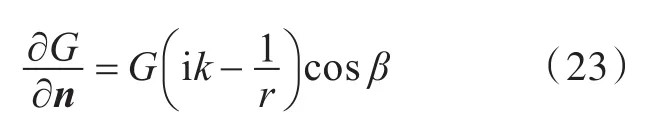
式中，β为n与r的夹角。PC/D的相位共轭声场包含倏逝波。

1.4 相位共轭声场的聚焦特性

相位共轭声场的聚焦特性可用峰值高度一半时的宽度，即“半高宽”或“半峰宽”（Full Width at Half Maximum，FWHM）来表征［3］。

Harker和Anderson［7］使用源点声压幅值与场点声压幅值平均值的比值（Source to Field Ratio，SFR）来表征相位共轭声场的聚焦特性：

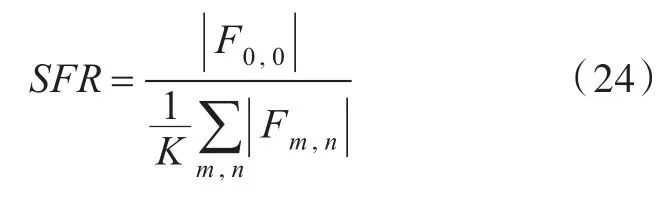
式中：|F0,0|为源点声压幅值；|Fm,n|为场点声压幅值；K为场点个数。当SFR=1时看不出聚焦，SFR值越大说明聚焦越强。

1.5 相位共轭阵列的阵元间距

阵列辐射的声场是各个阵元辐射的叠加，当信号源在不同方向时，由于各阵元接收信号与基准矢量的相位差不同，导致输出的幅度不同从而使阵列具有指向性［8］。对于线列阵，当中心非模糊扇面要求为+90°时，通常要求阵元间距小于1/2波长［8］。对于相位共轭阵列，Fink等［9］指出，阵元间距不应超过1/2波长以避免混叠旁瓣。Harker等［7］以圆周上闭合的相位共轭阵列在源点位置处产生的声压幅值与在源点周围场点声压幅值的平均值的比值SFR作为聚焦特性指标对半空间中的相位共轭阵列参数进行了研究，指出聚焦特性取决于阵列相对于源位置的角密度，而不是阵元的间距，阵元间距远大于1/2波长时也可取得最佳效果。当角密度不变时，增大阵列的孔径可以增强成像能力。由于本文讨论的测量距离包含近场，阵列的相关参数对聚焦的影响是否与远场指向性的特点相一致还有待讨论。

以点声源（图2）为例，在无限均匀时不变空间中，参考弗朗霍夫远场近似［4］，有

图2 阵列示意图Fig.2 The sketch map of array

式中，d为阵元间距。将式（25）与式（26）代入式（11）中，得

将θw看作主瓣宽度的度量［4］，它决定分辨率的大小。L=（N-1）d，为阵列长度。由式（29）可以看出，当阵元间距d和阵列长度L相比不可忽略时，聚焦分辨率与频率、阵元间距、阵列长度、声源方位角有关。本文讨论阵元长度一定时，阵元间距和阵元个数对聚焦效果的影响。

2 数值结果和分析

本节对相位共轭阵列PC/M，PC/D和PC/P产生的相位共轭声场近场聚焦特性进行数值计算研究。相位共轭阵列的形式采用等间距线阵列，线阵列长度为L，阵列测到的声场是由位于直角坐标系oxyz原点o的点声源产生的，讨论阵列长度一定，不同阵元间距对聚焦效果的影响。其中：f=100 Hz，c=350 m/s，λ=3.5 m，A=1。

2.1 基于FWHM的聚焦特性分析

线阵列长度L=2λ，分别使用3，5，9和17个阵元进行相位共轭声场计算，相应的阵元间距分别为λ，λ/2，λ/4和λ/8。计算阵列距离点声源的垂直距离为z=0.01λ，0.1λ，0.2λ，2λ和5λ时的FWHM，如表1所示。z=0.01λ，0.1λ，2λ和5λ时在阵元间距为λ/2情况下x=0～2λ（y=z=0）间的相位共轭声场归一化幅值如图3～图7所示。

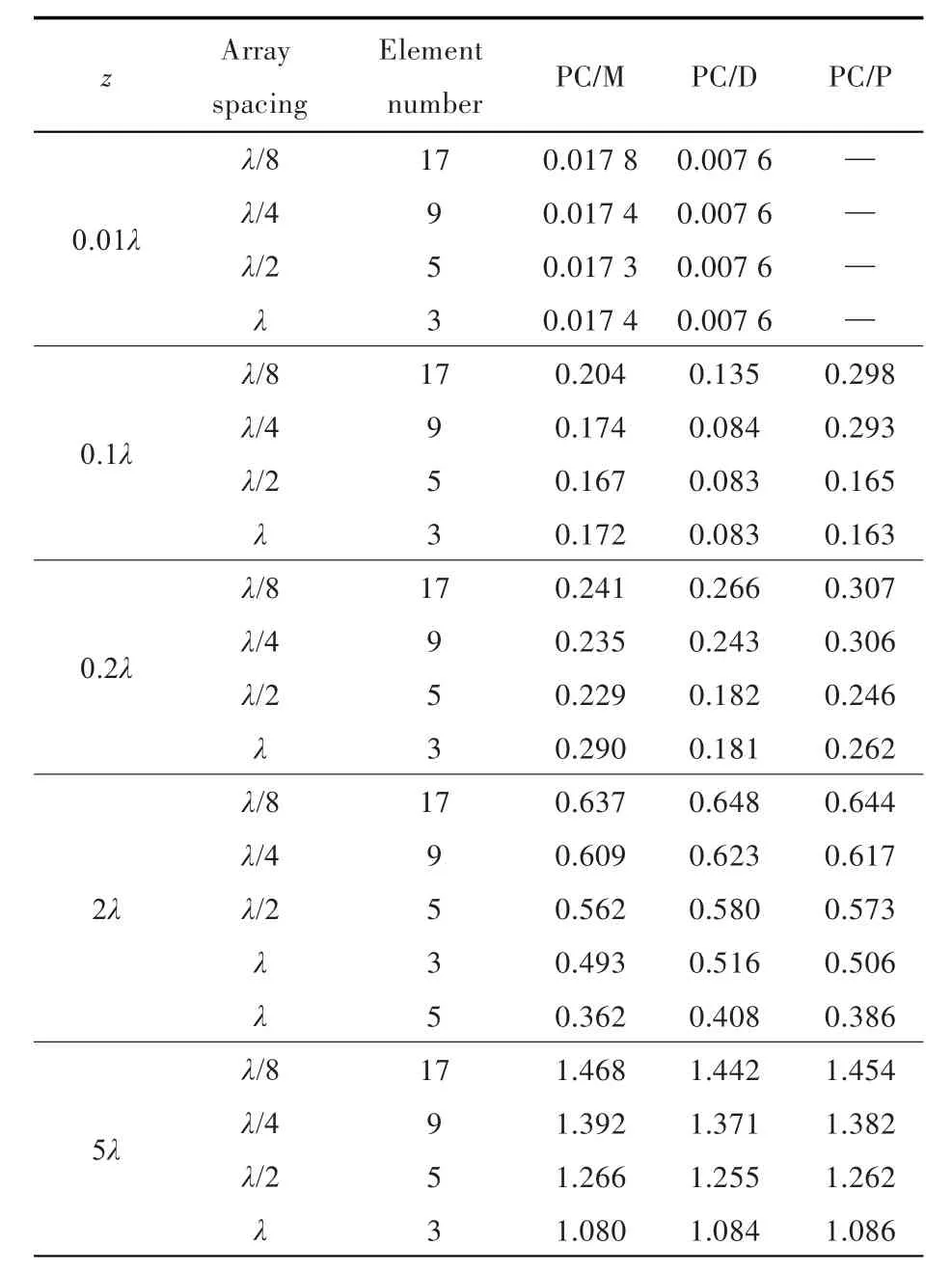
表1 不同距离和不同阵元间距情况下的FWHMTable 1 FWHM of different distance and different element spacing

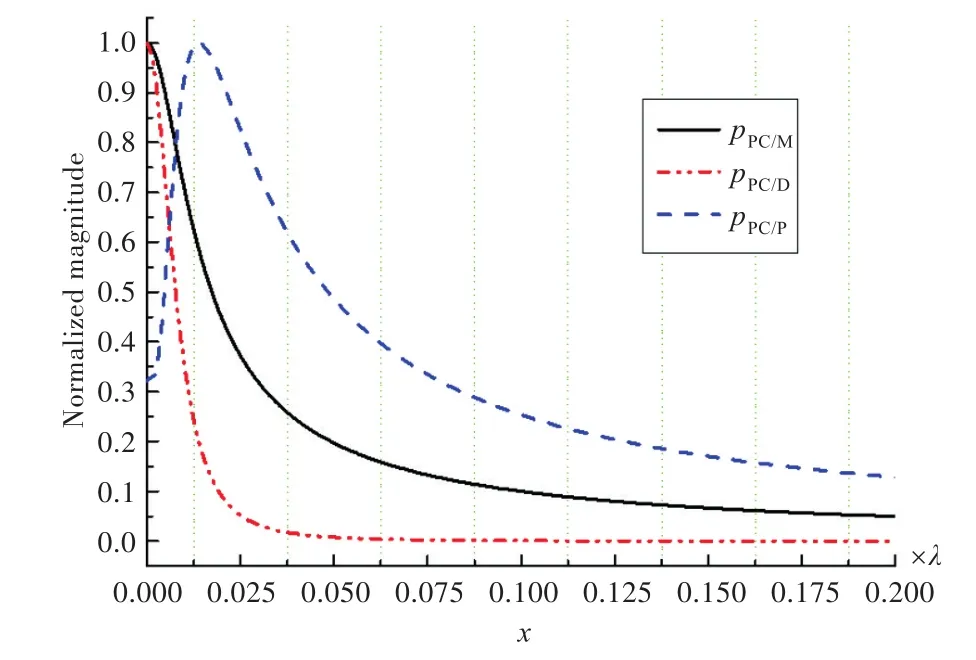
图3 z=0.01λ且阵元间距为λ/2情况下的相位共轭声场Fig.3 Phase-conjugate field ofz=0.01λandλ/2 element spacing

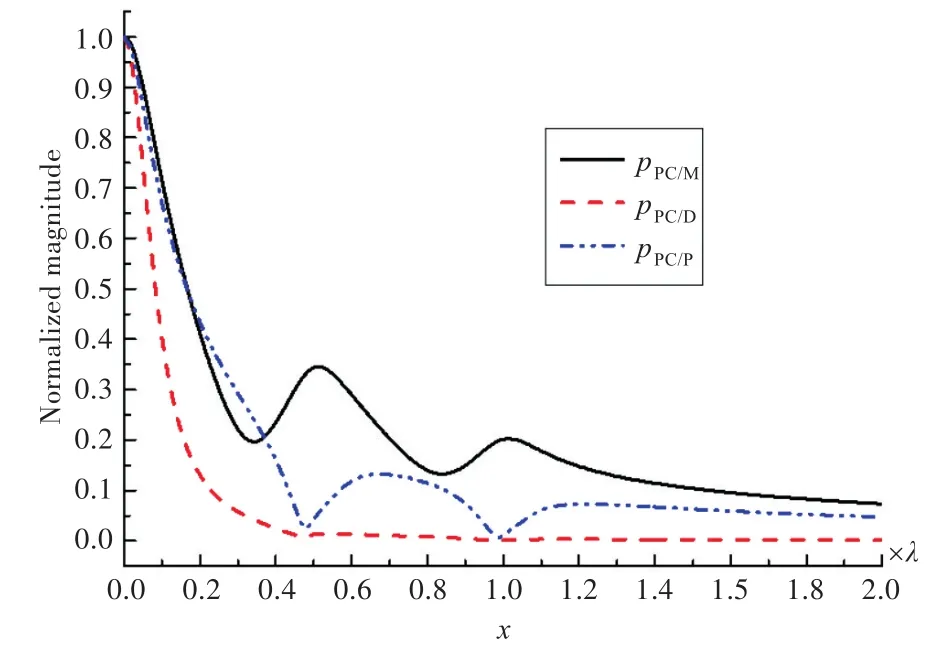
图4 z=0.1λ且阵元间距为λ/2情况下的相位共轭声场Fig.4 Phase-conjugate field ofz=0.1λandλ/2 element spacing

图5 z=2λ处不同阵元间距相位共轭阵聚焦效果对比Fig.5 Comparison between different element spacing of phase-conjugate array atz=2λ

由表1、图3和图4可知：在倏逝波不被忽略的距离内，PC/D阵列的聚焦性能最强，且λ/2阵元间距与λ阵元间距差别不大；PC/P阵列在z=0.01λ时失效；随着阵与点声源距离的增加，PC/M阵列聚焦显出优势；随着z的增大，3种阵列的聚焦特性趋于一致，即阵距离源越远，不同相位共轭阵聚焦效果差别越小。图5图例中第1个数字表示阵元间距几倍波长，下划线后面的数字表示阵元个数。从图5可以看到，距离声源z=2λ处，当阵列长度一定时，阵元间距增大，阵元个数减少，聚焦半峰宽虽然变窄，但对应的旁瓣增大了。即在阵列长度一定的情况下，半峰宽与旁瓣抑制不可兼得，提高聚焦空间分辨率要以牺牲旁瓣抑制为代价。当阵元间距确定为1倍波长时，增加阵元个数即阵长度增加，不但能使半峰宽变窄，而且旁瓣抑制也较好；当阵列长度L=2λ时，半波长的相位共轭处理在聚焦精度上较差，但旁瓣抑制最好；相同阵列参数下PC/M的聚焦精度高，PC/D的旁瓣抑制好。综上所述，旁瓣抑制以半波长间距的PC/D为好，聚焦精度以1倍波长的PC/M为佳。由表1和图6可知，在z=5λ的情况下，相位共轭阵列PC/M，PC/D和PC/P产生的相位共轭声场已趋于一致，且阵元间距为λ时聚焦分辨率最优。

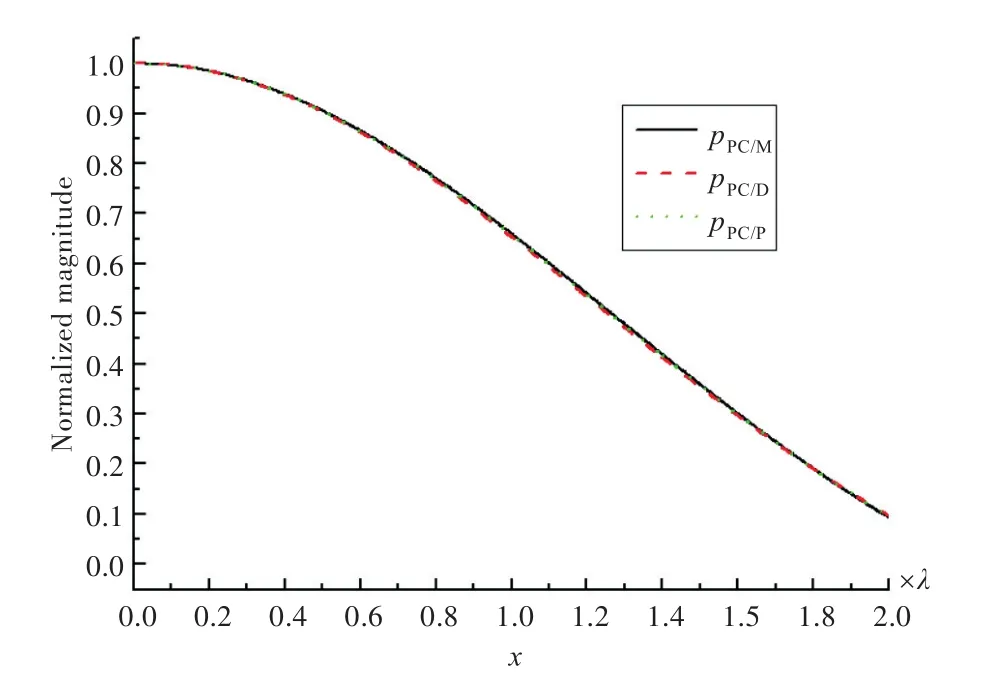
图6 z=5λ且阵元间距为λ/2情况下的相位共轭声场Fig.6 Phase-conjugate field ofz=5λandλ/2element spacing

在线阵列长度L=24λ情况下，图7～图9、图11、图13和图14分别以λ/2，λ，2λ和4λ阵元间距（对应使用50，25，13和7个阵元）进行相位共轭声场计算。图10示出了阵元间距为λ/4情况下，50个阵元的PC/M相位共轭场。图12示出了阵元间距为λ，50个阵元的PC/M相位共轭场。

计算线阵列距离点声源的垂直距离为z=13λ时，的正方形区域内场点（场点间距为0.05λ，共481×481=231 361个场点）的声压幅值云图，如图7～图14所示。

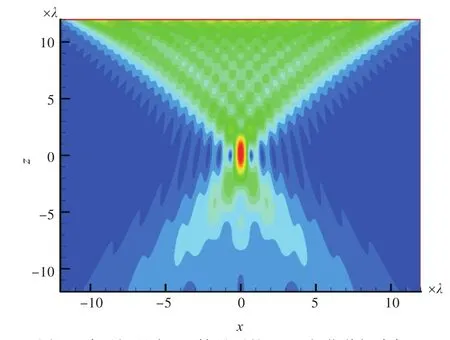
图7 阵元间距为λ/2情况下的PC/M相位共轭声场Fig.7 PC/M phase-conjugate field ofλ/2element spacing

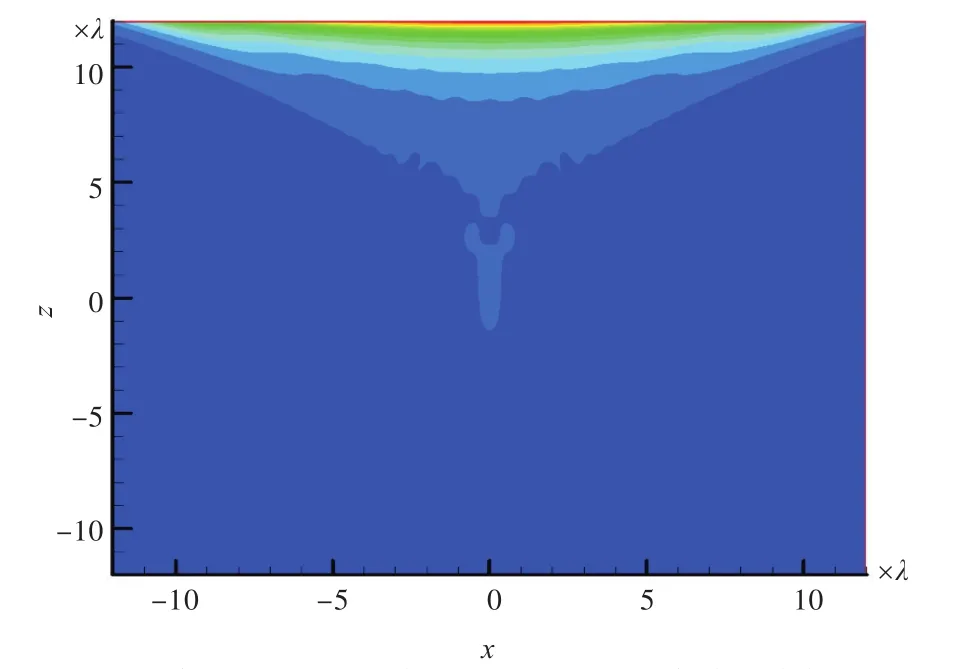
图8 阵元间距为λ/2情况下的PC/D相位共轭声场Fig.8 PC/D phase-conjugate field ofλ/2element spacing

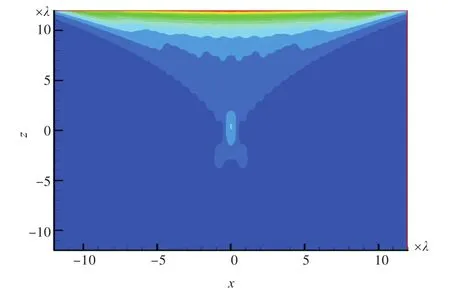
图9 阵元间距为λ/2情况下的PC/P相位共轭声场Fig.9 PC/P phase-conjugate field ofλ/2element spacing

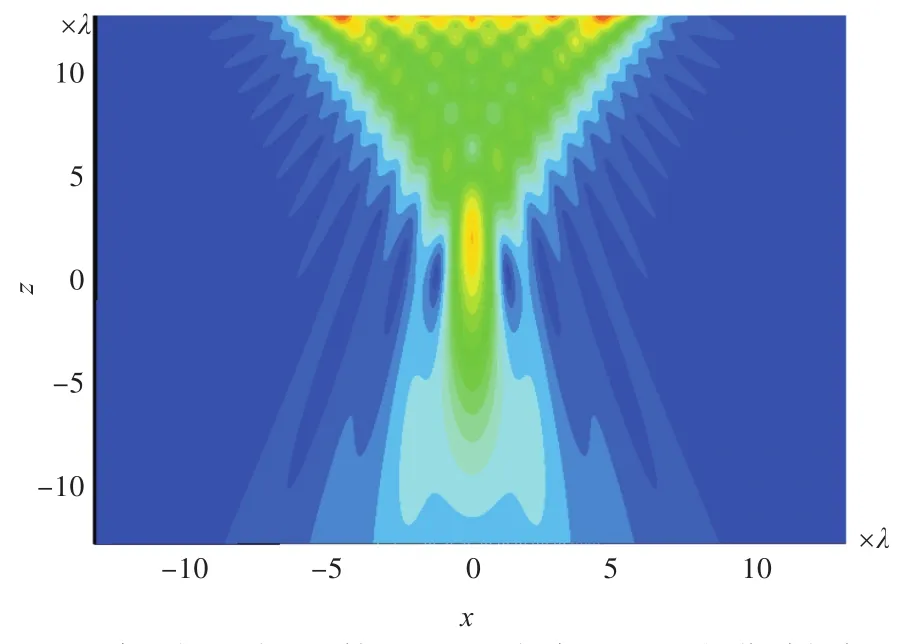
图10 阵元间距为λ/4情况下，50个阵元PC/M相位共轭场Fig.10 PC/M phase-conjugate field ofλ/4element spacing for 50 elements

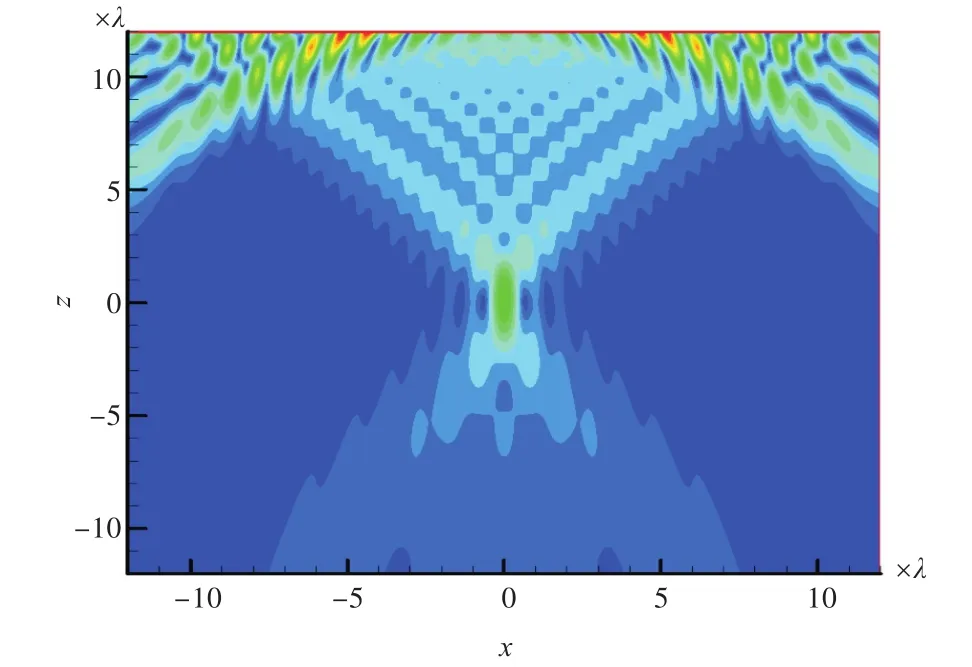
图11 阵元间距为λ情况下的PC/M相位共轭声场Fig.11 PC/M phase-conjugate field ofλelement spacing

由图7～图9可知，在阵列参数相同的情况下，PC/M阵列形成的相位共轭声场聚焦效果最好；对比图7、图11～图14可知，在距离声源13λ处，在阵列长度相同情况下，间距为λ/2时，PC/M阵列聚焦效果最好，当阵元间距增大后，聚焦效果变差，阵元间距增大到4λ时声源处聚焦已不太明显；对比图11与图12可知，当阵元间距不变、阵元个数增加1倍、阵列长度增大时，聚焦效果变好；对比图12与图7可知，相同阵元个数的情况下，λ/2间距的PC/M阵列聚焦效果好。可见，阵元间距的选择比阵元个数的确定对聚焦效果更加重要。综上分析，在远距离处阵元间距为λ/2的PC/M阵列聚焦效果最好。在远距离处，增加阵列长度能够增强聚焦，但阵元间距的选择更为重要，以λ/2阵元间距为佳。

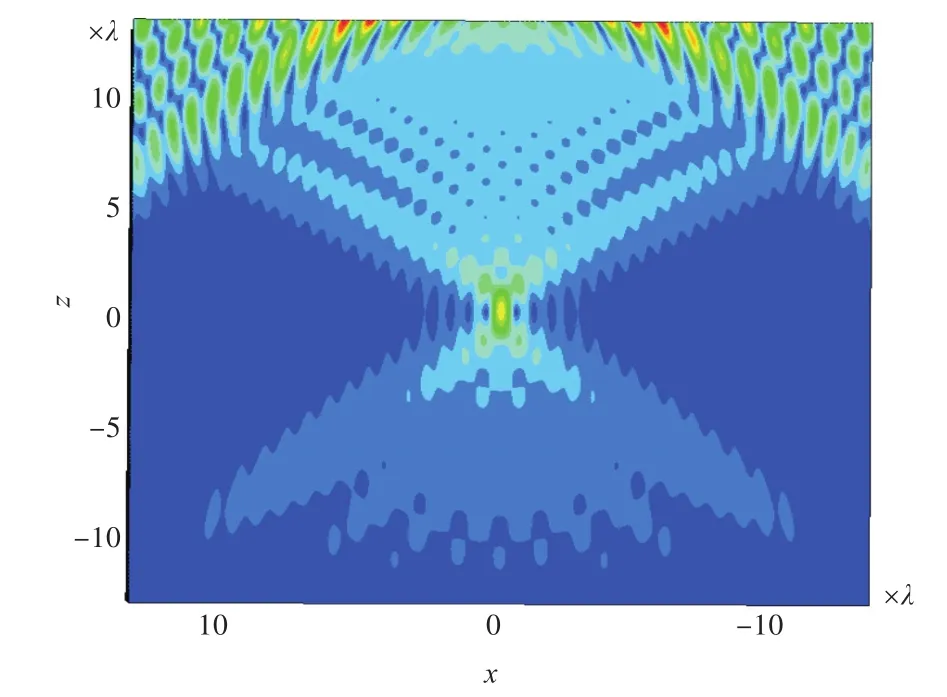
图12 阵元间距为λ，50个阵元PC/M相位共轭场Fig.12 PC/M phase-conjugate field ofλelement spacing for 50 elements

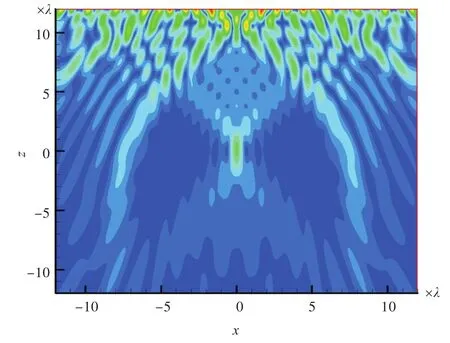
图 13 阵元间距为2λ情况下的PC/M相位共轭声场Fig.13 PC/M phase-conjugate field of2λelement spacing

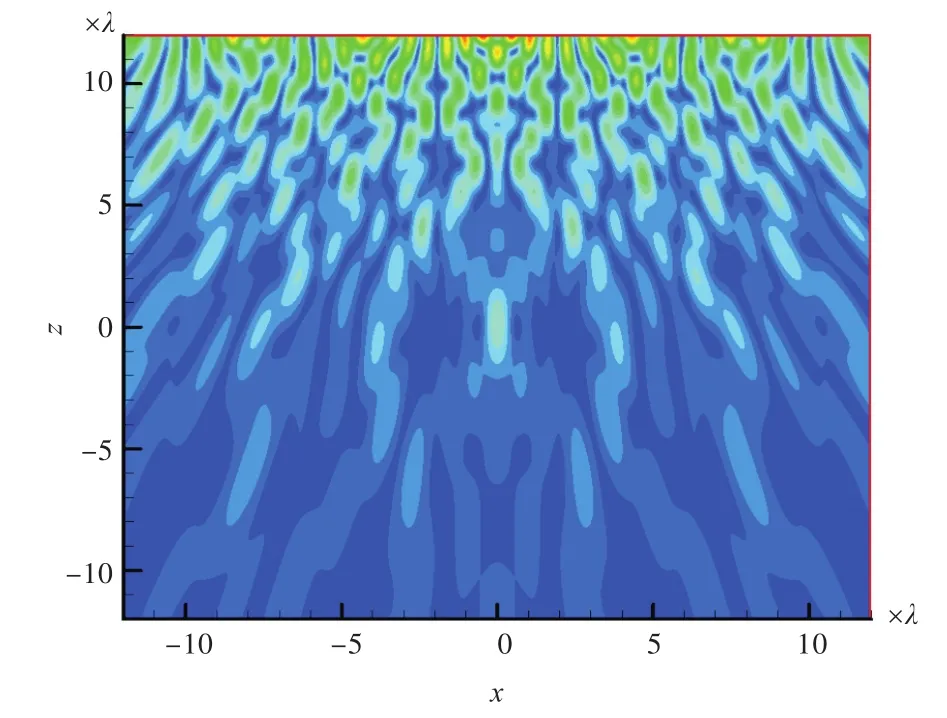
图14 阵元间距为4λ情况下的PC/M相位共轭声场Fig.14 PC/M phase-conjugate field of4λelement spacing

2.2 阵列偏移对聚焦效果的影响

由于海洋环境复杂多变，线阵元的位置在实测海况中可能出现偏差，本节讨论阵元的偏移对聚焦效果的影响。阵顶端固定，从线列阵中间位置阵元开始，将线列阵的一半阵元进行人为偏移，以Δrn表示阵元偏移量，ΔRS表示聚焦峰值与实际源位置的偏差。表2示出了在阵距离点声源0.2λ处，不同阵元间距下，阵元偏移量对聚焦的影响。表3示出了在阵距离点声源2λ处，不同阵元间距下，阵元偏移量对聚焦的影响。表3皆是5元阵。图15与图16示出了在阵距离点声源0.2λ、阵元偏移0.1 m情况下，不同阵元个数以及不同阵元间距的相位共轭阵产生的声场的对比。图17示出了在阵距离点声源0.2λ和2λ处、λ/2阵元间距、阵元偏移0.1 m情况下相位共轭阵聚焦效果的对比。

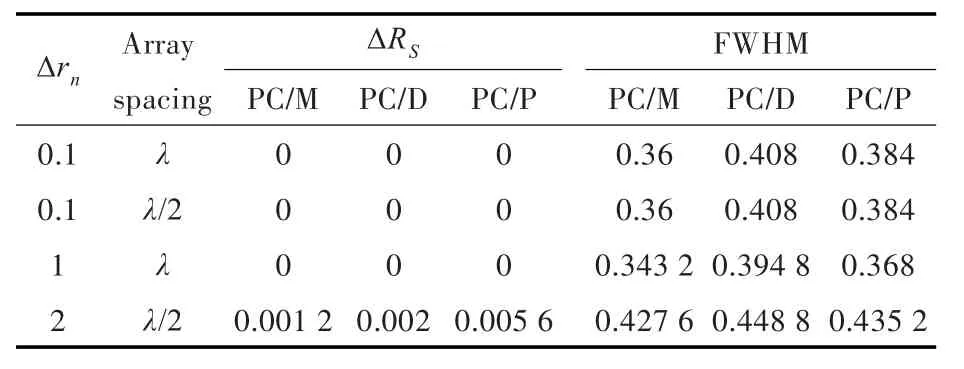
表2 z=0.2λ处聚焦峰值与实际位置偏差表Table 2 Focusing peak in comparison with the actual position atz=0.2λ

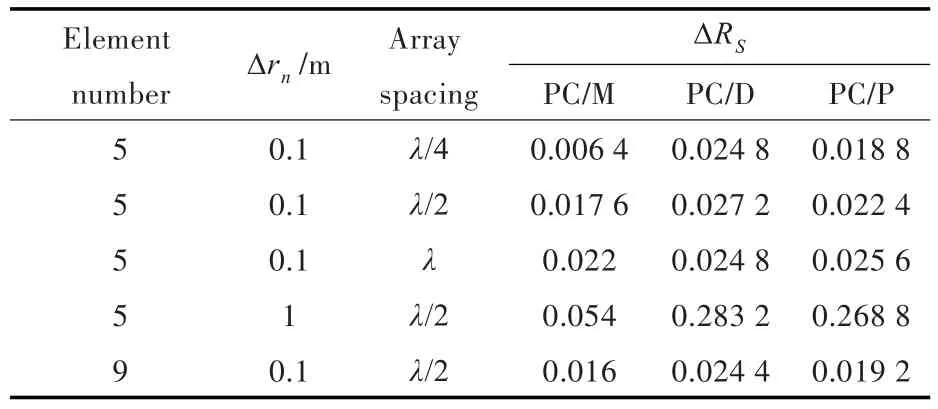
表3 z=2λ时，阵元偏移量对相位共轭阵聚焦效果的影响Table 3 Influence of different element deviation on phaseconjugate array focusing effect atz=2λ

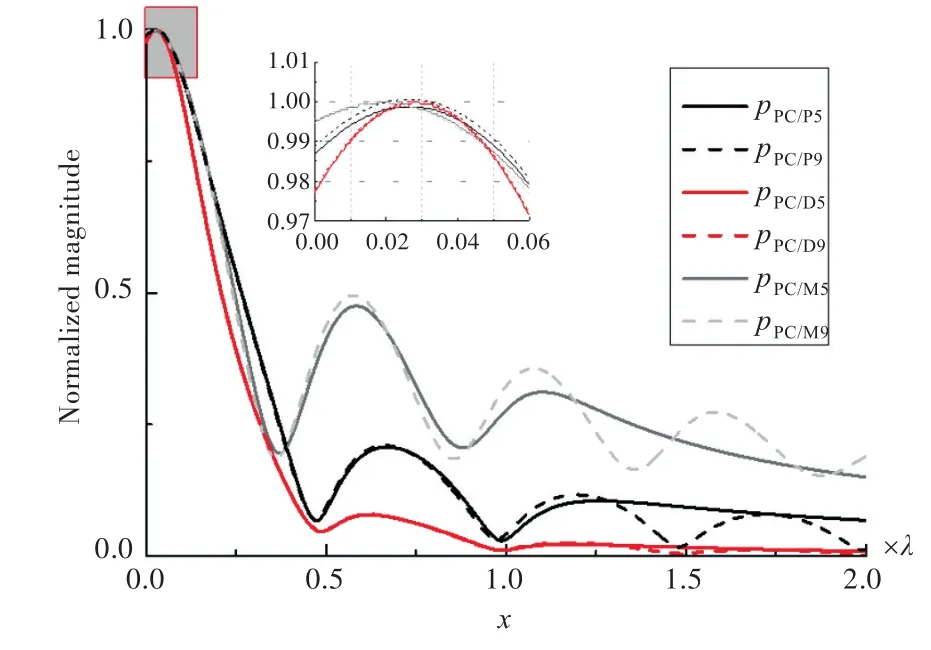
图15 不同阵元个数的相位共轭阵聚焦效果对比Fig.15 Focusing effect comparison of different element numbers

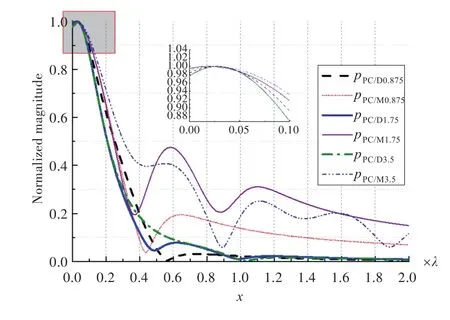
图16 不同阵元间距的相位共轭阵聚焦效果对比Fig.16 Focusing effect comparison of different element spacing

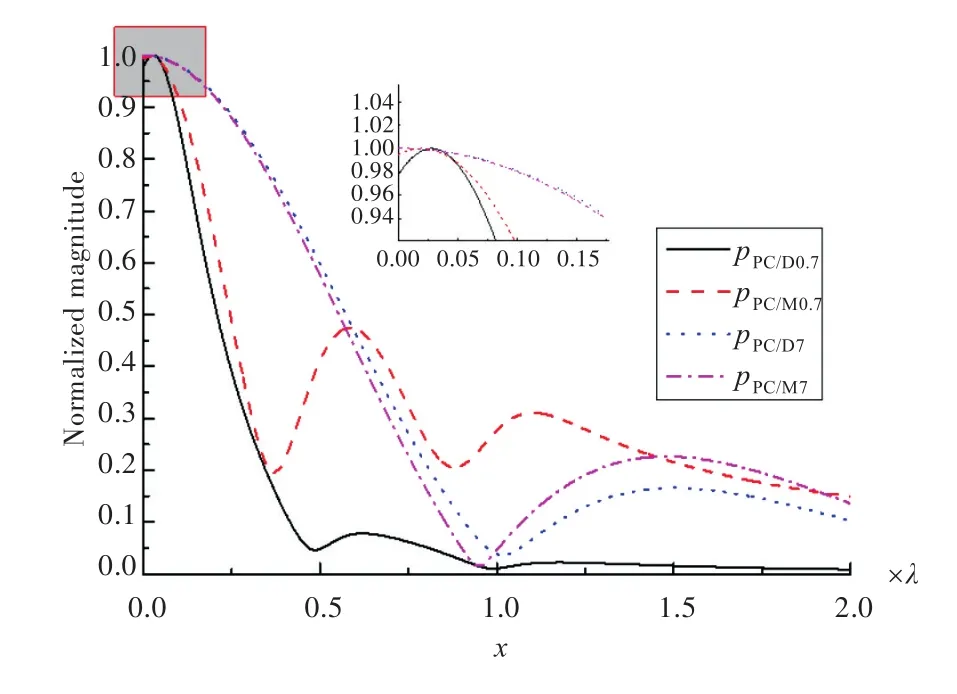
图17 相位共轭阵距离点声源不同位置处的聚焦效果对比Fig.17 Focusing effect in comparison of different distances

图15图例中下标5和9分别表示5个阵元和9个阵元。比较发现，阵元个数增加对聚焦效果的改善并不明显。图16图例中下标的数字表示阵元间距，是不同阵元间距的PC/D与PC/M相位共轭阵聚焦效果对比。从半峰宽和旁瓣抑制角度看，λ/2阵元间距的PC/D相位共轭阵聚焦效果最好；对比表2数据，λ/2阵元间距的PC/D相位共轭阵聚焦位置的偏移比PC/M稍大。

图17图例中下标的数字表示相位共轭阵与点源的距离。在有阵元偏移的情况下，增加阵与点源的距离，不同阵列方式聚焦效果趋于一致。

阵元偏移会影响聚焦效果，体现在焦点偏移和半峰宽增大。在焦点偏移方面，PC/M焦点偏移小，随着阵元间距的增加，焦点偏移增大。阵元偏移量的增大也会增加焦点偏移量。增加阵元个数会改善焦点偏移。在旁瓣抑制方面，由图15和图16可知，PC/D旁瓣抑制效果好，以λ/2阵元间距的PC/D聚焦效果为佳。

对比表2和表3发现：当增大阵与源的距离时，阵元偏移对聚焦位置的影响变小，同时各种阵列方式聚焦效果趋于一致；当阵元偏移相对阵与源的位置较小时，聚焦位置基本无偏差；增加阵元个数能够改善偏移对聚焦位置的影响，但阵元间距的选择更重要。

综上所述，在极近距离处(z=0.01λ)，PC/P失效。在能测到倏逝波的距离内，考虑阵列存在偏移的情况，以半波长间距的PC/D效果最好。阵与源距离越远，3种阵聚焦效果越差，但阵的偏移对聚焦效果影响越小。随着阵与源距离的增加，3种相位共轭阵聚焦效果趋于一致，阵元间距半波长为最好。当阵与源的距离增加到倏逝波衰减至忽略的程度后，以半波长为阵元间距的PC/M阵聚焦效果最佳。

3 结 语

本文对PC/M，PC/D和PC/P这3种相位共轭阵列及其形成的相位共轭声场的理论进展进行了系统的梳理和分析：对相位共轭阵列PC/P产生的声场与声源正向传播声场p(r)及其反向传播的复共轭声场p*(r)的关系进行了推导；对相位共轭阵列PC/P，PC/M和PC/D之间的关系进行了推导；对相位共轭声场的倏逝波和传播波进行了分析；对描述相位共轭声场聚焦特性的指标、相位共轭阵列的阵元间距与聚焦特性的关系进行了说明。基于线阵列对相位共轭阵列聚焦特性的数值仿真结果表明：在能够测得倏逝波的范围内，PC/D阵列聚焦效果最好，陈元间距在一倍波长内变化时，不同阵元间距对阵列聚焦的影响不大。在几倍波长距离处，在阵元间距与阵长相比不可忽略时，阵元间距增大，可缩小半峰宽度，代价是旁瓣干扰增大。在阵距离声源较远处，阵元间距为λ/2的PC/M阵列的聚焦性能最好。

［1］ JACKSON D R，DOWLING D R.Phase conjugation in underwater acoustics［J］.The Journal of the Acoustical Society of America，1991，89（1）：171-181.

［2］ DE ROSNY J，FINK M.Focusing properties of nearfield time reversal［J］.Physical Review A，2007，76（6）：065801.

［3］ FANNJIANG A C.On time reversal mirrors［J］.In⁃verse Problems，2009，25（9）：095010.

［4］ 张海澜.理论声学［M］.2版.北京：高等教育出版社，2007.

［5］ DE ROSNY J，FINK M.Overcoming the diffraction limit in wave physics using a time-reversal mirror and a novel acoustic sink［J］.Physical Review Letters，2002，89（12）：124301.

［6］ WILLIAMS E G.Fourier acoustics：sound radiation and nearfield acoustical holography［M］.San Diego：Academic Press，1999.

［7］ HARKER B M，ANDERSON B E.Optimization of the array mirror for time reversal techniques used in a half-space environmen［tJ］.The Journal of the Acousti⁃cal Society of America，2013，133（5）：EL351-EL357.

［8］ 田坦，刘国枝，孙大军.声呐技术［M］.哈尔滨：哈尔滨工程大学出版社，2000.

［9］ FINK M，PRADA C.Acoustic time-reversal mirrors［J］.Inverse Problems，2001，17（1）：R1-R38.

Phase-conjugate arrays and phase-conjugated fields produced by the arrays

LI Sheng1，2，LI Ting1，2，LIU Song1，2

1 School of Naval Architecture Engineering，Faculty of Vehicle Engineering and Mechanics，Dalian University of Technology，Dalian 116024，China

2 State Key Laboratory of Structural Analysis for Industrial Equipment，Dalian University of Technology，Dalian 116024，China

Phase Conjugate（PC）arrays can make sound waves travel backwards to converge，which can then be used to build the image of a noise source.This paper reviews and analytically studies three types of PC array（monopole PC array（PC/M），dipole PC array（PC/D）and perfect PC array（PC/P））and the phase-conjugated fields produced by the arrays.The relationship between the sound field produced by the source and the phase-conjugated fields produced by the arrays are discussed.The various PC schemes are compared and analyzed from the evanescent wave component and the propagating wave component.The metrics of the focusing properties of PC arrays and the effects of the array element spacing on the focusing properties are discussed.The spatial resolutions of various PC schemes with different distances between array and source are studied numerically with linear arrays.The element deviation is also discussed.A numerical simulation shows that PC/D with half-wavelength element spacing is effective at near field focusing，and PC/M with half-wavelength element spacing is effective at a greater distance.

phase-conjugate arrays；phase-conjugated fields；evanescent wave；focusing properties

U666.74

A

10.3969/j.issn.1673-3185.2017.01.016

2015-11-16

2016-12-28 16:14

辽宁省教育厅重点实验室基础研究项目（LZ2014004）

黎胜，男，1973年生，博士，教授，博士生导师。研究方向：船舶与海洋结构物振动噪声机理、预报与控制。E-mail：shengli@dlut.edu.cn李婷（通信作者），女，1985年生，博士生。研究方向：噪声源识别和定位及声场重构。E-mail：litingyouxiang@sina.com

http://www.cnki.net/kcms/detail/42.1755.TJ.20161228.1614.042.html期刊网址：www.ship-research.com

黎胜，李婷，刘松.相位共轭阵列及其形成的相位共轭声场［J］.中国舰船研究，2017，12（1）：107-115，133. LI S，LI T，LIU S.Phase-conjugate arrays and phase-conjugated fields produced by the arrays［J］.Chinese Journal of Ship Research，2017，12（1）：107-115，133.