基于ICCP算法的重力匹配仿真*
2017-01-11蔡龙飞
蔡龙飞 郑 彤
(海军驻武汉四三八厂军事代表室 武汉 430064)
基于ICCP算法的重力匹配仿真*
蔡龙飞 郑 彤
(海军驻武汉四三八厂军事代表室 武汉 430064)
利用地球物理场进行辅助匹配导航是组合导航技术研究领域的新方向,该技术为水下潜器无源定位提供新的手段。迭代最近等值线算法作为重要的匹配导航算法之一,但存在实时性不强、搜索速度慢等缺点。考虑到以上两方面缺点,采用固定初始序列长度的方式对算法采样结构进行改善并推导出单点迭代公式,同时采用滑动窗搜索方式缩小搜索范围提高算法速度,最终实现实时ICCP算法设计。结果可以看出,该算法能够实现单点迭代,匹配结果能实时跟踪真实航迹。
迭代最近等值线算法;重力匹配;辅助导航;实时
(Military Representative Office in the 438th Factory, Wuhan 430064)
Class Number TP301
1 引言
海军潜艇作为国家重要的威慑力量和海上突击兵种,在高技术条件下海上局部战争中具有重要作用,同样科学技术的发展对海军潜艇的隐蔽性和续航能力提出了更高的要求。目前,潜艇水下导航主要采用惯性导航定位技术。然而,惯性导航系统定位误差随时间积累,无法长时间保持高精度。重力匹配辅助惯性导航技术具有完全自主性和高隐蔽性,能有效地对惯性导航系统误差进行水下重调校正,较好地满足潜艇长期隐蔽潜航的要求,是真正意义上的无源导航。该技术已经引起人们的极大关注,目前,美国、俄罗斯、澳大利亚和挪威等国已经对该项技术展开了深入研究[1~3]。
2 重力辅助惯导系统的原理
重力辅助导航系统是利用高分辨率的重力异常图组成的基本特征信息数据库,结合惯性导航系统给出的初始位置信息和海洋重力仪器提供的实测值,按照一定的匹配算法对惯性导航的初始位置进行校正,系统原理结构图如图1所示。
实测重力的具体位置信息,通常是以惯性导航的初始近似位置为基准,根据实际观测精度确定置信区间范围,提取已知的重力信息,并根据潜艇下潜深度进行重力异常的归算,将海洋重力实测的重力值和重力数据库提取的重力异常值归算到同一个计算面上,然后按照一定的算法估算出最佳匹配,将匹配结果反馈给系统用来改正导航误差。

图1 重力匹配辅助导航原理图
3 高精度重力场数据源基础
要进行重力场图形匹配,其首要条件就是要有高精度、高分辨率的重力背景场。从目前情况看,这个条件也已基本具备。各种高精度测高卫星的发射,如TOPEX、ERS-2、Envisat和Jason,已使从测高资料反演得到高精度和高分辨率的海洋重力场异常成为现实,目前已可以利用卫星测高资料反演获得分辨率为2’×2’的较高精度的海洋重力异常。我国测绘单位完成了中国海域的许多遂行测量任务,特别是完成国家相关专项任务之后,获得了许多重点海区高质量、高分辨率、高精度重力数据。中国海洋地质调查局、中油也进行了许多地区详细的重力调查,这些数据在进一步精化和融合的基础上可以得到进行重力匹配导航需要的重力数据基础。
4 重力图形匹配方法
重力图形匹配方法是进行重力场图形匹配的核心,简单地说就是通过实测重力与存储的重力数据进行匹配,实现对水下航行器的定位。算法的优劣直接影响到重力匹配辅助导航系统的定位精度、可靠性等重要指标。Behzed于1999年将图像对准算法中的迭代最近点算法应用到水下航行器的导航中[4],提出了迭代最近等值线算法,此后许多学者对ICCP算法进行了深入研究,并广泛应用于地形匹配、重力匹配、地磁匹配等辅助导航领域[5~11]。本文利用2′×2′卫星测高反演重力异常网格数据,ICCP匹配算法进行重新设计。
ICCP算法通过迭代计算、搜索最近点,实现测量值与背景场数据的最优匹配,从而获得位置信息,实现导航。基于背景场可以绘制等值线,若在航过程中某个历元的观测值为T,则该点的位置实际上在磁力值为T的等值线上,但无法确定其具体位置。为了确定该位置,需借助INS提供的推算位置,缩小搜索空间,并利用ICCP获取其实际位置。ICCP基于3点实现真实航迹的获取:
1) 实际航迹点位于重力观测值对应的等值线上;
2) INS存在积累误差,在用于匹配的观测序列的初始段,实际航迹点与INS提供的推算航迹点间存在偏差(Δx,Δy);
3) 匹配序列长度一般较短,在此期间,INS存在积累误差,但主要表现为前期的积累误差,匹配序列测量期间的积累误差因为时间短可以不予考虑。
若能够获得INS推算航迹相对实际航迹的平移量(Δx,Δy)和旋转角θ,则可获得INS航迹与实际航迹的平移关系T以及旋转关系R(θ)。 匹配定位过程如下所示。
1) 根据INS提供的推算点Pi(x,y),在其附近寻找重力观测值Ti在背景场上对应的等值线。
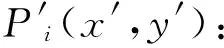
(1)
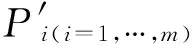
(2)
然后,计算旋转矩阵R(θ):
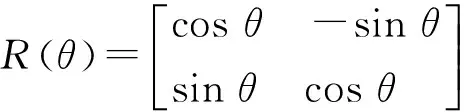
(3)

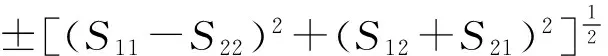
(S11+S22-λm)q0+(S21-S12)q3=0
q0=cos(θ/2),q3=sin(θ/2)
则旋转角θ为:
tan(θ/2)=(S11+S22-λm)/(S21-S12)
其中,λm是W矩阵4个特征值λ中的最大者。

(4)
4) 用确定的旋转矩阵R(θ)和平移量T,对P序列进行旋转变换,得到一组序列X:
X=R(θ)P-T
(5)
将X作为新的序列,重复步骤2)~4),直到相邻两次得到的对应点的点位差满足一定的限差条件,停止迭代,即迭代收敛。
5) 此时X序列中各点在背景场中的位置即为实际航迹点的或然位置。
5 仿真实验
本文选择的重力异常区域为北纬20°~30° ,东经125°~135° ,重力异常分辨率为2′×2′。仿真计算得出的航迹如图2所示,经向匹配误差图如图3所示,纬向匹配误差图如图4所示。
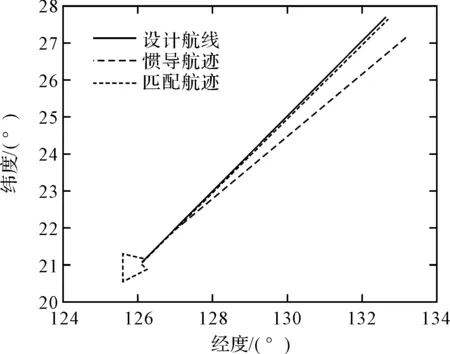
图2 航迹图

图3 经向匹配误差
从仿真的结果可以看出,惯性导航的误差随时间的增加而逐渐增大,经过重力异常数据匹配修正之后可以大大减小导航误差,总体上能够达到较高的导航精度。匹配精度和重力异常变化有关。经分析可知,此算法在重力异常变化较明显的区域可以达到较高的导航精度,在重力异常变化不明显的区域则精度较差,需要利用其它的导航信息加以补充,在重力异常变化较小的区域还会出现匹配误差跳变情况使辅助导航失败。因此在采用重力异常进行辅助导航时需要精心规划导航路线,防止辅助导航出现匹配失败。
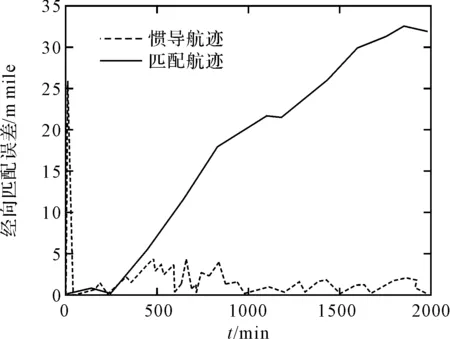
图4 纬向匹配误差
6 结语
根据以上计算分析可知,基于重力背景场,借助ICCP技术,通过选择合适的航行路线,完全可以实现准确的重力匹配,并修正INS,实现水下载体的自主导航。利用重力场匹配技术进行水下辅助导航时,在重力测量精度很高且重力异常变化较明显的情况下,可以取得较高的匹配精度,但重力测量精度不够且重力异常变化较小的情况下,实际应用效果较差。
[1] Rice H, Mendelsohn L, Aarons R, et al. Next Generation Marine precision Navigation system[C]// Position Location and Navigation symposium, San Diego, 2000.
[2] Affleck CA, Jircitano A. Passive Gravity Gradiometer Navigation system [C]// Position Location and Navigation Symposium, Las Vegas, 1990.
[3] Marshal M R, Richard EH, Christopher MS. An Investigation Into the Feasibility of Using a Modern Gravity Gradiometer Instrument of Passive Aircraft Navigation and Terrain Avoidance [C]// The 2009 International Technical Meeting of The Institute of Navigation, Anaheim, 2009.
[4] Behzad KP, Behrooz KP. Vehicle Localization on Gravity Maps[C]// SPIE—The International Society for Optical Engineering, Orlando,1999.
[5] 刘承香. 水下潜器的地形匹配辅助定位技术研究[D].哈尔滨: 哈尔滨工程大学, 2003.
[6] Bishop C. Gravitational Field Maps and Navigational Erors[J]. IEEE Journal of Oceanic Engineering, 2002, 27(3):726-737.
[7] 张红梅,赵建虎,王爱学等.预平移简化ICCP匹配算法研究[J]. 武汉大学学报·信息科学版, 2010, 35(2):1432-1435.
[8] 赵建虎,张红梅,王爱学等.利用ICCP的水下地磁匹配导航算法[J].武汉大学学报·信息科学版,2010,35(3):261-264.
[9] Wang Zhigang, Bian shaofeng. A Local Geopotential Model for Implementation of Underwater Passive Navigation[J]. Progress in Natural Science, 2008, 18(9): 1139-1145.
[10] 吴太旗, 黄谟涛, 边少锋等. 直线段的重力场匹配水下导航新方法[J]. 中国惯性技术学报, 2007,15(2):202-205.
[11] Xiao Shenghong, Bian Shaofeng. Research on Regional Model of Continuous Fourier Series of Marine Magnetic Anomaly Field Using for the Geomagnetic Navigation[C]// International Conference on Industrial and Information System, Wuhan, China, 2010.
Gravity Matching Simulation of Real-time ICCP Algorithm
CAI Longfei ZHENG Tong
The aided navigation with geophysical field is a new research direction in integrated navigation technology, and it provides a new method for the autonomous and passive navigation of underwater vehicle. As one of the important matching navigation algorithms, the Iterative Closest Contour Point (ICCP) algorithm has some disadvantages such as bad real-time performance, low searching speed. With respect to the two limitations mentioned above, the way to fix length of the sample sequence is adopted to improve the sampling structure, and a new iteraton equation with single sample point is derived. What's more, the searching mode of moving window is adopted to reduce the searching area and improve the operation speed of the algorithm. Finally, the real-time ICCP algorithm is designed. The simulation results show that the matching results can track the real positions in time.
ICCP, gravity matching, aided navigation, real-time
2016年6月6日,
2016年7月17日
蔡龙飞,男,工程师,研究方向:舰船电子。郑彤,女,博士,工程师,研究方向:舰船电子。
TP301
10.3969/j.issn.1672-9730.2016.12.025
