动态规划在测控装备效费分析中的应用*
2017-01-11何府强
何府强 王 垚
(91913部队 大连 116041)
动态规划在测控装备效费分析中的应用*
何府强 王 垚
(91913部队 大连 116041)
文章从动态规划的基本概念出发,并根据多阶段决策的性质特点,通过对问题进行合理的分析和假设,建立了装备最大效益的动态规划模型。运用反向递推算法求得其最优经费投入方案,从而最大化的发挥其军事效益。
动态规划;效益;决策;模型
(No. 91913 Troops of PLA, Dalian 116041)
Class Number E951
1 引言
测控装备是指具备遥测、外测、安控、光学跟踪等功能的装备,在靶场中主要担负导弹的弹道测量和安全控制等任务。随着靶场职能使命的拓展,测控装备将发挥越来越重要的作用,如何对测控装备进行科学化、制度化的管理,使其发挥最大的军事效益,是摆在装备管理人员面前的一个非常重要的问题。优化问题,一般是指用“最好”的方式,使用或分配有限的资源,即劳动力、原材料、机器、资金等,使得费用最小或者利润最大,最优化模型就是根据优化问题的具体情况建立的数学模型。由于装备的效益与投入的费用息息相关,那么关键的问题便是投入一定的装备经费后,如何对其进行有效的分配,才能发挥出装备的最大效益,文章运用动态规划的方法建立测控装备的效费模型[1],提出经费分配方案,从而最大化地发挥出其军事价值。
2 动态规划的基本概念
动态规划是20世纪50年代前后由美国数学家贝尔曼等建立和发展起来的一种解决多阶段决策问题的优化方法[2],主要包括以下几个方面的要素:
1) 阶段(Stage)
求解多阶段决策问题必须把所给问题的过程,恰当地划分为若干个相互联系的阶段,以便于求解。通常用k表示阶段变量,k=1,2,…,n。n表示阶段总数。
2) 状态(State)
状态就是某一阶段的出发位置,同时它又是前一阶段的结束位置。用状态变量Sk表示第k阶段所有状态的集合,sk表示第k阶段的某个状态,式(1)表示第k阶段有r个状态。
Xk={sk(1),sk(2),…,sk(r)}
(1)
3) 决策(Decision)
决策就是某阶段的状态给定以后,从该状态演变到下一状态的选择。描述决策的变量称为决策变量。常用xk(sk)表示第k阶段处于状态sk时的决策,用Dk(sk)表示第k阶段处于状态sk时的允许决策集合,显然有xk(sk)∈Dk(sk)。
4) 策略(Policy)
由过程的第一阶段开始到终点为止的整个过程,称为问题的全过程。式(2)表示由每段的决策xi(si)(i=1,2,…,n)组成的决策序列就称为全过程策略(简称策略),记为p1,n。
p1,n={x1(s1),x2(s2),…,xn(sn)}
(2)
由第k阶段到终点的过程称为原过程的后部子过程(或称为k子过程),其决策序列{xk(sk),xk+1(sk+1),…,xn(sn)}称为k子过程策略,如式(3)所示:
pk,n={xk(sk),xk+1(sk+1),…,xn(sn)}
(3)
用P表示所有允许策略的集合,从中找出的效果最好的策略称为最优策略。
5) 状态转移方程
只要sk及xk一经确定,第k+1阶段的状态变量sk+1的值就完全确定,写成关系式为:sk+1=Tk(sk,xk),这个式子称为状态转移方程,表示第k阶段到第k+1阶段状态的转移规律。
6) 指标函数
指标函数是一个定义在全过程策略和所有后部子过程策略上的数量函数,是评价一个策略效果的数量指标,用Vk,n表示如式(4)所示[3]:
Vk,n=Vk,n(sk,pk,n(sk))
=Vk,n(sk,xk,sk+1,…,sn+1) (k=1,2,…,n)
(4)
用fk(sk)表示Vk,n的最优值。
3 模型的建立
测控装备的效费分析实际上是一个单目标多阶段决策问题,首先决策者根据投入经费的多少计算出测控装备的效费模型,即效益—费用模型,然后将各型装备效益值进行累加,将效益总和作为目标函数,最后将总的装备经费对各型装备进行分配,在各型装备满足其最低效益的前提下,计算出其最优解,为决策者提供最优的决策,从而得到最大的军事效益[4]。
根据测控装备的实际服役情况,其效益值与装备的初始效益值、测控装备允许达到的最大效益值、效益增长系数以及投入的经费等因素有关,一般可用式(5)表示[5]:
(5)
其中:N(x)为投入经费后的装备效益,N0为投入经费之前的装备效益值,Nm为测控装备允许达到的最大效益值,r0为效益值较低时的增长系数,x为投入的经费。
以上建立的阻滞增长模型—Logistic模型,考虑了效益值与投资经费之间的关系,比较符合装备在实际应用中的数学规律,可用于对测控装备效益的计算。
测控装备的效益值是属于多阶段决策问题,由于在靶场应用中有多型装备,如遥测、雷测、光测等,作为装备管理人员,考虑该问题的决策过程实际上是一种在多个相互联系的阶段分别做出决策以形成决策序列的过程,而这些决策都是根据总体最优化这一共同的目标而采取的。对测控装备进行效益分析时,决策者能够根据总的经费投入情况,对经费进行科学高效的分配,合理地确立每一阶段的经费投入情况,最终达到装备的最大效益值[6]。
动态规划的最优化原理为:“作为整个过程的最优策略具有这样的性质:即无论过去的状态和决策如何,对前面的决策所形成的状态而言,余下的诸决策必须是最优策略。”根据这个原理,可以把多阶段决策问题的求解过程看成是对若干个相互联系的子问题逐个求解的反向递推过程[7]。
一般地,一维效益模型问题可归结为:有n型装备,总的经费为a,每型装备的经费投入为xk,带来的装备效益为Nk(xk)。问如何分配经费,使总的总效益最大。
此问题可写成如下规划问题,如式(6)所示[8]:
(6)
用动态规划方法处理这类问题时,通常以把分配给某型装备的经费的过程作为一个阶段,把规划问题中的变量取为决策变量,将累计的量或随递推过程变化的量作为状态变量。
除此之外,在研究装备的最大效益值时,不单要考虑总的效益情况,也要考虑各型装备的最小效益值,这是因为在实际应用中,每型装备具有不可或缺性,不能因为其效益小或者效益增长速度慢而对其减少经费投入或者不投入经费[9]。
下面用动态规划的方法求解,为此建立它的动态规划模型。
设阶段变量:以n型装备来划分阶段,有k=1,2,…,n;
决策变量xk,表示分配给第k阶段(即第k型装备)的经费;
状态变量sk,表示分配给第k至第n型装备的经费;
状态转移方程,如式(7)所示:
sk+1=sk-xk
(7)
允许决策集合,如式(8)所示:
Dk(xk)={xk|0≤xk≤sk}
(8)
阶段指标函数vk(xk),表示投入经费xk时得到的效益值,如式(9)所示:
(9)
最优指标函数fk(sk),表示投入经费sk时分配给第k至第n型装备,在各种决策方案下获得的最大军事效益,如式(10)所示:
(10)
基于这种分析,根据动态规划最优化原理,结合式(5)的装备效益模型,建立装备效益的动态规划模型如下,如式(11)所示:
(11)
其中,Nmi为第i型测控装备允许达到的最大效益值,N0i为投入经费之前第i型装备效益值,r0i为第i型装备效益值较低时的增长系数,ci表示第i型装备的最小效益值(i=1,2,3,…,n)。
4 模型的应用
假设某靶场有遥测、外测、脉冲雷达和光测四种型号的测控装备,各型装备的参数Nmi、N0i、r0i和ci如表1所示,总的经费为100万元。

表1 各型测控装备的参数值
根据表1参数值,假设遥测、外测、脉冲雷达和光测四种型号的测控装备分别表示四个阶段,则建立动态规划模型如下,如式(12)所示:
(12)
根据动态规划的基本思想,可以把经费分配的过程看成是对若干个相互联系的子问题,然后逐个求解的反向递推过程。
具体解决方法如下:
根据各型测控装备的参数值,得出各阶段的指标函数为[10]
v1(x1)=N1(x1)=0.95/(1+0.19×e-0.02x1)
v2(x2)=N2(x2)=0.95/(1+0.22×e-0.03x2)
v3(x3)=N3(x3)=0.92/(1+0.13×e-0.02x3)
v4(x4)=N4(x4)=0.93/(1+0.33×e-0.03x4)
设s4=x4,s4+x3=s3,s3+x2=s2,s2+x1=s1=100,则有s4=x4,0≤x3≤s3,0≤x2≤s2,0≤x1≤s1=100。
通过编写Matlab程序,计算结果如下[11]:
第4阶段:
第3阶段:
=0.92/(1+0.13×e-0.02x3)
+0.93/(1+0.33×e-0.03s4)

同理可得,在第2阶段:
第1阶段:
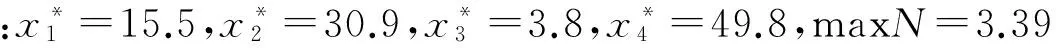
根据以上结果,当遥测、外测、脉冲雷达和光测四种测控装备的投入经费分别为15.5万元、30.9万元、3.8万元和49.8万元时,可以达到最大的效益值,最大效益值为3.39。
5 结语
动态规划是一个复杂而系统的过程,涉及到诸多因素和各因素之间的内部关系,动态规划就是为解决这一多阶段决策问题而产生的一种数学分析方法,其原理概括了动态规划方法的基本思想,把一个较复杂的问题,按照其阶段划分,分解成若干个较小的局部问题,然后根据局部问题的递推关系,依次做出一系列决策,直到整个问题达到总体最优的目标,从而为决策者提供最优的控制策略。
[1] 冯尚友.多目标决策理论方法与应用[M].武汉:华中理工大学出版社,1990.
[2] 姜启源.数学模型(第三版)[M].北京:高等教育出版社,2003.
[3] 边馥萍,侯文华, 梁冯珍.数学模型方法与算法[M].北京:高等教育出版社,2005,163-168.
[4] 陈廷. 多目标群决策方法及应用研究[D].北京:中国人民解放军信息工程大学,2005.
[5] 华东师范大学数学系编.《数学分析》[M].北京:人民教育出版社,1980:149.
[6] 陈守煜,模糊优选理论与模型[J].控制与决策,1993,8(1):25-29.
[7] 厉洋峰. 动态规划及其在数学模型中的应用[J]. 中国新技术新产品,2009,16:244-245.
[8] 陈开周. 最优化计算方法[M].西安:西安电子科技大学出版社,1985.
[9] 赵登虎. 定量分析在军事决策中的作用[J]. 南京政治学院学报,2009,06:87-89.
[10] 蒲俊,吉家锋,伊良忠.MATLAB6.0数学手册.(2002年1月第一版)[M].上海:浦东电子出版社,2002:95.
[11] 刘卫国.MATLAB 程序设计与应用[M].北京:高等教育出版社,2006.
Application of Dynamic Programming in the Cost Effectiveness Analysis of Measurement and Control Equipment
HE Fuqiang WANG Yao
This paper started from the basic concept of dynamic programming, according to the characteristics of the multi stage decision, and then established the dynamic programming model for the maximum benefit of equipment through rational analysis and hypothesis. By using the backward recursive algorithm, the optimal investment scheme was obtained, which can maximize its military effectiveness.
dynamic programming, benefit, decision, model
2016年6月10日,
2016年7月28日
何府强,男,助理工程师,研究方向:装备管理工程。王垚,男,工程师,研究方向:装备管理工程。
E951
10.3969/j.issn.1672-9730.2016.12.031
