EGM2008和加权整体最小二乘在GPS高程拟合中的应用
2017-01-10范昆飞易桂轩孔建刘立
范昆飞,易桂轩,孔建,刘立
(1.南宁市国土测绘地理信息中心,广西 南宁 530021; 2.武汉市测绘研究院,湖北 武汉 430000;3.武汉大学,湖北 武汉 430079; 4.浙江省第一测绘院,浙江 杭州 310012)
EGM2008和加权整体最小二乘在GPS高程拟合中的应用
范昆飞1*,易桂轩2,孔建3,刘立4
(1.南宁市国土测绘地理信息中心,广西 南宁 530021; 2.武汉市测绘研究院,湖北 武汉 430000;3.武汉大学,湖北 武汉 430079; 4.浙江省第一测绘院,浙江 杭州 310012)
在利用地球重力场模型EGM2008结合GPS/水准数据计算得到剩余高程异常的基础上,利用加权整体最小二乘(WTLS)方法对剩余高程异常进行三次曲面拟合,获得更加精确的GPS高程拟合模型。通过对CORS系统GPS/水准数据的拟合和外部精度检核表明,综合EGM2008和WTLS方法能够显著提高GPS高程异常拟合精度。
EGM2008;WTLS;高程异常;三次多项式
1 引 言
GPS观测技术具有高效性、全球性、高精度等优点,在道路交通、工程建设等诸多领域获得了广泛应用,尤其在测绘领域引起了革命性的变化。传统水准测量获得高程的方法费时费力,且容易受到观测环境的影响。GPS测量轻便、高效,观测点之间相互独立,没有误差积累,相对于传统水准测量有很大优势。但是GPS观测获得大地高为相对于地球椭球的几何高程,需要将其转换为正常高[1,2]。最常用的高程拟合方法为将高程异常描述为曲面函数,利用GPS/水准点的高程异常数据和平面坐标,采用最小二乘方法进行曲面函数系数求解[3~5]。但是传统最小二乘方法只对观测值进行改正,当观测向量和系数矩阵由于函数模型、仪器误差等影响含有误差时,最后求解结果是有偏的。加权整体最小二乘(Weighted Total Least Squares)以观测值和系数矩阵残差平方和最小为准则,同时对观测向量和系数矩阵进行改进,能够改正函数模型存在误差的问题。同时通过迭代的方法确定观测向量和系数矩阵的权,有效解决了GPS观测数据和水准数据精度等级不同的问题[6~9]。
国际上先后实施了CHAMP、GRACE、 GOCE卫星重力计划。高精度、高时空分辨率的卫星重力数据极大地完善了地球重力场数据。美国国家地理空间情报局(NGA)综合利用卫星重力数据、地面重力数据、数字地面模型等,研制新一代超高阶地球重力场模型EGM2008。利用高精度地球重力场模型能够精确计算重力场短波分量,弥补GPS水准拟合在反映地形起伏方面的不足。综合利用加权整体最小二乘和EGM2008,对实际GPS/水准数据进行区域似大地水准面拟合,拟合结果精度表明该方法能够有效提高GPS高程精度。
2 GPS高程拟合与加权整体最小二乘
2.1 三次曲面函数
在对区域GPS高程进行拟合时,通常采用二次多项式函数对GPS点的高程异常ζ与平面坐标(x,y)进行描述,具体函数关系为
(1)
而文献[10]研究表明,三次多项式曲面函数在GPS高程拟合中精度更高。在现有计算机计算能力条件下,二次多项式和三次多项式计算耗费时间都十分微小,因此本文采用三次多项式对GPS高程进行拟合,具体函数表达式为:

(2)
设在该区域内有n个GPS水准点,则曲面函数的矩阵形式为:
l=Aβ
(3)
其中l为高程异常ζ观测向量,A为GPS/水准点的平面坐标(xi,yi)组成的设计矩阵,β为三次多项式待求系数。
矩阵的具体形式为:
(4)
2.2 加权整体最小二乘(WTLS)
由于观测方程中,观测向量l和设计矩阵A中的误差不可避免,因此引入EIV模型[11]:
l-ε=(A-σ)β
(5)
其中l为含有随机误差ε的高程异常观测向量;A为含有随机误差σ的设计矩阵;β为三次多项式待求系数。加权整体最小二乘计算中,设计矩阵A的权阵为:
QA=Q0⊗Qx
(6)

WTLS的迭代步骤为:
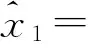
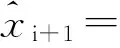
3 EGM2008地球重力场模型
美国空间情报局2009年发布了超高阶地球重力场模型EGM2008,该模型阶次达到了 2 159阶,空间分辨率约为5′×5′。由地球重力场模型EGM2008可以计算地球上任意一点的模型高程异常:

(7)

利用已知GPS/水准点数据可以计算得到水准高程异常ζ,EGM2008可以计算得到GPS/水准点的模型高程异常ζG,则剩余高程异常
ζres=ζ-ζG
(8)
通过三次曲面函数采用加权整体最小二乘方法对剩余高程异常ζres进行拟合,得到区域剩余高程异常模型,与EGM2008计算得到的模型高程异常ζG结合,最终获得该区域高程异常模型。
4 实例分析
本文选取某市CORS站点数据对综合加权整体最小二乘和EGM2008方法的有效性和精度进行验证。通过后期增加水准联测工作,该区域内联测水准的GPS控制点共25个,经过平面坐标标准化处理后,分布情况如图1所示。为检核上述方法的精度,选取其中9个点作为外部检核点(黑色三角),利用剩余16个点(空心圆圈)进行GPS高程拟合。从图1可以看出,该区域的GPS/水准点分布较为均匀,检核点主要分布在区域内部,不会因为检核点位置影响所得高程异常拟合模型检核精度。
为了检验加权整体最小二乘对设计矩阵A含有误差时的有效性,在拟合点中,D11和D24平面坐标加入了粗差,具体坐标和高程异常值如表1所示。
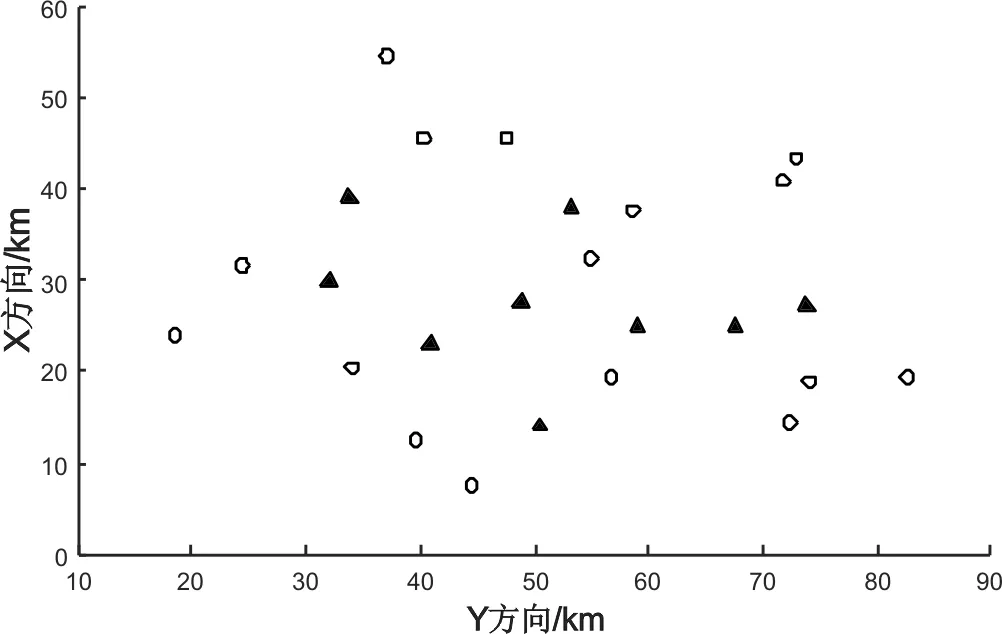
图1 GPS/水准点分布

含有粗差的GPS/水准数据 表1
分别利用传统LS方法、WTLS、EGM2008+WTLS三种方法对16个GPS/水准点进行高程拟合,得到该区域的高程异常模型,然后将9个检核点平面坐标带入各自模型进行模型精度检验。表2给出了三种拟合方法所得的三次多项式拟合参数。

曲面拟合参数 表2
图2和图3分别给出了LS和WTLS方法GPS高程拟合结果的三维视图,图中标出了粗差点D11和D24的位置。从图中可以看出,D11由于加入了人为粗差,位置偏离到了边缘位置,而该位置周围点的高程异常值都非常小。从图2与图3对比中可以看出,在利用LS方法进行GPS高程拟合时,由于粗差点D11的存在,该区域的高程异常被明显向上拉升而偏离了周围GPS/水准点的高程异常值,导致了拟合结果与实际情况有较大偏差。粗差点D24同样导致了拟合结果的偏差。而WTLS方法综合考虑了GPS/水准点的高程异常和平面坐标的误差,对GPS/水准点进行迭代定权,消除了粗差对拟合结果的影响,建立了更加合理的拟合模型。从图3中可以看出,粗差点D11和D24并没有影响周围高程异常的拟合结果,并且其他部分的高程异常也更加贴合实际高程异常值。
图4给出了EGM2008+WTLS的GPS高程拟合结果的三维视图,从图中可以看出,与WTLS拟合结果相比,EGM2008+WTLS也没有受到粗差点的影响,并且由于EGM2008为检核点提供了更加精确的模型高程异常,使得拟合模型更加符合区域地形情况。其中区域中部起伏更加明显,整体趋势与检核点更加贴合。
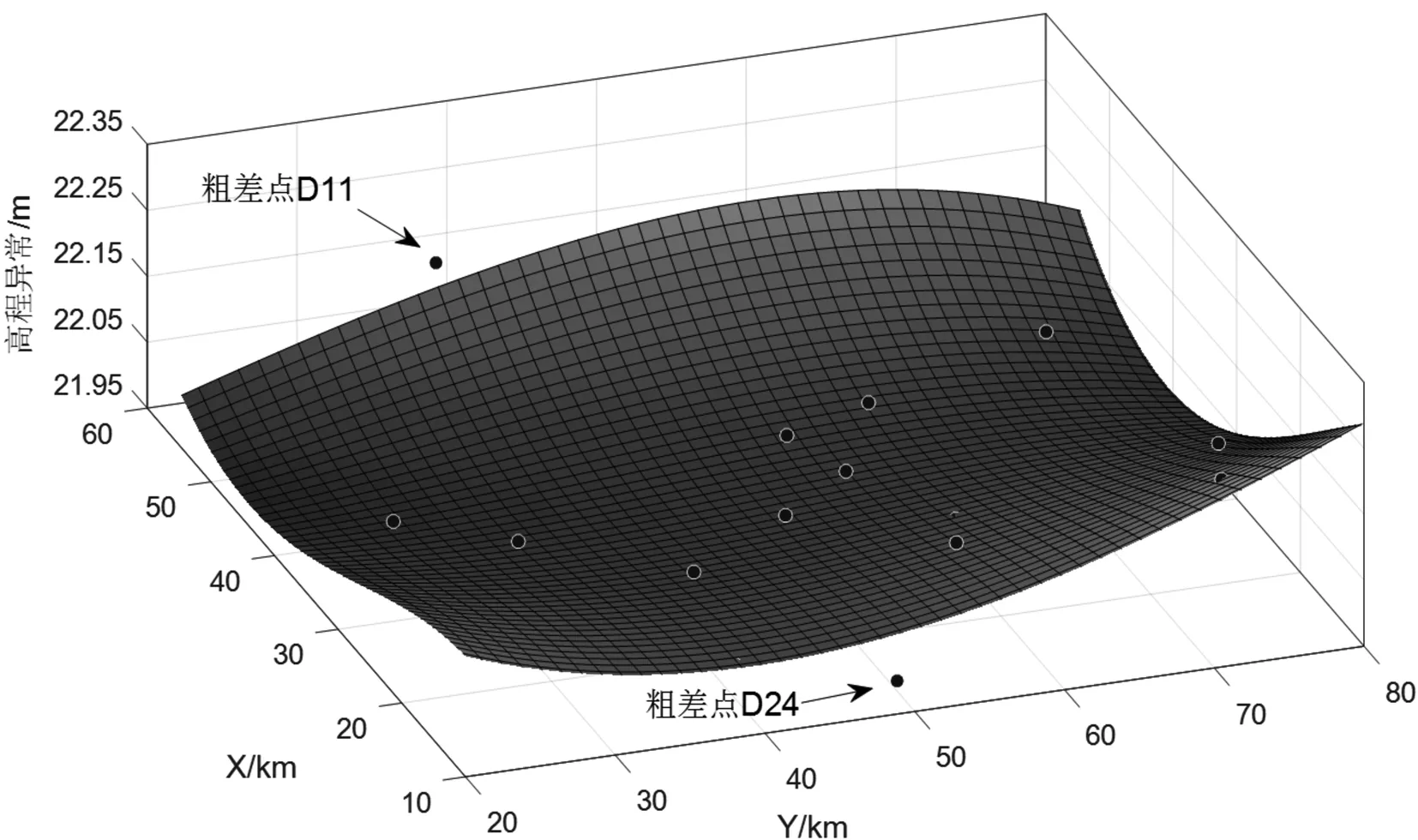
图2 LS方法GPS高程异常拟合结果
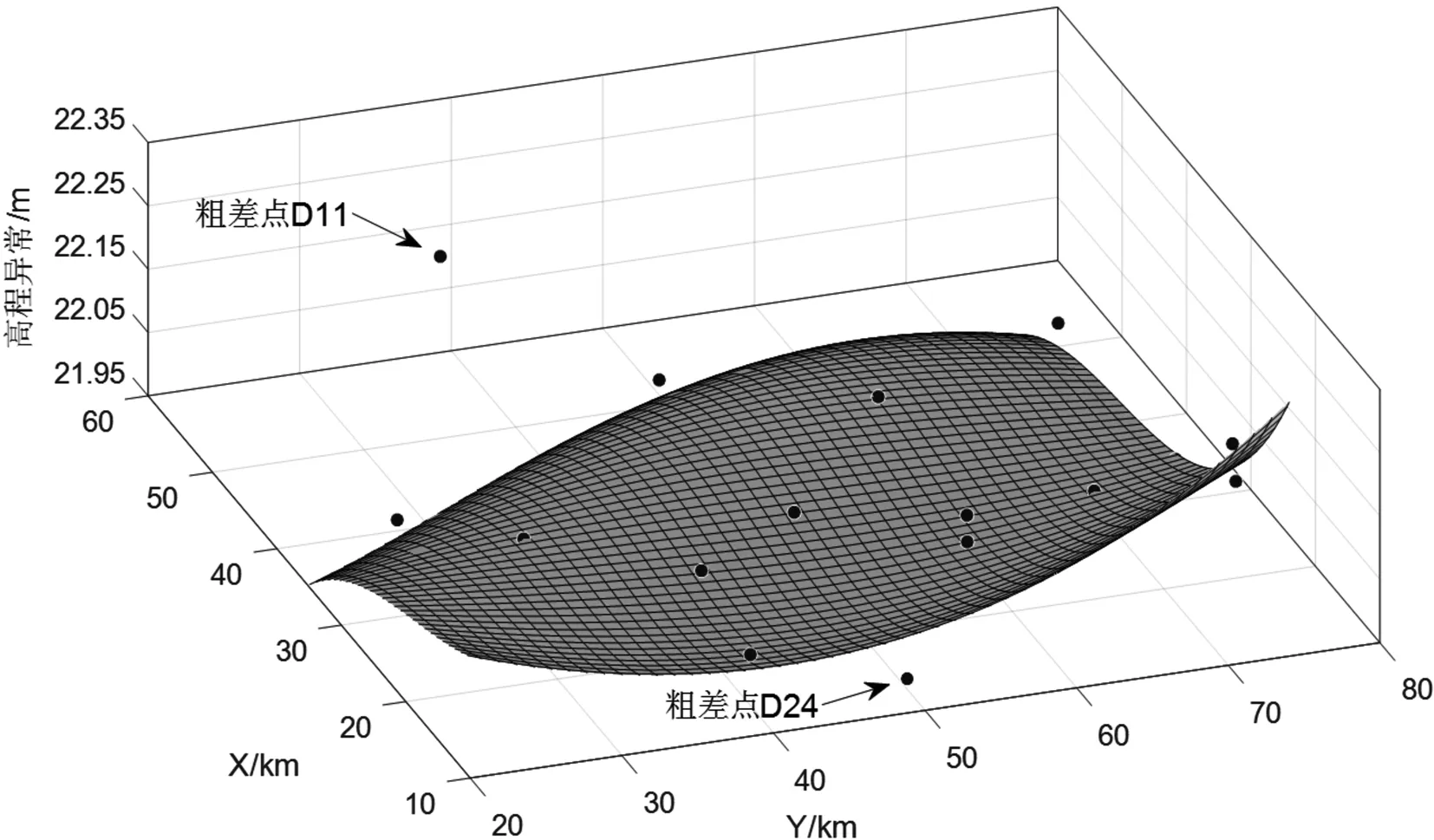
图3 WTLS方法GPS高程异常拟合结果

图4 WTLS+EGM2008方法GPS高程异常拟合结果

精度统计 表3
利用LS、WTLS、EGM2008+WTLS方法得到区域高程异常模型后,将9个检核点的平面坐标带入模型,获得这些点的拟合高程异常,与已知的水准高程异常做差得到模型的拟合误差。表3给出了模型拟合的精度统计结果。从表3中可以看出,LS方法的拟合误差较大,最大值为 0.060 1 m,最小值为 0.027 3 m,检核点中误差为 0.048 3 m;WTLS拟合精度相对于LS方法有较大提高,EGM2008+WTLS拟合精度最高,其中检核点误差最大值为 0.047 1 m,最小值为 0.005 4 m,中误差为 0.025 3 m。
5 结 论
传统最小二乘方法(LS)只考虑了观测向量中的误差,当设计矩阵A中含有误差时,所得结果通常是与实际情况有较大偏差的。整体最小二乘虽然考虑了设计矩阵中的误差,但是将其与观测向量误差等精度处理,忽略了两种数据的不等精度的现实。本文首先采用新一代的超高阶地球重力场模型,计算区域模型高程异常,获得剩余高程异常后,利用加权整体最小二乘方法,通过引入EIV模型,并迭代计算各个GPS/水准点数据的权,获得更加合理的拟合模型。实际高精度CORS系统GPS/水准数据拟合结果的外部检核精度表明,EGM2008+WTLS方法GPS高程拟合模型精度优于LS和WTLS方法。
[1] 魏子卿,王刚. 用地球位模型和GPS/水准数据确定我国大陆似大地水准面[J]. 测绘学报,2003,32(1):1~5.
[2] 高原,张恒璟,赵春江. 多项式曲面模型在GPS高程拟合中的应用[J]. 测绘科学,2011,36(3):179~181.
[3] 王解先. 工业测量中一种二次曲面的拟合方法[J]. 武汉大学学报·信息科学版,2007,32(1):47~50.
[4] 吴良才,胡振琪. GPS高程转换方法和正常高计算[J]. 测绘学院学报,2004,21(4):256~258.
[5] 高伟,徐绍铨. GPS高程分区拟合转换正常高的研究[J]. 武汉大学学报·信息科学版,2004,29(10):908~911.
[6] 赵辉,张书毕,张秋昭. 基于加权总体最小二乘法的GPS高程拟合[J]. 大地测量与地球动力学,2011(5):88~91.
[7] VAN HUFFEL S,VANDEWALLE.The Total Least Squares and Least Squares Techniq ues in the Presence of Errors on all Data[J]. SIAM Journal on Numerical Anal-ysis,1991,25(5):765~769.
[8] SCHAFFRIN B,ANDREAS W.On Weighted Total Least squares Adjustment for Linear Regression[J].Journal of Geodesy,2008,82(7):415~421.
[9] Felus Y A,Schaffrin B.Performinng Similarity Transformations Using the Error-in-variables Model[C]. ASPRS 2005 Annual Conference Baltimore,Maryland,2005.
[10] 丁海勇,孙景领. GPS高程转换的总体最小二乘方法研究[J]. 大地测量与地球动力学,2013,33(3):52~55.
[11] GOLUB G H,VAN LOAN CH.An Analysis of the Total Least Squares Problem [J]. SIAMJournalonNu-merical Analysis,1980,17(6):883~893.
[12] 陈俊勇,对SRTM3和GTOPO30地形数据质量的评估[J]. 武汉大学学报·信息科学版2005,30(11):941~942.
[13] Ågren J. Evaluation of EGM2008 and PGM2007A over Sweden[J]. Newton’s Bull,2009,4:99~109.
[14] 张兴福,刘成. 综合EGM2008模型和SRTM/DTM2006.0剩余地形模型的GPS高程转换方法[J]. 测绘学报,2012,41(1):25~32.
Application of Integrated EGM2008 and Weighted Total Least Squares in GPS Height Fitting
Fan Kunfei1,Yi Guixuan2,Kong Jian3,Liu Li4
(1.Nanning Land Surveying and Mapping Geographic Information Center,Nanning 530021,China;2.Wuhan Geomatics Institute,Wuhan 430000,China;3.Wuhan University,Wuhan 430079,China;4.The first surveying and Mapping Institute of Zhejiang Province,Hangzhou 310012,China)
Based on the calculation of the residual height anomaly by using the earth gravity model EGM2008 and GPS/ leveling data,the weighted total least squares(WTLS)method is employed to carry out the three curve fitting of the residual height anomaly and obtain more accurate GPS height fitting model. The fitting of the CORS network GPS/ level data and the external precision test show that,comprehensive EGM2008 and WTLS methods can significantly improve the accuracy of GPS height anomaly fitting.
EGM2008;WTLS;height anomaly;three degree polynomial
1672-8262(2016)06-88-05
P228
A
2016—09—02
范昆飞(1986—),男,工程师,主要研究方向为CORS维护与应用。
南宁市第三批特聘专家科研项目;南宁市人才小高地资助项目。 获奖项目:本论文的研究工作获得中国地理信息产业协会地理信息科技进步奖二等奖。
