非完全信息环境中一种基于隐马尔科夫的博弈式功率控制机制

朱 江,张玉平

(重庆邮电大学重庆市移动通信重点实验室,重庆400065)

非完全信息环境中一种基于隐马尔科夫的博弈式功率控制机制

朱 江,张玉平

(重庆邮电大学重庆市移动通信重点实验室,重庆400065)

针对非完全信息环境下认知无线网络中的分布式功率控制问题,根据不同非授权用户对信道检测结果的差异,以及信道检测结果的非独立性,提出了一种基于隐马尔科夫模型的功率博弈机制.非授权用户可利用该模型推测其它非授权用户是否参与博弈,从而提升了博弈的信息准确度,使得非授权用户能够选择更优的发射功率.仿真表明,该功率控制机制在保证通信质量的前提下能够获得更大的容量功率比,具有更好的功率效率.

非完全信息;隐马尔科夫;博弈式功率控制

1 引言

认知无线电被认为是一种能有效解决频谱资源缺乏问题的关键技术.在认知无线网络中,当节点以竞争的方式使用频谱资源时,需要有效的机制来协调它们的行为(如发射功率、信道选择等),使资源得到有效利用,并满足用户的业务需求[1].其中功率控制机制由于能够有效避免干扰,提高能量效率,是认知无线网络研究的重点和热点[1～7].

博弈中的信息对博弈结果有决定性的影响[8,9].现有大多数文献[4～7]在设计博弈式功率控制机制时,都是理想化地假设参与博弈的网络实体所获取环境信息同质,没有考虑用户信息的非完全性.而所谓信息的非完全性是指由于用户所处环境差异和认知能力差异,即使对同一环境对象,不同用户在同一时间段的认知结果也可能不同,因此用户能准确知道自己的结果,但对其它用户的结果只能通过推测获得.为更贴近网络的实际情况,本文考虑了环境信息的非完全性,根据不同用户对信道检测结果的差异,以及信道检测结果的非独立性,提出了一种基于隐马尔科夫模型(Hidden Markov Model,简称HMM)[10]的博弈式功率控制机制.借助该模型,非授权用户可获得更准确的关于竞争对手的信道检测结果,更真实地确定竞争对手集合,从而提升用户和系统的能效.

2 系统模型

考虑一个CDMA制式的中心辐射式网络[11],该网络的某一小区内有若干授权用户和N个非授权用户.小区内存在两个基站分别为授权用户和非授权用户收发数据.将授权用户的网络建模为分时隙系统(Slotted System),频域信道是否被授权用户占用满足两状态马尔科夫链,信道状态在相邻两个时隙内以概率pij进行转移[12].非授权用户在检测到授权用户未占用信道时利用信道传输数据.将信道状态记为0、1两种状态,且在一个时隙内信道的状态不会改变.信道状态为1表示授权用户未占用信道,此时非授权用户可以利用信道传输数据,而状态为0则表示信道已被授权用户占用,非授权用户不能利用信道传输数据.由于各个非授权用户独自检测信道状态,导致非授权用户对信道状态的判决结果存在差异.

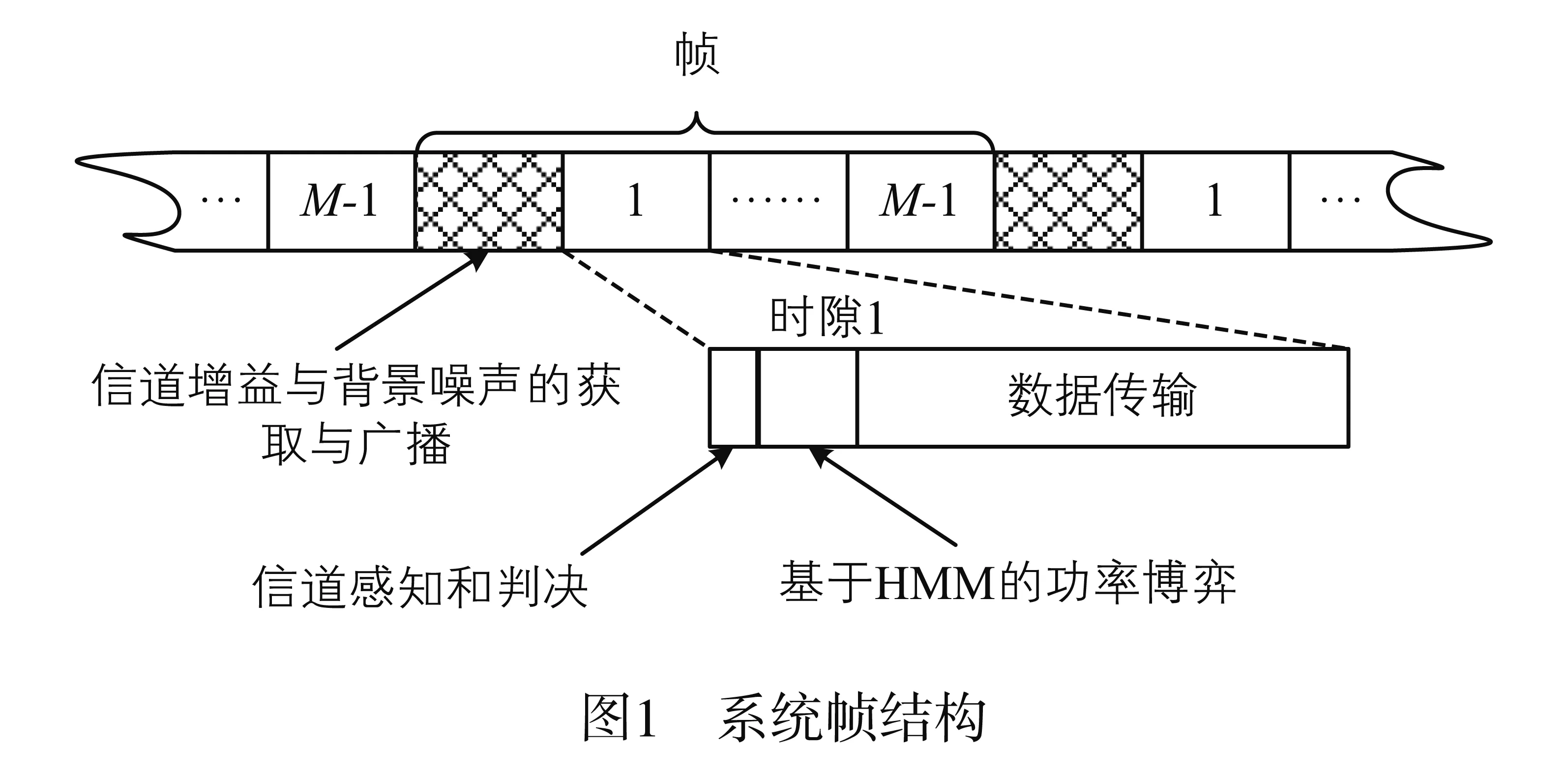
系统帧结构如图1所示,每帧分为若干时隙.考虑到分时隙系统中信道在0、1两种状态频繁转变,且反馈开销过大,本文采用基于信道增益估计的每时隙内无反馈博弈式功率控制机制[13],在时隙内的某特定时间段内通过迭代运算求出博弈的均衡值.如图1所示,各帧中第一个时隙0用于估计每个非授权用户到基站的信道增益和背景噪声,并将这些信息由基站广播给非授权用户.通过带外控制信道的信标收发来估计信道增益[14],为了确保带外控制信道的可靠性,使用一个授权信道作为带外控制信道[15].假设非授权用户的移动速度较慢,则一帧时间内信道增益不变.从第1时隙开始,各帧的第一部分用于感知信道是否被授权系统占用.若没有被占用,则进行基于HMM的博弈式功率控制实现分布式功率调整.接下来完成数据传输.

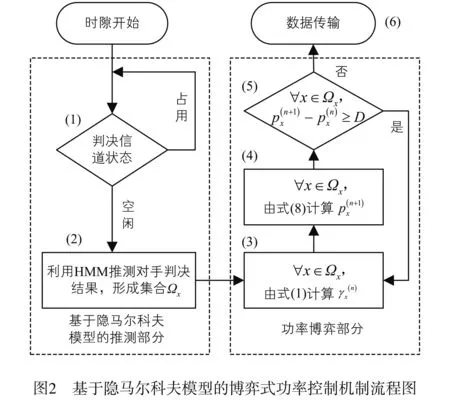
设非授权用户x的扩频带宽为W;发射功率为px;非授权用户的信道增益为hx;R为信息传输速率;基站处的背景噪声功率为N0.则非授权用户x在基站处的信干比定义为[16]:

(1)

其中,G=W/R为扩频处理增益,且Ix为非授权用户x在基站处受到的干扰,可由下式求得:

(2)

3 非合作博弈式功率控制

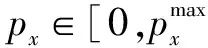
Ux(px,p-x)=e-θ(γx-γ0)+λpxhx

(3)

(3)式中,θ为满意度系数;γ0为非授权用户的目标信干比,非授权用户保证通信质量的目标为γx≥γ0;价格系数λ是非授权用户发射单位功率所付出的代价.e-θ(γx-γ0)表示非授权用户在信干比达到γx后继续增加信干比的需求程度.λpxhx表示非授权用户与基站通信所付出的发射功率代价.可见,用户不是追求最大化信干比,而是寻求信干比和发射功率之间的平衡,在获得接近γ0的信干比条件下,降低发射功率.由于非授权用户都是自私的,因此在选择策略时要最小化代价.因此将优化模型表示为:

(4)

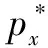
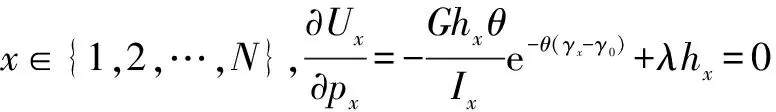
(5)

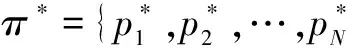
0<λIx≤Gθ

(6)

将式(1)代入式(5)可得到解方程组的表达式为:

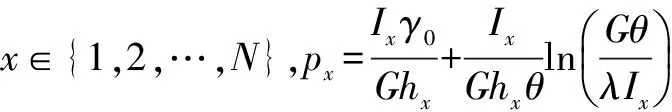
(7)

本文借用定点(Fixed Point)迭代法求解N个用户博弈的纳什均衡π*的近似解,该算法已被证明能够收敛.非授权用户x进行本地迭代运算,每一步迭代公式为:∀x∈{1,2,…,N},

(8)

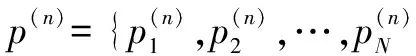
定理1 本文中的非合作博弈模型存在纳什均衡解,且纳什均衡解具有唯一性.

证明:非合作博弈存在纳什均衡解时需满足以下两个条件:

(1)非授权用户x的策略空间Px是欧几里德空间中非空的、闭的、有界的凸集;

(2)非授权用户x的代价函数Ux(px,p-x)在px上连续,且在px上是拟凹函数.

(9)

因此Ux(px,p-x)在px上是凹函数,也即Ux(px,p-x)是拟凹的.条件(1)、(2)都得以满足,所以非合作博弈式功率控制存在纳什均衡.

记由Ux(px,p-x)求得的最优功率p=R(p)为对应反应函数.由一个标准函数收敛到唯一点可知,要证明纳什均衡的唯一性,只需证明p=R(p)满足标准函数的3个性质[20]:正性,即R(p)>0;单调性,即若p′≥p,则R(p′)≥R(p);可量测性,即若∀β>1,则βR(p)>R(βp).

下面根据上述3个性质依次对p=R(p)进行证明:

(1)当不等式(6)成立时,0<λIx≤Gθ,那么R(px)>0成立;

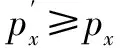
(10)

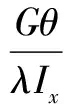
(3)设∀β>1,则有:

(11)

由于βIx-(β-1)N0>Ix,所以βR(px)>R(βpx)成立.

综上所述,R(p)满足标准函数的三个条件,因此非合作博弈式功率控制的纳什均衡解唯一.证毕

4 隐马尔科夫模型

由式(1)可知,非授权用户受到的干扰与同一小区内其它非授权用户的发射功率相关.因此,非授权用户检测到某信道可用后,要知道其它非授权用户中有哪些也有同样的判决结果,从而确定和自己形成真正竞争关系的非授权用户集合.然而在非完全信息环境下,非授权用户不能直接得到其它非授权用户的判决结果,只能依靠自己的判决结果对这些信息进行推测.

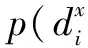
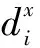
(12)

定义1 非授权用户x依据式(12)并由最大后验概率准则推测竞争对手判决结果的方法记为MAP方法.

定理2 实际系统中,非授权用户x和y同时检测信道,因其检测过程独立,它们之间的检测概率独立,则

(13)

证明:根据全概率公式有

(14)

若在同一时隙,非授权用户x和y检测信道,它们之间的检测概率独立,则上式可写成

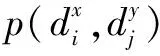
(15)

另一方面,则根据全概率公式有

(16)

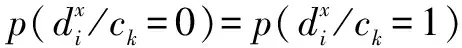
(17)

如果式(17)成立,从物理意义上讲意味着检测概率等于虚警概率,这种结果在实际系统中不存在,或者除非ck始终不发生变化.

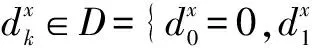
《欧盟排放交易指令》第11条明确规定，即使在2012年年底前未达成全球减排协议，欧盟各成员国的主管机构在2015年5月31日前应当继续受理关于项目级减排量（CERs/ERU）的申请。从指令措辞看，这个规定是针对欧盟各成员国的义务，具有强制性。根据欧盟交易指令，第一承诺期内产生的减排量可以在2015年5月31日前进行交易，这是没有疑义的。

证明:某一非授权用户在t个时隙内判决的信道状态序列O=o1o2…ot满足下式关系:

p(ot|ot-1,ot-2,…,o1)

=p(ct-1|ot-1,ot-2,…,o1)p(ct|ct-1,ct-2,…,c1)p(ot|ct)

(18)

式(18)根据贝叶斯公式可得:

(19)

因为信道状态序列ct,ct-1,…,c1为马尔科夫链,所以

p(ot|ot-1,ot-2,…,o1)=p(ct-1|ot-1)p(ct|ct-1)p(ot|ct) =p(ot|ot-1)

(20)

由式(20)可知非授权用户的判决状态序列满足马尔科夫性质.因此,非授权用户在t个时隙内对信道状态的判决序列是马尔科夫链.非授权用户在相邻两个时隙判决的信道状态的转移概率aij可由下式求得:

(21)

其中

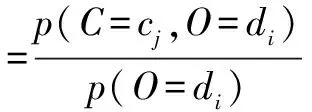
(22)

HMM可记为λ=(π,A,B),其中π={π0,π1}为非授权用户判决的信道状态的初始状态分布概率,A={aij}为每个非授权用户判决的信道状态的转移概率矩阵,其中aij=p(St=sj|St-1=si)(si,sj∈S)表示非授权用户在第t-1时隙判决的信道状态为si且在第t时隙判决的信道状态为sj的概率.B={bi(k)},(i,k=0,1)为条件概率,且bi(k)=P(O=dk|S=si)表示非授权用户推测某一竞争对手判决状态为si时其自身判决状态为dk的概率.如何用上述HMM中的观测状态序列推测出最优可能的隐藏状态序列是HMM的一个典型问题,可以用Viterbi算法等实现,此处不再赘述.

定义2 将非授权用户应用上述HMM推测竞争对手判决结果的方法记为HMM方法.

在HMM方法和MAP方法中,每个时隙的开始,若非授权用户x要参与博弈,且推测出某竞争对手的判决结果为1,则将其加入集合Ωx中,Ωx的初始值为{x},显然Ωx∈{1,2,…,N}.值得注意的是,由于用户的判决结果不一定相同,每时隙参与博弈的非授权用户数会变化.因此,式(8)中的∀x∈{1,2,…,N},将变为∀x∈Ωx.

5 博弈机制流程图

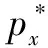
6 仿真结果与性能分析

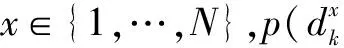
定义3 如果非授权用户始终认为其它非授权用户有和自己一样的信道判决结果,这种方法记为NP方法.

当代价函数的满意度系数为1.2,非授权用户数为15时,图3给出了价格系数变化时平均容量与平均功率的比值变化关系.当价格系数增大时,比值增大.这是因为随着价格系数的增大,非授权用户对发射功率所付出的代价增大,因此非授权用户更加注重单位功率的利用率.

如图4所示,价格系数为1.5,非授权用户数为15,随着满意度系数的增加,比值逐渐增加.但在保证通信质量的前提下上升趋势在达到一定程度后趋于平缓.可见,当满意度系数较小时,非授权用户的信干比要较高

大,且随着满意度系数的变化发射功率变化较快,使得容量功率比变化较快.当满意度系数较大时,情况正好相反.

从图3和图4中还可看到,NP方法的性能最差,HMM方法的性能最好.这是因为HMM方法和MAP方法都进行了推测,使得非授权用户能更准确地获得竞争对集合.MAP方法只利用当前时刻的信息进行推测,推测结果无法得到修正,而HMM方法应用观测状态序列进行推测,能够更准确推测参与博弈的用户,因此性能最好.

为了进一步比较方法的性能,引入KG[18]方法和NPCAGT[19]方法.值得注意的是HMM、MAP、NP方法的代价函数一致,而和KG方法、NPCAGT方法不同.设HMM、MAP、NP方法的满意度系数为10,价格系数为10.如图5所示,随着非授权用户数的增加,系统中各方法的平均容量与平均功率的比值逐渐降低.用户数的增加导致在基站处非授权用户相互间的干扰加大,降低了传输容量,因此使得比值逐渐降低.对比可以发现,HMM方法的性能最好,MAP方法次之,这是因为它们能够对干扰用户(即博弈对手)进行推测,从而能够选择相对合理的发射功率,提高功率效率,而且HMM方法的推测准确率更高.其余三种方法由于不能推测干扰用户,所以功率效率相对较低.进一步比较可以看出,对于KG方法、NP方法、NPCAGT方法,由于本文设计的代价函数在满足通信质量后,继续增大功率时付出的代价相对于KG方法和NPCAGT方法的代价要高,减少了能量的浪费,因此NP方法的功率效率相对较高.

图6显示了五种算法在不同非授权用户数条件下的平均信干比对比.仿真中设定的目标信干比为6dB,显然HMM方法的信干比最接近于目标信干比.这也是因为一方面HMM方法的代价函数在满足通信质量后,继续增大功率时付出的代价相对于KG方法和NPCAGT

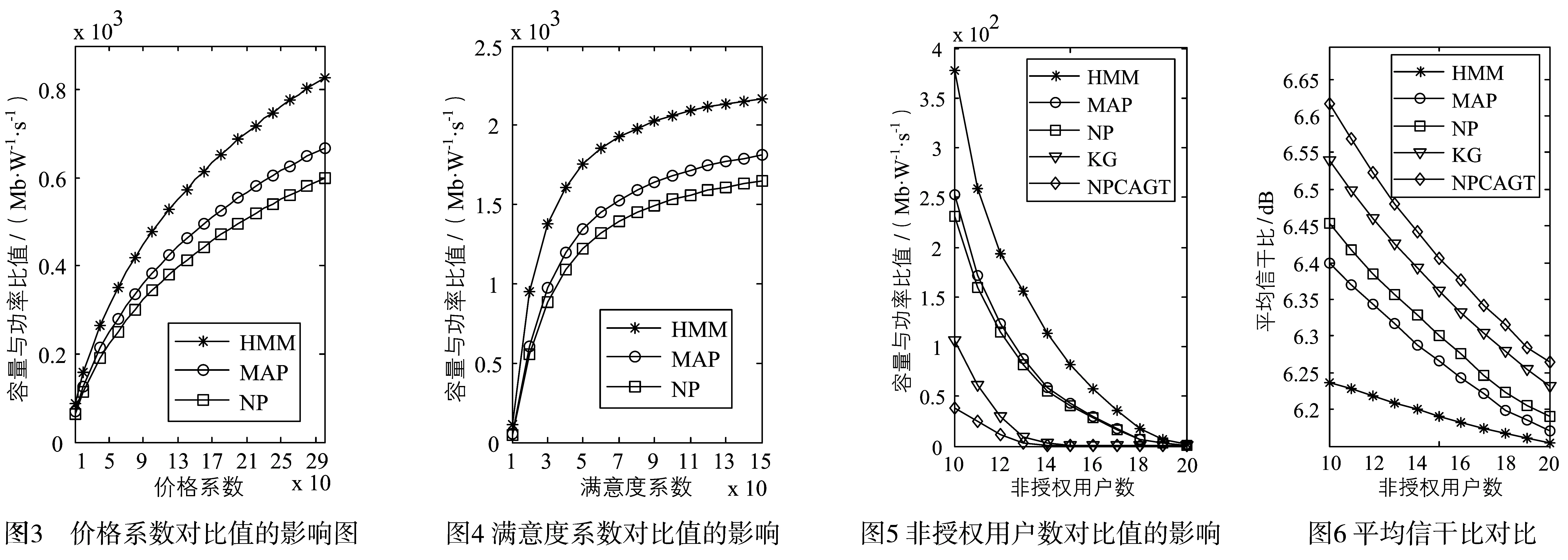
面,相对于其它方法,HMM方法能够更准确推测干扰用户(即博弈对手)数,在满足用户目标信干比需求的情况下限制其发射功率,提高功率效率的同时能够保证用户的通信质量.

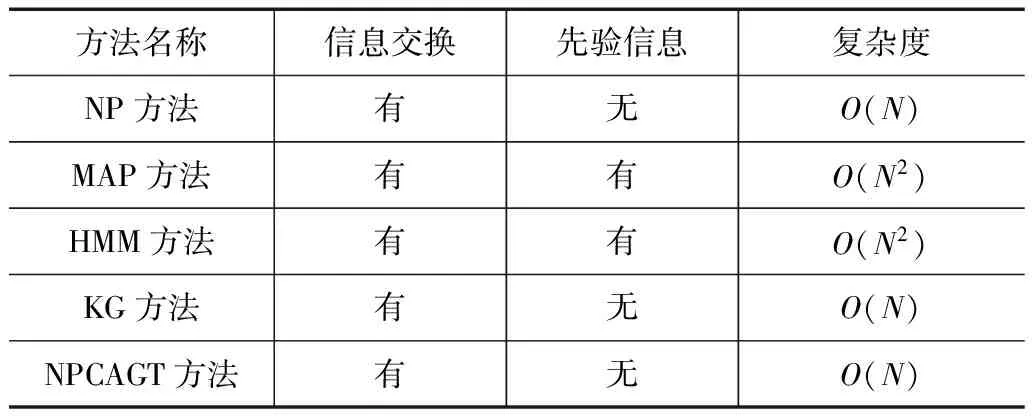
表1 实现代价

表1是5种方法在信息交换、先验信息和复杂度三个方面的比较.由表1可见在每帧的开始,5种方法的实现都需要交换信道增益h和噪声N0信息,如果信道的变化比较慢,那么信息交换的频率比较小,而且MAP方法和HMM方法的实现需要知道先验信息,即非授权用户对信道状态的判决能力.在NP方法、KG方法、NPCAGT方法中N个非授权用户只需各自判断当前时隙的信道状态即可,而MAP方法还要分别推测其他人的判决状态,则MAP方法的复杂度为O(N2).HMM方法在推测时仅需应用t-1时隙的先验概率计算t时隙的后验概率,因此其复杂度也为O(N2).由此可见,虽然参与博弈的非授权用户获取对手的信息越多、越准确,系统的性能越好,但这是以增加复杂度为代价的.

7 结束语

在分布式的认知无线网络中,为平衡非授权用户容量和功率的关系,以无线频域信道作为认知对象,针对不同用户对信道检测结果的差异,以及信道检测结果的非独立性,提出了一种隐马尔科夫模型.在基于该模型的功率博弈机制下,非授权用户可以通过自身判决的信道状态推测出竞争对手判决的信道状态,从而更准确地确定出当前时隙内的竞争对手集合,使得非授权用户在博弈竞争过程中能选取更优的发射功率.仿真结果和性能分析证明了所提机制有更大的容量功率比,具有更好的功率效率,但这是以较高的实现代价换取的.

[1]Wang B B,Liu K J R.Advances in cognitive radio networks:a survey [J].IEEE Journal of Selected Topics in Signal Processing,2011,5(1)：5-23.

[2]Liang Hui,Zhao Xiaohui.Dynamic programming based power control algorithm with primary user QoS guarantee for cognitive radio networks [J].Chinese Journal of Electronics,2013,22(2)：353-358.

[3]Zhao Junhui,Guan Xin,Li Xiuping.Power allocation based on genetic simulated annealing algorithm in cognitive radio networks [J].Chinese Journal of Electronics,2013,22(1)：177-180.

[4]Lu K W,Zhang L J,Yang J.An efficient SIR-first adaptive power control method in cognitive radio network [A].Global High Tech Congress on Electronics (GHTCE)[C].Shenzhen：IEEE，2012.91-94.

[5]Chen Y,Yu G D,Zhang Z Y,et al.On cognitive radio networks with opportunistic power control strategies in fading channels [J].IEEE Transactions on Wireless Communications,2008,7(7)：2752-2761.

[6]Sanchez S M,Souza R D,Fernandez E M G,et al.Rate and energy efficient power control in a cognitive radio Ad hoc network [J].IEEE Signal Processing Letters,2013,20(5)：451-454.

[7]Rawat D B,Bista B B,Yan G J.Precoder adaptation and power control in wireless Ad hoc networks for rate maximization [A].International Conference on Network-Based Information Systems (NBiS)[C].Tirana：ACM,2011.30-34.

[8]Osborne M J,Rubinstein A.A Course in Game Theory [M].Cambridge,Mass：MIT press,1994.24-29.

[9]Srivastava V,Neel J,Mackenzie A B,et al.Using game theory to analyze wireless Ad hoc networks [J].IEEE Communications Surveys and Tutorials,2005,7(4)：46-56.

[10]Rabiner L R.A tutorial on hidden Markov models and selected applications in speech recognition [J].Proceedings of the IEEE,1989,77(2)：257-286.

[11]Dashti M,Azmi P,Navaie K.Resource allocation for Underlay CDMA cognitive radio networks [A].2012 IEEE Wireless Communications and Networking Conference (WCNC)[C].Shanghai：IEEE,2012.2792-2796.

[12]Kim K J,Kwak K S,Choi B D.Performance analysis of opportunistic spectrum access protocol for multi-channel cognitive radio networks [J].Journal of Communications and Networks,2013,15(1)：77-86.

[13]Xing Y P,Chandramouli R.Stochastic learning solution for distributed discrete power control game in wireless data networks [J].IEEE/ACM Transactions on Networking,2008,16(4)：932-944.

[14]Muqattash A,Krunz M.CDMA-based MAC protocol for wireless Ad hoc networks [A].2003 ACM International Symposium on Mobile Ad hoc Networking & Computing (MobiHoc)[C].New York：ACM,September 2003.153-164.

[15]张立,郑国莘,贾东立,朱亚洲.知无线电网络中控制信道预约的MAC协议 [J].北京邮电大学学报,2011,33(4)：79-82. Zhang L,Zheng G X,Jia D L,Zhu Y Z.A control channel reserving based MAC protocol for cognitive radio networks [J].Journal of Beijing University of Posts and Telecommunications,2011,33(4)：79-82.(in Chinese)

[16]Saraydar C U,Mandayam N B,Goodman D J.Efficient power control via pricing in wireless data networks [J].IEEE Transactions on Communications,2002,50(2)：291-303.

[17]Cai X,Giannakis G B.A two-dimensional channel simulation model for shadowing processes [J].IEEE Transactions on Vehicular Technology,2003,52(6)：1558-1567.

[18]Koskie S,Gajic Z.A Nash game algorithm for SIR-based power control in 3G wireless CDMA networks [J].IEEE/ACM Transactions on Networking,2005,13(5)：1017-1026.

[19]Zhao C L,Guo Y.A novel distributed power control algorithm based on game theory [A].IEEE 5th International Conference on Wireless Communications,Networking and Mobile Computing (WiCom'09)[C].Beijing：IET,2009.1-4.

[20]Yates R D.A framework for uplink power control in cellular radio systems [J].IEEE Journal on Selected Areas in Communications,1995,13(7)：1341-1347.

朱 江(通信作者) 男,1977年出生,湖北荆州人,副教授,博士,研究方向为智能无线网络技术、无线网络资源管理.

E-mail：zhujiang@cqupt.edu.cn

张玉平 男,1987年出生,内蒙古赤峰人,硕士研究生,研究方向为认知无线电技术、无线网络资源管理.

E-mail：476705670@qq.com

A Game-Theoretic Power Control Mechanism Based on Hidden Markov in Imperfect Information Environment

ZHU Jiang,ZHANG Yu-ping

(ChongqingKeyLaboratoryofMobileCommunicationsTechnology,ChongqingUniversityofPostsandTelecommunications,Chongqing400065,China)

To solve the distributed power control issues in cognitive radio networks under imperfect information environment,according to the difference and independence of channel detecting results of different unlicensed users,a game-theoretic power control mechanism based on hidden Markov model (HMM) is proposed.By the HMM mode,unlicensed user can estimate whether competitors would take part in the game,which improves the information accuracy of game and allows the unlicensed users to choose an optimal transmission power.Simulation results indicate that the game-theoretic power control mechanism based on HMM can not only improve the power efficiency but also meet the target capacity compared with other cases.

imperfect information; hidden Markov; game-theoretic power control

2014-10-14;

2015-06-28；责任编辑：梅志强

国家自然科学基金(No.61102062，No.61271260)；重庆市科委自然科学基金(No.cstc2015jcyjA40050)

TN929.5

A

0372-2112 (2016)12-3004-07

��学报URL:http://www.ejournal.org.cn

10.3969/j.issn.0372-2112.2016.12.027