基于工艺参数扰动的IC参数成品率多目标优化算法
2017-01-10田江山
李 鑫,孙 晋,肖 甫,田江山
(1.江苏省安全生产科学研究院科技研发中心,江苏南京 210042; 2.南京邮电大学江苏省无线传感网高技术研究重点实验室,江苏南京 210013; 3.南京理工大学计算机科学与工程学院,江苏南京 210094)
基于工艺参数扰动的IC参数成品率多目标优化算法
李 鑫1,2,孙 晋3,肖 甫2,田江山3
(1.江苏省安全生产科学研究院科技研发中心,江苏南京 210042; 2.南京邮电大学江苏省无线传感网高技术研究重点实验室,江苏南京 210013; 3.南京理工大学计算机科学与工程学院,江苏南京 210094)
在芯片制造工艺中,参数扰动影响了集成电路(Integrated Circuit,IC)成品率,使不同参数成品率间存在着此消彼长的相互制约关系,而目前IC参数成品率优化算法却主要局限于单一优化目标问题.本文提出一种基于工艺参数扰动的参数成品率多目标优化算法.该算法针对漏电功耗成品率及芯片时延成品率,首先构建具有随机相关性的漏电功耗及芯片时延统计模型;随后根据其相互制约特性建立基于切比雪夫仿射理论的参数成品率多目标优化模型;最后利用自适应加权求和得到分布均匀的帕雷托优化解.实验结果表明,该算法对于具有不同测试单元的实验电路均可求得大约30个分布均匀的帕雷托优化解,不仅能够有效权衡多个优化目标间的相互制约关系,还可以使传统加权求和优化方法在帕雷托曲线变化率较小之处得到优化解.
可制造性设计;参数成品率;统计建模;多目标优化;帕累托最优
1 引言
随着半导体工艺水平的不断进步,IC特征尺寸减小,工艺参数扰动对当今IC参数成品率的影响正在日益加剧[1~5].此时,工艺参数扰动所引起的ULSI电路性能与设计指标背离,必然会引起依赖于工艺参数的性能参数成品率显著下降[6~8].而且,由于漏电功耗成品率和芯片时延成品率之间存在此消彼长的相互制约特性[9].因此,将漏电功耗和芯片时延同时作为优化目标进行成品率均衡优化,使芯片参数成品率达到最优就变得至关重要.
目前,国内外学者针对IC芯片参数成品率优化的研究主要还局限于单一优化目标[10~12].针对此情况,Mani等提出了一种二阶优化模型,在优化功耗成品率的同时一定程度上改进了时延成品率[13].此外,Hwang和Orshansky等还分别提出了基于时延成品率约束的芯片功耗优化算法,其在保证一定时延成品率的基础上提高了芯片的功耗成品率[14,15].然而,由于上述方法均未将漏电功耗及芯片时延同时作为优化目标进行参数成品率优化,因此忽略了漏电功耗成品率和芯片时延成品率之间的强相关特性.特别是当计算机芯片制造工艺发展到20nm制程后,Mani和Hwang等所提出的参数成品率优化算法会在很大程度上影响优化精度,具有一定的局限性.
针对以上问题,本文基于切比雪夫仿射理论(CAA)及自适应加权求和方法(AWS)提出一种新的功耗-时延成品率多目标优化算法.该算法首先考虑工艺参数扰动,确定具有随机相关性的漏电功耗和芯片时延概率统计模型,随后提出利用累积概率边界估算构建功耗-时延成品率多目标优化模型,并通过自适应加权求和得到一组分布均匀的帕雷托优化解.仿真实验结果表明,该方法不仅能够有效权衡多个优化目标间的相互制约关系,而且可以解决传统优化方法在帕雷托曲线变化率较小之处得不到优化解的问题.
2 漏电功耗及芯片时延统计模型
工艺参数扰动对IC芯片的影响可分为片内工艺扰动和片间工艺扰动两部分[16].此时,以ΔP表征任意工艺参数扰动,则ΔP可表示为:
ΔP=ΔPl+ΔPg
(1)
其中,ΔPl表示片内扰动,ΔPg表示片间扰动.
不失一般性,将有效沟道长度L、门限电压Vth和氧化层厚度Tox作为考虑的工艺参数扰动.此时,漏电功耗可描述为亚阈值电流Isub与栅极电流Igate之和的形式[3]:
Leakage=Isub,nom·eaΔL2+bΔL+cΔVth+Igate,nomedΔTox
(2)
其中,Isub,nom为亚阈值电流均值,Igate,nom为栅极漏电流的均值,变化量ΔL,ΔVth,ΔTox分别表示L、Vth和Tox所引起的工艺扰动影响.
在此根据式(1),L、Vth、Tox所引起的工艺扰动影响可进一步表示为:
ΔL=ΔLl+ΔLg
ΔVth=ΔVth,l+ΔVth,g
ΔTox=ΔTox,l+ΔTox,g
(3)
其中,ΔLl、ΔLg、ΔVth,l、ΔVth,g、ΔTox,l、ΔTox,g分别为L、Vth、Tox的片内工艺扰动及片间工艺扰动.
将式(3)分解模型代入式(2),则漏电功耗统计模型可改写为:

(4)
同理,针对芯片时延统计模型,将一阶泰勒展开引入芯片时延建模过程[17],则芯片时延方程可线性近似为:
(5)
其中,Dnom表示芯片时延均值,∂D/∂Pi表示工艺参数扰动Pi的时延灵敏度.
此时,将式(3)引入式(5)线性方程,则芯片时延模型可建立为:
Delay=Dnom+(gΔLl+hΔVth,l+kΔTox,l)
+(gΔLg+hΔVth,g+kΔTox,g)
(6)
其中,g,h,k为相应的灵敏度参数.
在此需特别说明的是,由于漏电功耗和时延的统计模型均与相同工艺扰动参数成函数关系,因此它们是具有随机相关性的.
3 基于CAA理论的功耗-时延成品率多目标优化模型
3.1 CAA仿射逼近
CAA理论是用于处理基于不确定性区间估计问题的一种分析方法[18,19].根据该方法,一个部分确定的随机变量x可以表示成一阶仿射形式,记为x′:
x′=x0+x1ε1+x2ε2+…+xnεn
(7)
其中,常量x0为标称值(均值).εi,(i=1,…,n)为不确定性符号,表示标称值扰动中的独立组成部分.xi表示相应εi的扰动系数.
在此,对于任意常量α,ζ,当二元运算z′←f(x′,y′)中f为仿射函数时,共有三种仿射运算可将其表示为仿射形式:
(8)
然而,当函数f为非仿射函数时,z′却无法直接以仿射形式表示,此时,根据简单性和有效性原则,通常考虑利用自身为x′和y′仿射运算的函数对z′进行仿射逼近[20],其表达式为:
fa(ε1,…,εn)=αx′+βy′+ζ
(9)
随后,通过最大误差最小化的切比雪夫逼近方法确定式(9)中的优化系数α、β、ζ,即可保证仿射逼近的准确性.
3.2 基于CAA仿射逼近的累积概率边界估算
通常,一个仅部分确定的随机变量可通过P-box进行描述,其P-box曲线上下边界可通过分段线性概率边界方法(PLPB)进行切比雪夫逼近[20].逼近结果为分段线性的CDF上下边界函数,如图1所示:


(10)
(11)
同理,对于’-’操作有:
(12)
(13)

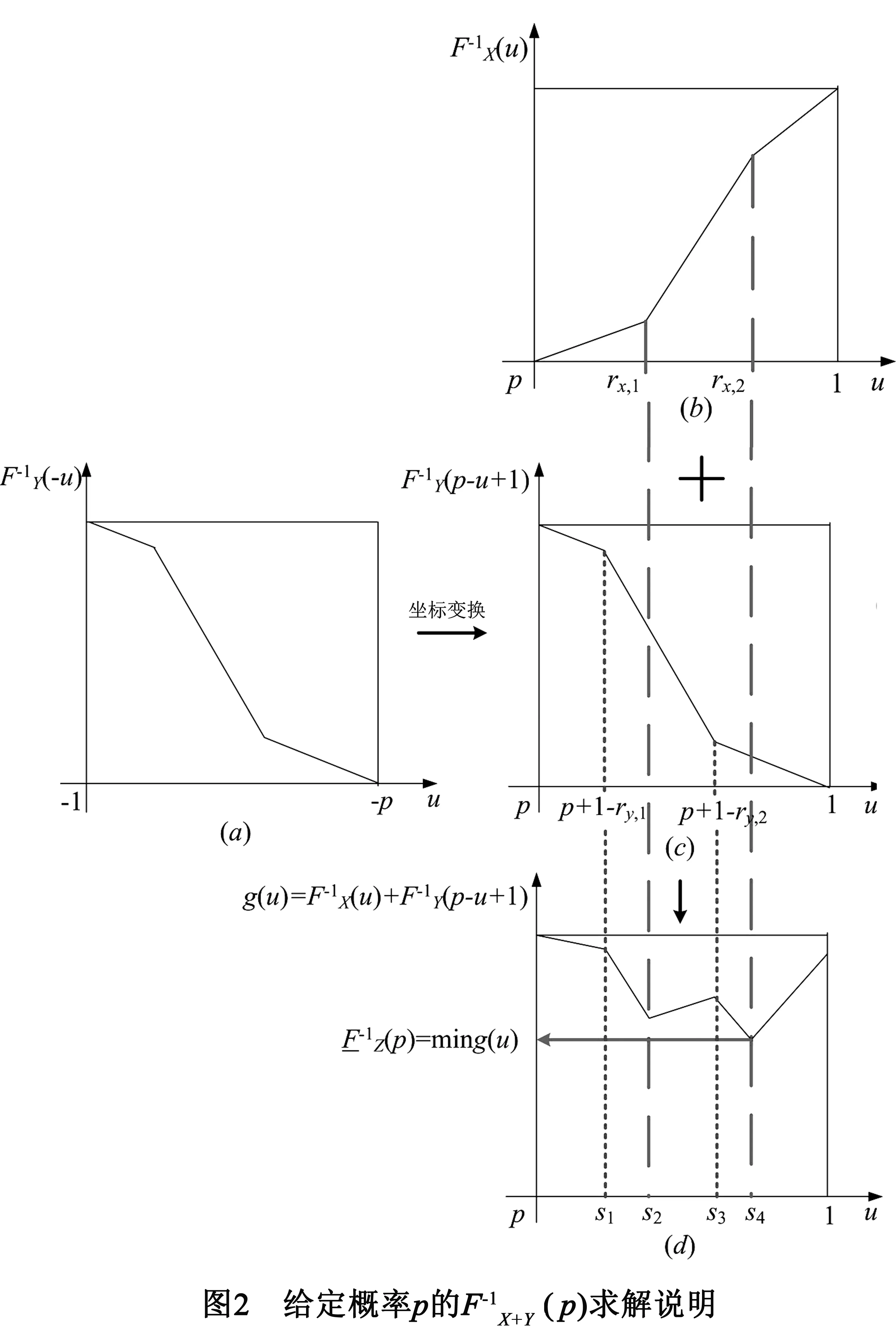
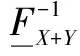
3.3 功耗-时延成品率多目标优化模型
在此,不失一般性,以漏电功耗统计模型为例对其成品率YLeakage进行估算.而芯片时延成品率YDelay则可依同样方法获得.
首先,对于具有随机扰动的工艺参数P,其仿射形式有:
P′=P0+1·ε
(14)
其中,P0为工艺参数均值,ε为相应的具有零均值的部分确定随机扰动.
此时,根据文献[22]对漏电功耗模型进行仿射表示,可得:
(15)
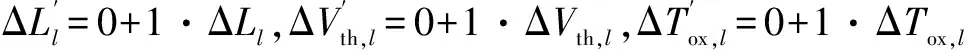

在此,为对漏电功耗成品率进行估算,仅考虑CDF的下边界FLeakage,其几何意义如图3所示.
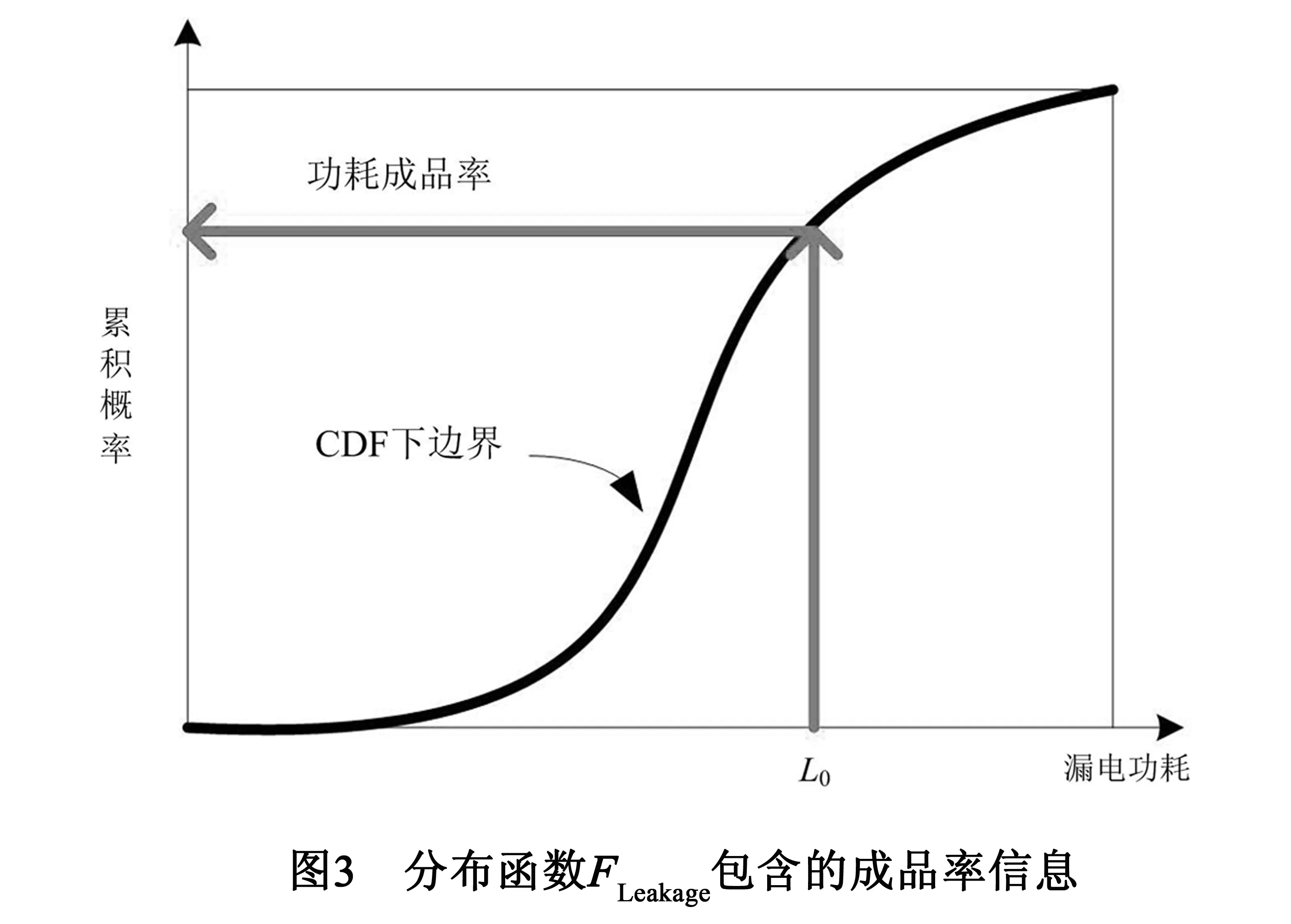
此时,若L0为漏电功耗标称值,则该标称值下的成品率可表示为:
YLeakage=FLeakage(L0)=P(Leakage (16) 同理,芯片时延成品率为: YDelay=FDelay(D0)=P(Delay (17) 由于漏电功耗与芯片时延均可表示成工艺参数扰动函数的形式,因此芯片参数成品率多目标优化模型可构造为: (18) 其中,FLeakage和FDelay分别为漏电功耗与芯片时延的CDF下边界,LL、Vth,L、Tox,L和LU、Vth,U、Tox,U分别为L、Vth和Tox的优化边界,L0、D0为事先确定的漏电功耗与芯片时延标称值. 不失一般性,假设目标函数向量f(L,Vth,Tox)=[f1(L,Vth,Tox),f2(L,Vth,Tox)]分别代表漏电功耗成品率和芯片时延成品率.此时,根据传统加权求和方法,归一化后的单目标优化模型可表示为: (19) 一般来说,由于式(19)优化模型所得的优化解并不是均匀分布的,其解大都集中于帕雷托曲线变化率较大的地方.因此,为使优化解均匀分布,需进一步细化求解以获得曲线变化率较小处的帕雷托优化解.此时,优化模型中需细化求解的区域可通过计算相邻解间距离确定:若相邻解间距离小于预设值,则该区域不需细化;反之,则通过引入新的约束条件建立细化区域子优化模型进行优化求解.其具体求解过程如图4所示,其中P1,P2为第i个细化区域的两个端点,δf为我们预定义的偏移距离常量. 在此,引入新的约束条件如图4(a)所示,新的优化区域为在原区域基础上分别从端点P1,P2沿f1,f2反方向偏移δ1和δ2距离,其值由δf与θ确定.此时,在该子区域内根据加权求和方法建立子优化模型为: (20) 通过求解式(20)子优化模型,细化区域内新的优化解即可被确定,如图4(b)所示.在所有细化区域内重复以上优化过程直至所有满足条件的优化解均被求得,此时即可得到分布均匀的帕雷托优化解. 本文所有实验均在配置为3.0GHz,2.0GB RAM的PC上以MATLAB完成.仿真实验通过国际电路与系统研讨会(ISCAS)基准电路进行算法有效性验证,而漏电功耗及芯片时延统计模型中系数则由HSPICE仿真结果拟合获得. 在此,假设所有工艺参数均服从截断高斯分布,L、Vth、Tox的3σ值分别为20%、10%、8%.并且对所有的工艺参数,片内扰动与片间扰动各占50%. 5.1 CDF函数边界估算方法有效性验证 为证明本文所提出的CDF函数边界估算方法可以处理工艺参数相关性为任意的情况,我们选择C432电路以及蒙特卡罗仿真来进行验证实验.在实验中,我们比较三种相关性情况:正相关性,负相关性,无相关性.图5(a)、图5(b)分别给出了不同相关性条件下的漏电功耗和芯片时延CDF下边界曲线及本文方法所得的CDF下边界曲线.由图中曲线易知,所有相关性情况均有效的包含在本文方法所得的CDF下边界曲线内.因此,该方法可以有效估计各种相关性情况的累积分布函数. 除此以外,由于漏电功耗模型中的指数项将显著增加工艺参数扰动对漏电功耗的影响,因此漏电功耗相较于芯片时延对工艺参数扰动具有更高的灵敏度,漏电功耗的变化范围较芯片时延要大的多.该点也可由图5(a)、图5(b)直观的看出. 5.2 多目标优化算法有效性验证 在此,我们假设式(20)模型中芯片时延标称值D0为 1.13倍,并对其进行算法有效性验证实验.表1给出了特定权值因子下对基准电路优化所得的优化解、优化解总数及算法运行时间.由表1可看出,每个实验电路大约可得到30个优化解. 为进一步说明多目标优化算法的有效性,本文在不同标称值限制下,对C432电路进行优化求解.当芯片时延标称值控制在均值的1.02倍时,图6(a)给出了不同漏电功耗标称值下的优化曲线;当漏电功耗标称值控制在均值的1.13倍时,图6(b)给出了不同时延标称值下的优化曲线.其中,每条曲线代表漏电功耗-芯片时延优化模型下的帕雷托曲线,而曲线上的各点则代表了确定的帕雷托优化解. 表1 固定功耗及时延标称值所得部分成品率优化解 考虑工艺参数扰动的随机相关性及漏电功耗成品率、芯片时延成品率间的相互制约特性,提出一种基于工艺参数扰动的IC参数成品率多目标优化算法.该算法首先构建漏电功耗及芯片时延的概率统计模型,然后考虑漏电功耗成品率及芯片时延成品率间的相互制约特性,建立功耗-时延成品率多目标优化模型,并采取自适应加权求和方法得到分布均匀的帕雷托优化解.实验结果表明,本文提出的优化算法对于每个实验电路均可求得大约30个分布均匀的帕雷托优化解,不仅能够有效权衡漏电功耗成品率及芯片时延成品率间的相互制约关系,还可解决传统优化方法在帕雷托曲线变化率较小的地方求解不到优化解的问题. [1]肖杰,江建慧,等.一个面向缺陷分析的电路成品率与可靠性关系模型[J].电子学报,2014,42(4):747-755. Xiao Jie,Jiang Jian-hui,et al.A defect analysis-oriented relation model of circuit yield and reliability[J].Acta Electronica Sinica,2014,42(4):747-755.(in Chinese) [2]Banerjee A,Chatterjee A.Signature driven hierarchical post-manufacture tuning of RF systems for performance and power[J].IEEE Transactions on VLSI Systems, 2015,23(2):342-355. [3]Radfar M,Singh J.A yield improvement technique in severe process,voltage,and temperature variations and extreme voltage scaling[J].Microelectronics Reliability,2014,54(12):2813-2823. [4]Mani M,Devgan A,Orshansky M.An efficient algorithm for statistical minimization of total power under timing yield constraints[A].Proceedings of Design Automation Conference[C].California,USA:ACM,2005.309-314. [5]李鑫,Janet M Wang,等.工艺随机扰动下非均匀互连线串扰的谱域方法分析[J].电子学报,2009,37(2):398-403. Li Xin,Janet M Wang,et al.Spectral method for analysis of crosstalk of non-uniform RLC interconnects in the presence of process variations[J].Acta Electronica Sinica,2009,37(2):398-403.(in Chinese) [6]Liu X X,Palma-Rodriguez A A,Rodriguez-Chavez S.Performance bound and yield analysis for analog circuits under process variations[A].Proceedings of The Asia and South Pacific Design Automation Conference[C]. Yokohama,Japan:ACM,2013.761-766. [7]Wei W E,Li H Y,Han C Y.A flexible TFT circuit yield optimizer considering process variation,aging,and bending effects[J].IEEE/OSA Journal of Display Technology,2014,10(12):1055-1063. [8]卜登立,江建慧.基于对偶逻辑的混合极性RM电路极性转换和优化方法[J].电子学报,2015,43(1):79-85. Bu Deng-li,Jiang Jian-hui.Dual logic based polarity conversion and optimization of mixed polarity RM circuits[J].Acta Electronica Sinica,2015,43(1):79-85.(in Chinese) [9]Srivastava A,Kaviraj C,et al.A novel approach to perform gate-level yield analysis and optimization considering correlated variations in power and performance[J].IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems,2008,27(2):272-285. [10]Xie L,Davoodi A.Robust estimation of timing yield with partial statistical information on process variations[J].IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems,2008,27(12) 2264-2276. [11]Orshansky M,Bandyopadhyay A.Fast statistical timing analysis handling arbitrary delay correlations[A].Proceedings of Design Automation Conference[C].California,USA:ACM,2004.337-342. [12]Rao R,Srivastava A,et al.Statistical analysis of subthreshold leakage current for VLSI circuits[J].IEEE Transactions on Very Large Scale Integration Systems,2004,12(2):131-139. [13]Mani M,Devgan A,et al.A statistical algorithm for power-and timing-limited parametric yield optimization of larger integrated circuits[J].IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems,2007,26(10):1790-1802. [14]Hwang E J,Kim W,Kim Y H.Timing yield slack for timing yield-constrained optimization and its application to statistical leakage minimization[J].IEEE Transactions on Very Large Scale Integration Systems,2013,21(10):1783-1796. [15]Orshansky M.Statistical minimization of total power under timing yield constraints[A].Proceedings of IEEE International Conference on Integrated Circuit Design & Technology[C].Grenoble,France:IEEE,2006.1-4. [16]Mande S S,Chandorkar A N,Iwai H.Computationally efficient methodology for statistical characterization and yield estimation due to inter-and intra-die process variations[A].Proceedings of Asia Symposium on Quality Electronic Design[C].Penang,Malaysia:IEEE,2013.287-294. [17]Sheng Y,Xu K,Wang D,Chen R.Performance analysis of FET microwave devices by use of extended spectral-element time-domain method[J].International Journal of Electronics,2013,100(5):699-717. [18]Sun J,Huang Y,et al.Chebyshev affine arithmetic based parametric yield prediction under limited descriptions of uncertainty[A].Proceedings of The Asia and South Pacific Design Automation Conference[C].Seoul,Korea:ACM,2008.531-536. [19]Zhu W,Wu Z.The stochastic ordering of mean-preserving transformations and its applications[J].European Journal of Operational Research,2014,239(3):802-809. [20]Stolfi J,Figueiredo L H.Self-validated numerical methods and applications[A].Proceedings of Brazilian Math.Colloq.Monograph[C].Netherlands:Academic Press,1997.15-20. [21]Williamson R C,Downs T.Probabilistic arithmetic I:numerical methods for calculating convolutions and dependency bounds[J].International Journal of Approximate Reasoning,1990,(4):89-158. [22]Tiwary S K,Tiwary P K,Rutenbar R A.Generation of yield-aware Pareto surfaces for hierarchical circuit design space exploration[A].Proceedings of Design Automation Conference[C].California,USA:ACM,2006.31-36. 李 鑫 男,1983年2月出生于江苏省徐州市.2009年毕业于南京理工大学计算机学院.现为江苏省安全生产科学研究院高级工程师,从事VLSI计算机辅助设计与芯片可靠性估计及优化方面的研究工作. E-mail:lin65002@hotmail.com 孙 晋 男,1983年5月出生于江苏省淮安市.2011年毕业于亚利桑那大学电子与计算机工程系.现为南京理工大学计算机科学与工程学院副教授.从事集成芯片鲁棒性设计与多核片上网络低功耗设计方面的研究工作. E-mail:sunj@njust.edu.cn A Multi-objective Optimization Framework for Robust IC Parametric Yield Predication Under Process Variations LI Xin1,2,SUN Jin3,XIAO Fu2,TIAN Jiang-shan3 (1.TechnologyInnovationCenter,JiangsuAcademyofSafetyScienceandTechnology,Nanjing,Jiangsu210042,China; 2.JiangsuHighTechnologyResearchKeyLaboratoryforWirelessSensorNetworks,NanjingUniversityofPostsandTelecommunications,Nanjing,Jiangsu210013,China;3.SchoolofComputerScienceandEngineering,NanjingUniversityofScienceandTechnology,Nanjing,Jiangsu210094,China) Process variations lead to a significant degradation of IC parametric yield,and they also tend to cause a negative correlation between different parametric yields.However,previous yield optimization works are limited to deal with single objective problem.To deal with the above-mentioned limitation,this paper proposes a multi-objective optimization framework for co-optimization of power and timing yields under process variations.The proposed method starts with establishing explicit statistical models for power and timing metrics respectively.Then considering the negative correlation between the metrics,we employ Chebyshev affine arithmetic to formulate a multi-objective optimization model,optimize power and timing yields simultaneously by adaptive weighted sum method,and provide a well-distributed set of Pareto-optimal solutions.Experimental results demonstrate that the proposed method explores about 30 well-distributed solutions for each benchmark circuit with different test units.In addition,it can not only balance the restricted correlation between multiple optimization objectives,but make the traditional weighted sum method to get optimal solutions on the Pareto curve where change rate is small. design for manufacturability;parametric yield;statistical modeling;multi-objective optimization;Pareto optimality 2015-05-11; 2015-07-01;责任编辑:覃怀银 TN47 A 0372-2112 (2016)12-2960-07 ��学报URL:http://www.ejournal.org.cn 10.3969/j.issn.0372-2112.2016.12.0214 基于AWS的多目标优化算法
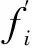

5 实验结果与比较



6 结论


