一种应用于虚拟现实的基于网格变形的立体图像生成方法

李大锦

(山东师范大学传媒学院数字媒体系,山东济南,250014)

一种应用于虚拟现实的基于网格变形的立体图像生成方法

李大锦

(山东师范大学传媒学院数字媒体系,山东济南,250014)

文章针对虚拟现实系统,介绍了立体图像的生成方法.提出了利用单个相机通过不同的投影变换来拍摄双眼图像.基于单相机拍摄的方法,分析了立体图像的视差形成机制,给出了有头跟踪设备和无头跟踪设备两种情况下双眼图像的视差变换矩阵.进一步分析了视差大小、感知深度、感知变形和模型变形之间的联系,将视差的产生归结为模型的几何变形.提出可以通过模型的几何变形来控制视差和感知物体的变形,从而给出了一种基于模型网格变形的非线性深度映射方法.该方法能有效的减少因感知物体的变形而带来的视觉瑕疵,并能消除在头跟踪系统中因深度映射导致的图像漂移.

3D显示;网格变形;感知深度;深度映射

1 引言

立体显示是模拟人类的双眼视觉机制.人在双眼观察时,物体于左右眼中的成像在水平方向上会产生视差,人通过视差来形成深度感知[1,2].所以立体图像包括一对具有水平视差的图像,分别代表左右眼图像.如何产生和控制左右眼图像的视差是立体图像创建的关键问题.

立体图像的获取最直接的方法是利用双相机分别拍摄左右眼图像[3,4];另一种方法是基于图像合成的方法[5,6].基于双相机拍摄的方法是采用两个水平放置的相机,两个相机轴线可以平行或水平倾斜相交.基于图像合成的方法是在原有的单个或多个视点的图像基础上,合成新的视点图像[5～7].基于图像的方法借助像素的深度信息,对像素进行重新投影形成新的图像,由于在像素重新投影的过程中,容易产生空洞,而完美的实现空洞充填仍然是一个有待解决的关键问题[6,8].近几年来,图像变形技术逐渐被应用于立体图像[9,10],可以避免产生空洞,但是存在一个潜在的问题是容易造成左右眼图像投影的不一致[10].基于图像的生成方法主要应用在2D到3D图像转换,很难应用于实时渲染系统.

人们在长时间观看立体图像时容易引起视觉疲劳或不适.引起视觉疲劳的原因很多,既有图像质量的原因又有硬件性能等方面的原因.大量研究证明:长时间较大的调节与汇聚冲突是立体图像引起视觉疲劳的主要原因[11].感知深度范围越大,调节汇聚冲突也越大.在一定的观看条件下,存在一个观看者能承受的感知深度适宜区[12].Wopking[13]认为较舒适的感知深度对应的视差范围应小于1度.Patterson[1]认为感知深度范围应限制在DOF(Depth of Field)之内.从调节汇聚冲突的角度来考虑,如果人的注意力较多的集中于显示屏幕附近(视差接近0)可进一步减少视觉疲劳[12].

通过改变图像视差来改变感知深度,从而避免视觉疲劳,这种方法称为深度映射或视差映射[14].深度映射最直接的方法是在拍摄过程中,直接调整相机的轴距、汇聚距离等参数.如文献[3,4,15]分别根据场景深度和观看适宜区,计算出合适的相机轴距、辐辏等参数.但这些方法都是压缩全局感知深度的线性压缩.深度映射会使感知物体变形,Holliman[14]为减少重要图像内容的变形,将场景沿深度方向分成多个区段,不同区段采用不同的相机参数,但这种分段压缩方法在不同区段上仍然是线性映射,会导致相邻区段中物体变形的不一致.利用图像变形[9,10]来调整双眼图像视差可以实现非线性深度映射,但这种方法只能应用于立体图像的后期处理,无法应用于虚拟现实这样的实时渲染系统.在头跟踪虚拟现实系统中,由于深度映射会带来感知物体的变形,这种变形会导致感知物体随着头部的运动而产生水平方向上漂移[16].

在虚拟场景中,由于模型的几何属性和虚拟相机的投影变换都具有可控性,所以通过投影变换和模型几何的修改也可以控制视差的产生.本文正是基于这个思想,提出了虚拟现实系统中的立体图像生成方法,我们在前期研究[17]的基础上,讨论了带头跟踪设备和无头跟踪设备两种情况下的视差控制方法.本文的主要创新之处在于：

(1)通过双眼图像视差的几何分析,提出利用模型网格的变形来控制视差的思想;给出了在单相机空间内头跟踪和无头跟踪两种情况下的视差的矩阵表示.

(2)基于模型网格的变形,给出了一种平滑的非线性深度映射方法.该方法不仅简单、灵活,还能消除因视点运动而产生的图像漂移.

2 与视点无关的立体图像

在无头跟踪设备的虚拟现实系统中,立体图像的拍摄是假定观看者的双眼处于和物理屏幕平行的水平线上,观看者和屏幕的位置固定.所以双眼图像只和两个相机的位置和方向有关,与观看者的位置无关,我们可称之为与视点无关的立体图像.在这种情况下,因为立体图像对的水平视差与轴距成线性关系,所以我们可以利用投影矩阵产生视差,并用同一个相机通过不同的投影变换得到左右眼图像.

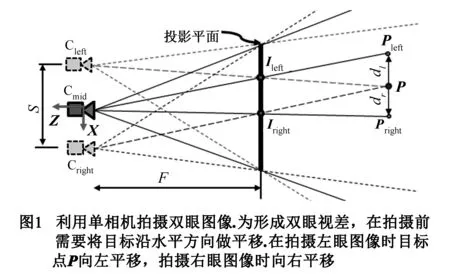
如图1所示：假设双相机的轴距为s;投影平面距相机距离为F;设点P(x,y,z)在左右相机上的投影为Ileft和Iright.在左右相机的中间位置创建一个中间相机Cmid,我们希望通过中间相机Cmid来获取左右图像,可以将点P沿水平方向平移使之在中间相机Cmid上的投影正好与其在左右相机上的投影重合.假设对应左右相机投影点的平移距离分别为dl和dr,根据几何关系可知：

该平移变换利用矩阵表示为：

MLpar和MRpar是为形成左右眼视差的变换矩阵,所以我们之为图像的视差矩阵.MLpar和MRpar是两个斜切变换,所以创建双眼图像的过程也可以理解为：先将模型进行斜切变换,然后再进行标准的透视投影.

3 与视点有关的立体图像

在有头跟踪设备(不包括HMD)的系统中,观看者的视点可以移动,但物理显示屏幕固定,立体图像和视点的位置和方向有关.所以我们称之为与视点有关的立体图像.拍摄这类图像,需要在虚拟环境中创建一个对应的固定的图像投影面,拍摄方向始终垂直于该投影面,相机坐标系的Y轴始终竖直向上.该投影面可以在世界坐标系中定义,投影前,首先将投影面变换到相机坐标系,并根据投影面的尺寸来定义视截体.所以视截体通常是一个非对称视截体.视截体会随着头部的运动而改变.

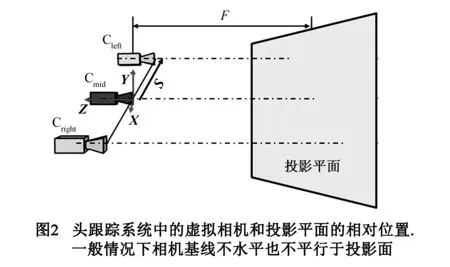
在一般情况下,相机基线不水平,和投影面也不平行.图2示意了虚拟世界中相机和投影平面相对位置的一般情况.和我们在无跟踪系统中所讨论的方法一样,我们在左右相机的中间位置建立一个中间相机Cmid,如图2所示,设从中间相机指向左相机的向量为S;中间相机距投影平面距离为F.从第2节的讨论知道,左右图像的视差可以由斜切变换生成.由于S不一定水平,所以在头跟踪系统中,除了产生水平视差,还会产生垂直视差.先考虑在特殊情况下,当向量S平行于投影平面时,可以利用2节的方法得到左眼图像的视差变换矩阵为：

(1)

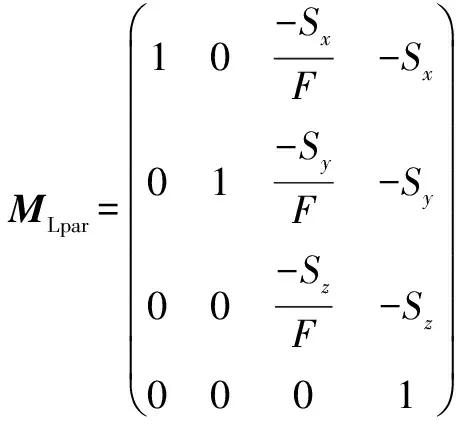
同理右眼的视差矩阵：

可以看出：在头跟踪立体显示系统中,为形成双眼视差,除了对模型做水平和竖直方向上的斜切变形,还需要做沿Z轴方向上的缩放变形.在单相机空间内,将视差矩阵MLpar和MRpar与标准的透视投影矩阵相乘即可得到左右图像的投影矩阵.

4 感知深度控制

4.1 感知变形

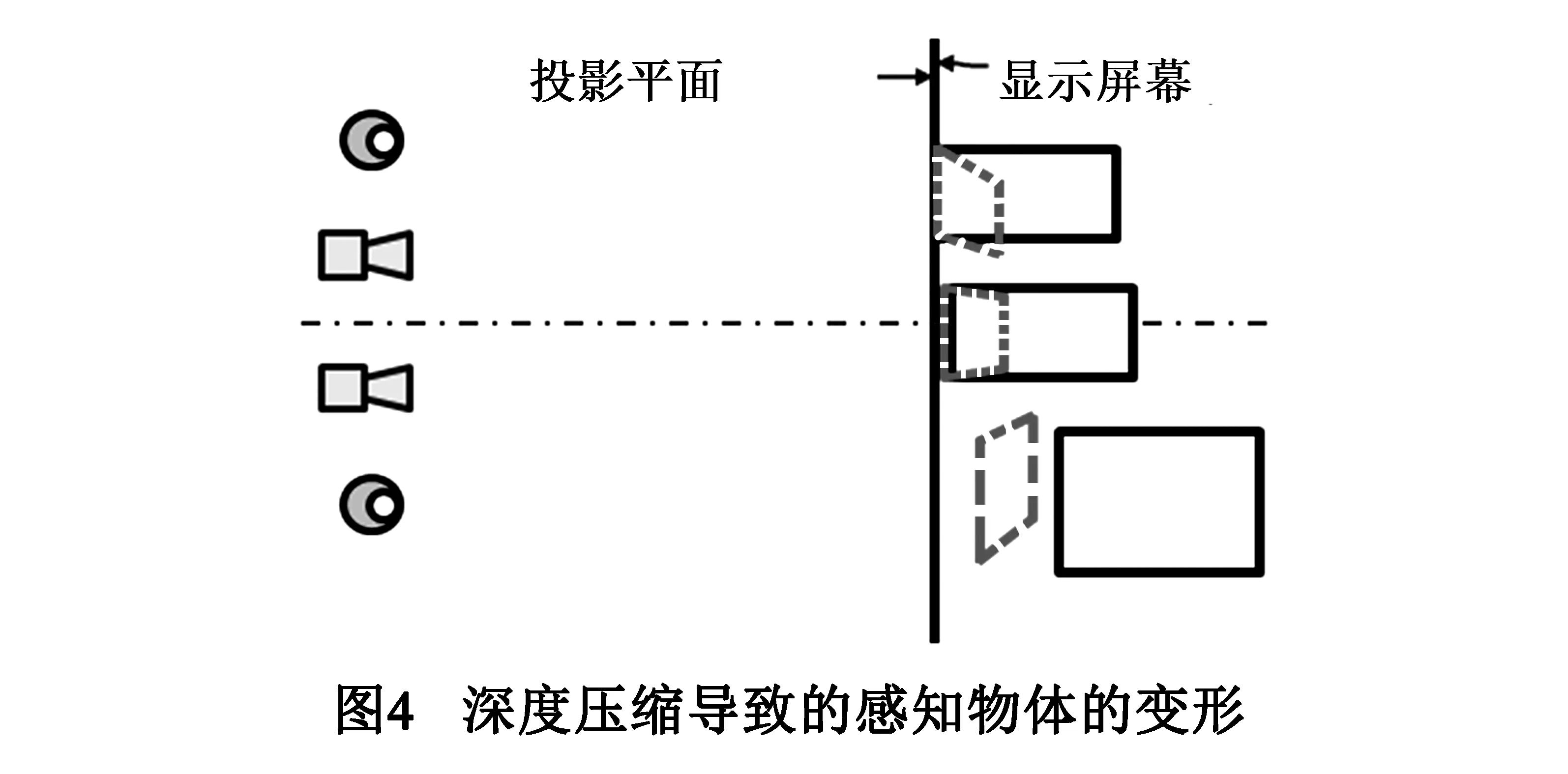
使用相对较小的相机轴距来拍摄立体图像会使是感知物体产生变形.图4示意了在相机轴距小于人的双眼距离的情况下,感知物体的变形情况.其中实线的矩形表示原始物体形状,虚线图形表示感知的物体的形状.可以看出：深度压缩所导致的物体变形包括沿水平方向上的斜切变形和沿深度方向上的收缩变形,其中深度方向上的收缩变形使感知深度变小.这种变形我们称之为感知变形.深度映射实质上是产生一定的感知变形,使感知范围位于观察适宜区.由第2、3节的讨论可知：可以对实际模型施加水平方向的斜切变形和深度方向上的缩放变形来生成左右图像,对模型的斜切和缩放变形的强度决定了图像视差的大小.所以如果将相机轴距等于观看者的双眼距离,感知深度可以直接通过模型网格的变形来控制.从这个意义上来说,感知变形可以通过模型变形来实现.如果要在不同深度区域使用不同的深度压缩比例,可以在不同的深度区域施加不同强度的模型变形.

4.2 非线性深度映射

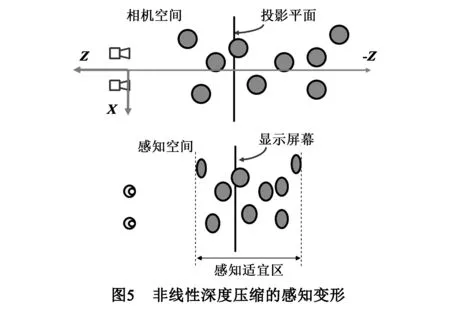
为减少感知变形带来的视觉瑕疵,一个有效的方法是采用非线性深度压缩,即将主要的观察内容施以较小的压缩比,而非重要内容用较大的压缩比[14,17].因为屏幕附近是人眼观看最适宜的区域,人在观看时也会更多的注意屏幕附近的影像.所以本文给出的非线性深度压缩方法是将场景总的感知深度压缩在适宜区范围,同时希望在屏幕附近的物体尽可能减少感知变形,而在较远的物体产生较大的感知变形.图5示意了本文的非线性深度压缩中感知物体的变形情况.

第2、3节可知,图像视差与感知深度可以由模型的水平斜切和深度方向上的缩放变形来控制.首先,我们来计算沿深度方向的缩放.我们以投影面作为变形的固定位置,将处于投影平面两侧的模型沿相机坐标系Z轴向投影平面挤压,顶点移动距离随深度增加而增加.在中间相机坐标系内,假设相机到投影平面的距离为F.任意某顶点的坐标为P(x,y,z),经过缩放变形后的坐标为P′(x′,y′,z′ ).对模型的的z坐标执行以下非线性变换：

(2)

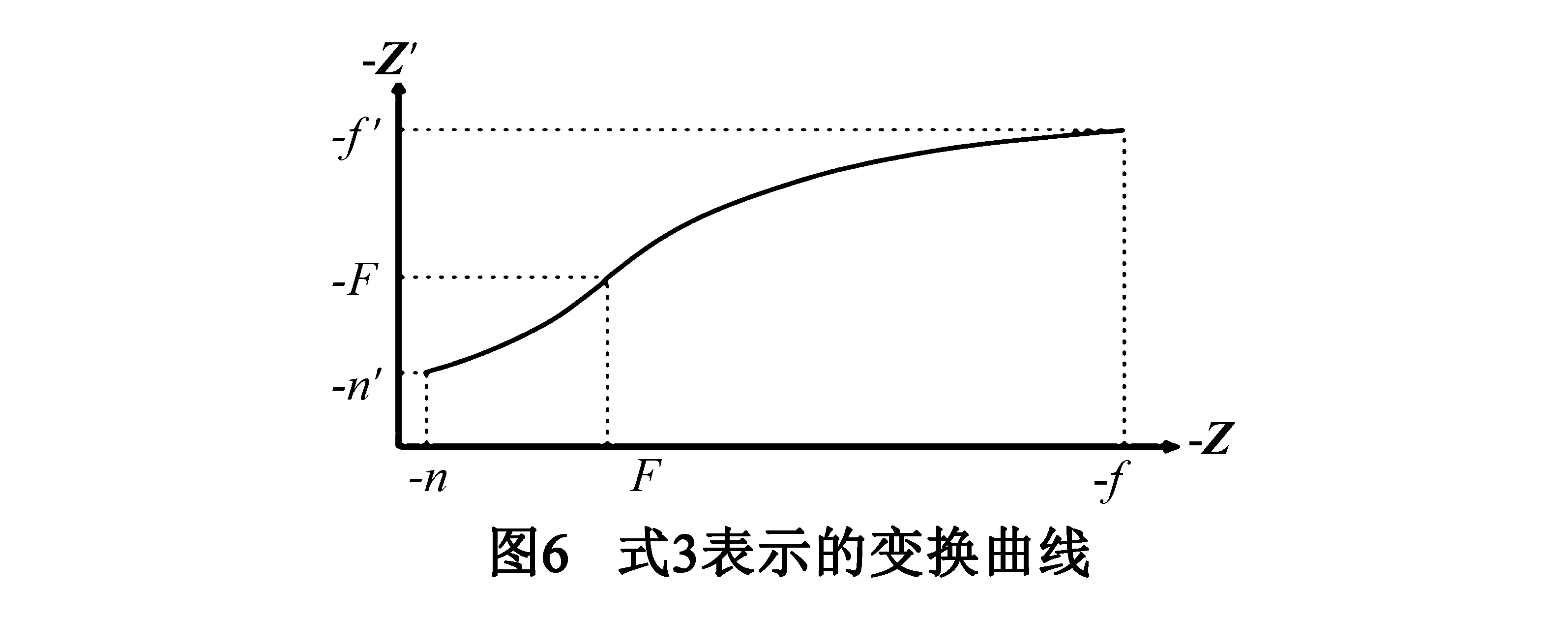
假设处于相机远裁剪面上的顶点(z坐标为-f)被挤压到坐标为-f′处,处于近裁剪面上的顶点(z坐标为-n)被挤压到-n′.将他们带入式(2),可求得a,b的值,得到最后的变换公式：

(3)

其中：A=F-f′,B=F-n′,C=F-f,D=F-n.f′和n′可根据一定观看条件下的观看适宜区来确定.如何计算适宜区的范围不是本文要讨论的内容,可参阅文献[1,18].图6是式(3)的变换曲线.

经过式(3)的缩放变形后,物体由于被移向投影面而使视差减小,从而减少了立体图像的感知深度.但是经过透视投影后的物体尺寸也发生变化.物体的透视尺度是感知物体相对深度的一个重要线索,单纯的进行深度方向上的缩放会严重减小场景中各物体的相对深度.所以在进行深度缩放的同时,在X、Y两个方向上也对模型进行缩放变形,以消除因物体被拉向投影面而造成的投影尺寸的改变.在中间相机坐标系内,当任意点P(x,y,z) 被平移到点P′(x′,y′,z′),要保证物体投影后的尺寸不发生改变,只需使P′在投影平面上的投影点和P相同.所以我们可对该点在XY方向上施加如下变换：

(4)

这两个式子分别是X、Y方向上的斜切变换,该斜切变形是以相机作为透视参考点,以相机坐标系的Z轴为基准线,物体向Z轴弯曲.图7表示了在X方向上的斜切变形.由于z′ 的变换是非线性变换,所以斜切变形也是非线性的.式(4)保证了物体由于相对深度不同而产生的透视效果.

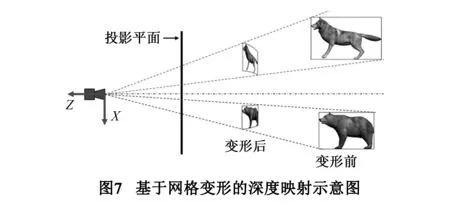
这样,立体图像的生成过程可概括为：首先根据观看条件确定双相机轴距、投影平面以及观看适宜区范围;创建中间相机,同时确定远近裁剪面的距离f、n;再根据观看适宜区确定f′ 和n′;将模型变换到中间相机空间,利用式(3)和式(4)对模型进行非线性缩放和斜切变形;最后通过视差矩阵MLpar和MRpar生成左右眼图像.4.3 头跟踪系统中的非线性深度映射

在头跟踪系统中,如果采用缩小相机轴距的方法进行深度映射,当头部左右运动时,感知到的图像会跟随头部运动而运动.Zachary等[16]给出了一个反向变形的矩阵用于消除线性深度映射中的图像漂移,但他们的方法只能用于线性压缩.本文提出的基于3D网格变形的非线性深度映射生成方法可以有效的解决图像漂移问题.

因为我们通过对模型在深度方向上进行缩放,可以直接减少图像视差和感知深度,所以我们不需要减少相机轴距,而直接将相机轴距等于观察者的双眼距离.但是如果按4.2节所讨论变形方法,以相机坐标系的原点为透视参考点计算模型的斜切变形也会随相机的移动而发生改变.如图8(a)所示,当相机从位置1移动到位置2时,因对应的透视参考点不同,斜切变形强度也发生变化.因此仍然会产生图像漂移.如果要消除图像漂移,只需要将透视参考点在XY方向上保持不变.

如图8(b)所示,我们在通过投影平面中心且与相机坐标系的Z轴平行的轴线(图8(b)中的红色点画线)上取一点作为投影参考点,该点距离投影面与相机到投影面的距离相等.设投影参考点在相机坐标系中的坐标为(Dx,Dy,0).则式(4)的斜切变换成为：

(5)

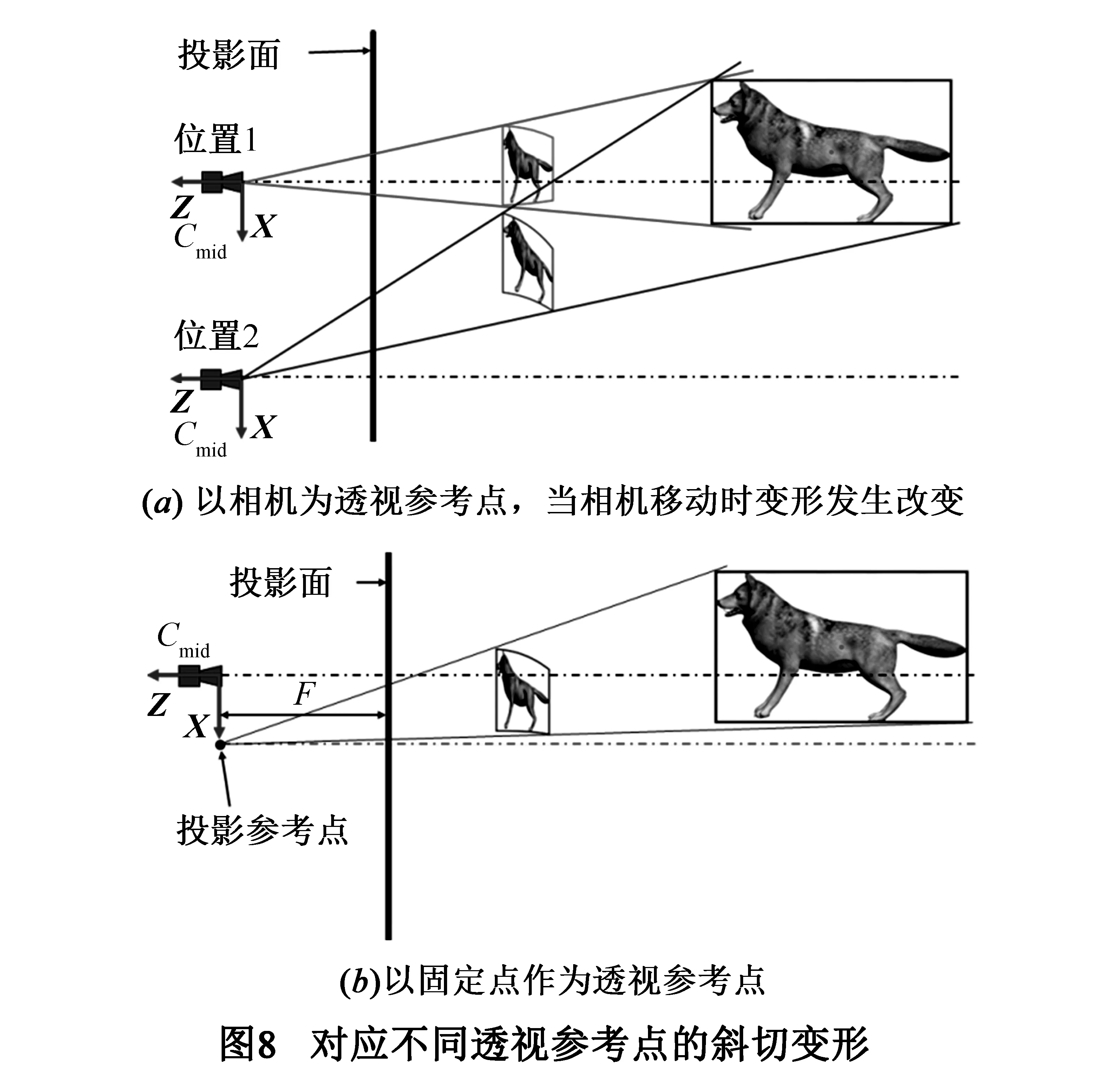
当相机轴距与观察者的双眼距离相同时,感知到的物体和实际场景一致,不会产生额外的感知变形.采用式5进行斜切变形,感知物体的形状和位置不会因相机在XY方向上的移动而发生改变,从而消除图像漂移现象.图9是我们根据感知深度几何绘制的线性映射、分段映射和本文方法的非线性映射在不同视点下的感知变形情况.其中,实线框为原始物体,粗虚线框为头部处于位置1时的感知物体形状,细虚线框为位置2时的感知物体形状.在线性映射(图9(a)) 中,相机轴距为人眼轴距的3/5;在分段映射(图9(b))中,我们将场景分为两段,在靠近投影面的一段采用的相机轴距和观察者双眼距离相等,第二段采用的相机轴距为人眼距离的3/5.在本文方法中(图9(c)),采用和人眼距离相等的相机轴距.从图中可以看出,本文方法在两个视点位置的感知物体的形状和位置完全相同.

5 结果和讨论

传统的通过调整相机轴距来控制视差尺度的方法缺乏灵活性,而且不能实现非线性深度压缩.本文从感知变形的角度来理解视差的产生,视差决定着感知变形,而视差可以不改变相机轴距的情况下,直接通过模型的变形来实现.因此在虚拟环境中,深度映射同样可以通过模型变形来实现.利用模型变形实现深度映射的主要优点在于其灵活性,可以方便的实现非线性深度压缩.

线性映射是一种均匀的深度映射,即感知深度压缩比例是恒定的.Holliman[14]的分段映射和本文的非线性映射都是非均匀的深度映射.分段映射法在不同的区域中使用不同的相机配置参数,所以每个分段区域都要单独进行一次拍摄,这致使渲染过程变得非常复杂.而基于模型网格变形的映射方法只需要采用统一的相机参数,经过一次拍摄即可完成.我们分别对线性映射、分段映射和本文的非线性映射方法所得到的结果进行了对比,同时还进行了主观评价实验.

5.1 感知变形

图10是线性映射、分段映射和本文的非线性映射的结果比较.三种方法都是把相同的场景映射到相同的整体深度范围之内.在图中的分段压缩方法中,我们将场景分为两段区域.从图中可以看出,在本文方法中,处于屏幕附近的恐龙和汽车的感知变形很小.而线性压缩只能采用相同的压缩比例,导致恐龙和汽车看起来明显的趋于扁平.虽然分段压缩也能得到不错的结果,但分段压缩方法对于同一个物体,只能采用相同的深度压缩比例,如果物体同时处于两个分段区域,只能按照一个区域的压缩比例进行压缩.这样会使物体之间的相对感知深度与实际不符.如第三行图中上部的立方体同时处于两个深度区域,采用了较大的压缩比例之后,其位置看起来被前移.分段压缩其本质上还是线性映射,不同的分段交界处压缩比例是不连续的,所以在头跟踪系统中,物体的感知深度压缩比例会随着视点的运动产生变形的跃变.

5.2 主观评价

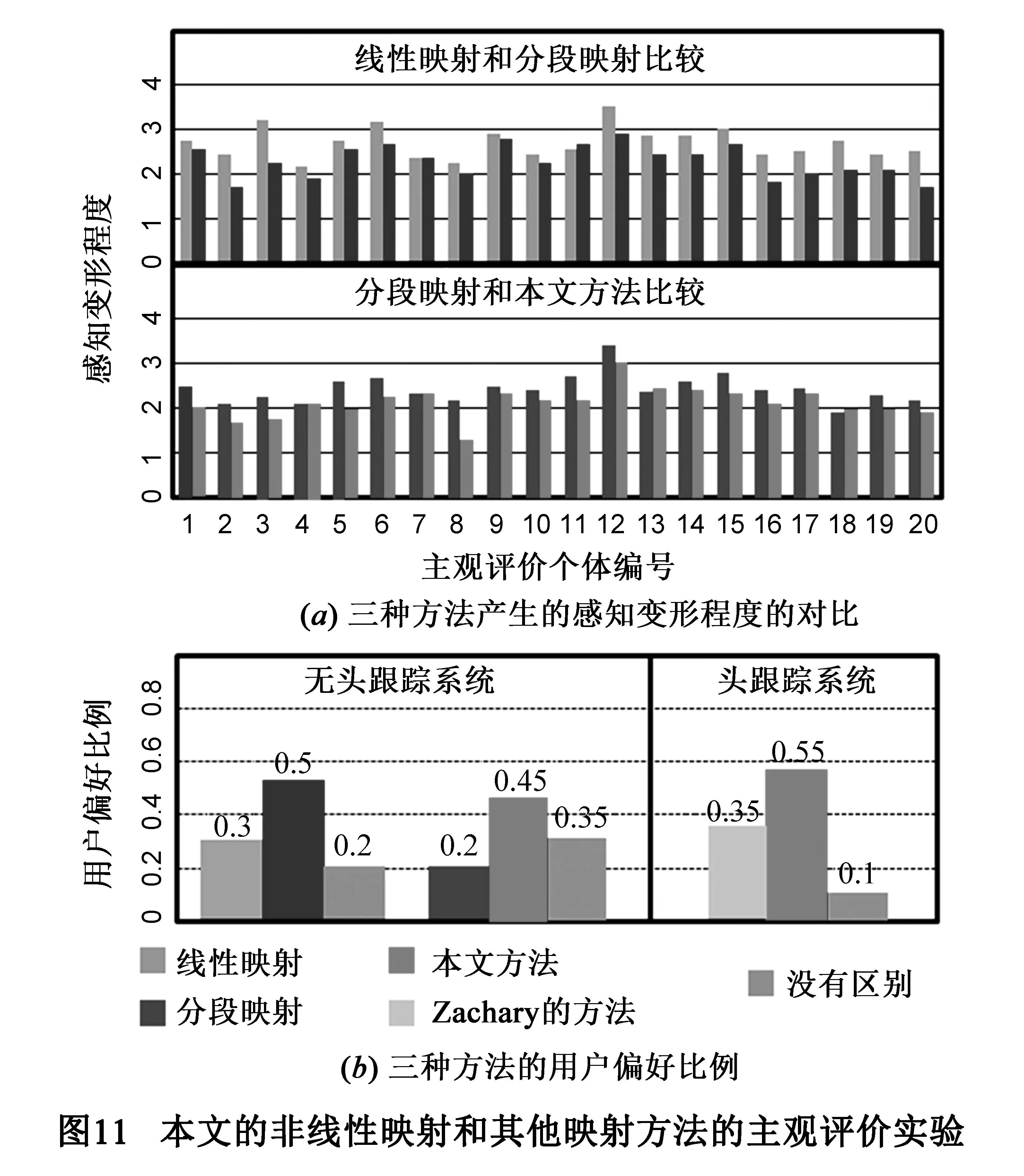
经过试验,我们筛选了二十个能正常观看立体图像的有效实验个体分别在无头跟踪和有头跟踪两种情况下对几种映射方法进行了主观评价实验.所有实验个体都来自在校学生,平均年龄21.3岁,其中男13人,女7人.

在无头跟踪虚拟现实系统中,我们采用了图10第一行和第二行图中的场景对线性映射、分段映射和本文的非线性映射进行了对比实验.为了避免因个体受试者的操作差异而产生的动态画面的不同,我们将场景动画渲染成3D视频.每个受试者分别就以下的两个方面进行评价.

(1) 对感知变形强度打分 (0～5分,分值越低感知变形越小).

(2) 你感觉哪个结果更好(选择一个或没有区别).

对比实验分两次进行,第一次分别对线性映射和分段映射进行比较,第二次对分段映射和本文方法进行比较.如图11所示：图11 (a)是对感知变形强度评价的两次实验数据.在头跟踪系统试验中,我们对本文方法和Zachary[16]提出消除图像漂移的线性映射方法和的进行了对比试验.图11 (b)的直方图表示了在有头跟踪和无头跟踪两种情况下,受试个体对几种方法主观偏好的比例.我们让受试者两侧的边缘之间来回移动4次,在观看两种方法的结果以后,对上面的第二个问题进行回答.由图11可以看出,在感知变形产生的视觉影响和观看者主观的偏好两方面,本文方法都优于线性映射和分段映射方法.

6 结论

本文针对虚拟现实系统,给出了头跟踪和无头跟踪两种情况下,双眼图像视差形成的几何分析.推导了双眼图像的投影矩阵.基于单相机拍摄的方法,我们讨论了模型变形和感知变形的关系,从而提出感知变形可以通过三维模型的网格变形来实现,并给出了利用模型变形来减小感知深度的方法.该方法可以实现平滑的非线性深度映射,如果应用于头跟踪系统中,还可以消除由于头部运动产生的图像漂移现象.实验证明本文给出的深度映射方法可以有效的减少因感知变形带来的视觉瑕疵.虽然我们是基于虚拟现实的应用而研究立体图像的生成,但本文方法也可以应用于虚拟场景的3D视频的渲染.

[1]Patterson R. Review paper-Human factors of stereo displays-An update[J]. Journal of the Society for Information Display,2009,17(12):987-996.

[2]侯春萍,袁万鑫,沈丽丽. 视差式立体信息采集、感知几何模型及舒适观看区研究综述[J].电子学报,2013,41(3):561-569. Hou C P,Yuan W X,Shen L L. The acquisition,perception geometric model and the comfortable viewing zone in stereoscopic video system:A review[J]. Acta Electronica Sinica,2013,41(3):561-569. (in Chinese)

[3]Oskam T,Hornung A,Bowles H,et al. OSCAM-Optimized stereoscopic camera control for interactive 3D [J]. Transactions on Graphics,2011,30(6):61-64.

[4]Heinzle S,Greisen P,Gallup D.Computational stereo camera system with programmable control loop[J].ACM Transaction on Graphics,2011,30(4):1-10.

[5]Zhang L,Vazquez C,Knorr S. 3D-TV content creation:Automatic 2D-to-3D video conversion [J]. IEEE Transactions on Broadcasting,2011,57(2):372-383.

[6]Ndjiki-Nya P,Koppel M,Doshkov D,et al. Depth image-based rendering with advanced texture synthesis for 3D video [J]. IEEE Transactions on Multimedia,2011,13(3):453-465.

[7]Sun W ,Au O C,Xu L,et al. Seamless view synthesis through texture optimization [J]. IEEE Transactions on Image Processing,2014,23(1):342-355.

[8]Yao C,Tillo T,Zhao Y,et al. Depth map driven hole filling algorithm exploiting temporal correlation information [J]. IEEE Transactions on Broadcasting,2014,60(2):394-404.

[9]Lang M,Hornung A,Wang O,et al. Nonlinear disparity mapping for stereoscopic 3D[J]. ACM Transactions,on Graphics,2010,29(4):157-166.

[10]Du S P,Hu S M,Ralph R. Martin changing perspective in stereoscopic images [J]. IEEE Transactions on Visualization & Computer Graphics,2013,19(8):1288-97.

[11]Lambooij M,Marten F,Ingrid H,et al. Visual discomfort and visual fatigue of stereoscopic displays-a review [J]. Journal of Imaging Science and Technology,2009,53(3):1-14.

[12]Mendiburu B. 3D Movie Making [M]. Burlington,USA:Elsevier Press,2009.

[13]Wopking M. Viewing comfort with stereoscopic pictures:an experimental study on the subjective effects of disparity magnitude and depth of focus [J]. Journal of the Society for Information Display,1995,3(3):101-103.

[14]Holliman N S. Smoothing region boundaries in variable depth mapping for real-time stereoscopic images [A]. Stereoscopic displays and virtual reality systems XII [C]. San Jose,USA:SPIE Press,2005. 281-292.

[15]Zilly F,Müller M,Eisert P,et al. The stereoscopic analyzer-an image-based assistance tool for stereo shooting and 3D production [A]. 17th IEEE International Conference on Image Processing [C].Los Alamitos:IEEE CPS,2010. 4029-4032.

[16]Zachary W,Larry F H,William R. Balancing fusion,image depth and distortion in stereoscopic head-tracked displays [A]. 1999 International Conference on Computer Graphics and Interactive Techniques (SIGGRAPH'99) [C].New York,USA:ACM Press,1999. 351-358.

[17]李大锦，白成杰. 实时立体视觉系统中的深度映射[J].中国图像图形学报，2015,20(3):366-373.

Li Dajin and Bai Chengjie. Depth mapping in real-time stereoscopic systems [J]. Journal of Image and Graphics,2015,20(3):366-373. (in Chinese)

[18]Shibata T,Kim J,Hoffman D M,et al. The zone of comfort:Predicting visual discomfort with stereo displays [J]. Journal of Vision,2011,11(8):74-76.

李大锦 男，1971年生于江苏省连云港，现为山东师范大学数字媒体系副教授，研究方向为计算机图形学，虚拟现实，计算机动画技术.

E-mail:ldjwqc@163.com

A Mesh-Warping-Based Method for Stereoscopic Images Generation in Virtual Reality System

LI Da-jin

(DigitalMediaDepartment,CommunicationSchool,ShandongNormalUniversity,Jinan,Shandong250014,China)

The paper introduced a novel method for stereoscopic image creation in virtual reality system.In this method,the left-and-right images were produced through different projection transformations in a single camera space,and the two types of projection matrices were derived respectively for stereoscopic head-tracked and non-head-tracked systems.Based on the single-camera method,we analyzed the relations among disparity,perceived depth,deformation of perceived objects and model mesh warping.The disparity and perceived deformation were modeled as 3D warping,so the disparity and the perceived deformation could be controlled by deforming the model mesh.Finally,a nonlinear perceived depth mapping method using mesh warping was proposed,which could reduce the artifacts caused by perceived distortion,and could avoid the image shift caused by perceived depth mapping in stereoscopic head-tracked system when the viewer moved his head left and right.

stereoscopic display;mesh warping;perceived deformation;depth mapping

2015-04-26；

2015-12-10；责任编辑：梅志强

国家自然科学基金(No.61340019)；山东省科技发展计划(No.2014GGH201004)；山东省重点研发计划 (No. 2015GGB01295)；山东自然科学基金(No.ZR2012FM029)

TP391

A

0372-2112 (2016)12-2946-08

��学报URL:http://www.ejournal.org.cn

10.3969/j.issn.0372-2112.2016.12.019