几类非确定型量子程序的终止验证
2017-01-10雷红轩彭家寅
雷红轩,彭家寅,刘 熠
(1.内江师范学院数学与信息科学学院,四川内江 641112; 2.四川省高等学校数值仿真重点实验室,四川内江 641112)
几类非确定型量子程序的终止验证
雷红轩1,2,彭家寅1,2,刘 熠1,2
(1.内江师范学院数学与信息科学学院,四川内江 641112; 2.四川省高等学校数值仿真重点实验室,四川内江 641112)
程序验证是保证程序正确性的关键技术.由于经典世界和量子世界的本质不同,经典程序验证的技术和工具不能直接应用到量子系统.而量子程序设计语言是描述量子系统的一种新的形式化模型,量子程序的验证问题就显得更为迫切和必要.本文首先讨论了量子通讯中常用的比特翻转、相位翻转、去极化、幅值阻尼、相位阻尼等信道作为特殊的非确定型量子程序从计算基态开始运行时的可达集合和终止集合等程序验证问题.其次,把上述五种量子程序两两组合组成非确定型量子程序,根据这五种量子程序的可达集合之相似点,最终合并成三种非确定型量子程序,重点讨论了这三种非确定型量子程序从计算基态开始运行时的终止和发散等程序验证问题.研究表明:这三种非确定型量子程序从计算基态0开始运行时都是终止的;而从计算基态1开始运行时:比特翻转信道和去极化信道组成的非确定型量子程序的终止和发散与分别刻画它们的两个参数有关;比特翻转信道和相位翻转信道组成的非确定型量子程序的终止和发散只与刻画比特翻转信道的参数有关;幅值阻尼信道和相位阻尼信道组成的非确定型量子程序是发散的,其发散条件与刻画量子信道的两个参数都没有关系.本文的结果可以为量子信息安全中量子通讯协议的验证提供理论和技术支持.
量子通讯;量子程序;程序验证;信息安全
1 引言
Shor[1]关于大数的质因子分解算法以及Grover[2]关于数据库搜索算法的相继出现,显示出量子计算在某些计算领域比经典计算更有效[3].当前,量子算法还处在较低水平的量子线路的探索阶段.正如Abramsky[4]所说的,高水平的概念化的方法对量子系统的设计、编程、推理是很必要的.正如此,在过去的20多年中,多种量子程序语言被先后定义和提出.比如,Knill[5]最先提出了设计量子程序语言,Ömer[6]第一次给出了真正的量子程序语言并对其进行了计算仿真,Selinger[7]指出一个量子程序由超算子描述.正确性是程序的最重要的属性之一.长期以来,如何保证程序的正确性、提高软件的可信度一直是计算机科学界高度关注的一个重要问题,也是推动计算机科学发展的主要动力之一.由于量子通讯协议可以由量子程序表示,所以量子程序的验证问题就显得更为迫切和必要.
同时,一些量子过程代数也被先后提出,如Gay和Nagarajan[8]提出了CQP代数,Feng等[9]提出了qCCS代数,这些代数系统为量子通讯和非确定型程序建立了良好的模型.最近,Li[10]等作者定义了一个语言独立的非确定型量子程序的模型,Yu[11]等作者提出了并发量子程序的概念和模型.在这些模型中,量子程序是由有限个量子队列组成的,这些量子队列是由状态空间上的量子Markov链描述.本文在上述工作和作者已有成果的基础上,首先讨论量子通讯中常用的比特翻转、相位翻转、去极化、幅值阻尼、相位阻尼等信道作为特殊的非确定型量子程序—确定型量子程序,从计算基态开始运行时的可达集合、终止集合、发散集合等情况.其次按照可达集合重点讨论这五种信道按照一定的组合方式组成的三种非确定型量子程序从计算基态开始运行时的终止和发散情况,进一步为量子程序和量子协议的验证提供理论和技术支持.
2 基本概念

定义1[10]设H是一个有限维Hilbert空间,它也是量子程序的状态空间.一个非确定型量子程序是二元组P=({εi|i=1,…,m},{M0,M1}),其中
(1)εi是H上的超算子,i=1,…,m;
(2){M0,M1}是H上的测量算子.
一个非确定型量子程序的一个计算是随机地选取m个超算子中的一个组成的有限或无限的计算序列,在整个计算过程中,测量算子{M0,M1}作用在每一步上,以决定程序是终止还是继续运行.这里选取“yes-no”测量,当测量结果为0时,程序终止,此时程序状态进入一个终止空间;否则,当测量结果为1时,程序将进入下一步,继续完成保迹的超算子ε.
程序P的执行表定义为集合
S={1,2,…,m}∞={s1s2…sk…|sk∈{1,2,…,m},k≥0}
(1)
程序P的有限执行表定义为集合
(2)
为方便起见,用θ表示空串.对任意的s=s1…sk∈Sfin,用|s|表示s的长度.对每一个|s|≤n,s(≤n)表示s的头部s1s2,…,sn,也写s=s1s2…∈S的头部为
s(≤n)=s1s2…sn∈Sfin
(3)
和尾部为
s(>n)=sn+1sn+2…∈S
(4)
为了简单表示,用Ti表示如下的超算子
(5)
其中,ρ∈D(H).进而,对任意的s=s1s2,…,sn∈Sfin,写
Ts=Tsn∘…∘Ts2∘Ts1
(6)
特别地,Tθ(ρ)=ρ.设ρ∈D(H)为输入态,程序P按照执行表s=s1s2,…,∈S执行,在n步后程序的状态为Ts(≤n)(ρ).
定义2[10]设非确定型量子程序的输入态为ρ,对任意一有限执行表s∈Sfin,定义程序P在s内终止的概率为
(7)
如果程序按照s=s1s2…执行,则程序在不超过n步终止的概率为ts(≤n)(ρ).进而,程序在有限步终止的概率为
(8)
显然,tr(ρ)≥ts(ρ),且tr(ρ)-ts(ρ)是程序在状态ρ运行执行表s时发散的概率.
对一个非确定型量子程序P,沿着任意一个执行表s∈S的执行都是可能的.因此,下面给出在所有可能的执行路径上程序终止概率的定义如下:
定义3[10]从状态ρ开始运行的非确定型量子程序P的终止概率定义为t(ρ)=inf{ts(ρ)|s∈S}.
定义4[10](1)开始于状态ρ的非确定型量子程序P的可达集合定义为R(ρ)={Ts(ρ)|s∈Sfin}.
(2)对任意的ρ∈D(H),如果t(ρ)=tr(ρ),则称ρ是程序P的终止状态,简称为终态.用T表示程序P的所有终态的集合,即T={ρ∈D(H)|t(ρ)=tr(ρ)}.
(3)对任意的ρ∈D(H),如果对某些s∈S,有ts(ρ)=0,则称ρ是P的发散态.用D表示程序P的所有发散态的集合,即D={ρ∈D(H)|ts(ρ)=0,对某些s∈S}.
等式t(ρ)=tr(ρ)被叫做非确定型量子程序P的终止条件.这个条件是说,只要程序P从状态ρ开始,则它一定会在有限步内终止且终止概率为1.
下面分别用I,X,Y,Z表示单位矩阵、Pauli-X矩阵、Pauli-Y矩阵、Pauli-Z矩阵.H2=span{|0〉,|1〉},M0=|0〉〈0|,M1=|1〉〈1|.
3 常用信道组成的确定型量子程序的可达集合和终态
为便于阅读,用Ei,i=1,…,5和εi,i=1,…,5分别表示比特翻转、相位翻转、去极化、幅值阻尼、相位阻尼等信道的运算元和Kraus算子和表示(超算子).
3.1 比特翻转信道组成的确定型量子程序的可达集合和终态
经计算P从计算基态|0〉或|1〉运行时的可达集合分别为R(|0〉〈0|)={|0〉〈0|,|1〉〈1|}和R(|1〉〈1|)={|0〉〈0|,|1〉〈1|},而|0〉,|1〉∈T,D=∅.
3.2 相位翻转信道组成的确定型量子程序的可达集合和终态

3.3 去极化信道组成的非确定型量子程序的可达集合和终态
经计算P从计算基态|0〉或|1〉运行时的可达集合均为R(|0〉〈0|)=R(|1〉〈1|)={|0〉〈0|,|1〉〈1|},而|0〉,|1〉∈T,D=∅.
3.4 幅值阻尼信道组成的确定型量子程序的可达集合和终态
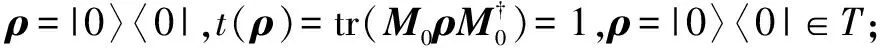
3.5 相位阻尼信道组成的确定型量子程序的可达集合和终态
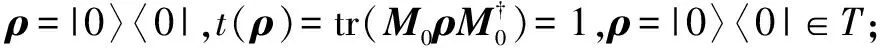
综上,在单量子比特空间H2中,五种确定型量子程序从计算基态|0〉或|1〉开始运行时有如下结论:
(1)比特翻转信道K1和去极化信道K3从{|0〉,|1〉}开始运行时的可达集合相同,即R(|0〉〈0|)=R(|1〉〈1|)={|0〉〈0|,|1〉〈1|},而|0〉,|1〉∈T,D=∅.
(2)相位翻转信道K2、幅值阻尼信道K4、相位阻尼信道K5从|0〉开始运行时的可达集合均为R(|0〉〈0|)={|0〉〈0|},且|0〉∈T;而从|1〉开始运行时的可达集合均为R(|1〉〈1|)={|1〉〈1|}且|1〉∈D,此时D≠∅.
4 几种常用量子信道组成的非确定型量子程序
由上一节的分析,下面我们根据这五种确定型量子程序的可达集合之相似点选取几种特殊的组合讨论这五种量子信道两两组合组成的非确定型量子程序从计算基态{|0〉,|1〉}开始运行时的终止和发散情况,即:
(1)比特翻转信道K1和去极化信道K3组成的非确定型量子程序;
(2)比特翻转信道K1和相位翻转信道K2组成的非确定型量子程序;
(3)幅值阻尼信道K4和相位阻尼信道K5组成的非确定型量子程序.
4.1 比特翻转信道和去极化信道组成的非确定型量子程序
比特翻转信道和去极化信道组成的非确定型量子程序为
P=({K1,K3},{M0,M1})
(9)
4.1.1K1执行m次后K3执行n次
(a)当ρ=|0〉〈0|时:Ts1(≤m)s3(≤n)(ρ)=0,t(ρ)=1,ρ∈T.即,非确定型量子程序P按执行表s=s1(≤m)s3(≤n)从初态|0〉〈0|运行时是终止的.
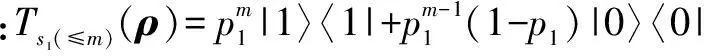
ts1(≤m)s3(≤n)(ρ)=
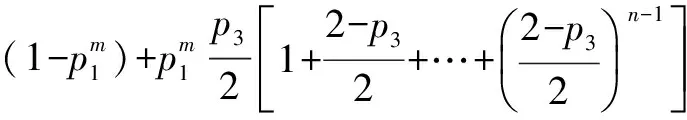
对终止概率t(ρ)的讨论如下:
(1)当p1=1,p3=0时:
ts1(≤m)s3(≤n)(ρ)=0
即ρ=|1〉〈1|∈D.
(2)当p1=0时:
ts1(≤m)s3(≤n)(ρ)=1
即ρ=|1〉〈1|∈T.
(3)p1=1,p3≠0时:
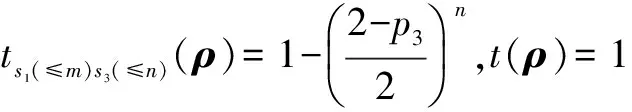
(4)p1≠1,p3≠0时:
即当m→∞,或n→∞,或m,n→∞时,t(ρ)=1.
(5)p1≠1,p3=1时:
即当m→∞,或n→∞,或m,n→∞时,t(ρ)=1.
(6)0 即当m→∞,或n→∞,或m,n→∞时,t(ρ)=1. (7)当p1≠1,p3=0时: 命题1 比特翻转信道(K1)和去极化信道(K3)组成的非确定型量子程序P按执行表s=s1(≤m)s3(≤n)运行时,有下列结论: (1)当初态为|0〉〈0|时是终止的; (2)当初态为|1〉〈1|,且当p1=1,p3=0时,ts(ρ)=0,即程序从状态|1〉〈1|开始运行时是发散的;否则,ts(ρ)=1,即程序从状态|1〉〈1|开始运行时是终止的. 4.1.2K3执行m次后K1执行n次 (a)当ρ=|0〉〈0|时: Ts3(≤m)s1(≤n)(ρ)=0,t(ρ)=1,ρ∈T 即,非确定型量子程序P按执行表s=s3(≤m)s1(≤n)从初态|0〉〈0|运行时是终止的. (b)当ρ=|1〉〈1|时: 则 ts3(≤m)s1(≤n)(ρ)= 对终止概率t(ρ)的讨论如下: (1)当p1=1,p3=0时: ts3(≤m)s1(≤n)(ρ)=0 即ρ=|1〉〈1|∈D. (2)当p1=0,p3≠0时: ts3(≤m)s1(≤n)(ρ)=1 即ρ=|1〉〈1|∈T. (3)当p1=0,p3=1时: ts3(≤m)s1(≤n)(ρ)=1,t(ρ)=1. (4)当p1=1,p3≠0时: (5)当p1≠1,p3=1时: ts3(≤m)s1(≤n)(ρ)=1,t(ρ)=1. (6)当p1=0,p3=0时: ts3(≤m)s1(≤n)(ρ)=1,t(ρ)=1. (7)当0 即当m→∞,或n→∞,或m,n→∞时,t(ρ)=1. 命题2 比特翻转信道(K1)和去极化信道(K3)组成的非确定型量子程序P按执行表s=s3(≤m)s1(≤n)运行时,有下列结论: (1)当初态为|0〉〈0|时是终止的; (2)当初态为|1〉〈1|,且当p1=1,p3=0时,ts(ρ)=0,即程序从状态|1〉〈1|开始运行时是发散的;否则,ts(ρ)=1,即程序从状态|1〉〈1|开始运行时是终止的. 4.1.3K1执行1次后K3执行1次如此反复 (a)当ρ=|0〉〈0|时:Ts1s3s1s3…(ρ)=0,t(ρ)=1,ρ∈T.即,非确定型量子程序P按执行表s=s1s3s1s3…从初态|0〉〈0|运行时是终止的. (b)初态ρ=|1〉〈1|: Ts(≤2n)(ρ)= ts(≤2n)(ρ)= 类似于命题1和命题2的讨论,有如下各结论. 命题3 比特翻转信道(K1)和去极化信道(K3)组成的非确定型量子程序P按执行表s=s1s3s1s3…运行时,有下列结论: (1)当初态为|0〉〈0|时是终止的; (2)当初态为|1〉〈1|,且当p1=1,p3=0时,ts(ρ)=0,即程序从状态|1〉〈1|开始运行时是发散的;否则,ts(ρ)=1,即程序从状态|1〉〈1|开始运行时是终止的. 4.1.4K3执行1次后K1执行1次如此反复 (a)当ρ=|0〉〈0|时:Ts3s1s3s1…(ρ)=0,t(ρ)=1,ρ∈T.即,非确定型量子程序P按执行表s=s3s1s3s1…从初态|0〉〈0|运行时是终止的. (b)初态ρ=|1〉〈1|: Ts(≤2n)(ρ)= ts(≤2n)(ρ)= 命题4 由比特翻转信道(K1)和去极化信道(K3)组成的非确定型量子程序P按执行表s=s3s1s3s1…运行时,有下列结论: (1)当初态为|0〉〈0|时是终止的; (2)当初态为|1〉〈1|,且当p1=1,p3=0时,ts(ρ)=0,即程序从状态|1〉〈1|开始运行时是发散的;否则,ts(ρ)=1,即程序从状态|1〉〈1|开始运行时是终止的. 综上可得如下定理: 定理1 设P是由比特翻转信道(K1)和去极化信道(K3)组成的非确定型量子程序,则P按任意的执行表s运行时,有如下结论: (1)当初态为|0〉〈0|时是终止的; (2)当初态为|1〉〈1|,且当p1=1,p3=0时,t(ρ)=0,即程序从状态|1〉〈1|开始运行时是发散的;否则,当p1≠1或p3≠0时,t(ρ)=1,即程序从状态|1〉〈1|开始运行时是终止的. 4.2 比特翻转信道和相位翻转信道组成的非确定型量子程序 比特翻转信道和相位翻转信道组成的非确定型量子程序为 P=({K1,K2},{M0,M1}) (10) 4.2.1K1执行m次后K2执行n次 (a)当初态ρ=|0〉〈0|时:Ts1(≤m)s2(≤n)(ρ)=0,t(ρ)=1,ρ∈T.即,非确定型量子程序P按执行表s=s1(≤m)s2(≤n)从初态|0〉〈0|运行时是终止的. 命题5 非确定型量子程序P按执行表s=s1(≤m)s2(≤n)运行时,有下列结论: (1)当初态为|0〉〈0|时是终止的; (2)当初态为|1〉〈1|,且当p1=0时,ts(ρ)=1,即程序从状态|1〉〈1|运行时是终止的;否则,当p1=1时,ts(ρ)=0,即程序从状态|1〉〈1|运行时是发散的. 4.2.2K2执行m次后K1执行n次 (a)当初态ρ=|0〉〈0|时:Ts2(≤m)s1(≤n)(ρ)=0,t(ρ)=1,ρ∈T.即,非确定型量子程序P按执行表s=s2(≤m)s1(≤n)从初态|0〉〈0|运行时是终止的. (b)当初态ρ=|1〉〈1|: 命题6 非确定型量子程序P按执行表s=s2(≤m)s1(≤n)运行时,有下列结论: (1)当初态为|0〉〈0|时是终止的; (2)当初态为|1〉〈1|,且当p1=0时,ts(ρ)=1,即程序从状态|1〉〈1|运行时是终止的;否则,当p1=1时,ts(ρ)=0,即程序从状态|1〉〈1|运行时是发散的. 4.2.3K1执行1次后K2执行1次如此反复 (a)当初态ρ=|0〉〈0|时:Ts1s2s1s2…(ρ)=0,t(ρ)=1,ρ∈T.即,非确定型量子程序P按执行表s=s2s1s2s1…从初态|0〉〈0|运行时是终止的. (b)当初态ρ=|1〉〈1|时: 命题7 非确定型量子程序P按执行表s=s1s2s1s2…运行时,有下列结论: (1)当初态为|0〉〈0|时是终止的; (2)当初态为|1〉〈1|,同时当p1=0时,ts(ρ)=1,即程序从状态|1〉〈1|运行时是终止的;否则,当p1=1时,ts(ρ)=0,即程序从状态|1〉〈1|运行时是发散的. 4.2.4K2执行1次后K1执行1次如此反复 (a)当初态ρ=|0〉〈0|时:Ts2s1s2s1…(ρ)=0,t(ρ)=1,ρ∈T.即,非确定型量子程序P按执行表s=s2s1s2s1…从初态|0〉〈0|运行时是终止的. (b)当初态ρ=|1〉〈1|时: 命题8 非确定型量子程序P按执行表s=s2s1s2s1…运行时,有下列结论: (1)当初态为|0〉〈0|时是终止的; (2)当初态为|1〉〈1|,且当p1=0时,ts(ρ)=1,即程序从状态|1〉〈1|运行时是终止的;否则,当p1=1时,ts(ρ)=0,即程序从状态|1〉〈1|运行时是发散的. 定理2 设P是由比特翻转信道(K1)和相位翻转信道(K2)组成的非确定型量子程序,则程序P按任意执行表s运行时,有下列结论: (1)当初态为|0〉〈0|时是终止的; (2)当初态为|1〉〈1|,且当p1=0时,t(ρ)=1,即程序从状态|1〉〈1|运行时是终止的;否则,当p1=1时,t(ρ)=0,即程序从状态|1〉〈1|运行时是发散的; (3)当初态为|1〉〈1|时,程序P的终止和发散只与比特翻转信道(K1)的参数p1有关. 从上面的定理可以看到,比特翻转信道(K1)和相位翻转信道(K2)组成的非确定型量子程序P的终止和发散只与比特翻转信道(K1)的参数p1有关,与相位翻转信道(K2)的参数p2没有关系,这和比特翻转信道(K1)单独作为确定型量子程序时终止和发散的结论一致. 4.3 幅值阻尼信道和相位阻尼信道组成的非确定型量子程序 幅值阻尼信道和相位阻尼信道组成的非确定型量子程序为 P=({K4,K5},{M0,M1}) (11) 分别选取执行表s为s′=s4(≤m)s5(≤n),s″=s5(≤m)s4(≤n),s‴=s4s5s4s5…,s″=s5s4s5s4…经计算均有如下的结果: (a)当初态ρ=|0〉〈0|时:Ts(ρ)=0,t(ρ)=1,ρ∈T.即,非确定型量子程序P按执行表s从初态|0〉〈0|运行时是终止的. (b)当初态ρ=|1〉〈1|时: Ts(ρ)=(1-p4)l|1〉〈1|,t(ρ)=0,ρ∈D, 其中l为幅值阻尼信道K4执行的次数. 定理3 设P是由幅值阻尼信道(K4)和相位阻尼信道(K5)组成的非确定型量子程序,则程序P按任意执行表s运行时,有下列结论: (1)当初态为|0〉〈0|时是终止的; (2)当初态为|1〉〈1|,t(ρ)=0,即程序从状态|1〉〈1|开始运行时是发散的. 终止条件是研究循环程序的一个非常重要但又极其困难的课题.事实上一般量子循环的终止是不可判定的.本文对几类非确定型量子程序的终止和发散进行了详细的讨论,此研究对量子程序的设计和量子协议的设计都有很好的帮助和启迪作用,但对非确定型量子程序的研究还有很多的理论和实验需要完善和补充,例如对于五种常用量子信道两两组成的非确定型量子程序在别的测量算子,如M0=|+〉〈+|,M1=|-〉〈-|下的终止和发散情况,及H2空间中两个以上常用量子信道组合组成的非确定型量子程序的终止发散的情况如何我们在另文中加以讨论. [1]P W Shor.Algorithms for quantum computation:discrete logarithms and factoring[A].Proc.35th Annual Symp.on Foundations of Computer Science[C].Los Alamitos,CA:IEEE Press,1994.124-134. [2]L Grover.A fast quantum mechanical algorithm for database search[A].Proc 28th Annual ACM Symp on the Theory of Computing[C].New York:ACM Press,1996.212-219. [3]M A Nielsen,I L C′huang.Quantum Computation and Quantum Information[M].Cambridge:Cambridge University Press,2000. [4]S Abramsky.High-level methods for quantum computation and information[A].Proceedings of the 19th Annual IEEE Symposium on Logic in Computer Science (LICS'04)[C].USA:IEEE Computer Society,2004.410-414. [5]E H Knill.Conventions for Quantum Pseudocode[R].USA:Los Alamos National Laboratory,1996. [6]Bömer.A Procedural Formalism for Quantum Computing[D].Vienna:Department of Theoretical Physics,Technical University of Vienna,1998. [7]P Selinger.Towards a quantum programming language[J].Mathematics Structures in Computer Science,2004,14(4):527-586. [8]S J Gay,R Nagarajan.Communicating quantum processes,annual symposium on principles of programming languages[A].Proceedings of the 32nd ACM SIGPLAN-SIGACT symposium on Principles of programming languages[C].USA:Programming Language,2005.145-157. [9]Y Feng,R Y Duan,M S Ying.Bisimulation for quantum processes[A].Proceedings of the 38th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages (POPL)[C].New York:ACM Press,2011.523-534. [10]Y J Li,N K Yu,M S Ying.Termination of nodeterministic quantum programs[J].Acta Informatica,2014,51(1):1-24. [11]N K Yu,M S Ying.Reachability and termination analysis of concurrent quantum programs[J].Lecture Notes in Computer Science,2012,7454:69-83. [12]M S Ying,N K Yu,Y Feng,R Y Duan.Verification of quantum programs[J].Sci Comput Program,2013,78(9):1679-1700. [13]雷红轩,席政军,李永明.广义量子Loop程序的若干性质[J].电子学报,2013,41(4):727-732. LEI Hong-xuan,XI Zheng-jun,LI Yong-ming.Some properties of genaralized quantum loop program[J].Acta Electronica Sinica,2013,41(4):727-732.(in Chinese) [14]雷红轩,席政军,李永明.量子最弱自由前置条件的交换性及其性质[J].软件学报,2013,24(5):933-941. LEI Hong-xuan,XI Zheng-jun,LI Yong-ming.Commutativity of quantum weakest liberal precondition and its properties[J].Journal of Software,2013,24(5):933-941.(in Chinese) [15]林运国,雷红轩,李永明.量子马尔可夫链安全性模型检测[J].电子学报,2014,42(11):2191-2197. LIN Yun-guo,LEI Hong-xuan,LI Yong-ming.Model checking of safety property over quantum markov chain[J].Acta Electronica Sinica,2014,42(11):2191-2197.(in Chinese) 雷红轩 男,1967年出生于陕西洋县,博士,教授,主要研究领域为自动机理论,量子程序验证和量子模型检测. E-mail:hongxuan-lei@163.com 彭家寅 男,1962出生于四川资中县,博士,教授,主要研究领域为量子信息处理. E-mail:pengjiayin62226@163.com 刘 熠 男,1979年出生于四川仪陇县,博士,副教授,主要研究领域为智能信息处理. E-mail:liuyiyl@126.com Termination Verification of Some Kinks Nondeterministic Quantum Programs LEI Hong-xuan1,2,PENG Jia-yin1,2,LIU Yi1,2 (1.SchoolofMathematicsandInformationScienceofNeijiangNormalUniversity,Neijiang,Sichuan641112,China; 2.KeyLaboratoryofNumericalSimulationofSichuanProvince,Neijiang,Sichuan641112,China) Program verification is the key technology to ensure the correctness of the program.However,due to essential differences of the classical and quantum world,classical program verification techniques and tools cannot be applied directly to the quantum system.Since quantum programming language is a new formal model of quantum system,the verification problem of quantum program is more urgent and necessary.We investigate the program verification for the reachable set and the terminating set of specific nondeterministic quantum program described respectively by bit flip channel,phase flip channel,depolarizing channel,amplitude damping channel and phase damping channel starting from computational basic states in quantum communication systems.Then,we combine pairwise the above five quantum programs into nondeterministic quantum programs,and merge these nondeterministic quantum programs into three nondeterministic quantum programs in terms of the similarities of the reachable set of five quantum programs,and discuss the problem for termination and divergence of these three nondeterministic quantum programs starting from computational basic states.The results shows that these three nondeterministic quantum programs starting from computational basic state 0 are terminated,while starting from computational basic state 1,the termination and the divergence of nondeterministic quantum program consisted by bit flip channel and depolarizing channel relates to the two parameters describing two quantum channels,the termination and the divergence of nondeterministic quantum program consisted by bit flip channel and phase flip channel relates to one parameter describing bit flip channel,and nondeterministic quantum program consisted by amplitude damping channel and phase damping channel is divergence without the two parameters describing quantum channel.And the results provide theoretical and technical support for verification of quantum communication protocol in quantum information security. quantum communication;quantum programs;program verification;information security 2015-07-06; 2015-11-06;责任编辑:覃怀银 四川省教育厅重点科研项目(No.14ZA0242);教育部数学与应用数学专业综合改革(No.ZG0464);四川省数学与应用数学专业综合改革(No.01249);四川省教育厅科研创新团队基金(No.15TD0027);四川省应用基础研究计划(No.2015JY0120) TP301.6 A 0372-2112 (2016)12-2932-07 ��学报URL:http://www.ejournal.org.cn 10.3969/j.issn.0372-2112.2016.12.017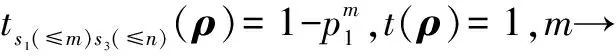
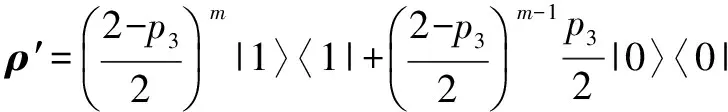
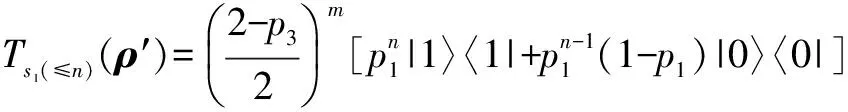
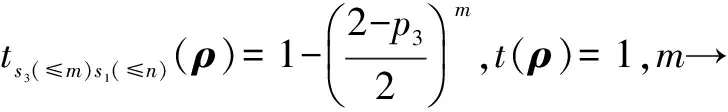
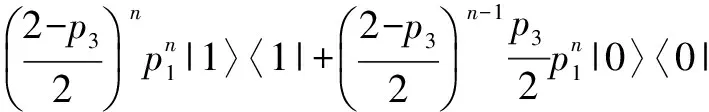
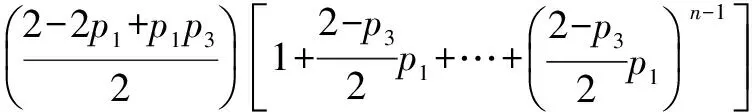

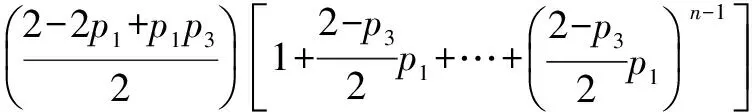
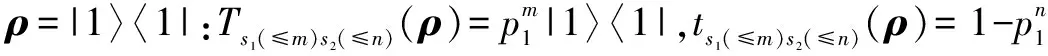
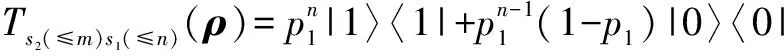

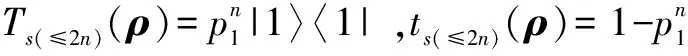
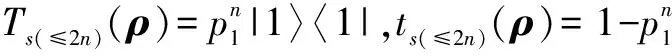
5 结束语



