改进的复合光栅投影快速三维测量方法

杨丽娟， 束益梅， 程 菊,2, 边心田,2

(1.淮阴师范学院 物理与电子电气工程学院, 江苏 淮安 223300; 2.淮阴师范学院 江苏省现代检测技术与智能系统重点建设实验室, 江苏 淮安 223300)



改进的复合光栅投影快速三维测量方法

杨丽娟1， 束益梅1， 程 菊1,2, 边心田1,2

(1.淮阴师范学院 物理与电子电气工程学院, 江苏 淮安 223300; 2.淮阴师范学院 江苏省现代检测技术与智能系统重点建设实验室, 江苏 淮安 223300)

提出一种新相移算法下的复合光栅投影三维测量方法．利用逆推法建立投影光栅模型,对投影仪投出的光栅进行预校正,保证投到参考面的条纹为标准的正弦分布．测量过程由具有相移的复合光栅到待测物体表面,CCD相机采集变形条纹图,将采集到的图像分离成3帧单色图,再由相位算法提取相位,通过高度映射公式恢复待测物体的三维面形．该方法有较好的抗噪性能,为动态在线测量奠定了基础．计算机仿真实验验证了该方法的可行性．

三维测量; 复合光栅; 逆推法; 光栅投影

0 引言

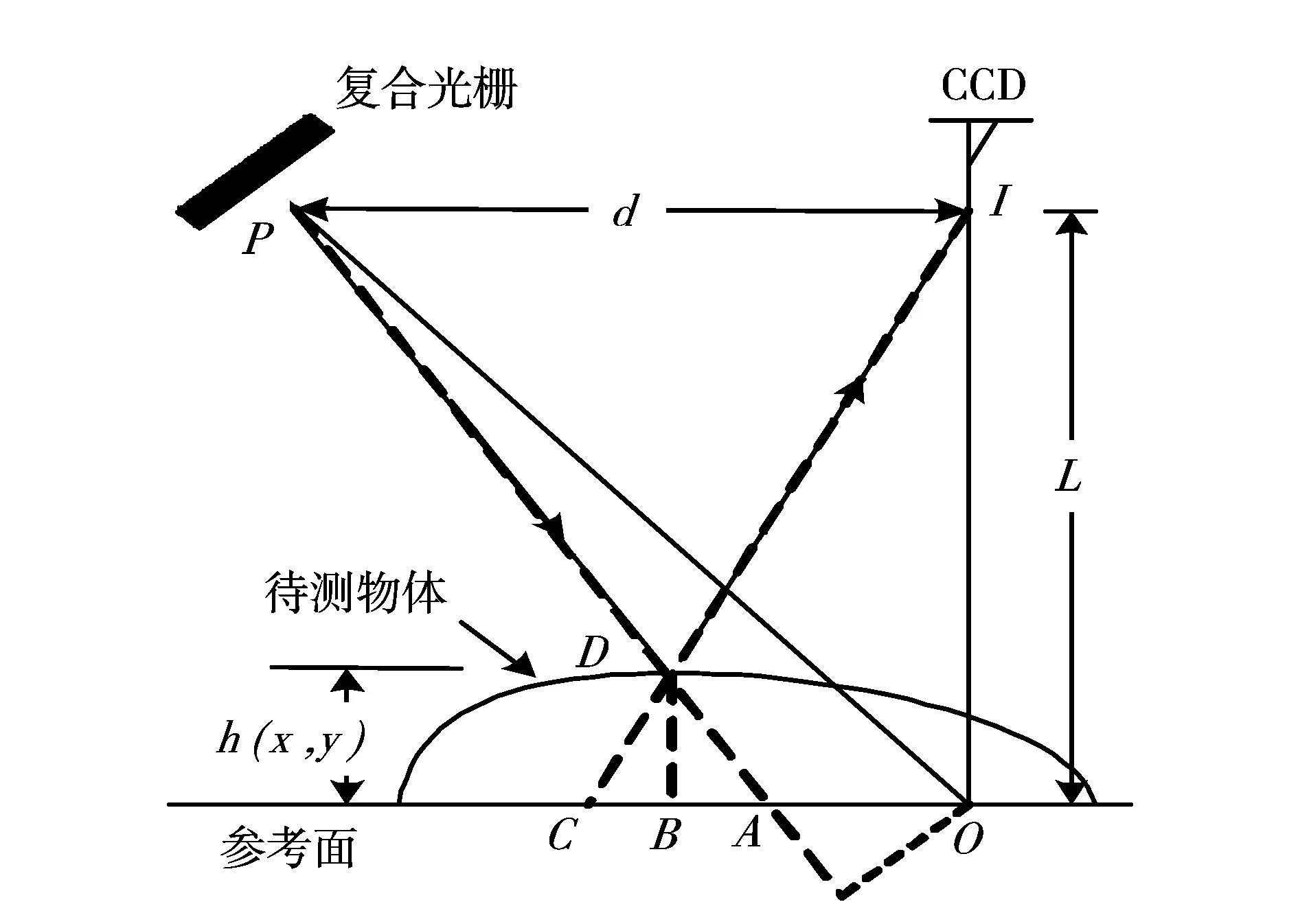
图1 系统测量原理示意图

1 测量原理

1.1 光栅模型

通常采用发散光路投影的测量系统原理如图1所示,投影到参考面的条纹会产生畸变,其几何变换关系[9]为

(1)

式中,x,x′分别为投影光栅上点的坐标和与之对应的投影到参考面上点的坐标,d是投影系统出瞳与成像系统入瞳之间的距离,L是成像系统入瞳与参考面之间的距离,f是投影系统焦距．投影到参考面上的条纹是等周期分布的,令其周期为p,其相位分布φ(x)可表示为

(2)

所以,投影光栅的相位分布函数为

(3)

1.2 相位分析

I(x,y)= Rr(x,y){Ar(x,y)+Br(x,y)cosφ(x,y)}+

(4)

Ir(x,y)=Rr(x,y){Ar(x,y)+Br(x,y)cosφ(x,y)}

(5)

(6)

(7)

联立式(5)～(7),计算出相位分布为

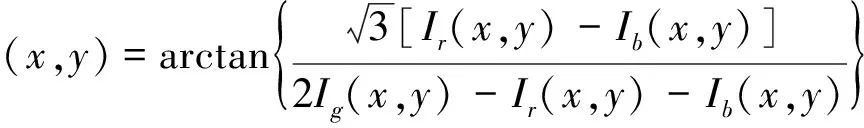
(8)

由式(8)计算出的相位分布被截断在反三角函数的主值范围内,必须展开成连续的相位φu．所以,物体的相位-高度之间的关系[1]可以表示为

(9)

2 计算机模拟

为了验证提出方法的可行性,进行了计算机仿真实验．模拟待测物体大小为400×400 pixel,高度为4 cm的Peaks函数,如图2所示．利用提出方法将一幅复合光栅图像投影到被测物体上,对成像系统获取的变形条纹如图3所示,并对其进行分离成3帧具有相移的单色变形条纹图像如图4,利用式(8)求出物体的相位,最后根据相位-高度映射关系恢复物体的三维面形如图5所示．在条纹图中给强度添加了3%的随机噪声后恢复物体与实际待测物体的误差如图6所示．由图6可以看出,本文提出的方法具有较高的测量精度,可以将误差控制在0.02 μm以内．

图2 模拟待测物体图像 图3 变形条纹图像

图4 通过变形条纹图分离成3帧具有相移的单色变形条纹图像

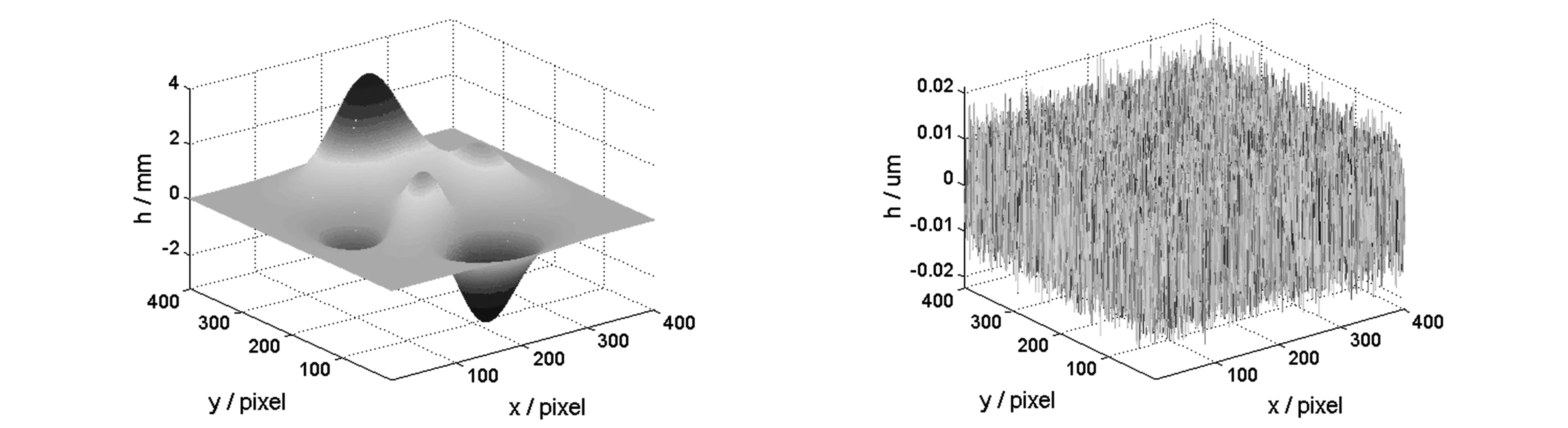
图5 恢复物体图像 图6 恢复物体与待测物体的误差

3 结论

提出光栅预校正与复合光栅相结合的方法．将复合光栅投影的彩色条纹图分离成具有相移的RGB单色条纹强度分布图,有效的避免了传统算法中相移误差的问题,提高了测量精度;光栅预校正算法简化了测量过程．提出方法具有较强的抗噪声能力,在较大噪声情况下,仍能获得满意的效果,仿真实验验证了本方法的可行性,为在线三维测量提供了一种有效的测量手段．

[1] 苏显渝. 信息光学[M].北京:科学出版社,2011.

[2] 陈锋,萝莉. 复合光栅投影的相位测量轮廓术[J]. 激光杂志,2007, 28(3): 52-53.

[3] 李华伟,申作春,覃银红,等. 相位测量轮廓术应用于叶片测量[J]. 航空动力学报,2012,27(2):275-281.

[4] Liu Y K, Su X Y, Zhang Q C. A novel encoded-phase technique for phase measuring profilometry[J]. Optics express, 2011, 19(15): 14137-14144.

[5] 盖绍彦,达飞鹏.基于数字投影仪的光栅相位自校正方法[J].自动化学报,2008,34(11): 1364-1366.

[6] Zhang S, Yau S T. Absolute phase-assisted three-dimensional data registration for a dual-camera structured light system[J]. Applied Optics, 2008, 47(17):3134-3142.

[7] Su W H. Color-encoded fringe projection for 3D shape measurements[J]. Optics Express, 2007, 15(20): 13167-13181.

[8] 刘玉凤,曹益平,何宇航. 新改进型三步非等步相位测量轮廓术算法[J].光电子·激光, 2010, 21(1): 83-86.

[9] 马云秀,边心田. 相位测量轮廓术中投影条纹畸变的研究[J]. 光电技术应用,2013, 28(4):83-85.

[责任编辑：蒋海龙]

Modified Phase Measuring Profilometry based on Color-encoded Fringe Projection

YANG LI-juan1, SHU Yi-mei1, CHENG Ju1,2, BIAN Xin-tian1,2

(1.School of Physics and Electronic and Electrical Engineering, Huaiyin Normal University, Huaian Jiangsu 223300, China)(2.Jiangsu Key Construction Laboratory of Modern Measurement Technology and Intelligent System, Huaiyin Normal University, Huaian Jiangsu 223300, China)

A new method for 3D measurement of color-encoded grating projection based on a new phase shifting algorithm is presented. First of all, the inverse-deducing method is used to set up the grating model for projection. Then, according to the established model, the projected grating can be pre-corrected in order to ensure that the intensity of the stripe projected on the reference surface is up to a standard sinusoidal distribution. When measuring, after projecting the compound grating with phase shifting to the object, the deformed fringe which can be separated to three monochromatic images is captured by CCD, and then, the phase distribution will be extracted so as to recover three-dimensional shape of the object according to the height mapping formula. This proposed method has strong noise resistance and shows high performance in case of adding great noise to the image, which is much helpful for dynamic online measurement. The feasibility of the method is verified by computer simulation experiment.

3D measurement; color-encoded grating; inverse-deducing method; grating projection

2016-06-22

江苏省高校大学生创新创业训练计划项目(201510323018Z); 淮安市科技支撑计划项目(HAG2014019)

边心田(1978-)，男，山东淄博人，副教授，博士，主要研究方向为光学三维传感与机器视觉. E-mail: bianxt@126.com

O438

A

1671-6876(2016)04-0305-04