多机系统励磁与SSSC的非线性鲁棒协调控制
2017-01-10刘青张立娜陈世超
刘青,张立娜,陈世超
(华北电力大学电气与电子工程学院,河北省保定市 071003)
多机系统励磁与SSSC的非线性鲁棒协调控制
刘青,张立娜,陈世超
(华北电力大学电气与电子工程学院,河北省保定市 071003)
针对多机电力系统中,发电机励磁和静止同步串联补偿器(static synchronous series compensator,SSSC)的协调控制问题,引入广义Hamilton系统理论,进行非线性协调控制器设计。SSSC采用考虑内部动态的三阶模型,并将SSSC与各台发电机的相互作用用附加电磁功率表示。将包含发电机励磁和SSSC的多机电力系统描述成广义耗散Hamilton系统形式,利用边界函数法和L2干扰抑制控制方法设计了发电机励磁和SSSC的协调控制器。四机两区域系统的仿真结果表明:与传统的分散控制器相比,所提的非线性协调控制器能够有效地提高系统的暂态稳定性和电压调节性能。
发电机励磁;静止同步串联补偿器(SSSC);广义Hamilton系统理论;非线性鲁棒协调控制
0 引 言
静止同步串联补偿器(static synchronous series compensator, SSSC)是柔性交流输电系统(flexible alternative current transmission systems,FACTS)的重要设备之一,它能够连续地调节线路的电抗,从而控制线路的传输功率[1-2]。由于其良好的动态特性和可控性,在抑制系统区域间低频振荡、提高系统输送能力和系统暂态稳定性方面发挥着重要作用[3-4]。国内外学者在SSSC控制器设计及其与发电机励磁的协调控制方面取得了一定的研究成果。文献[5]建立了含SSSC的修正Phillips-Heffron模型,并根据最优控制理论设计了SSSC和发电机励磁的协调控制器。文献[6]将直接反馈线性化方法首次应用到SSSC和发电机励磁的协调控制上,提高了系统的暂态稳定性。文献[7]建立了SSSC的五阶数学模型,利用状态-动态-量测(state dynamic measurement,SDM)反馈线性H控制方法设计了单机无穷大系统中SSSC的鲁棒控制器。上述文献中所用到的控制理论和方法都依赖于系统确定的线性化数学模型。然而,电力系统是强非线性动态系统,故应用非线性控制理论设计系统的稳定控制器是十分必要的。
近年来,Hamilton系统理论受到非线性系统控制领域的广泛关注。Hamilton系统理论能有效地利用系统的内部结构特性,使得基于此理论设计的控制器具有较好的动态特性和稳定性能[8]。文献[9]基于连接阻尼配置—无源控制方法,完成了考虑转移电导的受控多机电力系统的Hamilton实现。文献[10]提出了伪广义Hamilton理论,并将其应用于发电机励磁控制当中。文献[11]通过预置反馈方法完成广义拟Hamilton实现,提出了一种适用于此系统的镇定控制器的设计方法,并据此设计了多个静止无功补偿器(static var compensator,SVC)的协调控制策略。
本文基于广义Hamilton理论,对多机系统发电机励磁和SSSC装置同时进行协调控制。SSSC采用考虑内部动态的三阶模型,并将SSSC对系统的调节作用融入到发电机电磁功率的表达式中。将包含发电机励磁和SSSC的多机电力系统描述成广义耗散Hamilton系统形式,构造此系统的Hamilton能量函数,再利用边界函数法和L2干扰抑制控制方法,得到发电机励磁和SSSC的协调控制策略。仿真算例表明本文所设计的非线性协调控制器具有良好的控制效果。
1 广义Hamilton系统的扩展L2干扰抑制控制理论
对于包含扰动项的仿射非线性系统,有
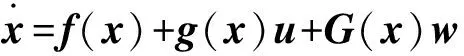
(1)
式中:f(x)∈Cr(Rn)为n维微分流形;g(x)、G(x)分别为适当阶数的控制项和扰动项系数矩阵;x∈Rn、u∈Rm和w∈Rs分别为系统的状态变量、控制输入向量和扰动项。若存在一个有界函数H(x),可将系统(1)表示成如式(2)所示的形式:
(2)
式中∑(x)在系统的平衡点x0处为0,并且在x的定义域空间中一致有界,其他变量的定义可参考文献[12]。利用边界函数方法[13],假设存在一个正定函数ρ(x)可以使式(3)成立,即
(3)
如果公式(2)满足系统是零状态可检的,并且Hamilton函数H(x)在平衡点处存在局部最小值,则存在定理1。

(4)
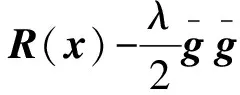
2 SSSC的动态模型和多机电力系统广义耗散Hamilton实现
考虑一个含有n台发电机,m个负荷节点和一台SSSC的电力系统模型,SSSC装置安装于母线n+1和n+2之间。
2.1 SSSC的动态模型
SSSC的等效电路如图1所示,在dq坐标系中,SSSC的三阶非线性动态方程[15]如式(5)所示。

图1 SSSC的等效电路结构图
图1中:Udc表示直流侧电容电压;Idc表示直流侧电容输出电流;Rs和Ls分别为耦合变压器的等效电阻和漏电感;Cdc表示直流侧电容器的电容;Pse和Qse分别表示SSSC注入系统的有功功率和无功功率;Rdc表示换流器的切换损失;ia、ib和ic分别表示SSSC注入系统的三相电流;Un+1∠θn+1和Un+2∠θn+2表示SSSC接入母线的电压。
(5)
式中:id和iq分别为SSSC注入系统的d轴和q轴电流;ωs表示系统角频率;w3和w4分别为SSSC的等效输入扰动。式中除ωs为有名值外,其余变量均为标幺值。
控制输入变量ud和uq的表达式如式(6)所示:
(6)
式中:m和δ分别为换流器的调制比和相位移。
Ud1、Uq1、Ud2和Uq2的表达式如式(7)—(8)所示:
(7)
(8)
2.2 多机电力系统的广义耗散Hamilton实现
SSSC接入电力系统后会对发电机输出的电磁功率和d轴电流产生影响,定义为ΔPei和ΔIdi。发电机采用三阶实用模型,则n机电力系统中第i台发电机的动态方程如式(9)所示:

(9)
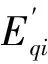
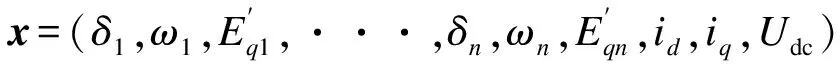
(10)
(11)
考虑SSSC的动态调节作用,构造多机系统的Hamilton函数如式(12)所示:
(12)
构造的函数H(x)为包含SSSC装置附加势能在内的系统的总能量,并且该函数反映了发生扰动后系统能量的转移过程。
计算能量函数H(x)对各个状态变量的偏导数,则多机系统的动态方程可表示为
(13)
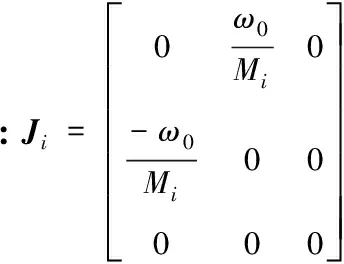



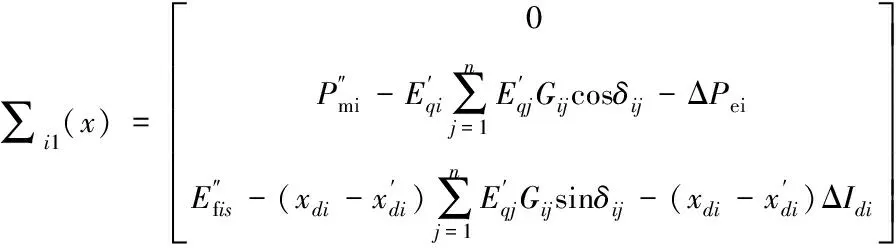
u1i=ufi;u2=[ud-ud0,uq-uq0]T;ud0、uq0分别为平衡状态下SSSC的初始控制量值。
3 发电机励磁和SSSC的协调控制器设计
要想利用定理1设计相应的控制器,则如式(13)所示的系统必须满足第1部分所述扩展L2干扰抑制控制理论的条件。
(1)显而易见,当u=0时,系统是零状态可检的。
(2)由Hamilton函数的表达式易知其在系统平衡点x0处的值H(x0)=0,且∂xH(x)|x=x0=0。复杂多机电力系统很难用解析表达式给出Hessian矩阵的正定条件,但可用计算机数值计算方法判断其Hessian矩阵的正定性,或者得到其正定条件[6]。若H(x)的Hessian矩阵正定,则此时函数H(x)在平衡点处存在局部最小值。
(3)由∑(x)的表达式可知∑(x)在系统的平衡点x0处为0,并且在x的定义域空间中一致有界。
(14)
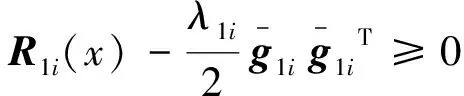
(15)
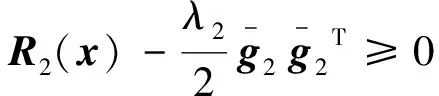
(16)
(17)
(18)
故可以根据定理1设计发电机励磁和SSSC的非线性协调控制策略。根据公式(4)可得多机系统中第i台发电机励磁的控制策略,如式(19)所示:
(19)
SSSC装置的控制策略如式(20)—(21)所示:
(20)
(21)
从发电机励磁控制策略的表达式(19)可知,发电机励磁控制不仅需要本地的测量信号,还需要系统中其余发电机的广域控制信息。同步相量测量装置(phasor measurement unit, PMU)和电网广域监测系统(wide area measurement system, WAMS)的快速发展为电网中主要数据的实时高速率采集提供了有效的技术支撑。
4 仿真分析
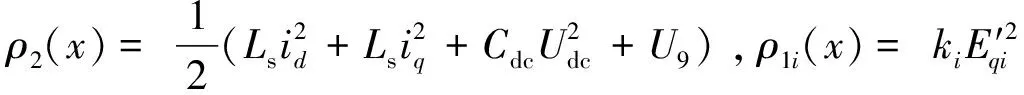
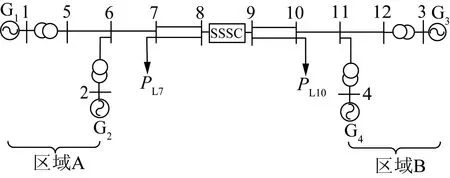
图2 四机两区域系统结构图
为充分验证本文所设计的发电机励磁和SSSC的非线性协调控制器的有效性,选取以下2种故障情况将协调控制器仿真效果与分散控制进行对比分析。
(1)设定在母线9处2.0 s时发生瞬时三相接地故障,0.1 s后故障消失,系统的动态响应曲线如图3—5所示。
(2)设定在线路9—10之间2.0 s时发生瞬时单相接地故障,0.1 s后故障消失,系统的动态响应曲线如图6—8所示。
从图3—8可以看出:系统无论发生瞬时性三相故障还是单相故障后,与分散控制器相比,本文所设计的非线性协调控制器能够更快速地使系统恢复到稳定运行的状态。在暂态过程中发电机的功角差和联络线功率的超调量都比较小,并且对短路电压也具有一定的支撑作用,提高了系统的暂态稳定性和动态性能。

图3 G1和G3的功角差Δδ13的响应曲线(故障1)

图4 联络线传输功率P7-8的响应曲线(故障1)
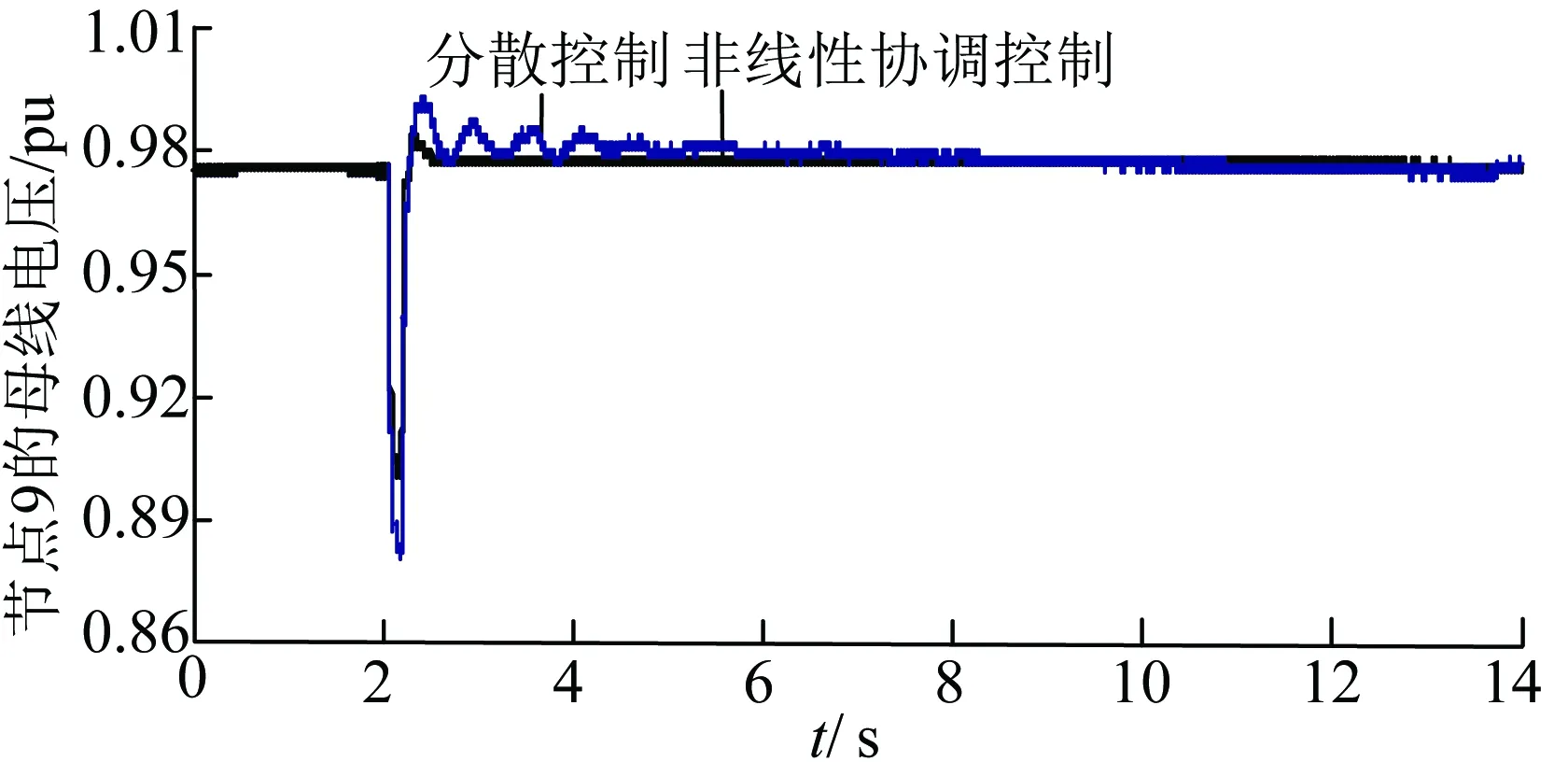
图5 母线9电压的响应曲线(故障1)

图6 G1和G3的功角差Δδ13的响应曲线(故障2)

图7 联络线传输功率P7-8的响应曲线(故障2)
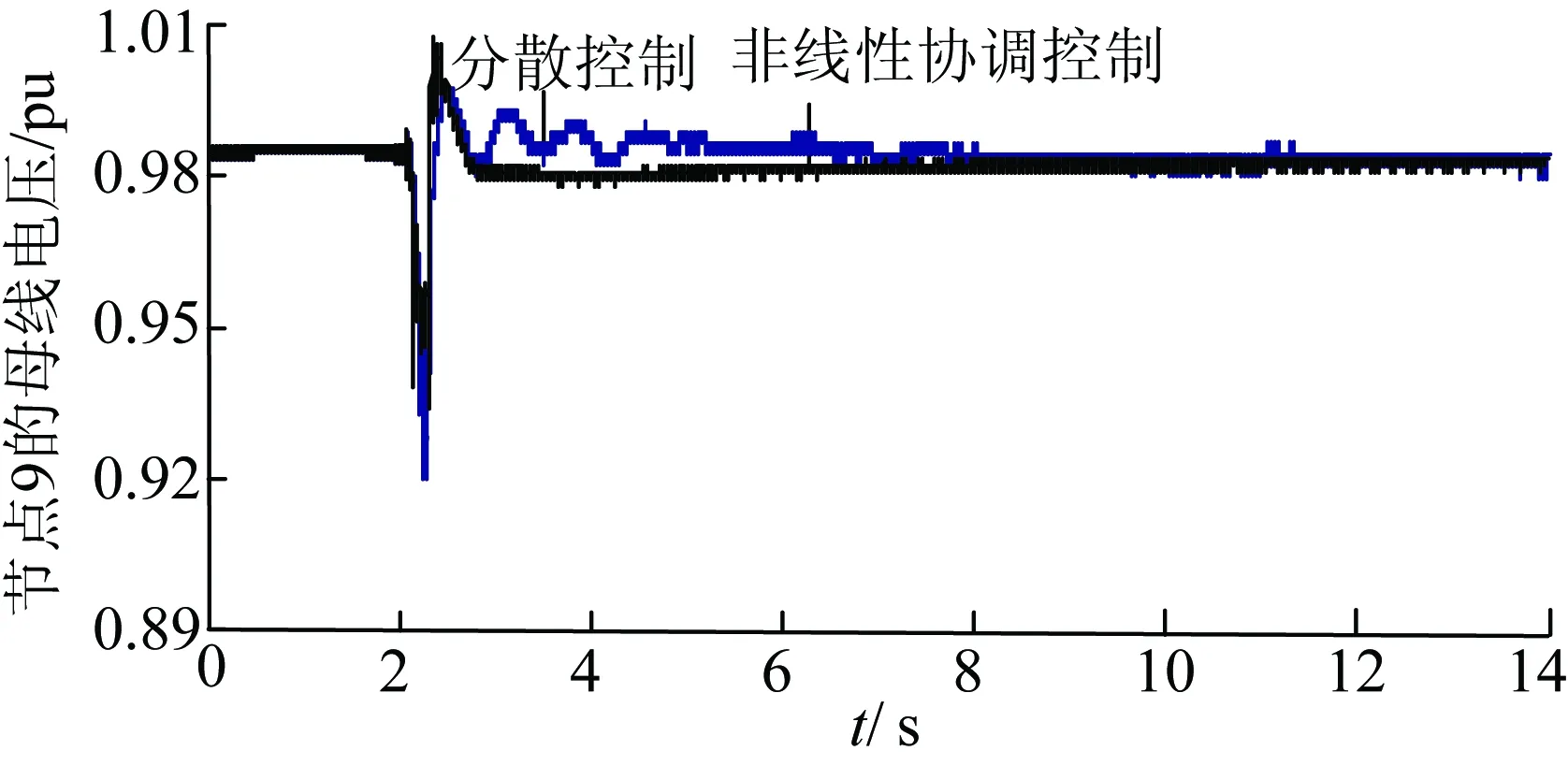
图8 母线9电压的响应曲线(故障2)
5 结 论
本文提出的多机电力系统中发电机励磁和SSSC的非线性协调控制策略具有以下优势和特点:(1)在协调控制策略的设计过程中充分利用了电力系统的内在结构特征,未进行任何线性化处理;(2)所提协调控制策略的表达式都比较简短,且其中所有控制变量都是可测变量,这使得协调控制策略有利于工程应用;(3)本文给出了利用广义Hamilton理论设计SSSC与发电机励磁协调控制的一般方法,这为研究多台发电机励磁与多台SSSC的协调控制提供了新途径。
[1]王旭,祁万春,黄俊辉,等.柔性交流输电技术在江苏电网中的应用[J].电力建设,2014,35(11):92-96. WANG Xu,QI Wanchun,HUANG Junhui,et al.Application of FACTS in Jiangsu power grid[J].Electric Power Construction,2014,35(11):92-96.
[2]邢士辉.柔性交流输电技术的现状及未来[J].电力建设,2005,26(8):21-23. XING Shihui.Current status and future of AC flexible transmission technology[J].Electric Power Construction,2005,26(8):21-23.
[3]李娟,周兴福,李淑琴.基于精确反馈线性化方法的SSSC非线性控制器[J].电网技术,2008,32(增刊2):12-15. LI Juan,ZHOU Xingfu,LI Shuqin.Nonlinear controller of SSSC based on exact feedback linearization[J].Power System Technology,2008,32(Supplement 2):12-15.
[4]周洋,江道灼,陈峰,等.基于模块化多电平换流器的限流式统一潮流控制器的设计[J].电力建设,2015,36(5):7-13. ZHOU Yang,JIANG Daozhuo,CHEN Feng,et al.Unified power flow controller design with fault current limiting based on modular multilevel converters[J].Electric Power Construction,2015,36(5):7-13.
[5]樊华,王丹,毛承雄,等.SSSC与发电机励磁最优协调控制[J].电力系统及其自动化学报,2015,27(1):13-18. FAN Hua,WANG Dan,MAO Chengxiong,et al.Optimal coordinated control of SSSC and generator excitation[J].Proceedings of the CSU-EPSA,2015,27(1):13-18.
[6]颜伟,吴文胜,华智明,等.SSSC非线性控制的直接反馈线性化方法[J]. 中国电机工程学报,2003,23(3):65-68. YAN Wei,WU Wensheng,HUA Zhiming,et al.Direct feedback linearization method for designing SSSC nonlinear control law[J].Proceedings of the CSEE,2003,23(3):65-68.
[7]胡益,王晓茹,李鹏,等.静止同步串联补偿器(SSSC)的非线性鲁棒H控制策略研究[J].电力系统保护与控制,2015,43(7):30-36. HU Yi,WANG Xiaoru,LI Peng,et al.Nonlinear robust strategy static synchronous series compensator(SSSC) of Hcontrol[J].Power System Protection and Control,2015,43(7):30-36.
[8]王玉振.广义Hamilton控制系统理论:实现、控制与应用[M].北京:科学出版社,2007:249-274.
[9]ORTEGA R,GALAZ M,ASTOLFI A,et al.Transient stabilization of multimachine power systems with nontrivial transfer conductances[J].IEEE Transactions on Automatic Control,2005,50(1):60-75.
[10]石访,王杰.伪广义哈密顿理论及其在多机电力系统非线性励磁控制中的应用[J].中国电机工程学报,2011,31(19):67-74. SHI Fang,WANG Jie.Pseudo-generalized Hamiltonian theory and its application to multi-machine power system nonlinear excitation control[J].Proceedings of the CSEE,2011,31(19):67-74.
[11]何斌,张秀彬.基于结构保持模型的多SVC协调控制[J].中国电机工程学报,2007,27(28):34-39. HE Bin,ZHANG Xiubin.Coordinated control for multi-SVCs based on structure preserving model of power system[J].Proceedings of the CSEE,2007,27(28):34-39.
[12]LIU Y,CHEN T,LI C,et al. Energy-based disturbance attenuation excitation control of differential algebraic power systems[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2008, 55(10): 1081-1085.
[13]SUN Y, SHEN T, ORTEGA R, et al. Decentralized controller design for multimachine power systems based on the Hamiltonian structure[C]//Proceedings of the 40th IEEE Conference on Decision and Control, 2001. Orlando, Florido: IEEE, 2001: 3045-3050.
[14]LIU Q J,SUN Y Z,SHEN T L,et al. Adaptive nonlinear co-ordinated excitation and STATCOM controller based on Hamiltonian structure for multimachine-power-system stability enhancement[J]. IEE Proceedings-Control Theory and Applications, 2003, 150(3): 285-294.
[15]DONG L,CROW M L,YANG Z,et al.A reconfigurable FACTS system for university laboratories[J].IEEE Transactions on Power Systems,2004,19(1):120-128.
[16]KUNDUR P. Power system stability and control[M]. New York: McGraw-Hill, 1994:813-815.
(编辑 景贺峰)
Nonlinear Robust Coordinated Control of Generator Excitation and SSSC for Multi-Machine Power Systems
LIU Qing, ZHANG Lina,CHEN Shichao
(School of Electrical & Electronic Engineering, North China Electric Power University, Baoding 071003, Hebei Province, China)
This paper discusses the coordinated control problem of generator excitation and static synchronous series compensator (SSSC) in multi-machine power systems and designs the nonlinear coordinated controller based on generalized Hamiltonian theory. SSSC adopts a third order model with considering internal dynamics and the interaction between SSSC and each generator is represented as additional electromagnetic power. The multi-machine power systems with generator excitation and SSSC is represented as a form of generalized dissipation Hamilton system. The coordinated control strategy of generator excitation and SSSC is designed by boundary-function method andL2disturbance attenuation method. The simulation results in two-area four-generator systems show that the proposed nonlinear coordinated controller can effectively improve the system transient stability and voltage regulation performance compared with the traditional decentralized controller.
generator excitation; static synchronous series compensator (SSSC); generalized Hamiltonian theory; nonlinear robust coordinated control
TM 762
A
1000-7229(2016)11-0129-06
10.3969/j.issn.1000-7229.2016.11.019
2016-07-12
刘青(1974),女,博士,副教授,主要研究方向为电力系统继电保护、电力系统安全防御与恢复控制;
张立娜(1989),女,硕士研究生,主要研究方向为柔性交流输电与智能电网;
陈世超(1991),男,硕士研究生,主要研究方向为电力电子技术应用及新能源发电。
