基于序优化方法的主动配电网调度优化决策
2017-01-10邵传军崔晓青于光远王志磊
邵传军,崔晓青,于光远,王志磊
(国网济南供电公司,济南市250012)
基于序优化方法的主动配电网调度优化决策
邵传军,崔晓青,于光远,王志磊
(国网济南供电公司,济南市250012)
近年来,随着可再生能源发电技术快速发展,电网中可再生能源的渗透率不断提高。主动配电网技术被认为是实现可再生能源高效消纳的一种有效解决方案。主动配电网的调度决策深刻影响着配电网的可靠性与经济性,是主动配电网实现其应用价值的核心技术,因此研究主动配电网的调度优化决策方法具有重要的现实意义。该文针对同时具有分布式光伏、风电以及储能设备的主动配电网,建立了考虑分布式电源特性与电价影响的主动配电网调度优化决策模型,并利用序优化方法进行快速高效求解,得到主动配电网在运行周期内的最优调度策略。最后,利用某实际配电网的算例验证了该文提出的主动配电网调度优化决策方法的有效性。
主动配电网;分布式电源;储能设备;电价;调度优化决策
0 引 言
近年来,随着分布式发电以及储能技术的快速发展,主动配电网技术逐渐受到人们的关注[1-2]。主动配电网是指使用灵活的网络拓扑来管理潮流,以便对局部的分布式能源进行主动控制和主动管理的配电系统[3]。主动配电网具有灵活的运行方式,被认为是实现高效消纳分布式电源和可再生能源的有效解决方案[4-5]。
主动配电网与被动配电网的不同之处在于主动配电网为有源配电系统,具备双向调度功能[6]。主动配电网内部普遍包含分布式电源。一些主动配电网内还有储能系统、电动汽车充电站等。主动配电网的调度优化决策深刻影响着配电网的可靠性与经济性,是主动配电网实现其应用价值的核心技术。研究主动配电网的调度优化决策方法具有重要的现实意义:一方面有利于提高配电网的安全性、可靠性、经济性;另一方面有利于促进分布式发电等相关智能电网技术的进一步发展。
在主动配电网调度优化决策相关研究中,具有一些有代表性的研究成果。文献[7]提出了以运行成本最低为目标函数的调度优化模型,并利用智能单粒子优化算法进行求解,但该模型中未考虑储能装置;文献[8]基于机会约束规划建立了含有风电、光伏和储能装置的能量调度随机数学模型,并使用改进粒子群算法进行求解,但未考虑电价影响与主动配电网网络拓扑情况;文献[9]以柔性负荷为研究对象,构建了综合考虑可再生能源利用率、网络损耗和用户满意度的主动配电网优化调度模型,但柔性负荷应用场景较少,具有一定局限性。
目前针对主动配电网调度优化决策的研究主要从提升经济性、平抑波动性和配合负荷特性等角度切入,但尚没有构建一个能够同时计及分布式电源、储能设备、电价影响以及主动配电网拓扑的调度优化决策模型。为此,本文针对同时具有分布式光伏、风电以及储能设备的主动配电网,建立考虑分布式发电特性与分时电价影响的主动配电网调度优化决策模型,并利用序优化方法进行快速高效求解,得到主动配电网在运行周期内的最优调度策略。
1 研究框架
本文整体研究思路如图1所示。首先,对主动配电网中的分布式电源的功率特性以及储能装置的运行特性进行分析,并建立相应的运行约束条件;其次,基于主动配电网的拓扑可变特性,建立主动配电网拓扑约束;然后,引入电价影响机制,对分时电价影响机制建模;最后,建立主动配电网调度优化决策模型,并通过序优化方法求解,得到主动配电网的调度策略。
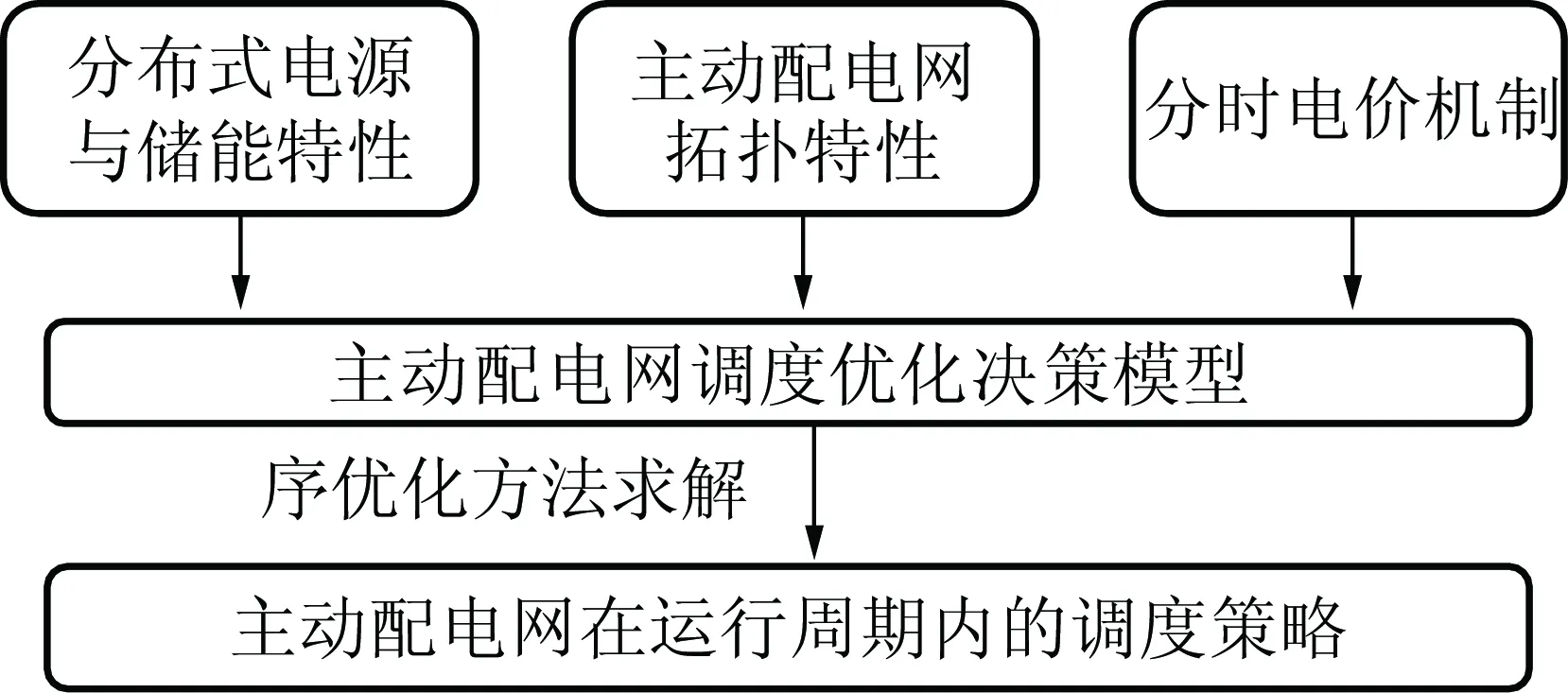
图1 整体研究思路示意图
2 数学建模
主动配电网的系统架构如图2所示。除了负荷之外,主动配电网内通常还包括分布式电源、储能装置等可调度设备,并具备调度决策系统充当主动配电网“大脑”的角色。调度决策系统根据输电网边界条件以及自身设备状态对可调度设备进行调度优化决策。

图2 典型主动配电网系统架构示意图
本文将以日前主动配电网调度优化决策为研究对象,基于分布式电源与储能装置特性、主动配电网拓扑特性以及分时电价影响机制,建立相应的优化决策数学模型,如下详述。
2.1 主动配电网拓扑特性
主动配电网具有网络拓扑可变的特性,可根据调度运行需求灵活开、合配电线路,提升配电网运行效率。
主动配电网在运行过程中,有3个基础要求:连通性,即保证所有负荷与供电系统相连;充裕性,即保证所有负荷均可被可靠供电;安全性,即所有输电线路均运行在输送容量限制范围内。在建模过程中为了满足主动配电网的基础要求,需要建立相应的约束。
2.1.1 连通性约束
为保证配电网呈辐射状连通,式(1)给出了主动配电网连通性约束:
I(t)∈T,∀t
(1)
式中:I(t)为t时刻的配电网的联络开关方案;T为配电网的连通辐射状结构的集合。
2.1.2 充裕性约束
为保证所有负荷均被可靠供电,建立针对每一节点的功率平衡约束:
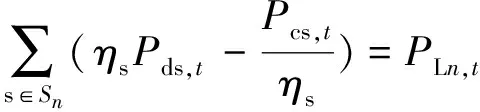
(2)
式中:Gn、Nn、Sn分别为位于节点n的机组集合、配电网内与节点n相连节点的集合、位于节点n的储能设备集合;ΩN为配电网的节点集合;Pg,t、Pg,t′分别为分布式电源g在t时刻的出力预测值、弃电功率,其中Pg,t′不能超过出力预测值Pg,t,如式(3)的所示;Pnr,t为节点n在t时刻通过线路nr向节点r传输的功率;Pds,t、Pcs,t分别为储能设备s在t时刻的放电、充电功率;ηs为储能设备s的充、放电效率;PLn,t为节点n在t时刻的负荷值。
0≤Pg,t′≤Pg,t,∀g,t
(3)
2.1.3 安全性约束
式(4)给出了线路输送功率的约束:
(4)
式中Snr为线路nr的最大输送容量。
线路输送功率的表达式如下:
Pnr,t=(δn,t-δr,t)/(Xnr+M-MInr,t)
(5)
式中:δn,t为节点n在t时刻的相角,rad;Xnr为线路nr的电抗标幺值, pu;Inr,t为线路nr上联络开关的状态,线路nr连通时,Inr,t=1,线路nr断开时,Inr,t=0;M为无限大的正数。
当线路nr断开时,式(5)分母趋于无穷大,线路输送功率为趋于0的无穷小值。
2.2 分布式电源与储能特性
2.2.1 分布式电源相关约束
由于分布式电源的出力具有高度的随机性与波动性,主动配电网调度决策需要提供一定的备用资源,以满足分布式电源对配电网灵活性的要求。配电网正、负备用资源约束分别如式(6)—(7)所示:
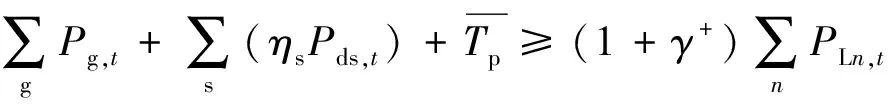
(6)
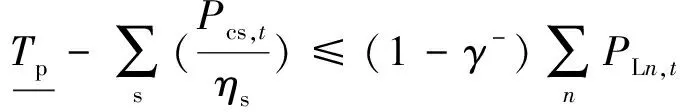
(7)

2.2.2 储能设备运行特性相关约束
(1)充、放电功率约束:
0≤Pcs, t≤Ics, t·Ps, max,∀s,t
(8)
0≤Pds, t≤Ids, t·Ps, max,∀s,t
(9)
式中:Ics,t、Ids,t为储能设备状态变量,当储能设备s在充电状态时,Ics,t=1,Ids,t=0,当储能设备s在放电状态时,Ics,t=0,Ids,t=1;Ps, max为储能设备s的充、放电功率最大值。
(2)充、放电状态约束:
Ics, t+Ids, t≤1, ∀s,t
(10)
(3)储能系统能量(state of charge,SOC)约束:
(11)
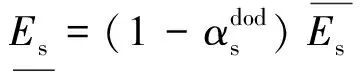
(12)
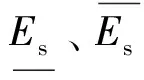
(4)储能系统能量约束:
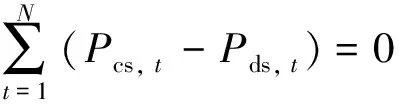
(13)
式中N为调度周期内的时段数。
本文假定每一调度周期内储能系统充电电量与放电电量相等。
2.3 电价机制
作为输、配电网间交互的边界条件,电价通过影响调度运行成本而影响目标函数,而深刻影响配电网的调度运行,因而电价机制的不同,也将影响主动配电网的调度优化结果。电价机制有恒定电价、两部制电价、阶梯电价、分时电价、实时电价等多种类型。电价大多从用电时间、用电量、负荷水平3个维度制定。
本文假设输、配电网联络线传输功率电价机制为分时电价。峰荷时段电价记为πp;谷荷时段电价记为πv;其他时段电价记为πg。分时电价机制下,配电网会通过优化调度策略来保证峰荷时段的稳定运行,并抑制峰荷时段电力负荷需求。
2.4 主动配电网运行决策目标
主动配电网的调度优化决策目标通常包括:(1)更高的负荷供电可靠性,以满足用户的用电需求为首要目标,通常情况下不允许切负荷;(2)更高的风电和光伏发电消纳率,最大限度地减少弃风量和弃光量;(3)更低的分布式电源与储能装置运行成本,提高经济效率;(4)更低的输电网侧用电电价或更高的上网电价;(5)更少去调用输电网侧的调节能力,即保证主动配电网自身充裕的灵活性,以应对分布式电源出力的不确定性。基于此决策目标,构建主动配电网调度优化决策目标函数:
(14)
(15)
(16)
(17)
(18)式中:Fcurt为弃电惩罚费用;γcurt为单位弃电惩罚费用;Funit为常规机组运行成本;fg,t为分布式电源g的单位发电成本;Fstor为储能装置运行成本,体现为能量转换的损耗;γstor为单位损耗成本;Felec为输电网侧联络线用电电费;πt为输、配电网联络线传输功率电价,在不同负荷时段对应不同的电价;PTm0,t为配电网与输电网联络线传输功率(假设配电网与输电网连接的节点号为0,外部节点为m,且δm,t=0)。
由于风电与光伏出力具有高度的不确定性,因此生成n个风电与光伏出力场景,式(14)中的目标函数为这n个场景的平均值。需要说明的是,在调度优化决策时,不允许切负荷。
2.5 序优化方法求解
以式(14)为目标函数、式(1)—(13)为约束条件的主动配电网调度优化决策模型属于混合整数非线性规划,计算负担较高。当配电网规模增长时,对计算能力提出较高要求。为了提高求解效率,本文采用序优化方法进行求解。该方法是由何毓琦[10]等学者于20世纪末提出的一种处理基于模拟仿真进行优化的重要方法,已成功使用到了许多实际应用当中[11-13]。该方法核心思想如图3所示,θN是共包含N个元素的总优化空间集合。利用特定选取规则,从中选出含S个元素的子集θS,θS中应至少有k个解属于由足够好的解组成的子集θG(θG有G个元素),且其概率Pr{θG∩θS的元素个数大于或等于k}需要大于给定概率目标。该方法定义了如图4所示的5种排序性能曲线,通过粗略模型评估θN中N个决策解,所有优化问题均可以根据这N个解的模型目标值排序结果来确定其所属的性能曲线类型。属于不同类型优化问题序优化求解时使用的参数不同。在本文中,采用去掉如式(1)所示约束条件后的粗略优化模型。在确定性能曲线类型之后,最优解的估计值可通过如下步骤得到:(1)给定θG的空间大小以及k值;(2)评估粗略模型的偏差;(3)确定θS的元素个数,即S值;(4)得到最优解的估计值。详细方法请见文献[10],在此不赘述。
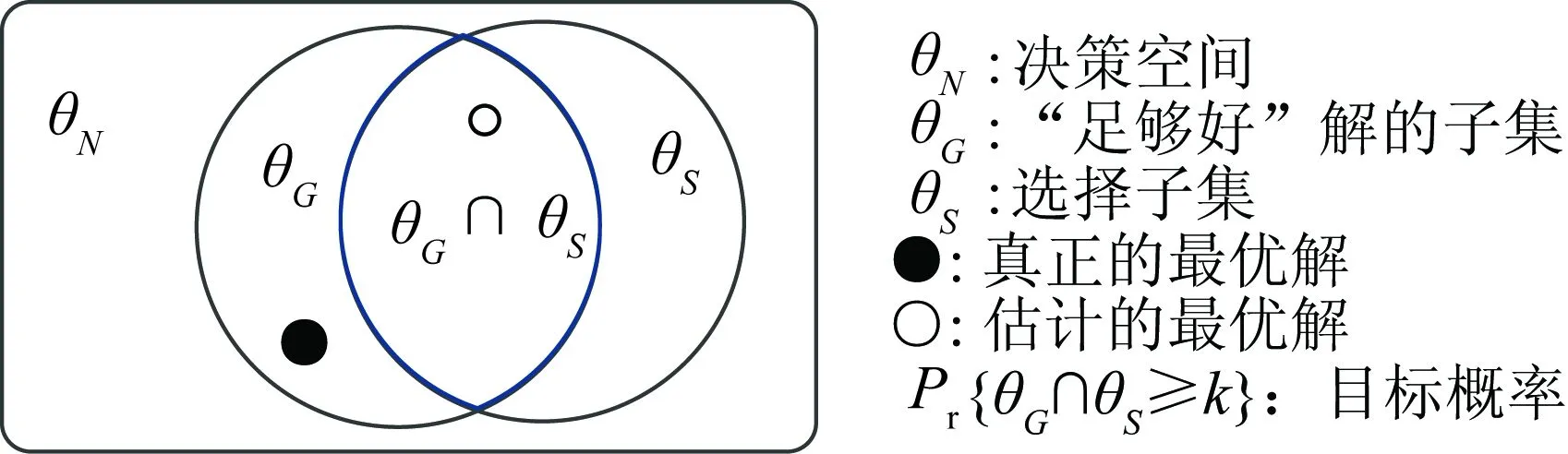
图3 序优化方法基本思想示意图
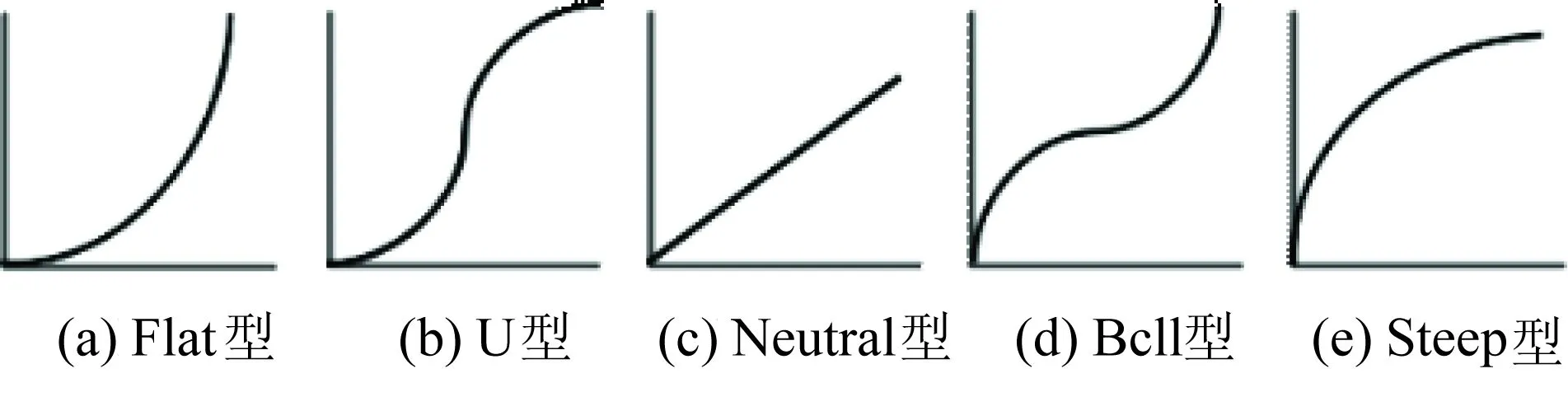
图4 排序性能曲线类型
3 算例分析
3.1 基本数据
以我国某省份的主动型配电网为例,其网络拓扑如图5所示。该配电网共有10个支路开关,其中C1~C7为关键负荷,采用双回路供电设计;有2个风电机组、3个光伏机组、4个储能设备,参数见表1。配电网总负荷如图6所示。风力发电与光伏发电出力预测值如图7所示。采用本文提出的基于序优化的调度策略对该算例1天24 h的配电网进行调度优化决策。为了不失一般性,假设所有支路线路参数一致。
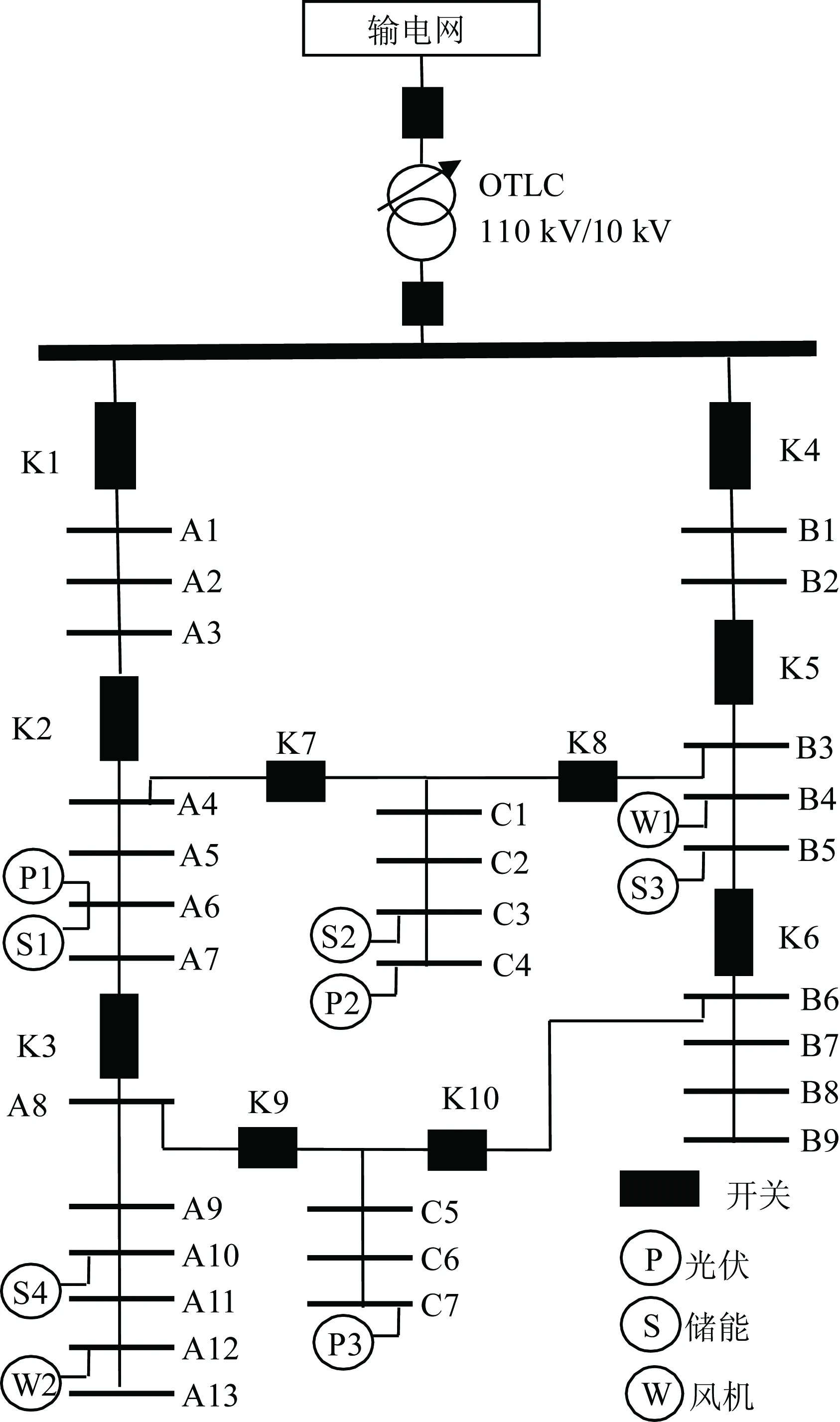
图5 主动配电网算例示意图
基于Python 2.7.11建立该算例的调度模型,计算平台为Macbook Pro (配置2.2 GHz Intel Core i7处理器和16 GB内存),总计算时间长度为3.6 s。
表1 模型基本参数
Table 1 Basic parameters of model
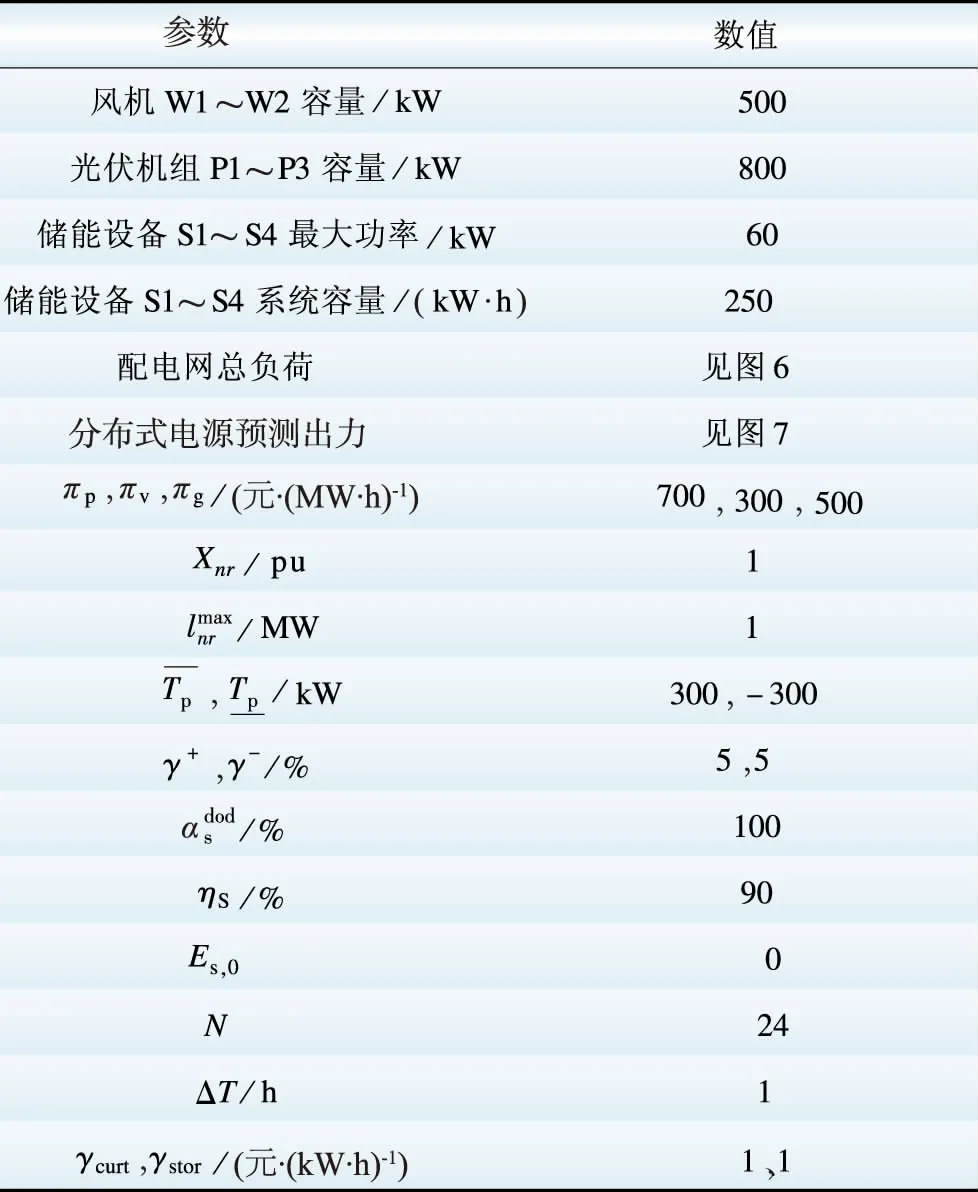

图6 配电网总负荷
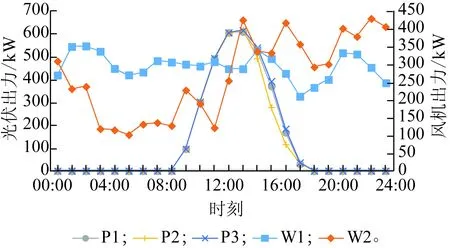
图7 风力发电与光伏发电出力预测值
3.2 结果分析
设定光伏与风电出力的预测误差服从正态分布,误差标准差为10%。生成2 000个风光出力场景,利用序优化方法求解,通过粗略数学模型评估得到的排序性能曲线如图8所示,为Bell型。

图8 排序性能曲线计算结果
设k=1。假设θG由解空间中前1%的优化解组成,则θG中足够好的解的数目g为2 000个×1%=20个。假设粗略模型与精细化模型的偏差服从均匀分布U(-w,w),需要对w进行评估。通过选择出50个粗略模型进行精细优化,可以得到w的统计结果,即w=0.21。因为50个样本相对较少,保守起见,我们将这一数字放大为2倍值,即w=0.42,此时w位于区间[-0.5, 0.5]之内,θS所含元素数目s可由式(19)确定:
s=‖θS‖=「eZσkρgγ+η⎤
(19)
式中:||·||为求集合的元素个数的符号;「·⎤为向上取整符号;根据文献[14],Zσ=8.199 8、ρ= 1.916 4、γ=-2.025 0、η=10.00。
由式(19)计算得s=19。因此,我们选择出 2 000个粗略评估过程中最优的19个解进行精细化评估,得到最优解。经程序计算,最优开关状态为K4与K10断开、其余开关接通,且无风电、光伏弃电,配电网运行成本(目标函数值)为2.94万元,较未采用优化调度优化时3.07万元的运行成本,降低了4.2%。
储能设备的充、放电决策结果如图9所示。当输电网电价处于低谷时,储能设备进行充电;当输电网电价处于高峰时,储能设备放电,以此来压低购用电成本。
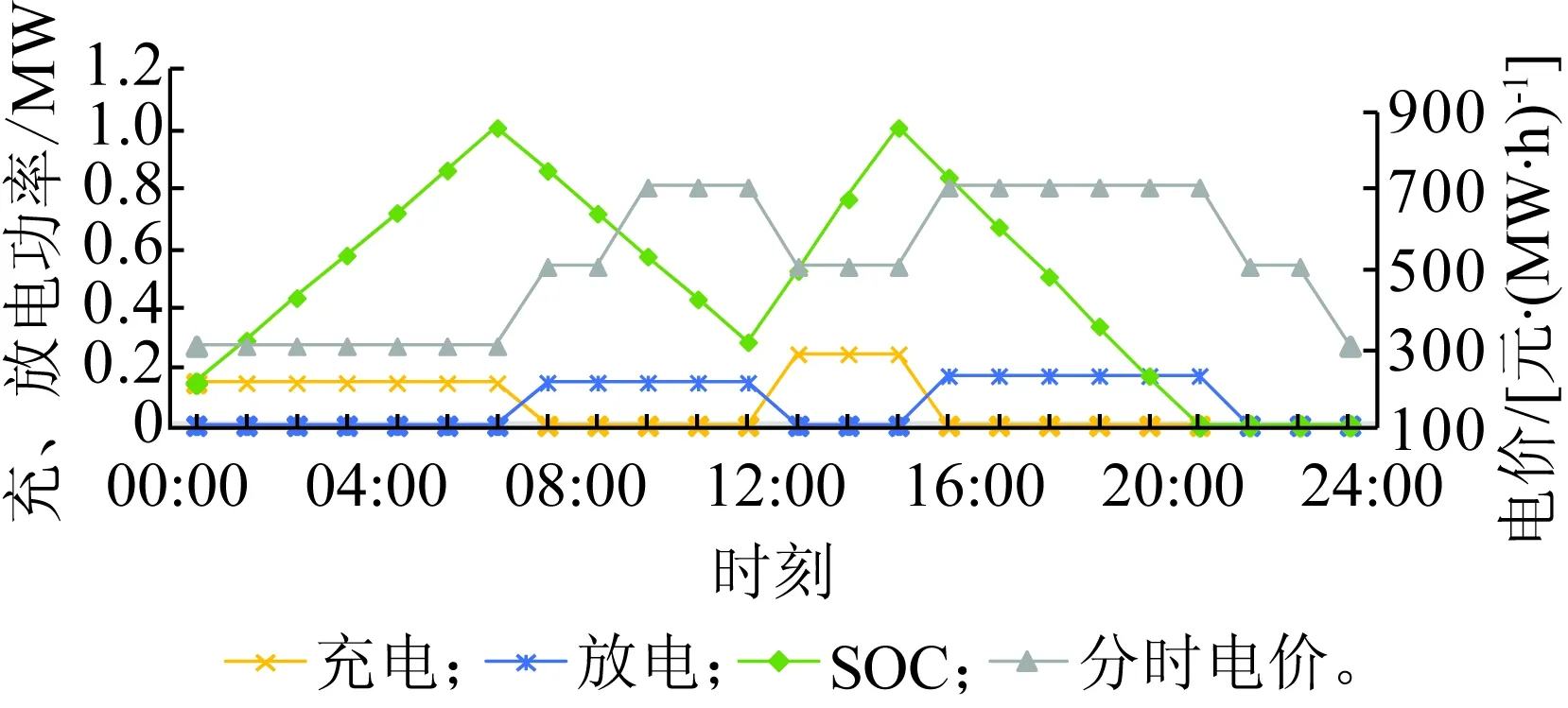
图9 主动配电网储能设备充、放电功率与分时电价情况
图10为分布式电源并网前、后的配电网负荷变化情况,以及考虑储能设备充、放电行为后的配电网最终净负荷。由图10可见,分布式电源并网后负荷曲线被压低。同时,储能设备起到进一步削峰填谷的作用。
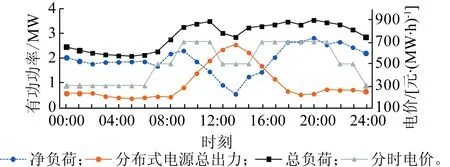
图10 配电网调度优化决策负荷情况
进一步,我们利用常规方法对模型进行了求解,因为模型高度复杂且非线性,首先忽略了连通性约束,其次将2 000个风光出力场景缩减为10个,最后利用CPLEX优化引擎求解,计算时间为17.9 s,运行成本为3.01万元,进一步证明了序优化方法求解的高效性。
4 结 论
本文提出了一种主动配电网调度优化决策模型,以分布式电源与储能特性、主动配电网拓扑特性、电价为基础,对主动配电网的调度运行进行数学建模,并利用序优化方法求解。算例结果表明,序优化方法求解效率较高,能够快速得到最优解的估计值,且所提出的方法能够降低主动配电网运行成本。在未来工作中,应进一步研究多个主动配电网系统协调优化调度与决策,使分布式电源与储能设备的利用效率得到进一步的提高。
[1]童亦斌, 吴学智, 唐芬, 等. 分布式光伏发电与主动配电网的协调发展[J]. 电力建设, 2015, 36(1):72-75. TONG Yibin, WU Xuezhi, TANG Fen, et al. Coordinated development of distributed photovoltaic generation and active distribution network[J]. Electric Power Construction, 2015, 36(1):72-75.
[2]丁明, 石雪梅. 新能源接入对主动配电网的影响[J]. 电力建设, 2015, 36(1):76-84. DING Ming, SHI Xuemei. Effect of new energy paralleling to the active distribution networks[J]. Electric Power Construction, 2015, 36(1):76-84.
[3]范明天,张祖平, 苏傲雪,等. 主动配电系统可行技术的研究[J]. 中国电机工程学报,2013, 33(22): 12-17. FAN Mingtian, ZHANG Zuping, SU Aoxue, et al. An investigation of enabling technologies for active distribution system[J]. Proceedings of the CSEE,2013, 33(22): 12-17.
[4]刘广一, 张凯, 舒彬. 主动配电网的6个主动与技术实现[J]. 电力建设, 2015, 36(1):33-37. LIU Guangyi, ZHANG Kai, SHU Bin. Six actives and key technologies of active distribution network[J]. Electric Power Construction, 2015, 36(1):33-37.
[5]程林, 刘琛, 康重庆, 等. 主动配电网关键技术分析与展望[J]. 电力建设, 2015, 36(1):26-32. CHENG Lin, LIU Chen, KANG Chongqing, et al. Analysis of development of key technologies in active distribution network [J]. Electric Power Construction, 2015, 36(1):26-32.
[6]金尧, 王正宇, 蒋传文,等. 主动配电网与主网协调调度[J]. 电力建设, 2016, 37(1):38-44. JIN Yao, WANG Zhengyu, JIANG Chuanwen, et al. Coordinative dispatching between active distribution network and main network[J].Electric Power Construction, 2016, 37(1):38-44.
[7]尤毅, 刘东, 钟清,等. 主动配电网优化调度策略研究[J]. 电力系统自动化, 2014, 38(9):177-183. YOU Yi, LIU Dong, ZHONG Qing, et al. Research on optimal schedule strategy for active distribution network[J]. Automation of Electric Power Systems, 2014, 38(9):177-183.
[8]王健, 谢桦, 孙健. 基于机会约束规划的主动配电网能量优化调度研究[J]. 电力系统保护与控制, 2014,42(13):45-52. WANG Jian, XIE Hua, SUN Jian. Study on energy dispatch strategy of active distribution network using chance-constrained programming[J]. Power System Protection and Control, 2014,42(13):45-52.
[9]沙熠, 邱晓燕, 宁雪姣,等. 协调储能与柔性负荷的主动配电网多目标优化调度[J]. 电网技术, 2016,40(5): 1394-1399. SHA Yi, QIU Xiaoyan, NING Xuejiao, et al. Multi-objective optimization of active distribution network by coordinating energy storage system and flexible load[J]. Power System Technology, 2016,40(5): 1394-1399.
[10]HO Y C,SREENIVAS R S,VAKILI P.Ordinal optimization of DEDS[J].Discrete Event Dynamic Systems,1992,2(1):61-88.
[11]LIN S Y,HO Y C,LIN C H.An ordinal optimization theory based algorithm for solving the optimal power flow problem with discrete control variables[J].IEEE Transactions on Power Systems,2004,19(1):276-286.
[12]GUAN X, HO Y C, LAI F.An ordinal optimization based bidding strategy for electric power suppliers in the daily energy market[J].IEEE Transactions on Power Systems,2001,16(4):788-797.
[13]XU Q, KANG C, XIA Q, et al.Anti-disaster transmission expansion planning considering wind power integration using ordinal optimization[C]//IEEE Power and Energy Society General Meeting. Nation Harbor, Maryland: IEEE,2014:1-5.
[14]LAU T W E,HO Y C. Universal alignment probabilities and subset selection for ordinal optimization[J]. Journal of Optimization Theory and Applications, 1997,93(3): 445-489.
(实习编辑 郭文瑞)
Dispatching Optimization Decision-Making of Active Distribution Network Based on Ordinal Optimization Theory
SHAO Chuanjun, CUI Xiaoqing, YU Guangyuan, WANG Zhilei
(State Grid Jinan Power Supply Company, Jinan 250012,China)
With the rapid development of renewable energy generation, the technique of active distribution network is taken as an effective solution to efficiently accommodate renewable energy in recent years. The dispatching strategy of active distribution network affects the reliability and economy of distribution network deeply, which is the key technique to realize the value of active distribution network. So it is of great value to conduct the research on the dispatching optimization decision-making of active distribution network. Focusing on the active distribution network with distributed photovoltaic, wind power and energy storage devices integrated, this paper proposes a dispatching optimization decision-making model considering the characteristics of distributed generation and electricity price. Based on the ordinal optimization theory, the optimal dispatching strategy of active distribution network for certain operation period can be achieved efficiently. Finally, a case study on a real distribution network is carried out to verify the effectiveness of the proposed dispatching optimization decision-making method for active distribution network.
active distribution network;distributed generation; energy storage devices; electricity price; dispatching strategy decision-making
TM 734
A
1000-7229(2016)11-0095-06
10.3969/j.issn.1000-7229.2016.11.014
2016-06-13
邵传军(1976),男,工程师,研究方向为电力系统规划、经济与可靠性;
崔晓青(1971),女,本科,高级经济师,研究方向为人力资源管理;
于光远(1985),男,硕士,工程师,研究方向为电网系统规划;
王志磊(1989),男,硕士,助理工程师,研究方向为电力系统规划与可靠性。
