储能优化配置关键问题分析

李丹丹，苏小林，阎晓霞，谭逸雪

(山西大学电力工程系，太原市 030013)

储能优化配置关键问题分析

李丹丹，苏小林，阎晓霞，谭逸雪

(山西大学电力工程系，太原市 030013)

储能优化配置是储能高效应用的基础，涉及技术和经济2个维度方面的问题，也涉及多应用时间尺度和功率能量的不同需求问题。基于储能在安全稳定、调频、新能源接纳、电能质量等方面的应用需求，深入分析了其优化配置的目标、条件、方法和理论。基于储能系统的成本效益分析，建立了通用净现值优化模型。结合不同储能的应用特性，分析了储能类型的选择原则，以及复合储能组合形式与容量配比的确定方法。针对储能应用的评价，从补偿效果、安全性、可靠性、经济性等方面给出了相关评价指标和评价方法。最后，提出了在储能应用实践中有待深入开展的研究性课题。

储能；电力系统；优化配置；评估指标

0 引 言

储能系统以其灵活的布局和智能充放能量的特性，打破了传统电能即发即用的限制，成为稳定电网运行，提高电力设备利用率，促进新能源并网，调整频率以及改善电能质量的重要手段。储能已成为现代电力系统的前沿技术和重要课题。目前关于储能的研究集中在4个方面：(1)高性能储能技术的研发，朝着快速、高效、低成本的方向发展；(2)优化配置，包括储能布局和容量规划；(3)协调控制，涉及不同储能之间的配合以及储能与电网现有控制设备和控制系统间的协调配合；(4)复合储能，利用多种储能的技术互补特性，同时满足电网不同应用环境下的多重需求，发挥其相对于单一储能的技术经济优势。

目前针对储能在电力系统中应用的综述主要侧重于各类型储能特性的介绍和对比、储能技术研发方向以及相关领域的工程应用现状等[1-3]，针对储能优化配置方面进行分析、评述的文献甚少。而储能优化配置是储能工程应用的首要问题，不仅为控制策略、优化运行奠定基础，同时恰当的选址定容对储能作用的充分发挥至关重要。结合不同应用需求开展储能的优化配置，充分挖掘储能应用带来的多种潜在价值，有效促进参与者的投资积极性，具有重大的理论意义和工程意义。本文从储能的应用需求、经济效益、应用类型以及应用评价等方面，深入分析储能规划过程中所需要解决的优化配置问题。

1 基于应用需求的储能配置

长期以来，很多学者致力于储能优化配置方面的研究，研究思路可以分为应用优先和经济优先两大类。储能应用在不同场合，对储能的应用时间尺度和功率能量要求均不同。根据系统的应用需求，选取适合的方法配置储能，以满足系统对安全稳定性、调频、新能源接纳和电能质量等方面的要求。

1.1 基于提高系统安全稳定性的储能配置

电力系统的动态稳定性一直是电力工作者的重点关注内容。随着新能源大量接入和电网互联不断发展，电网稳定运行主要受小干扰稳定、暂态稳定和电压稳定的威胁。围绕这几种稳定形式，国内外研究人员不断提出和应用新技术和新控制手段，例如电力系统稳定器(power system stabilizer,PSS)、高压直流(high voltage direct current，HVDC)辅助控制、柔性交流输电系统(flexible alternative current transmission systems,FACTS)附加控制、串并联无功补偿控制等。这些控制方式一般难以在同一个控制装置中实现有功和无功功率协调控制，无法兼顾满足功角、频率稳定和电压稳定的需求。储能作为一种新型稳定控制装置，通过控制电力电子换流装置，实现独立调节有功、无功功率的能力。

1.1.1 基于阻尼振荡和提高暂态稳定性的储能配置

PSS可以有效抑制电力系统局部振荡，但对于互联电网的复杂振荡模式控制效果并不理想，无法有效解决区域电网联络线间的功率振荡问题。而利用储能技术灵活的功率补偿特性可以抑制系统的低频振荡、次同步振荡以及扭振等。基于提高系统稳定性的储能配置，配置范围从简单局部网络延伸到多机复杂系统；优化方法初期多采用时域仿真法，逐步运用各种优化理论深入研究该类问题。

时域仿真法能够模拟电网受到扰动后系统的各个参量随时间变化的具体过渡过程,从而反映系统的稳定程度。通常从经验总结的角度出发，将储能单元连接在发电机出口母线处，以发电机转子角速度偏差Δω或输出有功功率变化ΔP作为控制信号进行建模仿真，直接对比分析系统功率振荡曲线、功角变化曲线，判断储能装置的控制效果，选择使系统最先恢复稳定的位置作为储能的最佳安装地点。选定安装位置后确定储能的容量，依次安装不同容量的储能，分别进行仿真实验，直到增加的储能容量不再使系统性能继续改善，设定此容量为该工况下所需最小储能容量。大量的研究分析和仿真结果表明，把储能装设在最先失稳的发电机机端,能最有效地提高系统的暂态稳定性。对于区域互联系统，在相同控制和运行条件下储能安装在功率接收端要好于安装在功率发出端，安装在两区域联络线中间对抑制区域间低频振荡效果最差[4]。时域仿真法可以直观地得到储能最佳安装地点以及容量的选择结果，但储能的控制效果是通过研究者观察曲线主观意识判断得出的，当仿真曲线较为接近时，则不易准确判断补偿效果的优劣，从而影响储能选址定容的精确性。因此，现多采用时域仿真法作为检验其他优化方法的手段。

另一种配置思路运用优化理论，提出合理、明确的量化标准指导储能选址定容。目前采用的配置方法主要有3类：(1)模态分析法，以系统线性状态方程为基础，分析特征值/特征向量，利用控制系数[5]以及典型参数的灵敏度分析等方法指导储能配置；(2)暂态能量函数法，分析系统受大扰动后分布式储能布局问题；(3)智能优化算法，根据系统稳定控制目标建立目标函数，采用智能算法如遗传算法、免疫算法、禁忌搜索算法解决储能布局问题。文献[6]依据留数指标和参与因子指导飞轮储能布局，结果表明该方法可以有效抑制系统低频振荡；文献[7-8]建立暂态性能评价指标，根据超导磁储能(superconducting magnetic energy storage， SMES)在故障条件下改善发电机响应的程度，分别采用禁忌搜索算法和遗传算法对储能选址进行优化。对于提高暂态稳定性的储能布局问题，无论首先进行系统故障扫描[9]或预测预想事故集[10]或找出电网敏感支路，其目的都是要确定系统薄弱环节，作为储能布局的初步筛选点。再进一步结合优化理论，准确定位储能的接入位置和选择配置容量。文献[9]确定薄弱环节后，以系统的暂态能量分布情况作为储能布局依据，定点后以稳定状态偏离值最小为指标计算最优容量。文献[10]考虑系统不确定因素和事故发生的概率和后果，基于暂态稳定风险理论指导储能优化配置。每种配置方法均对应一定的适用范围，例如针对抑制系统振荡的SMES选址，最大特征值法对于SMES容量很大的情况有效[11]。但如果SMES的容量较小时，由于此时SMES影响特征向量值的能力很弱，因而无法通过特征值准确判断最佳位置。所以针对电网规模和稳定类型选择合适的优化理论和方法对于储能的合理配置至关重要。

关于提高电力系统动态稳定性的定容问题，目前主要有2个方面障碍：一是如何将稳定性的定性问题转化成定量指标进行研究；二是储能容量在动态电力系统中的量化问题。

1.1.2 基于提高电压稳定性的储能配置

风能是一种间歇性能源，且风速预测存在一定误差，导致风电场不能提供持续稳定的电能。大量分布式电源分散接入配电网，给电网运行与控制带来新的机遇和挑战。当风电场出力较高时，风电场的无功需求以及输电线路的无功损耗增加，造成局部电网无功不足，电压稳定裕度下降，危及电网的安全稳定运行。目前风电场多采用静止无功补偿器(static var compensator，SVC)快速补偿无功功率，维持并网点电压稳定，但SVC不能控制风电场输出的有功功率。储能可满足协调控制电网有功、无功功率的需求，能有效改善并网风电场的稳定性。

电网的电压稳定极限限制了风电场最大装机容量。目前研究热点集中在最大风电接纳能力下的电网电压稳定性，主要依据改善电压分布、增大电压稳定裕度计算需要配置的最小储能容量。通常以区域电网P-U曲线为切入点，从稳定运行开始，通过不断加大风电场出力绘制电压变化曲线，直到达到电压稳定临界值，该时刻对应的风电容量为风电场最大接纳水平，而实际风电场容量与最大值之差则为储能需求量。此种定容方法依赖于风电场出力数据的典型性，并没有为考虑其他运行因素留有一定裕度，不利于风电场的扩容建设。在此基础上，可以依据电压裕度[12]、传输线路输电裕度的需求，细化所需接入的最小储能容量。

1.1.3 基于提高安全性的储能配置

基于提高系统安全性的储能容量配置，关键在于如何将安全稳定的定性问题转化成定量指标进行研究，常从电压安全裕度和切负荷量2个角度评估电网安全性。文献[13]提出基于潮流跟踪的储能选址方法，根据负载率均衡度和电网最小切负荷损失这2个指标配置储能最优容量，提高电网静态安全性。

关于提高电力系统安全稳定性的配置问题，大多是基于特定的运行工况得到优化结果，而实际电网的运行方式和故障情况复杂多变，所得结论能否满足不同工作状态下系统的安全稳定，需要适合实际工程应用的储能优化配置方法。

1.2 基于参与电网调频的储能配置

在新能源大量接入以及传统机组调频容量有限的情况下，利用储能电源反应快速的特点调节系统频率，既可以避免发电机组的过度磨损，又可以部分补充系统备用容量，从而达到提升电能品质的目的[14]。储能参与系统调频的运行方式主要有3种：(1)与新能源发电结合参与调频；(2)辅助火电机组调频；(3)储能独立运行调频。国内外针对储能参与电网调频的研究主要聚焦在前2种运行模式上。当需要储能辅助一次调频机组动作时，应尽量将储能装置安装在需要配合的机组母线侧，以便接受相同变化指令调整出力。接受指令后可以对比所选储能类型的动作时间和一次调频机组的动作快慢，合理安排调频动作顺序。对于储能配合自动发电控制(automatic generation control，AGC)机组的频率调整,按比例分配一定负荷给储能装置，由此补充备用容量的不足。

参与调频对储能的响应速度和功率容量都有一定要求，所以一般选择锂电池、液流电池辅助系统调频。电池容量配置一般分别针对一次调频或者二次调频。配置原理基于模拟区域电网的常规机组的下垂特性和基于调节负荷分量曲线，可以根据电池容量和荷电状态(state of charge,SOC)上下限值[15-16]解决电池参与调频的动作时机和动作深度问题。配置方案通常以系统运行效益最大为目标，在此基础上可以考虑不同调频补偿方式对调频盈利结果的影响[17]。文献[18]通过分析灵敏度系数的特征，合理安排动作时机，同时结合调频评估指标要求确定动作深度，并根据所必需的动作深度与额定功率之间的关系形成储能容量配置方法。文献[16]在动态调整SOC的基础上，基于经济性考虑，采用增加紧急电阻的新型控制算法，紧急电阻用在很少发生极端过频率的情景，当频率越限而电池容量满充时，利用其来消耗电能，减少配置电池的容量。

关于储能参与电网调频的容量配置研究尚处于探索阶段，目前也多针对一次调频规划储能容量。为提高储能的综合利用率，可以考虑同时满足一、二次调频需求，合理规划储能容量。

1.3 基于提高新能源接纳能力的储能配置

新能源发电并网形式多样，有输电侧大规模清洁能源并网、配网侧分布式发电接入以及微电网等，利用储能提高电网对新能源接入的友好性，是实现清洁能源大规模开发利用的重要途径之一。新能源接纳能力是在保证电网安全、稳定、经济运行的前提下，风电/光伏的极限注入功率，主要受该地区网架结构、运行水平、负荷特性以及风、光出力等多方面因素影响。目前多数研究忽略输电线路输送容量约束，而输电容量是导致弃风、弃光的关键因素。储能的配置方式分为分布式储能和集中式储能。对于风电场处的储能布局，储能可以分散安装在每一台风机内部或是集中配置在风电场并网点处。由于风电场多台风机的自平滑特性可以降低风电场输出总功率波动，因而采用一个独立的储能系统统一控制和调节整个风电场并网功率可以达到更好的平抑效果和最佳经济性。所以储能规划研究一般忽略风电场的多点分布，默认安装在风电场变电站低压侧，只对其容量配置进行探究。

新能源-储能联合发电的调控模式主要有：(1)平滑出力波动；(2)削峰填谷；(3)跟踪计划出力。配置储能实现功率调控以提高新能源接纳能力的研究主要为了满足上述技术目标的一种或多种[19-21]。文献[19]以能量型储能为研究对象，考虑跟踪计划出力和削峰填谷风储联合控制模式，讨论各敏感因素变化对储能最佳容量配置的影响。根据调控模式需求配置储能容量的研究中以改善风电场输出功率特性研究居多。

基于平滑出力波动，配置储能的功率/容量流程如图1所示。我国限制风电功率波动依据2个时间尺度：1 min和10 min，不同时间尺度提出明确的波动限制指标。根据限制指标进而选择适用于平滑风电功率波动的储能类型，需考虑储能响应时间和出力幅值2个参数，由此确定储能类型。根据不同的优化目标，风电并网输出参照的目标曲线也不同，如按照风电期望的平滑曲线输出或按照风电的功率预测曲线输出，最终需要储能补偿的容量差别较大。以目标曲线为依据，制定平滑控制策略，最常用的控制算法有低通滤波控制、滑动平均法、滚动平均法。得到最小或最优储能容量后，需对该方案进行可行性评估。

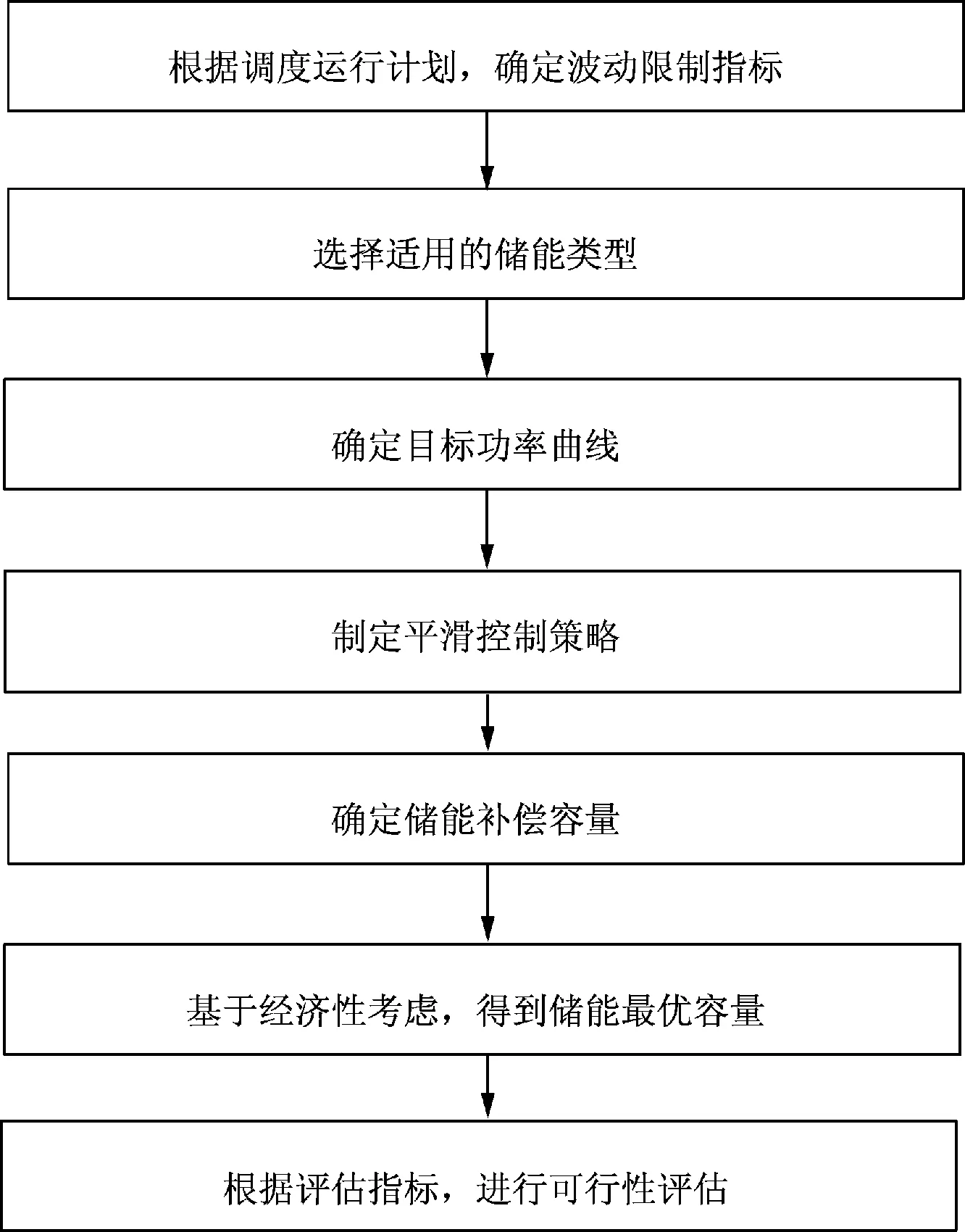
图1 基于平滑出力波动的储能配置流程Fig.1 Flow chart of ESS capacity allocation in wind farm for fluctuation mitigation

一阶低通滤波控制的原理是利用储能系统补偿风电功率在截止频率以上的高频分量，而在截止频率以下的功率可顺利通过低通滤波器，风电原始功率与滤波器输出值之差即为储能系统需要吸收/释放的功率，此方法的关键在于滤波时间常数的确定。平滑时间常数越大，平滑效果越好，但所需的储能功率和容量随之增大。因此需要从技术和成本的角度考虑选择合适的时间常数。文献[22]在研究平滑时间常数-电池容量特性的基础上，通过分析平滑时间常数-合成输出标准偏差这2种特性之间的关系，同时依据成本/性能比来确定合适的时间常数，使其既能满足风电输出平滑化的需求，又能使电池容量比较小。低通滤波法的缺点在于没有考虑储能自身参数，并且在某些功率变化较大的时刻点，输出功率会被大幅修正，因而对储能系统的功率能力提出较高要求。

滑动平均法是一种选择固定时间长度窗口，将窗口内的所有数值做算术平均，将平均值作为窗口中心点的数学方法。基于实际风电场风电功率预测曲线和风速概率密度曲线，计算得到的输出功率期望值设定为平均功率水平。然后人为对原始功率曲线划分时段，比较各个时段内实际功率与平均功率得到该时段需要配置的容量，最后取最大值设置为该风电场所需的储能功率和容量[23-24]。输出曲线划分的时间段越多，所需储能容量越小，但频繁充放电会影响储能寿命，而且区间段设置过小，风电功率预测的相对误差就越大，影响此方法的精确性，所以滑动平均法关键在于滑动时间窗口宽度的设定。滚动平均法原理与滑动平均法基本相同，但从配置结果上看，采用滑动平均法容量配置结果偏大[25]。

1.4 基于改善电能质量的储能配置

在配电网中低压侧合理装设储能系统，一方面提高电网对新能源的消纳能力，促进分布式发电的应用；另一方面可以改善供电负荷的电能质量。与电网侧相连的功率变换系统(power conrersion system, PCS)实时检测网侧电压，一旦检测出现电压波动、电压偏差超过允许限值或是发生电压中断等电能质量问题时，PCS控制储能系统输出维持敏感负荷所需要的能量，保证维持重要负荷正常工作的能力。储能改善电能质量属于功率型应用，所需的储能容量并不大，所以其一般配合其他优化目标进行容量规划。文献[26]建立了多目标最优潮流模型，实现有功损耗最小、无功补偿费用最低以及电压偏差最小的多重配置目标，以提高风电接纳能力。基于改善电能质量的储能配置，首先需要对波动分量进行分解，分析各部分波动量对电网电能质量的影响程度，从而配置一定容量的储能，补偿对电压、频率影响较大的分量。有学者采用傅里叶变换和希尔伯特-黄变换(Hilbert-Huang transform, HHT)分解不平衡量，分析得出HHT更适用于局部细节分析，在以提高电能质量为目标的储能配置方面具有独到优势[27]。

2 储能配置的经济性分析

储能在电力系统中各个场合应用的技术优势已经得到论证，但当前储能的单位成本昂贵导致储能接入系统后盈利区间有限。因此需全面分析储能的成本和效益，探究储能在电力系统中应用的必要性与可行性。

2.1 成本分析

考虑新能源与储能联合应用的成本主要来源于2个方面，一是储能装置投资成本；二是运行成本。风电场、光伏电站侧储能容量优化的目标是在满足波动率要求的前提下，以最低的储能投资成本和运行成本实现储能系统的运行效益最优。

2.1.1 投资成本

储能的投资成本主要包括[28]：站址建设成本、电能转换设备(包括交流侧变压器和断路器、整流/逆变系统)成本、储能系统(主要为蓄电池组和电池组管理系统)成本。前2种基本为固定成本，所以投资成本在于对储能自身成本的把控。多数研究粗略估计储能投资成本和运行维护费用，未能计及储能整个寿命周期内更换、失效保护所产生的费用[29]，此类费用对于充放电循环次数有限的电池类储能不容忽视。在实际运行过程中储能充/放电策略和运行环境会直接影响电池放电深度，而放电深度与蓄电池寿命密切相关，雨流计数法可以计算计及充放电深度的储能系统使用寿命[30]。

2.1.2 运行成本

以风电场为例说明运行成本，主要包含储能系统损失能量成本和风电场弃风成本2个部分[20]，两者均因储能容量的变化而变化。

储能系统损失能量由2种原因导致。一种是由电池容量限制产生的，即当电池电量处于满充状态后，蓄电池停止充电，多余的能量不能转换成电能储存；另一种是由电池的最大充电功率限制产生的，即当风电场实际输出功率与期望输出功率的差值大于电池的最大充电功率时，储能只能按照规定的最大充电功率充电，而无法以功率差值充电，此部分能量看做储能损失的能量。同样，风电场弃风能量也主要由这2种因素产生。另外还与系统的运行方式、调峰能力以及输电线路输送能力等因素相关联。文献[31]研究了风电场弃风成本、储能损失成本以及储能投资成本这3种成本间的制约关系，构建了储能容量经济优化计算模型。

储能投资成本与运行成本之间存在对立关系。由上述分析可知，储能容量越大，储能系统损失能量和风电场弃风能量越小，即运行成本降低。当前市场储能投资成本较高，风储系统运行过程中接纳适量的弃风能量，可以使风电场整体效益最优。如果盲目追求弃风能量最小，会大大增加储能容量而产生高昂的系统总成本，经济效益不佳。所以可以采用满足一定置信水平或基于机会约束规划的思想配置储能容量[32-33]，得到技术和经济性方面的权衡方案。

2.2 效益分析

储能的应用价值体现在多方面，一般研究只关注投资主体的直接经济利益，而忽略了对储能给电网和社会所带来的隐性经济价值的评估。如何量化储能效益，全面评估储能应用的综合效益，是推动储能大规模商业化发展的关键。

全方位衡量储能对系统的综合价值，应该涉及经济效益和社会效益2个方面。当前投资主体呈现多元化(包括发电公司、电网运营商、用户侧)，在效益评估时应明确各受益方利益，否则在考虑多种收益时，容易导致受益主体利益相矛盾。

2.2.1 经济效益

储能产生的经济效益是多方面的，储能系统应用于新能源发电中，可以获得低储高发套利带来的直接收益，还可以获得削峰填谷、减少系统旋转备用等间接收益；应用于发输电系统侧，能够通过延缓电网升级改造、减少输电阻塞、提供调频辅助服务等获利；应用于配电网侧和微网中能够通过降低缺电成本、减少有功网损等获得经济效益。不同研究偏重于不同方面进行规划，所以建立的模型各异。

2.2.2 社会效益

储能与新能源联合运行，快速推进清洁能源并网发电，减少化石燃料的消耗和废气排放，降低燃煤、燃气式发电在电源结构中的比例，在此过程中可以体现出储能带来的能源节约效益、环保效益、容量替代效益等，促进能源节约型、环境友好型社会的发展。文献[34]研究了基于需求侧响应的分布式光伏和储能容量配置，考虑负荷预测误差和负荷曲线波动的影响，目标兼顾成本费用最低和CO2排放量最小，最终结论为当光伏和储能系统的容量分别为峰值负荷的10%～15%、2%～3%时目标最优。

储能规划模型针对优化各类技术目标，结合成本和效益建立数学模型，且一般认为成本和效益是对于整个储能联合运行系统而言的，并不只是针对储能装置本身。以收益最大为目标函数的净现值优化模型如式(1)所示。约束条件需满足各种物理、运行、系统等因素制约。

(1)

式中：E为储能系统最优配置容量；RI为第t年的收益；CO为折算至第t年的成本；r为基准收益率；T为项目寿命；Rj(j=1，2，3，…)表示研究时段内储能通过低储高发套利、提供辅助服务、减少停电损失等所带来的相应收益；CBESS、Cr分别是电池全寿命周期内电池安装和运维费用、从电网购买电量的费用。

3 不同类型储能的配置分析

3.1 储能类型选择

压缩空气储能和抽水蓄能电站储能容量大，多用在配网侧提供能量管理和调频服务，小型电站可作为微网的能量缓冲环节。电磁类和电池类储能占地面积小，安装灵活，可满足输电网、配电网以及微网多种场合的应用需求。储能应用类型分为单一储能和复合储能两大类，单一储能有能量型和功率型元件之分。对储能容量需求不大但要求快速响应不平衡功率的场合选取功率型储能，相反在能量管理场合选择能量型储能。若针对某些应用对长短时间尺度都有要求的场合，则需要采用2种不同特性的储能类型构成复合储能系统。关于复合储能统的组成形式，常见的有各类先进电池配合超级电容器使用，还有介质特性差异较大的2种电池类组合(如全钒液流电池与铅酸电池联合使用)[35]。

3.2 复合储能

对于复合储能功率/容量的配置，一般思路为在储能组合类型确定后，基于储能成本分析，对不同储能装置进行协调控制，确定功率分配方案。得到储能功率配置结果后，继而结合运行时间计算得到容量值。整个配置流程关键在于如何将波动分量在各个储能元件中进行功率分配。

复合储能系统的功率分配常常通过高通滤波器方法实现。补偿方式为分频补偿，即功率型补偿高频分量，能量型补偿低频分量，所以功率分配重点是确定分界频率，即确定滤波时间常数。时间常数越大，功率型器件补偿功率越大，则能量型器件补偿功率越小。因此，实际应用中应结合具体场合的配置目标，采用遗传算法[30]、黄金分割法结合抛物线逼近法[36]确定分界频率，求解最优时间常数大小。除了高通滤波法，还可以利用小波分析法[37-38]、多孔算法[35]等优化方法分配复合储能的功率。文献[37]通过小波分析法解耦电池、超级电容器信号后，通过概率统计方法，分析了2种储能信号的分布特性，得出不同置信水平下的功率组合方案。以均值、方差、波动范围及波动点数为指标，比较各种方案平抑风电功率的效果。

围绕复合储能配置，除了合理的配置方法外，储能系统数学模型的精确性、复合储能元件的连接方式以及协调运行策略[39]对储能容量的优化配置至关重要。因此，有关复合储能的协调控制策略、经济规划和优化调度有待进一步研究。

4 储能配置效果评价分析

依据量化指标对储能作用效果进行评价，是体现储能应用价值的最直接手段，也是刺激投资主体积极性的重要方式。从波动补偿效果、系统安全性、供电可靠性、可再生能源浪费率和经济性方面，分别给定通用评价指标和评价依据。

4.1 补偿效果

波动变化率为相邻时间输出功率差的绝对值，常用作表征短时间尺度风电、光伏等输出波动大小的指标。标准偏差衡量一个随机变量偏离算数平均值的程度。一般用标准偏差作为评估长时间段内风电、光伏等输出波动的评估指标，计算表达式如式(2)所示：

(2)

式中：N为评估期内的离散点数；Pave为可再生能源平均输出功率。标准偏差越小，表征随机变量偏离均值越小，则说明输出曲线越平滑，补偿效果越好。

4.2 提高安全稳定裕度

安全稳定裕度反映了系统期望的安全运行风险水平，根据实际情况选择期望的系统运行风险水平，以灵活调整储能装置的配置方案。目前通用的的评价指标有最小切负荷量、负载率均衡度、暂态稳定裕度、电压越限距离、节点电压分布等。储能能够为电网提供暂态支撑能力，可以提高系统的故障极限切除时间(critical clearing time,CCT )。CCT是系统重要的运行参数，能够为安全经济调度和预防控制提供有价值的信息。当系统遭受故障时，CCT越小，说明在此种故障情况下系统稳定性越差，故可以采用极限切除时间作为评判储能增强系统稳定效果的指标。

节点电压是反映系统稳定性和电能质量的重要参数之一，电压偏移、电压波动值均可衡量储能改善供电电压质量的程度。电压分布指标量化储能作用后对电压稳定的改善效果，其计算如式(3)、(4)所示[40]：

(3)

(4)

式中：Ui表示节点电压幅值；Un表示额定电压；Umax、Umin分别表示节点电压最大、最小限值；N表示馈线节点数；Pj、Pi分别表示储能加入前后节点注入功率。

Upi反映节点电压质量，Upi越小，表示此节点电压偏离额定值距离越大，则说明加入储能对馈线电压分布影响越小。所以Upi的值越大越好。Up反映馈线综合电压分布质量，其值越大越好，上限值达到1时表示各个节点电压为标称电压。

4.3 供电可靠性

电网的任何功能都要从用户需求出发，从用户角度看，最为关心的是能否连续获得符合电能质量要求的电能，即系统能否提供良好的供电可靠性。一般选用负荷缺电率、供电损失率ηLPSP、供求匹配系数、平均系统停电时间TASIDI[41]等指标衡量储能配合其他形式电源构成联合发电系统的供电可靠性。

TASID选自最具代表性的IEEE配电可靠性指标标准，该指标定义如式(5)所示：

(5)

式中：ri为每次停电事件的恢复供电时间；Li表示每次停电事件所连的停电负荷， kV·A；Lr表示供电所连总负荷， kV·A。该指标提供系统平均停电持续时间，时间越短，说明系统供求平衡度越好，负荷失电量越少，供电可靠性越高。

4.4 可再生能源浪费率

很多文献采用能量浪费率ηEXC或能量损失率指标指导储能容量与可再生能源发电量的配比关系，间接反映增设储能装置对新能源利用率的影响。ηEXC为风光等发电浪费的功率与评估期负载要求的总功率的比值。当风光储总发电功率高于当前负荷所需要的功率时风力和光伏发电浪费的能量如式(6)所示[42]：

EW(t)=[PPV(t)+PWG(t)]Δt-

{Pref(t)Δt/ηinv+[Cbatmax-Cbat(t-1)]/ηcha}

(6)

式中：EW(t)是在满足负荷要求和储能元件最大充电容量要求的基础上，风力发电和光伏发电等浪费的能量；PPV(t)、PWG(t)为t时刻光伏发电、风力发电输出的有功功率；Δt为用于计算的步长；Pref(t)为负荷所需功率的参考值；ηinv为功率变换器效率；Cbatmax、Cbat(t-1)分别为储能系统的最大容量和t-1时刻的初始容量；ηcha为储能系统充电效率。

评估期T内，能量浪费率为

(7)

式中Pload(t)为评估期T内负载总功率。应尽量减小能量浪费率，以提高可再生能源利用率。

4.5 经济性

储能装置造价昂贵，其成本在整个联合发电系统的投资成本中占比很大，所以客观评估储能的经济价值是储能技术商业化推广应用的关键。目前采用的评价标准有针对储能使用寿命的评估指标(电池充放电次数、储能功率概率密度分布特性、SOC越限次数)和反映总体盈利能力的指标(净现值指标、投资回收期)。净现值越大，配置方案越优，投资效益越好。若净现值出现负值，则说明该方案在经济性上不可行，需调整储能配置方案。

投资回收期是工程项目的累计经济效益全部抵偿初始投资费用所需的时间，是反映项目财务投资回收能力的重要指标，计算公式如式(8)所示[43]:

(8)

式中：P0为初始投资；Rt为每年的净收益；Pt为投资回收期。回收期愈短，资金周转速度越快，风险愈小，盈利愈多。

5 结 语

本文从应用需求、经济效益、应用类型和评价指标等方面深入分析了储能优化配置的关键问题。文中的分析结论对储能应用规划具有积极的指导作用。在储能应用实践中，有以下几个方面有待深入研究：

(1)储能自身具有优越的技术性能，结合各种先进的控制策略，使储能应用不再存在技术难题，但是如何在满足技术需求的同时减少储能系统的配置容量是储能规划追求的最终目标；

(2)在各类数字仿真平台搭建储能模型进行时域仿真验证时，一般只考虑储能容量限制对平抑功率波动的影响，而忽略了储能最大充放电功率的限制，而这点也是影响储能性能的重要因素。

[1]张文亮，丘明，来小康.储能技术在电力系统中的应用[J].电网技术，2008，32(7)：1-9.

ZHANG Wenliang，QIU Ming，LAI Xiaokang.Application of energy storage technologies in power grids[J].Power System Technology，2008，32(7)：1-9.

[2]周林，黄勇，郭珂，等.微电网储能技术研究综述[J].电力系统保护与控制，2011，39(7)：147-152.

ZHOU Lin，HUANG Yong，GUO Ke，et al.A survey of energy storage technology for micro grid[J].Power System Protection and Control，2011，39(7)：147-152.

[3]RIBEIRO P F，JOHNSON B K，CROW M L，et al.Energy storage systems for advanced power applications[J].Proceedings of the IEEE，2001，89(12):1744-1756.

[4]赵静波，雷金勇，甘德强.电池储能装置在抑制电力系统低频振荡中的应用[J].电网技术，2008，32(6)：93-99，108.

ZHAO Jingbo，LEI Jinyong，GAN Deqiang.Application of battery energy storage devices in suppressing low-frequency oscillation of power system[J].Power System Technology，2008，32(6)：93-99，108.

[5]马腾宇.超导储能装置(SMES)用于改善电力系统稳定性的布局研究[D].武汉：华中科技大学，2009.

MA Tengyu.Study on the optimal location of Superconducting Magnetic energy storage (SMES) used for improving the transient stability of Power System [D].Wuhan：Huazhong University of Science and Technology，2009.

[6]LIU D B， SHIL J， XU Q，et al.Selection of installing locations of flywheel energy storage system in multi-machine power systems by modal analysis[C]//International Conference on Sustainable Power Generation and Supply.Nanjing，China:IEEE，2009.

[7]UEDA S，TAKEUCHI H，OHSAWA Y.Studies on power system stabilization by distributed allocation of micro SMES units[C]//Proceedings of IEEE Conference on Power System Technology.Kunming，China:IEEE，2002.

[8]LI Y Z，WADA K，OHSAWA Y.Optimal allocation of micro SMES units for power system stabilization by means of genetic algorithm[C]//Proceedings of IEEE Conference on Power System Technology.Chongqing，China:IEEE，2006.

[9]夏亚君.储能提高电力系统暂态稳定性的优化配置研究[D].武汉：华中科技大学，2012.

XIA Yajun.The optimal allocation of energy storage system for enhancing transient stability of power system [D].Wuhan：Huazhong University of Science and Technology，2012.

[10]吴迪，刘世林，文劲宇.一种基于暂态稳定风险的储能位置与容量优化方法[J].电力科学与技术学报，2012，27(1)：19-26.

WU Di，LIU Shilin，WEN Jinyu.A transient stability risk assessment based optimization method[J].Journal of Electric Power Science and Technology，2012，27(1)：19-26.

[11]OHSAWA Y，MARUOKA Y，TAKENO H，et al.Determination of installation location of SMES for power system stabilization[C]//Proceedings of IEEE Conference on Circuits and Systems.Geneva，Switzerland:IEEE，2000.

[12]熊雄，袁铁江，杨水丽，等.基于电压稳定与限值的风/储系统容量配置[J].电网与清洁能源，2012，28(4)：63-68.

XIONG Xiong，YUAN Tiejiang，YANG Shuili，et al.Based on the voltage stability and limit wind-energy storage system capacity configuration[J].Power System and Clean Energy，2012，28(4)：63-68.

[13]李婷婷.需求侧储能提高电网静态安全性的优化配置研究[D].武汉：华中科技大学，2013.

LI Tingting.Optimal configuration of demand side ES for improving the power system Security[D].Wuhan：Huazhong University of Science and Technology，2013.

[14]李红梅，严正.用可再生能源充电的SMES装置在系统调频中的应用[J].电力系统自动化，2009，33(15)：94-97,102.

LI Hongmei，YAN Zheng.Application of renewable energy charged SMES devices in power system frequency regulation[J].Automation of Electric Power Systems，2009，33(15)：94-97,102.

[15]MERCIER P，CHERKAOUI R，OUDALOV A.Optimizing a battery energy storage system for frequency control application in an isolated power system[J].IEEE Transactions on Power Systems，2009，24(3)，1469-1477.

[16]ALEXANDRE O，DANIEL C，CHRISTIAN O.Optimizing a battery energy storage system for primary frequency control[J].IEEE Transactions on Power Systems，2007，22(3):1259-1266.

[17]丁冬.适用于调频的储能系统配置策略研究[D].北京：华北电力大学，2015.

DING Dong.Research on energy storage system configuration strategy for frequency regulation [D].Beijing：North China Electric Power University，2015.

[18]黄际元，李欣然，曹一家，等.考虑储能参与快速调频动作时机与深度的容量配置方法[J].电工技术学报，2015，30(12)：454-464.

HUANG Jiyuan，LI Xiran，CAO Yijia，et al.Capacity allocation of energy storage system considering its action moment and output depth in rapid frequency regulation[J].Transactions of China Electrotechnical Society，2015，30(12)：454-464.

[19]姜书鹏，乔颖，徐飞，等.风储联合发电系统容量优化配置模型及敏感性分析[J].电力系统自动化，2013，37(20)：16-21.

JIANG Shupeng，QIAO Ying，XU Fei，et al.Capacity optimization and sensitivity analysis of cogeneration system of wind power and energy storage[J].Automation of Electric Power Systems，2013，37(20)：16-21.

[20]冯江霞，梁军，张峰，等.考虑调度计划和运行经济性的风电场储能容量优化计算[J].电力系统自动化，2013，37(1)：90-95.

FENG Jiangxia，LIANG Jun，ZHANG Feng，et al.An optimization calculation method of wind farm energy storage capacity[J].Automation of Electric Power Systems，2013，37(1)：90-95.

[21]GUPTA A，SAINIR P, SHARMAM P.Hybrid energy system sizing incorporating battery storage: an analysis via simulation calculation[C]//Proceedings of IEEE Conference on Power System.Kharagpur，Indian:IEEE，2009.

[22]杨水丽，惠东，李建林，等.适用于风电场的最佳电池容量选取的方法[J].电力建设，2010，31(9)：1-4.

YANG Shuili，HUI Dong，LI Jianlin，et al.Selection of the optimal battery capacity for wind farm[J].Electric Power Construction，2010，31(9)：1-4.

[23]张浩，马爱军，李文斌，等.风电场日出力曲线和储能容量关系研究[J].中国电力，2012，45(6)：77-81.

ZHANG Hao，MA Aijun，LI Wenbin，et al.Research of the relationship between wind farm output and energy storage[J].Electric Power，2012，45(6)：77-81.

[24]韩涛，卢继平，乔梁，等.大型并网风电场储能容量优化方案[J].电网技术，2010，34(1)：169-173.

HAN Tao，LU Jiping，QIAO Liang，et al.Optimized scheme of energy storage capacity for grid-connected large-scale wind farm[J].Power System Technology，2010，34(1)：169-173.

[25]毛彪.液流储能对分布式发电系统稳定运行的作用机理及优化配置理论研究[D].武汉：华中科技大学，2012.

MAO Biao.Research on mechanism and optimization theory of the impact of VRB energy storage on stable operation of distributed generation system[D].Wuhan：Huazhong University of Science and Technology，2012.

[26]刘小寨，徐天，葛立坤，等.含风电场的电网储能系统选址和优化配置[J].电网与清洁能源，2014，30(12)：119-125.

LIU Xiaozhai，XU Tian，GE Likun，et al.Location selection and optimal allocation for energy storage system of power system with wind farm[J].Power System and Clean Energy，2012，30(12)：119-125.

[27]李翔.抑制风电电压闪变的混合储能优化配置方法[D].广州：华南理工大学，2013.

LI Xiang.Hybrid energy storage systems for wind power systems: optimization of system capacity and cost through suppress voltage flicker[D].Guangzhou：South China University of Technology，2013.

[28]颜志敏，王承民，连鸿波，等.计及缺电成本的用户侧蓄电池储能系统容量规划[J].电力系统自动化，2012，36(11)：50-54.

YAN Zhimin，WANG Chengmin，LIAN Hongbo，et al.Capacity plan of battery energy storage system in user side considering power outtage cost[J].Automation of Electric Power Systems，2012，36(11)：50-54.

[29]向育鹏，卫志农，孙国强，等.基于全寿命周期成本的配电网蓄电池储能系统的优化配置[J].电网技术，2015，39(1)：264-270.

XIANG Yupeng，WEI Zhinong，SUN Guoqiang，et al.Life cycle cost based optimal configuration of battery energy storage system indistribution network[J].Power System Technology，2015，39(1)：264-270.

[30]肖峻，张泽群，张磐，等.用于优化微网联络线功率的混合储能容量优化方法[J].电力系统自动化，2014，38(12)：19-26.

XIAO Jun，ZHANG Zequn，ZHANG Pan，et al.A capacity optimization method of hybrid energy storage system for optimizing tie-line power in microgrids[J].Automation of Electric Power Systems，2014，38(12)：19-26.

[31]殷志敏，晁勤，王一波，等.波动率优于国网标准的风电场储能容量经济优化配置[J].可再生能源，2016，32(1)：86-94.

YIN Zhimin，CHAO Qin，WANG Yibo，et al.An economic optimal method for wind farm energy storage capacity with superior fluctuation rate to standard of the State Grid[J].Renewable Energy Resources，2016，32(1)：86-94.

[32]谢石骁，杨莉，李丽娜.基于机会约束规划的混合储能优化配置方法[J].电网技术，2012，36(5)：79-84.

XIE Shixiao，YANG Li，LI Lina.A chanceconstrained programming based optimal configuration method of hybrid energy storage system[J].Power System Technology，2012，36(5)：79-84[33]黎静华，文劲宇，程时杰，等.基于p-有效点理论的含大规模风电电力系统最小储能功率配置方法[J].中国电机工程学报，2013，33(13)：45-52.

LI Jinghua，WEN Jinyu，CHENG Shijie，et al.Method of minimum energy storage power allocation for electric power systems with large-scale wind power based on p-efficient point theory[J].Proceedings of the CSEE，2013，33(13)：45-52.

[34]HIDA Y，ITO Y，YOKOYAMA R, et al.A study of optimal capacity of PV and battery energy storage system distributed in demand side[C]//Universities Power Engineering Conference (UPEC).Cardiff，Wales:IEEE，2010.

[35]张峰，董晓明，梁军，等.考虑目标分解及其互补平抑的风电场复合储能容量优化[J].电力系统自动化，2014，38(7)：9-15.

ZHANG Feng，DONG Xiaoming，LIANG Jun，et al.Capacity optimization of hybrid energy storage system based on target decomposition and complementary fluctuations smothing[J].Automation of Electric Power Systems，2014，38(7)：9-15.

[36]李成，杨秀，张美霞，等.基于成本分析的超级电容器和蓄电池混合储能优化配置方案[J].电力系统自动化，2013，37(18)：20-24.

LI Cheng，YANG Xiu，ZHANG Meixia，et al.Optimal configuration scheme for hybrid energy storage system of super—capacitors and batteries based on cost analysis[J].Automation of Electric Power Systems，2013，37(18)：20-24.

[37]马速良，蒋小平，马会萌，等.平抑风电波动的混合储能系统的容量配置[J].电力系统保护与控制，2014，42(8)：108-114.

MA Suliang，JIANG Xiaoping，MA Huimeng，et al.Capacity configuration of the hybrid energy storage system for wind power smoothing[J].Power System Protection and Control，2014，42(8)：108-114.

[38]熊雄，叶林，杨仁刚，等.多元复合储能在独立微电网中运行策略及容量优化研究[J].智能电网，2014，2(6)：5-10.

XIONG Xiong，YE Lin，YANG Rengang，et al.Operation strategy and capacity optimization of multi-element composite energy storage system in stand-alone microgrid[J].Smart Grid，2014，2(6)：5-10.

[39]高孝天，凌志斌，郭海峰，等.基于粒子群优化的风储配合控制策略研究[J].太阳能学报，2014，35(11)：2249-2256.

GAO Xiaotian，LING Zhibin，GUO Haifeng，et al.Control strategies for wind farm with battery energy storage based on particle swarm optimization[J].Acta Energiae Solaris Sinica，2014，35(11)：2249-2256.

[40]ZHONG Qing，YU Nanhua，ZHANG Xiaoping，et al.Optimal siting&sizing of battery energy storage system in active distribution network[C]//IEEE/PES Innovation Smart Grid Technologies Europe.Lyngby，Denmark:IEEE，2013.

[41]瞿海妮，刘建清.国内外配电网供电可靠性指标比较分析[J].华东电力，2012，40(9)：1566-1570.

QU Haini，LIU Jianqin.Comparison and analysis on power supply reliability indicators of distribution network at home and abroad[J].East China Electric Power，2012，40(9)：1566-1570.

[42]谭兴国，王辉，张黎，等.微电网复合储能多目标优化配置方法及评价指标[J].电力系统自动化，2014，32(8)：7-14.

TAN Xingguo，WANG Hui，ZHANG Li，et al.Multi-objective optimization of hybrid energy storage and assessment indices in microgrid[J].Automation of Electric Power Systems，2014，32(8)：7-14.

[43]杨毅，刘洁，于建成，等.分布式储能优化配置影响因素的评价方法研究[J].现代电子技术，2015，38(2)：152-157.

YANG Yi，LIU Jie，YU Jiancheng，et al.Evaluation method of distributed energy storage system in consideration of optimizationconfiguration influence factors[J].Modern Electronics Technique，2015，38(2)：152-157.

(编辑 张小飞)

Principal Problems of Energy Storage Optimization Allocation

LI Dandan, SU Xiaolin, YAN Xiaoxia, TAN Yixue

(Department of Electric Power Engineering,Shanxi University,Taiyuan 030013,China)

Energy storage optimization allocation is the foundation of energy storage system (ESS) application, which involves two dimensions of technical and economic aspects, also relates to the different needs of multi-application time scales and power energy.According to the different application requirements of ESS in power grids, focusing on security and stability, frequency regulation, acceptance of renewable energy sources and power quality, this paper analyzes the optimal allocation of its objectives, conditions, methods and theories deeply.Based on the cost-benefit analysis of energy storage system, this paper establishes a general NPV (net present value) optimization model.Combined with the application characteristics of different energy storage, this paper analyzes the selection principles of energy storage type, as well as the combination type of composite energy storage and the methods of capacity allocation.This paper presents the relevant evaluation index and methods for the evaluation of energy storage application from the compensation effect, safety, reliability, economy and so on.Finally, this paper proposes the future research topics in the practice of energy storage planning.

energy storage; electric power system; optimization allocation; evaluation index

TM 910

A

1000-7229(2016)09-0070-09

10.3969/j.issn.1000-7229.2016.09.010

2016-05-12

李丹丹(1992)，女，硕士研究生，研究方向为电力系统稳定分析与控制、储能技术；

苏小林(1963)，男，工学博士，教授，本文通讯作者，主要研究方向为电力系统运行与控制、智能电网等；

阎晓霞(1963)，女，工学学士，副教授，研究方向为电力系统运行与控制；

谭逸雪(1992)，女，硕士研究生，研究方向为储能在电力系统中的应用。