计及需求响应的含风电场日前两阶段动态环境经济调度

刘旭，杨德友，孟涛，张旺，刘曦，姜明磊

(1.东北电力大学电气工程学院，吉林省吉林市 132012；2.国网吉林省电力有限公司电力科学研究院，长春市 130021；3.国网吉林省电力有限公司经济技术研究院，长春市 130000)

计及需求响应的含风电场日前两阶段动态环境经济调度

刘旭1，杨德友1，孟涛2，张旺1，刘曦3，姜明磊3

(1.东北电力大学电气工程学院，吉林省吉林市 132012；2.国网吉林省电力有限公司电力科学研究院，长春市 130021；3.国网吉林省电力有限公司经济技术研究院，长春市 130000)

需求响应作为发电侧与需求侧之间的重要互动资源，能有效调节负荷需求分布来实现节能减排和提高系统风电接纳能力的目的。基于此，将需求响应融入环境经济中，提出一种智能电网下的日前两阶段调度模型：第1阶段为日前用户互动阶段，通过分时电价的杠杆作用引导用户理性用电，以调整次日负荷需求分布，综合考虑负荷水平和用户用电满意度确定最优负荷曲线和分时电价；第2阶段为日前调度阶段，针对风电出力随机性，建立基于机会约束规划的环境经济调度模型，采用风电出力分布函数将其转化为确定性模型。将种群多样性指标和随机黑洞理论引入粒子群算法中，结合多目标搜索机制，提出一种改进多目标粒子群算法对模型求解，并采用逼近理想解排序法(technique for order preference by similarity to ideal solution，TOPSIS)对Pareto前沿个体排序，辅助调度人员进行科学决策。改进10机系统的仿真结果验证了该模型及方法的有效性与合理性。

风电；需求响应；分时电价；用户满意度；环境经济调度；逼近理想解排序法(TOPSIS)

0 引 言

日益加剧的环境污染和能源枯竭促进了风、光等清洁能源的发展。风力发电因安装方式灵活、低碳环保、便于维护等优势获得了国内外广泛的关注，并逐渐取代传统化石能源成为国家能源战略布局中的重要组成部分[1]。然而，大规模风电并网运行增加了系统运行的复杂性和不确定性，对电力系统优化调度提出了更高的要求与挑战[2]。

传统电力系统经济调度是在满足功率平衡、旋转备用和机组出力极限等约束下，合理安排负荷分配使发电成本最小，但随着风电并网容量的逐渐增大，从经济、技术和环保等多方面综合展开电力系统经济调度问题的研究更加符合当前能源发展趋势。文献[3]建立了含风电场环境的经济调度随机模型，考虑风电出力随机性对系统旋转备的影响，应用改进多目标差分进化算法对模型求解，但忽略了系统网损。文献[4]兼顾系统运行经济性与环境效益，建立含风电场多目标动态环境经济调度(dynamic economic emission dispatch，DEED)模型，但没有考虑机组的启停费用。文献[5]针对风电出力随机性的特点，应用多场景理论建立计及污染气体排放风险的DEED模型，对污染气体排放风险进行有效管理，但仅考虑在不同风电出力场景下的调度计划，并不能全面分析风电出力随机性对系统调度的影响。以上文献仅从优化发电侧资源的角度进行DEED的研究，但发电侧资源十分有限，并不能满足低碳环保的电力发展要求。

需求响应作为电力市场框架下的重要互动资源，能有效引导终端用户采取合理的用电方式和用电结构，以调整负荷需求分布，应对风电出力随机性和反调峰特性。文献[6]建立计及需求响应的含风电场经济环境联合调度模型，采用线性权重法将多目标转化为单目标，这种简化虽然降低了求解难度，但不能深入挖掘各目标函数间的内在联系，在最终决策时将面临选择单一的局面。文献[7]引入分时电价(time-of-use price，TOU)及可中断负荷这2种响应形式，针对风电场出力的随机特性，从运行可靠性的角度整合系统资源，有效提高了风电利用率，但没有计及污染气体排放对调度结果所造成的影响。文献[8]构建基于电力需求弹性理论的用户不确定响应模型，应用实时电价引导终端用户合理用电，但需求弹性矩阵的建立需要分析大量市场数据，实现起来具有一定难度。

针对以上问题，本文将需求响应融入DEED中，从负荷水平、用户用电满意度、系统运行经济性和环境效益的角度，建立日前两阶段优化调度模型，将发电侧与需求侧资源整合统一调度，以协调风电入网和实现削峰填谷的目的。提出一种改进多目标粒子群算法(improved multi-objective particle swarm optimization algorithm，IMPSO)对模型求解，并应用辅助决策—逼近理想解排序法(technique for order preference by similarity to ideal solution，TOPSIS)对Pareto前沿个体排序，辅助调度人员确定最佳调度方案。

1 风电出力随机模型

大量风速数据的统计分析表明，双参数威布尔(Weibull)分布能较准确描述实际风速的变化规律，其分布函数为

F(v)=1-exp[-(v/c)k]

(1)

式中：k为形状参数；c为尺度参数；v为风速。其概率密度函数为

f(v)=(k/c)(v/c)k-1exp[-(v/c)k]

(2)

当知道风速分布后，通过分析风电功率输出和风速的关系可得到二者近似的随机分布。图1给出了风电机组功率输出和风速的函数关系，其中，Prate为额定输出功率，vin、vout和vrate分别为切入风速、切出风速和额定风速。

图1 风力发电功率输出曲线Fig.1 Power output curve of wind energy system

由图1可知，风力发电的输出功率Pwind与风速v的函数关系可表示为

(3)

由式(3)可知，Pwind在(0,Prate)区间上连续，而在区间端点0和Prate处离散，即Pwind是一个混合随机变量，其分布函数[9]可表示为

(4)

2 DR对DEED的影响

2.1 用户不确定响应行为建模

电价作为影响用户用电行为的主导因素，较激励型的需求响应更能体现用户消费的主观意识。由消费者心理学原理[10]可知，用户对电价刺激的响应行为分为3种，即不敏感区(相当于死区)，此时电价波动(峰平谷各时段电价差)较小，用户各时段用电量几乎不变；正常响应区(相当于线性区)，此时用户根据各时段电价变化情况合理调整用电方式，以尽可能追求电费最小；响应极限区(相当于饱和区)，此时电价波动较大，超出了用户响应极限，用户各时段用电量将不随电价波动而改变。

为确定实施TOU后的系统负荷，首先引入负荷转移率概念，负荷转移率是指负荷由高电价时段向低电价时段的转移量与高时段负荷的比值，描述的是各时段负荷随电价波动的转移情况。由实际数据分析可知，负荷转移率与电价波动的关系可采用分段线性函数表示。以峰时段到谷时段的负荷转移率曲线为例，如图2所示，其中横坐标表示峰、谷电价差，纵坐标表示负荷转移率。

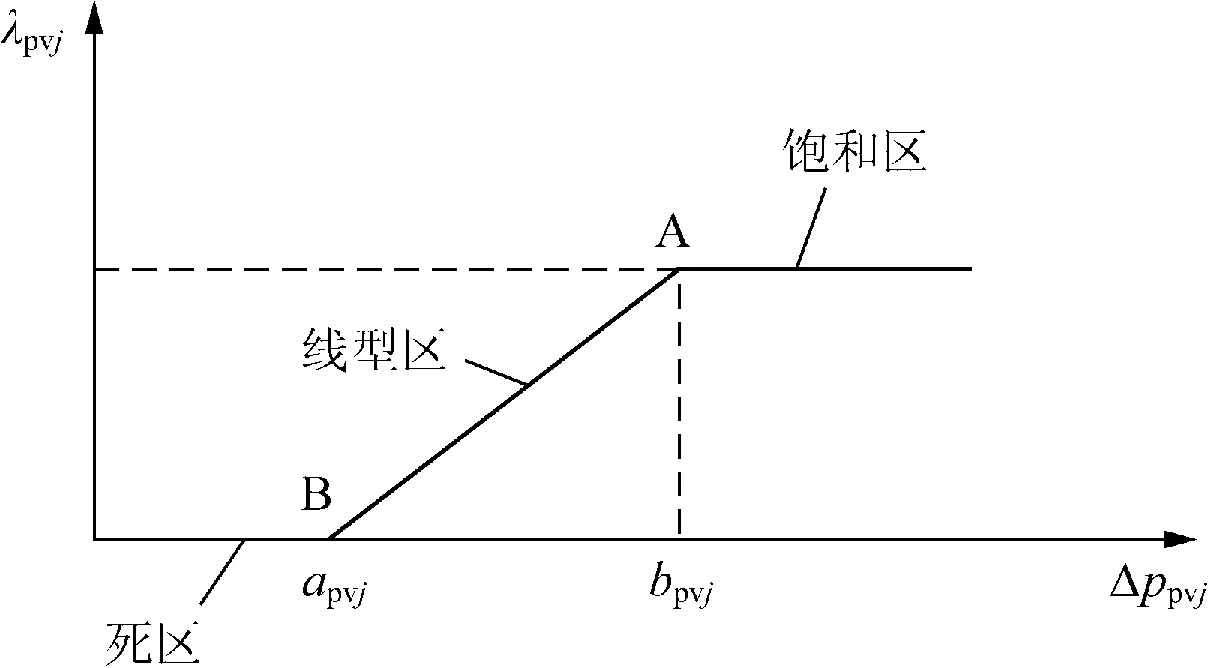
图2 峰时段到谷时段的负荷转移率曲线Fig.2 Load shifting curve from peak to valley

峰时段到谷时段的负荷转移率为

(5)

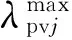
实行TOU后的j类用户各时段拟合负荷为

(6)

2.2 用户满意度

用户满意度属于市场营销范畴的概念。用户通过TOU的引导参与次日负荷曲线的制定，较高的峰谷电价比会使用户响应充分，有效提高系统负荷水平，达到削峰填谷的目的，但同时也会使用户的用电方式和用电结构发生大幅度改变，使用户对TOU的实施产生抵触情绪，损害电力公司的社会形象。然而，较低的峰谷电价比又达不到电力公司理想的预期效果。因此，有必要综合考虑用户和电力公司双方的利益来制定TOU和负荷曲线，寻求二者的利益均衡。本文将文献[11]中2个用户满意度指标引入DEED中，作为影响TOU及负荷曲线制定的约束条件，以保证最终调度方案使用户满意。

电费支出满意度是描述TOU实施前后用户电费支出的变化情况，如式(7)：

(7)

式中：p0、pt分别为实施TOU前后的t时段电价。ρ≥1表示用户电费支出有所减少，用户从TOU实施中获益，反之用户利益受损。

用电方式满意度是描述TOU实施前后用户各时段用电量的变化情况，如式(8)：

(8)

由式(8)可知，θ是介于[0，1]之间的数，当θ=1时，用电方式满意度最大，即用户的用电方式和用电结构没有发生任何改变。

3 计及需求响应的日前两阶段多目标DEED模型

3.1 日前用户互动模型

在日前用户互动阶段，综合考虑用户和电力公司双方利益，优化TOU来制定最优的负荷曲线。以负荷均方差为目标函数，如式(9)：

(9)

式中：PD,t为t时段系统负荷，与常规优化调度不同的是此时负荷是受TOU影响的变量。

用户互动模型的约束条件可概括为以下几点。

(1)用户满意度约束：

(10)

式中：θmin为电费支出满意度下限；λmin为用电方式满意度下限。

(2)采用峰时电价与谷时电价拉开幅值不等的方式，固定平时段电价为实施TOU前的原始电价，为保证实施TOU前后的负荷峰谷特性不变，则拉开比ω需满足[12]：

(11)

式中：Qp为峰时段总用电量；Qv为谷时段总用电量。

3.2 日前调度模型

基于日前用户互动阶段得到的最优负荷曲线，在日前调度阶段，根据次日风电预测出力和火电机组的工作状态，综合考虑系统运行经济性和环境效益，建立基于机会约束规划的多目标调度模型，目标函数如下所述。

(1)发电总费用。常规火电机组的发电总费用目标函数为

(12)

式中：N为火电机组台数；Ui,t为第i台火电机组t时段的工作状态，Ui,t=1表示第i台火电机组处于开机状态，Ui,t=0表示第i火电机组处于停机状态；Ci,t(Pi,t)为第i台火电机组t时段燃料成本；Pi,t为第i台火电机组t时段输出有功功率；Si,t为第i台火电机组t时段启停动成本。

火电机组的燃料成本采用二次函数表示：

(13)

式中：ai、bi、ci为第i台火电机组燃料费用参数。

火电机组启停成本与各机组运行状态和初始状态有关：

(14)

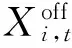
(2)污染气体排放量。常规火电机组消耗化石能源会产生CO2、SOx、NOx等污染气体，考虑污染气体综合排放量的目标函数[13]为

(15)

式中：αi、βi、γi、λi、ξi为第i台火电机组污染气体排放特性参数。

日前调度模型的约束条件如下。

(1)功率平衡约束：

(16)

式中：Pw,t为风电场t时段输出有功功率；PD,t为实施TOU后t时段系统负荷；Ploss,t为t时段网络损耗，通过B系数法获得：

(17)

式中：Bij、Bi0、B00为网络损耗系数。

由于Pw,t为随机变量，采用机会约束以概率的形式将式(16)表示为

(18)

式中：Pr{·}为满足{·}事件的置信水平；μ为满足功率平衡约束的置信水平下限。

(2)风电渗透率极限约束：

抢抓银监会下放村镇银行准入权限到省银监局的政策机遇。2018年起，开展组建村镇银行工作，鼓励现有村镇银行向农村地区延伸，不断提高服务“三农”水平，夯实经营基础；支持和鼓励村镇银行通过增资扩股做大、做强，改善村镇银行外部结算环境和社会公信力；探索适合当地实际的农村资金互助社试点模式；出台市级供销合作社系统社员股金服务机构监督管理办法，规范发展基层新型供销社社员股金服务业务，使其成为服务“三农”的重要补充，逐步形成不同类型、不同规模、互补性强的农村金融组织体系，为农村经济社会发展和脱贫攻坚提供多元化、差异化、特色化的金融服务。

Pw,t≤δPD,t

(19)

式中：δ为风电渗透率极限系数。采用机会约束以概率的形式将式(19)表示为

Pr{δPD,t≥Pw,t}≥φ

(20)

式中：φ为满足风电穿透极限约束的置信水平下限。

(3)火电机组出力约束：

Pi,min≤Pi,t≤Pi,max

(21)

式中：Pi,min、Pi,max分别为第i台火电机组出力上、下限。

(4)火电机组最小启停时间约束：

(22)

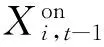
(5)风电场出力约束：

0≤Pw,t≤Pw,max

(23)

式中：Pw,max为风电场出力上限。

(6)系统正、负旋转备用容量约束：

(24)

(25)

3.3 随机模型的确定化

将随机模型转化为等价的确定性模型是求解机会约束规划问题的常用方法。式(18)、(20)均包含随机变量Pw,t，结合Pw,t分布函数式(4)，可将式(18)转化为

(26)

将式(4)代入式(26)，整理可得到：

(27)

同理，式(20)可转化为

(28)

综上分析，确定性日前多目标调度模型为

(29)

式中：P为由各火电机组出力变量构成的集合；g(·)为不等式约束条件。

4 改进多目标粒子群算法

4.1 粒子群算法回顾

vid(t+1)=ωvid(t)+c1r1[pid-xid(t)]+c2r2[pgd-xid(t)]

(30)

xid(t+1)=xid(t)+vid(t+1)

(31)

式中：t为当前搜索代数；vid(t)和xid(t)分别为粒子i速度和位置的d维分量；pid为粒子i历史最优位置的d维分量；pgd为种群历史最优位置的d维分量；ω为惯性系数；c1和c2为学习因子；r1，r2为[0，1]区间内的均匀分布随机数。

4.2 改进多目标粒子群算法

4.2.1 自适应惯性权重

在PSO算法中，ω采用线性递减策略，然而该策略并不能充分挖掘将当前种群搜索信息并反馈到下一次迭代中，这往往会导致种群多样性降低，算法陷入局部最优，早熟收敛。针对这一问题，提出一种基于种群多样性反馈的自适应惯性权重：

(32)

式中：γ为很小的正数；Kmax为总迭代次数；d(t)为种群多样性指标[14]：

(33)

式中：Npop为粒子总数；|L|为搜索空间最大对角距离；D为优化问题维数；pd(t)为种群位置的d维分量平均值。

4.2.2 随机黑洞机制的引入

文献[15]将黑洞演化过程中的星体运动理论引入PSO算法中，提出一种随机黑洞粒子群算法(RBH-PSO)。在RBH-PSO算法中，将每次搜索到的种群最优位置的d维分量pgd为中心，在以r为半径的区域内随机产生一粒子为黑洞，粒子以一定的概率被黑洞捕获，在进入黑洞后也有一定概率的逃离黑洞，进而增加粒子探索新区域的可能，提高算法的勘探能力。本文将RBH-PSO算法扩展应用到DEED求解中，图3给出粒子位置更新示意图。

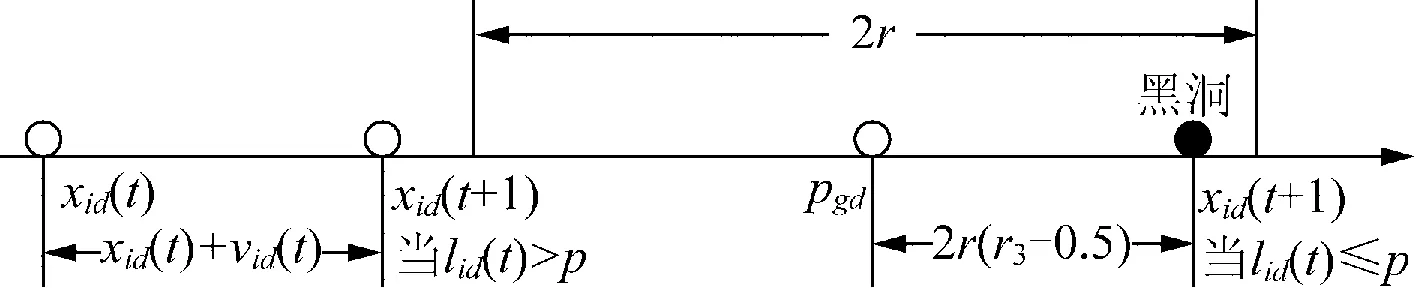
图3 粒子位置更新示意图Fig.3 Schematic diagram of particle position

由图3可知：当lid>p时，粒子脱离黑洞引力范围，按传统方式更新粒子位置，否则粒子被黑洞捕获，位置更新方式如下：

(34)

式中：p为黑洞捕获粒子的概率阈值，是介于[0，1]之间的定常数；lid(t)为xid(t)对应的概率值，是服从[0，1]区间均匀分布的随机数；r3为服从[0，1]区间均匀分布的随机数，表示粒子进入黑洞后，也有一定概率逃离黑洞。

4.2.3 多目标优化

为使改进PSO算法适用于求解多目标优化问题，在算法搜索过程中引入累积排序操作和精英保留操作，并采用文献[16]中改进的拥挤距离操作，以获得分布广泛均匀地Pareto前沿。粒子A和粒子C之间的粒子B的拥挤距离如式(35)：

min[|fi(A)-fi(B)|,|fi(B)-fi(C)|]}

(35)

式中：Nobj为目标出数的个数；fi(A)表示粒子A第i个目标函数的适应度值。

4.3 辅助决策

多目标优化问题的各子目标函数存在相互竞争的关系，优化得到的Pareto前沿包含丰富解的信息，为辅助决策者直观、快速的制定调度方案，本文采用TOPSIS[17]对Pareto前沿个体进行排序，排序结果客观地反映各调度方案的优劣。在应用TOPSIS法对

Pareto前沿个体排序时，首先需要确定各属性的权重集，本文采用信息熵法来获得。

5 算例分析

5.1 算例描述

对含1个并网风电场和10台燃煤机组的电力系统为例进行两阶段环境经济调度计算，系统负荷及机组耗量特性参数见文献[18]，污染气体排放参数见文献[19]。并网风电场含有60台风机，每台风机的额定功率为2 MW，切入风速、切出风速和额定风速分别为4.3，7.7和17.9 m/s，1天内各时段形状参数与尺度参数参照文献[20]取值。

5.2 计及DR的两阶段调度结果分析

5.2.1 日前用户互动模型结果分析

实施TOU前的原始电价为0.8 元/(kW·h)，峰平谷各时段划分见文献[21]。调度周期为1天，以1 h为单位分为24个时段。采用专业的优化软件CPLEX对日前用户互动模型进行求解，表1给出了几种典型优化方案的结果。

表1 日前用户互动阶段的典型优化方案
Table 1 Typical optimization scheme of day-ahead user interaction stage

从表1可知：负荷均方差随着拉开比的增大而减小，两者呈明显的负相关趋势，这是由于拉开比可以调节峰谷电价差，拉开比越大用户对TOU的响应越充分，削峰填谷的作用就越明显。未考虑需求响应时，负荷曲线的峰谷差为800 MW，最优解较其降低了337 MW，可见引入需求侧资源可以显著改善系统负荷水平，有效避免了因负荷显著波动给系统运行带来的安全问题，图4给出了计及需求响应前后的负荷曲线；电费支出满意度均大于1，说明实施TOU后的用户电费支出有所减少，这符合TOU的制定原则，即TOU的实施以不损害用户的利益为前提，同时可以看出电费支出满意度又接近于1，说明本文电价方案并没有严重影响电网公司的盈利；用电方式满意度均较大，说明TOU的实施没有给用户的用电方式和用电结构带来大幅度的改变，同时可以看出用电方式满意度与拉开比呈负相关趋势，这是由于拉开比越大，峰谷电价差越大，用户为了追求用电费用最小，被迫改变用电方式。综上分析可知，本文方法得到的电价

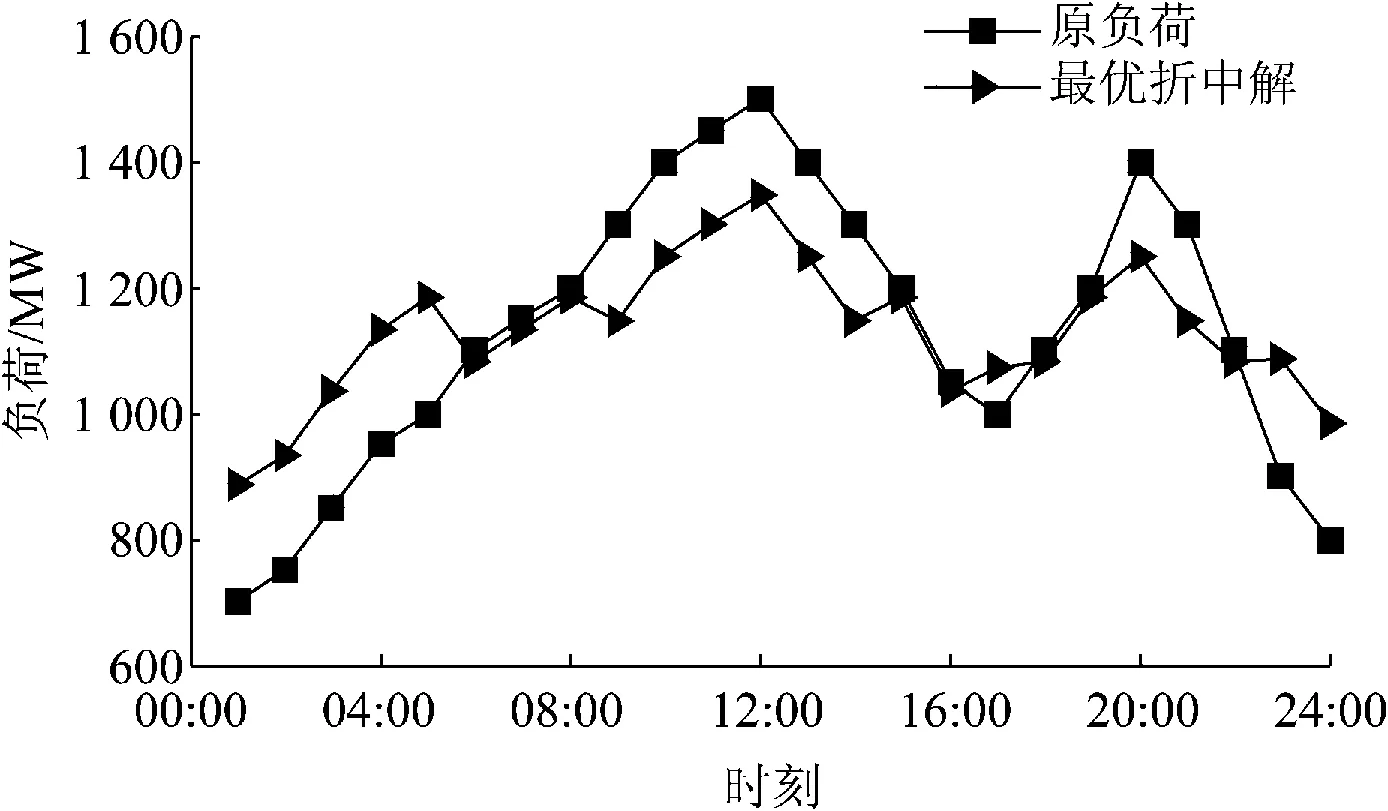
图4 计及需求响应前后负荷曲线Fig.4 Load curves with or without considering demand response

方案和次日负荷曲线兼顾了用户和电网公司双方的利益，为调度决策者提供一定的理论参考。

5.2.2 日前调度模型结果分析

风电场24 h预测出力曲线见图5，风电的渗透率极限δ=7%，正、负旋转备用容量均取各时段系统负荷的5%。置信水平μ、φ分别为0.95和0.85。IMPSO算法参数设置：粒子种群规模Npop=100；最大迭代次数Kmax=100次；学习因子c1=c2=2；黑洞半径r=0.01；概率阈值p=0.3。为验证IMPSO算法性能，同时采用NSGA-II算法对模型求解，NSGA-II算法的交叉算子指数和交叉率分别为20和0.9，变异算子指数和变异率分别为20和0.025，迭代次数和种群规模与本文一致。2种算法对日前调度模型优化得到Pareto前沿如图6所示。

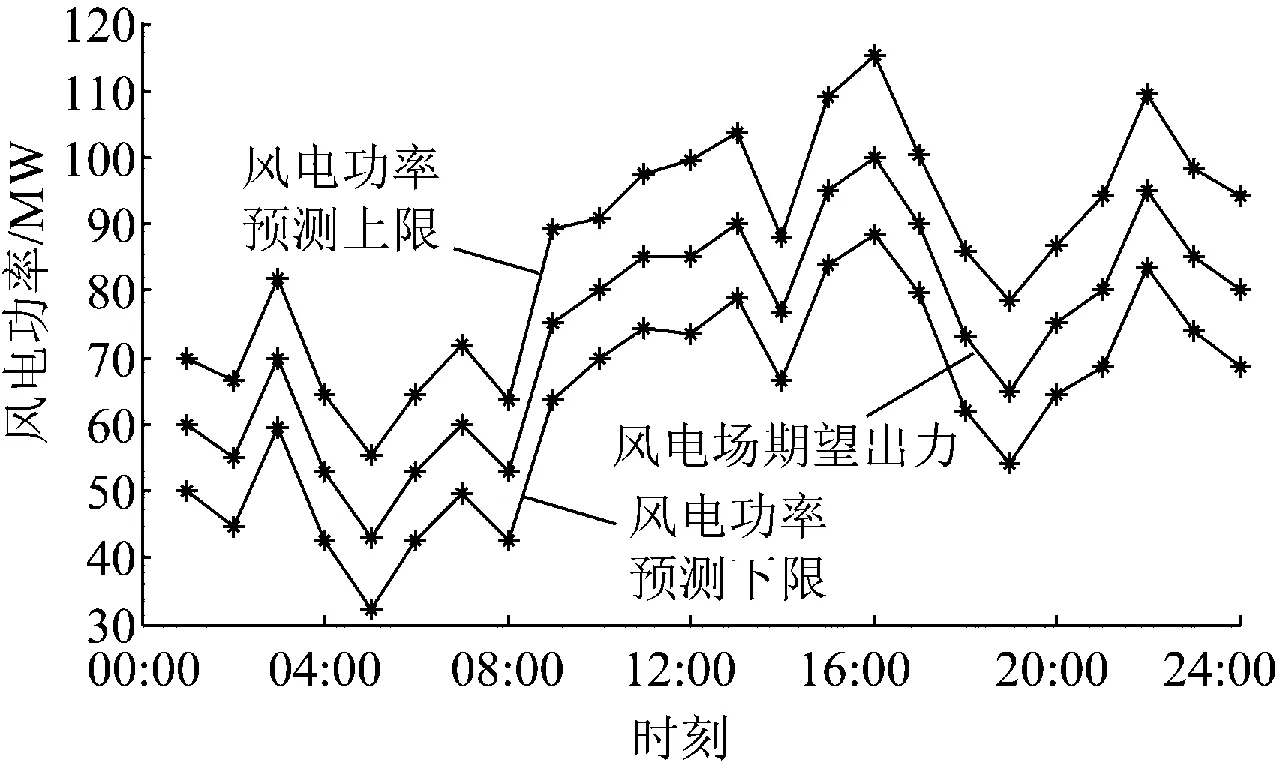
图5 各时段风电场出力及波动区间Fig.5 Hourly wind power and rang of power fluctuating

图6 2种优化算法的Pareto前沿Fig.6 Pareto frontier of two optimal algorithms

从图6可知：与NSGA-II算法相比，IMPSO算法获得的非劣解集分布广泛均匀，更加靠近真实的Pareto前沿，这主要由于自适应惯性权重及随机黑洞机制的引入，提高了种群多样性，均衡了算法全局和局部搜索性能。结合图5、6分析可知，由于各时段风电场出力相近，负荷在各火电机组间随机分配，导致Pareto前沿个体的发电成本与污染气体排放量差别较大，这无疑增加了调度人员的决策难度，而采用TOPSIS法对Pareto前个体进行排序，排序结果直观反映了各发电计划优劣，便于调度人员进行科学的决策。2种算法极端解及最优解的各个指标见表2。

表2 日前调度阶段的Pareto多样性解
Table 2 Pareto multi-solutions of day-ahead dispatch stage

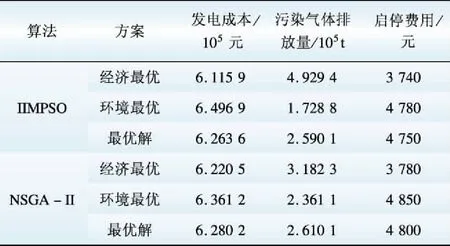
从表2可知：与NSGA-II算法相比，IMPSO算法的极端解和最优解都有所改进；经济最优时启停费用最小，环境最优时启停费用最大，启停费用与发电成本和污染气体排放量呈明显的正、负相关趋势，这与实际的发电情况相符。

5.3 调用需求侧资源前后的结果分析

为进一步验证需求侧资源对DEED的影响，与常规调度模式的优化结果进行比较，2种调度模式下的优化结果如表3所示。图7分别给出了2种调度模式下最优解各时段排污特性曲线和风电并网功率曲线。

表3 常规调度模式和本文模式下的优化结果
Table 3 Optimal solution under conventional dispatching mode and proposed mode

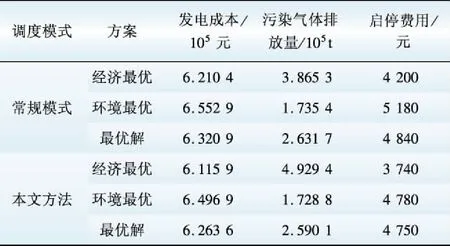
从表3可知：常规调度的经济最优和环境最优分别为6.210 4×105元、1.735 4×105t，而调用需求侧资源时的经济最优与环境最优分别为6.115 9×105元、1.728 8×105t，即发电成本与污气排放量分别减少了0.094 5×105元、0.006 6×105t；最优解的发电成本与污气排放量也分别减少了0.057 3×105元、0.041 6×105t。在启停费用方面，本文方法较常规调度的启停费用有所减少，分析原因是由于TOU的调节作用使负荷曲线趋于平坦，减少了火电机组的启停次数。从图7(a)可知，本文方法并非每个时段的污染气体排放量都小于常规调度，但在总排放量上优势明显。从图7(b)可知，由于用户对负荷分布的调节作用有限，在某些时段的风电并网功率相同，但就总的风电接入量而言，本文方法的风电接入量高于传统调度调度模式。综上分析可知，需求侧资源参与DEED对降低系统运行成本，提高环境效益及风电利用率都非常有利。

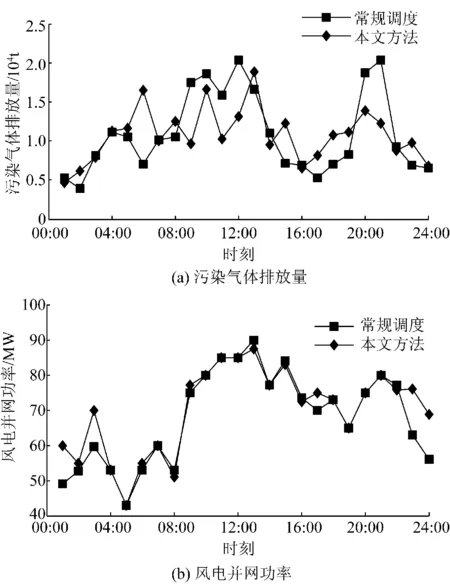
图7 常规调度模式和本文模式下

6 结 论

(1) 本文提出的两阶段调度模型通过需求响应实现了用户信息与电能的双向互动，将供需侧资源整合统一调度以协调配合风电入网。算例分析表明，联合调度供需侧资源可以有效降低发电成本和污染气体排放量，提高系统负荷水平和风电消纳能力。

(2)从决策者的角度，综合考虑了系统负荷水平、用户满意度、环境和经济等多个方面，较全面分析了影响DEED的因素，改变了传统一味地考虑经济性的调度模式。

(3)自适应惯性权重和随机黑洞机制的引入，提高了IMPSO的寻优性能，使得到的Pareto前沿完整性好，非劣解集分布广泛均匀。采用TOPSIS法对Pareto前个体进行排序，辅助决策者制定科学的调度方案，避免了决策盲目性。

[1]李军军，吴政球，谭勋琼，等.风力发电及其技术发展综述[J].电力建设，2011，32(8)：64-72.

LI Junjun, WU Zhengqiu, TAN Xunqiong, et al.Review of wind power generation and relative technology development[J].Electric Power Construction, 2011, 32(8): 64-72.

[2]刘吉臻，王海东，李明扬.含风电的电力系统机组组合问题研究综述[J].电力建设，2014，35(12)：38-45.

LIU Jizhen, WANG Haidong, LI Mingyang.Review on unit commitment of power systems with wind power integration[J].Electric Power Construction, 2014, 35(12): 38-45.

[3]邱威，张建华，刘念.含大型风电场的环境经济调度模型与解法[J].中国电机工程学报，2011，31(9)：8-16.

QIU Wei, ZHANG Nianhua, LIU Nian.Model and solution for environmental/economic dispatch considering large-scale wind power penetration[J].Proceedings of the CSEE, 2011, 31(9): 8-16.

[4]朱永胜，王杰，瞿博阳，等.含风电场的多目标动态环境经济调度[J].电网技术，2015，39(5)：1315-1322.

ZHU Yongsheng, WANG Jie, QU Boyang, et al.Multi-objective dynamic economic emission dispatching of power grid containing wind farms[J].Power System Technology,2015,39(5)：1315-1322.

[5]文旭，王俊梅，郭琳，等.计及污染气体排放风险的多目标随机动态环境经济调度模型[J].电力自动化设备，2015，35(5)：131-138.

WEN Xu, WANG Junmei, GUO Lin, et al.Multi-objective stochastic and dynamic model of environmental and economic dispatch considering gas pollution emission risk[J].Electric Power Automation Equipment, 2015, 35(5): 131-138.

[6]刘晓，艾欣，彭谦.计及需求响应的含风电场电力系统发电与碳排放权联合优化调度[J].电网技术，2012，36(1)：213-218.

LIU Xiao, AI Xin, PENG Qian.Optimal dispatch coordinating power generation with carbon emission permit for wind farms integrated power grid considering demand response[J].Power System Technology, 2012, 36(1): 213-218.

[7]王蓓蓓，刘小聪，李扬.面向大容量风电接入考虑用户侧互动的系统日前调度和运行模拟研究[J].中国电机工程学报，2013，33(22)：35-44.

WANG Beibei, LIU Xiaocong, LI Yang.Day-ahead generation scheduling and operation simulation considering demand respond in large-capacity wind power integrated systems[J].Proceedings of the CSEE, 2013, 33(22): 35-44.

[8]别朝红，胡国伟，谢海鹏，等.考虑需求响应的含风电电力系统的优化调度[J].电力系统自动化，2014，38(13)：115-120.

BIE Chaohong, HU Guowei, XIE Haipeng, et al.Optimal dispatch for wind power integrated systems considering demand response[J].Automation of Electric Power Systems, 2014, 38(13): 115-120.

[9]LIU X, XU W.Economic load dispatch constrained by wind power availability: A here-and-now approach[J].IEEE Transactions on Sustainable Energy, 2010, 1(1): 2-9.

[10]孙宇军，李扬，王蓓蓓，等.计及不确定需求响应的日前调度计划模型[J].电网技术，2014，38(10)：2708-2714.

SUN Yujun, LI Yang, WANG Beibei, et al.A day-ahead scheduling model considering demand response and its uncertainty[J].Power System Technology, 2014, 38(10): 2708-2714.

[11]丁伟，袁家海，胡兆光.基于用户价格响应和满意度的峰谷分时电价决策模型[J].电力系统自动化，2005，29(20)：10-14.

DING Wei, YUAN Jiahai, HU Zhaoguang.Time-of-use price decision model considering user reaction and satisfaction index[J].Automation of Electric Power Systems, 2005, 29(20): 10-14.

[12]胡福年，汤玉东，邹云.需求侧实行峰谷分时电价策略的影响分析[J].电工技术学报，2007，22(4)：168-174.

HU Funian, TANG Yudong, ZOU Yun.Analysis of impacts of TOU price strategy [J].Transactions of China Electrotechnical Society, 2007, 22(4): 168-174.

[13]BAYON L, GRAU J M, RUIZ M M, et al.The exact solution of the environmental/economic dispatch problem[J].IEEE Transaction on Power Systems, 2012, 27(2): 723-731.

[14]YANG Y P, CHE Y H.A diversity guided particle swarm optimization with chaotic mutation[C] // 2nd International Asia Conference on Informatics in Control.Wuhan: IEEE, 2010: 294-297.

[15]ZHANG Junqi, LIU Kun, TAN Ying, et al.Random black hole particle swarm optimization and its application[C] // 2008 IEEE International Conference on Neural Networks and Signal Processing.Nanjing, China: IEEE, 2008: 359-365.

[16]PENG Chunhua, SUN Huijuan, GUO Jianfeng, et al.Multi-objective optimal strategy for generating and bidding in the power market[J].Energy Conversion and Management, 2012(57): 13-22.

[17]徐玖平，吴巍.多属性决策的理论与应用[M].北京：清华大学出版社，2006：45-48.

[18]张宁，胡兆光，周渝慧，等.考虑需求侧低碳资源的新型模糊双目标机组组合模型[J].电力系统自动化，2014，38(17)：25-30.

ZHANG Ning, HU Zhouguang, ZHOU Yuhui, et al.A novel fuzzy bi-objective unit commitment model considering demand side low-carbon resources[J].Automation of Electric Power Systems, 2014, 38(17): 25-30.

[19]BASU M.Dynamic economic emission dispatch using nondominated sorting genetic algorithm-II[J].International Journal of Electrical Power & Energy Systems, 2008, 30(2): 140-149.

[20]邓威，李欣然，李培强，等.基于互补性的间歇性分布式电源在配网中的优化配置[J].电工技术学报，2013，28(6)：216-225.

ZHENG Wei, LI Xinran, LI Peiqiang, et al.Optimal allocation of intermittent distributed generation considering complementarity in distributed network[J].Electric Power Automation Equipment, 2013, 28(6): 216-225.

[21]宋艺航，谭忠富，李欢欢，等.促进风电消纳的发电侧、储能及需求侧联合优化模型[J].电网技术，2014，38(3)：610-615.

SONG Yihang, TAN Zhongfu, LI Huanhuan, et al.An optimization model combining generation side and energy storage system with demand side to promote accommodation of wind power[J].Power System Technology, 2014, 38(3): 610-615.

刘 旭(1991)，男，硕士研究生，主要研究方向为计及需求侧响应的电力系统优化调度；

杨德友(1986)，男，博士，副教授，硕士生导师，研究方向为电力系统稳定与控制的研究；

孟 涛(1990)，男，研究生，工程师，主要研究方向为分布式电源规划、新能源并网；

张 旺(1989)，女，研究生，研究方向为基于随机响应的电力系统小干扰稳定分析；

刘 曦(1989)，女，研究生，工程师，研究方向为电力系统稳定运行与安全控制；

姜明磊(1991)，男，硕士研究生，工程师，研究方向为交流微网分层控制。

(编辑 蒋毅恒)

Day-Ahead Tow-Stage Dynamic Economic Emission Dispatching in Wind Power Integrated System Incorporating Demand Response

LIU Xu1, YANG Deyou1, MENG Tao2, ZHANG Wang1, LIU Xi3, JIANG Minglei3

(1.School of Electrical Engineering,Northeast Dianli University, Jilin 132012, Jilin Province, China; 2.Electric Power Research Institute, State Grid Jilin Electric Power Co., Ltd., Changchun 130021, China; 3.Economic Technology Institute, State Grid Jilin Electric Power Co., Ltd., Changchun 130000, China)

As an important interactive resource between generation side and demand side, demand response can effectively regulate the distribution of load demand to achieve energy-saving and emission-reduction and improve the system wind power capacity.Based on this, this paper considers the demand response in the environmental economic and proposes a day-ahead two-stage dispatching model under smart grid.The first stage is day-ahead user interaction stage, in which the next day load distribution is adjusted by time-of-use price leverage guiding the user to take rational power consumption and the optimal load curve and time-of-use price is determined by considering the load level and user satisfaction index.The second stage is day-ahead dispatching stage, in which the economic emission dispatch model is established based on chance-constrained programming for wind power randomness and this model is transformed into a deterministic model by using wind power distribution function.We propose an improved multi-objective particle swarm optimization algorithm by introducing the diversity index, random black hole theory and the multi-targeted search mechanism, and adopt technique for order preference by similarity to ideal solution(TOPSIS) method to sort the Pareto frontier individual to help the dispatcher to make scientific decision.The simulation results of the improved 10 machine system verify the validity and rationality of the model and method.

wind power; demand response; time-of-use price; customer’s satisfaction; economic emission dispatch; technique for order preference by similarity to ideal solution(TOPSIS)

国家高技术研究发展计划项目(863计划)(SS2014AA052502)；国家自然科学基金项目(51377017)；长江学者和创新团队发展计划资助项目(IRT114)

Project supported by the National High Technology Research and Development of China (863 Program) (SS2014AA052502)；Project supported by the National Natural Science Foundation of China(51377017) ；Project supported by Changjiang Scholars and Innovative Research Team in University(IRT0720)

TM 73; TM 614

A

1000-7229(2016)09-0146-09

10.3969/j.issn.1000-7229.2016.09.020

2016-05-12