主梁开闭口形式对斜拉桥动力特性的影响

于 哲

(中交第二公路勘察设计研究院有限公司， 湖北 武汉 430056)

主梁开闭口形式对斜拉桥动力特性的影响

于 哲

(中交第二公路勘察设计研究院有限公司， 湖北 武汉 430056)

斜拉桥动力特性分析是抗震和抗风稳定性分析的基础。以主跨538 m的预应力叠合梁双塔双索面半漂浮体系斜拉桥为研究对象，采用大型有限元软件ANSYS，分别对3种主梁形式(全开口π型、分离边箱半开口型、底板封闭型)建立空间有限元模型，对其进行动力特性分析并加以对比。结果表明：分离边箱半开口截面与底板封闭截面2种主梁截面形式下，斜拉桥振动特点相似，故增加底板使主梁形成封闭体系对斜拉桥振动特性影响不大；开口π型截面与后两种截面形式相比，各种振型出现的阶次不完全相同，纵飘频率、扭转频率和索塔侧向弯曲频率较小，对桥梁的地震响应和抗风稳定性不利，竖向弯曲频率和横向弯曲频率较大，对桥梁的地震响应和抗风稳定性有利。

斜拉桥； 动力特性； 主梁形式； 有限元

在大跨桥梁中，箱梁是常用横断面形式，一般为单箱单室或单箱多室。随着斜拉桥和悬索桥的出现，桥梁极限跨度被进一步提高。其跨度不断增大，对主梁的自重提出了更苛刻的要求。为减轻桥梁自重，又保证桥梁的受力性能，工程师们在长时间的工程实践中设计了多种不同的主梁截面形式。在传统箱型截面形式的基础上衍生出应用较多的全开口π型、分离边箱半开口型和底板封闭型的截面形式。开口和半开口截面形式在很大程度上减轻了主梁自重，同时降低了主梁扭转刚度，对桥梁抗风和抗震稳定性产生一定影响。文章以主跨538 m的斜拉桥为研究对象，分别设计以上3种不同主梁断面形式，分析对比其动力特性结果，得出3种方案不同的动力特性，为优化主梁断面形式提供依据。

1 工程概况

该斜拉桥主桥结构是双塔双索面半漂浮体系，全长940 m，主跨538 m，跨径布置为(220+538+182)m，在左右边跨设有辅助墩。全桥采用钢混叠合梁形式，梁高3.6 m，宽37 m，在有斜拉索处设置横隔板。索塔采用空心箱形混凝土结构，塔高(含塔冠)189 m。全桥共设68对斜拉索，拉

索采用扇形布置，横桥向索距为34.8 m，顺桥向标准索距为15 m，并对靠近边跨端头附近的尾索进行加密，尾索索距为10 m。桥型布置见图1。

图1 斜拉桥桥型布置图(单位： cm)

文章研究3种主梁截面形式对斜拉桥动力特性的影响。3种主梁截面如图2所示。

图2 3种主梁截面形式图(单位： mm)

2 研究机理

由结构动力学的基础知识，有结构体系的动力学平衡方程：

(1)

在研究桥梁结构自振频率时，外荷载置为零，同时忽略阻尼的影响，故可得到研究桥梁自振频率的基础方程：

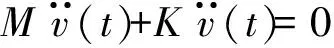
(2)

其特征方程为：

(K-ω2M)u=0

(3)

其中，ω为桥梁结构自由振动频率；u为振动体系的相应阵型。

3 计算模型

桥面梁单元和索塔单元采用BEAM4和BEAM44模拟，拉索单元用LINK8模拟，二期恒载(桥面铺装等)通过质量单元MASS21模拟。对于纵向半漂浮体系斜拉桥，认为在塔梁连接处，主梁节点和塔节点竖向、横向和扭转位移一致，因此在建模时，对于全桥边界及约束条件，此处节点的3

个位移(竖向、横向、扭转)进行耦合处理，同理，梁与边墩和辅助墩的连接处也进行耦合处理，同时，对桥塔和下部结构的底部进行固结处理。全桥有限元模型如图3所示。

图3 全桥有限元模型

4 结果分析

模态分析主要有子空间迭代法、多重Ritz向量法和Lanczos 3种方法。在子空间迭代技术中，采用完整的刚度矩阵和质量矩阵在子空间投影，精度很高，这种迭代算法对计算机内存要求也较低。因此，文章采用有限元分析程序ANSYS中的子空间迭代法，建立3种主梁截面形式下斜拉桥整体模型并进行动力特性计算分析，提取和扩展频率数量为30。现将能比较准确反映其振动特点的前10阶自振频率和振型特点列于表1中。

表1 3种截面形式自振频率和振型特点对比阶次开口π型截面分离边箱半开口截面底板封闭截面自振频率/Hz振型特点自振频率/Hz振型特点自振频率/Hz振型特点100732纵飘00972纵飘00971纵飘2032211阶正对称竖弯02989横弯02958横弯303254桥塔同向侧弯030111阶正对称竖弯030311阶正对称竖弯403350桥塔异向侧弯03571桥塔异向侧弯03569桥塔异向侧弯5040721阶反对称竖弯03678桥塔同向侧弯03672桥塔同向侧弯604129横弯039411阶反对称竖弯040641阶反对称竖弯7050921阶正对称扭转052621阶正对称扭转052371阶正对称扭转8054491阶反对称扭转054462阶正对称竖弯056862阶正对称竖弯9057602阶反对称扭转060711阶反对称扭转060431阶反对称扭转10059662阶正对称竖弯064922阶反对称扭转064582阶反对称扭转

其中，有代表性的主要振型图如图4、图5所示(由于底板封闭截面的振型与分离边箱半开口截面相近，不再列出)。

由表1及图4和图5的结果对比可知，3种不同主梁截面形式下的斜拉桥动力特性有以下几点异同：

1) 虽然主梁截面形式不同，但斜拉桥总体结构体系是相同的，即双塔双索面半漂浮体系。故3种截面形式下，第1阶振型均为纵飘，且1阶正对称竖弯、1阶反对称竖弯、1阶正对称扭转、1阶反对称扭转以及主梁横弯均出现在前10阶振型中，是主要振型，这是符合该桥梁体系振动特点的。

a) 第1阶振型图

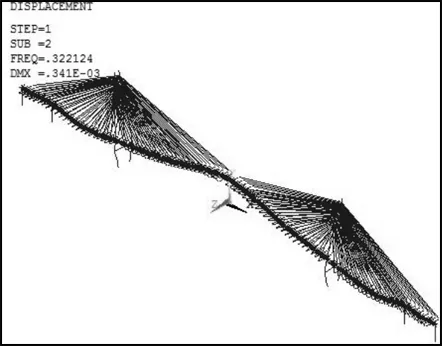
(纵飘，f=0.073 2) b) 第2阶振型图

(1阶正对称竖弯，f=0.322 1)

c) 第6阶振型图

(横弯，f=0.412 9) d) 第7阶振型图

(1阶正对称扭转，f=0.509 2)

图4 开口π型截面主要振型

a) 第1阶振型图

(纵飘，f=0.097 2) b) 第2阶振型图

(横弯，f=0.298 9)

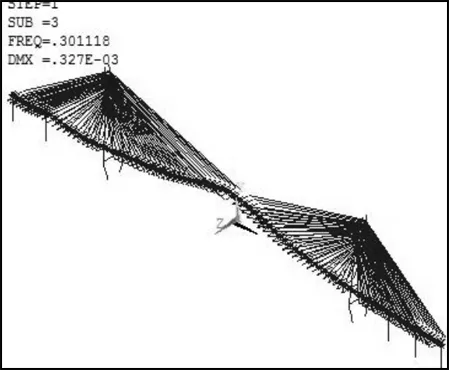
c) 第3阶振型图

(1阶正对称竖弯，f=0.301 1) d) 第7阶振型图

(1阶正对称扭转，f=0.526 2)

图5 分离边箱半开口截面主要振型

2) 分离边箱半开口截面与底板封闭截面2种主梁截面形式下，斜拉桥振动特点相似，其振型特点及出现的阶次相同，相应自振频率数值相差1%左右(大部分不足1%)，由此可见，增加底板使主梁形成封闭体系对斜拉桥振动特性影响不大；开口π型截面与后2种截面形式相比，各种振型出现的阶次不完全相同，纵飘频率、扭转频率和索塔侧向弯曲频率较小，竖向弯曲频率和横向弯曲频率较大。由于在抗风动力分析时，扭弯频率比对颤振起至关重要的影响，因此π型截面较小的扭转频率不利于桥梁抗风稳定，但其竖向弯曲频率和横向弯曲频率较大，有利于桥梁的地震响应和抗风稳定性。

5 结论

该文利用大型有限元分析软件ANSYS对某斜拉桥不同主梁截面形式(全开口π型、分离边箱半开口型、底板封闭型)进行建模分析，提取其自振频率和振型，并对得到的结果加以对比分析，得出以下结论：

1) 3种方案虽然主梁截面形式不同，但都具有双塔双索面半漂浮体系斜拉桥的振动特性。虽然各振型出现的阶次不完全相同，但纵飘、横弯、竖弯、扭转及桥塔横弯等振型均是其主要振动形式。

2) 将分离边箱半开口截面底板封闭形成封闭截面，不能有效提高桥梁动力稳定性，但却增加了桥梁自重，由此会增大主梁挠度，同时增加工程造价。因此，除非有特殊需求，建议工程中不采取第3种底板封闭的截面形式。

3) 开口π型截面与分离边箱半开口截面相比，较小的扭转频率对桥梁动力稳定性是不利的，但较大的竖弯频率和横弯频率却是有利的。因此，在桥梁设计和工程实践中，建议根据具体的工程需要，在二者中选择合适的截面形式。

[1] 李加武，黄森华，王新.开口断面斜拉桥主梁动力特性的有限元简化计算[J].建筑科学与工程学报，2013(4)：59-64.

[2] 尹晓明，朱益民，赵研峰.斜拉桥动力模型分析[J].铁道标准设计，2003(10)：38-39.

[3] 王伟，黄永福，周聪，等.辅助墩对无上横梁双直立塔柱斜拉桥的影响[J].中外公路，2012(5)：119-123.

[4] 曹少辉，谢勇.砼双塔斜拉桥的动力特性研究[J].公路与汽运，2014(2)：159-161.

[5] 曹海滨.大跨度混合梁斜拉桥抗风性能分析[J].铁道标准设计，2005(10)：36-38.

[6] 陈健蕾，冯清海.大跨度斜拉桥不同模拟方法对结构特性及响应的影响[J].公路，2010(5)：43-45.

[7] 王建新，马存明，高伟，等.斜拉桥单、双主梁建模动力特性比较[J].四川建筑科学研究，2013(6)：165-168.

1008-844X(2016)04-0076-03

U 448.27

A