风电机组齿轮箱行星轮裂纹故障仿真分析

邓小文，冯永新，钟龙

(1.广东电网有限责任公司电力科学研究院，广东 广州 510080；2.华中科技大学 能源与动力工程学院,湖北 武汉 430074)

风电机组齿轮箱行星轮裂纹故障仿真分析

邓小文1，冯永新1，钟龙2

(1.广东电网有限责任公司电力科学研究院，广东 广州 510080；2.华中科技大学 能源与动力工程学院,湖北 武汉 430074)

受强交变载荷的影响，非直驱风力机齿轮箱极易发生故障，为此研究风电机组齿轮裂纹故障诊断新方法。理论分析了风电机组齿轮裂纹故障振动信号特征，建立了行星轮裂纹故障仿真研究模型，通过改变啮合刚度参数模拟齿轮裂纹故障。研究结果表明，当行星轮存在裂纹故障时，故障齿的啮合会对齿轮的振动产生调峰作用，振动信号具有啮频及谐波两侧会出现行星轮转频、故障特征频率及两者组合的调制边频带的特征。

风力发电；齿轮箱；故障诊断；仿真；行星轮；振动信号分析

风力发电作为清洁可再生能源，近年来在我国得到了飞速发展，截至2015年底，并网风机装机容量达128 GW[1-3]。但是，风能的间歇性、随机性以及风机的重载低速等特性，影响了风力发电机组的安全稳定运行。风力发电机组齿轮箱故障是影响风电机组稳定运行的典型机械故障之一，但目前对齿轮箱的故障建模以及故障信号产生机理的分析还较为欠缺[4-7]。本文分析了齿轮裂纹故障信号的产生机理，建立了基于MATLAB/Simulink平台的齿轮箱动力学模型，通过改变啮合刚度参数模拟齿轮箱行星轮裂纹故障[8-11]，最后联合风电机组整机模型[12]进行了仿真分析，分析结果为风电机组齿轮箱基于模型的故障诊断研究提供技术参考。

1 齿轮裂纹故障机理分析

本文以行星轮裂纹故障作为研究对象。除了齿轮局部故障的调幅调频效应外，行星轮系的裂纹故障还有由于行星轮随行星架旋转产生的调幅作用[11]。

1.1 行星轮的故障频率

对于存在裂纹故障的齿轮，啮合时由于啮合刚度的突然降低将会在故障处产生冲击，随着齿轮的旋转，这种冲击将会按照一定的规律周期性地出现，这个周期所对应的频率即为齿轮局部故障频率。对于定轴轮系，齿轮局部故障产生的周期性冲击的频率为齿轮的转频；而对于行星轮系，局部故障对应的频率为行星轮系的啮频除以行星轮的齿数，啮频定义为其在动坐标系Oxy中相对转频与齿数之积。

故行星轮与太阳轮的啮合频率

(1)

行星轮与内齿圈的啮合频率

(2)

因为行星轮同时与两者啮合，所以行星轮与两者的啮合频率相等，即

(3)

行星轮在其一个旋转周期内会分别与太阳轮和内齿圈发生一次故障齿的啮合，所以行星轮相对于太阳轮和内齿圈的故障特征频率

(4)

以上各式中：Zp、Zr和Zs分别为行星轮、内齿圈和太阳轮齿数；fs、fc分别为太阳轮和行星架的转频；fm为行星轮啮合频率。

若忽略行星轮故障轮齿分别与太阳轮和内齿圈啮合时的冲击差异，则在行星轮自转的1个周期内有2次相同的冲击，此时行星轮故障特征频率为2fp。

1.2 行星轮裂纹振动信号分析

啮合刚度作为齿轮传动系统的内部激励，会引起齿轮周期性振动，在振动信号频域上可表示为啮合频率及其各次谐波[9]

(5)

式中：x(t)是与时间t相关的振动信号幅值；Ak为谐波振幅；φk为谐波相位。

齿轮局部裂纹故障导致齿轮振动幅值、频率的变化，通常会出现以啮频及其谐波为载波的调制现象，通常同时出现幅度调制和频率调制。

为简化计算，考虑单频率调制，只关注级数中的基频成分，即啮频与故障特征频率，齿轮故障的振动信号响应可简化为

(6)

式中：[1+Bcos(2πfgt+γ)]表示故障齿轮调幅；Csin(2πfgt+ψ)表示故障齿轮调频；A与φ分别为啮合频率的振幅和相位；B与C分别为幅值调制和频率调制的指数；fg为局部故障频率；γ和ψ分别为调制函数的初始相位。

由变量为x和y的三角函数恒等式

和欧拉公式

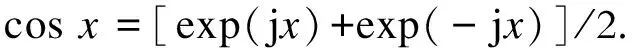
以及恒等式

式(6)可推导为

(7)

式中Jn(x)为n阶(n为整数)第一类柱贝塞尔(Bessel)函数。

对H(x,y)进行仅考虑正频率的傅里叶变换，得

(8)

式中δ为狄拉克分布函数。则式(7)经简化及考虑正频率部分的傅里叶变换，可得与频率f相关的振动信号幅值

(9)

由式(9)可知，实际齿轮系统中的调幅调频共存时，边频带出现在fm±nfg(n为整数)处，即以fm为中心、fg为间隔的均匀频带。

1.3 行星架旋转调幅效应

行星轮公转的“通过效应”会使行星架的转动对太阳轮与行星轮局部故障振动信号产生额外调幅作用。则齿轮振动信号响应可表示为

(10)

式中[1-cos(2πfct)]表示行星架旋转调幅。x(t)经简化及傅里叶变换可得

(11)

由式(11)可知：当太阳轮或者行星轮发生故障时，其振动频谱中，啮频fm及各次谐波两侧边频成分中将出现故障特征频率、行星架转频及两者组合的调制边频带：fm±nfg，fm±mfc和fm±mfc±nfg(m为整数)。

2 行星轮齿根裂纹故障建模

2.1 齿轮箱模型的建立

以风电机组一级行星轮和两级平行轴直齿轮系统为研究对象，建立齿轮箱扭转-横向振动的运动微分方程数学模型[11]

(12)

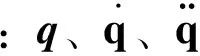
(13)

2.2 齿轮箱模型仿真分析

取齿轮传动系统的传动比为94.527，其他基本参数见表1[11]。

表1 行星轮系基本参数

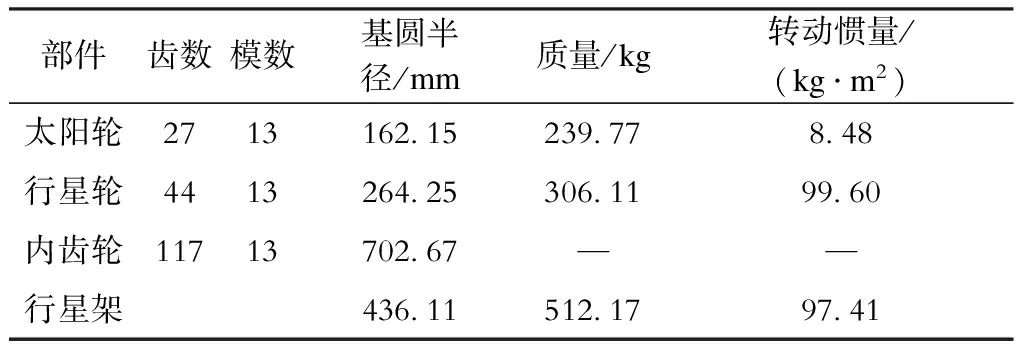
部件齿数模数基圆半径/mm质量/kg转动惯量/(kg·m2)太阳轮27131621523977848行星轮441326425306119960内齿轮1171370267——行星架43611512179741

借助MATLAB/Simulink建立齿轮箱框图模型，并结合风电机组整机模型(图1)进行联合仿真。风电机组为定速型，电机为鼠笼异步发电机，鉴于模型的刚性，求解器选用ode23t，仿真时间为30 s。正常状态下，模型所用风速以及叶轮输出转矩如图2所示，叶轮输出转矩经过初始短暂的波动后，变化趋势与风速基本保一致。

1/s—MATLAB Simulink中积分模块；S—MATLAB Simulink中示波器模块(scope)；nt—叶轮转速；s1—叶轮旋转角位移；v—塔架顶端前后方向振动速度；θ—塔架顶端前后方向转角；ω1—塔架顶端前后方向旋转角速度；vs—塔架顶端左右方向的振动速度；θs—塔架顶端左右方向转角；ωs—塔架顶端左右方向的旋转角速度；T—叶轮输出扭矩；Tm—电磁转矩；M—弯矩；Tg—不平衡转矩；ma—质量不平衡量；φp—不平衡质量块的相位。图1 风电机组整机模型

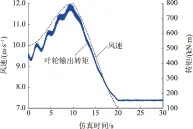
图2 风速以及叶轮输出转矩

齿轮箱各部件转速变化如图3所示，各对相互啮合齿轮转速比基本符合其传动比关系。叶轮(行星架)、行星轮、太阳轮所在轴的转频分别为fc=0.325 Hz、fr=0.52 Hz、fs=1.7 Hz，中速级小齿轮和高速级小齿轮所在轴的转频分别为7.66 Hz和30.12 Hz。对于行星轮系，由转频计算出的传动比为92.677，与系统传动比有微小差异，误差为1.96%。由图3分析可知该误差是由齿轮箱各部件转速波动导致的。但该误差在允许范围内，可以认为各部件转速完全符合绝对转速与行星架转速及各自齿数的传动比规律，表明建模正确。

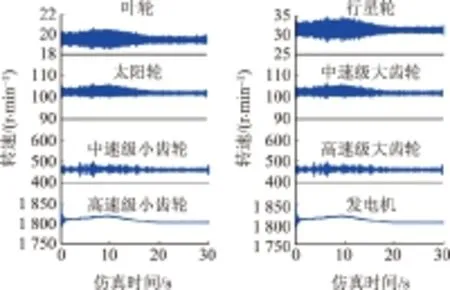
图3 齿轮箱各部件绝对转速

将太阳轮转频fs和行星架转频fc代入到式(1)至(4)，结合表1中的齿轮参数，可计算出行星轮啮合频率为fm=37.9 Hz，故障特征频率为fp=0.86 Hz。

2.3 行星轮裂纹故障模拟

齿轮的单对轮齿综合啮合刚度(包括弯曲、剪切以及轴向压缩刚度)取决于轮齿的几何参数。对于齿轮的裂纹故障，也可以归结为齿轮几何形状的改变，从而导致轮齿啮合刚度的变化。

由材料力学的裂纹梁理论可知，与正常的轮齿相比，有裂纹故障的轮齿参与啮合时，啮合刚度会减少。通过计算可知，当发生裂纹故障达到一定程度时，啮合刚度减少幅度可达50%，啮合刚度变化如图4所示。本文采用减少轮齿啮合刚度来模拟实现齿轮故障。

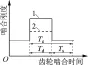
Te—刚度变化的周期；Td—双齿对啮合阶段；Ts—单齿对啮合阶段；1—正常情况时的刚度；2—有裂纹故障时的刚度。图4 轮齿啮合刚度变化模型

3 行星轮裂纹故障仿真分析

图5给出了行星轮正常状态和故障状态的x方向时域振动波形。易知，故障状态下的振动波形存在明显的周期性冲击，如图5(b)所示，图中用实心圆点标注了幅值略高的冲击，而另外一些幅值较低的冲击则用空心圆点标识。这2组点的间隔均约为1.16 s，它正好对应行星轮的局部故障特征频率0.86 Hz。由于行星轮与太阳轮的啮合刚度较之与内齿圈之间的啮合刚度要低，同样故障程度下，行星轮故障齿与太阳轮啮合时产生的冲击要略高。因此，这2组一高一低幅值的冲击应为行星轮故障齿分别与太阳轮和内齿圈啮合时产生。

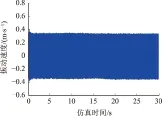
(a)正常状态

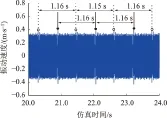
(b)故障状态图5 行星轮x方向振动速度

对比分析图6、图7所示的振动速度频谱可知，故障状态行星轮x方向的啮频(37.9 Hz)及其各次谐波之间有调制现象。

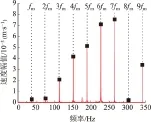
图6 正常状态行星轮x方向振动速度频谱

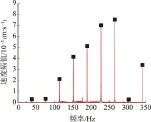
图7 故障状态行星轮x方向振动速度频谱

图8展示了行星轮系啮频五倍频(37.9 Hz×5≈189.7Hz)的下侧和上侧边频带。在图中除了用实心点和虚线标记的行星轮故障特征频率的边频带5fm±nfp，还有空心点和实线标记的行星架旋转调制边频带5fm±nfc，详见表2和表3；以及用数字(下边带)和字母(上边带)标注的空心点处的行星轮故障特征频率和行星架转频调制的5fm±nfp±mfc处的边频带，详见表4和表5。这些频率等式的误差均低于0.06，与理论分析结果一致。

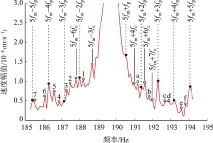
图8 5倍啮频故障状态行星轮x方向振动速度频谱

表2 故障行星轮五倍啮频下边带5fm-nfp和5fm-mfc处频率及速度幅值

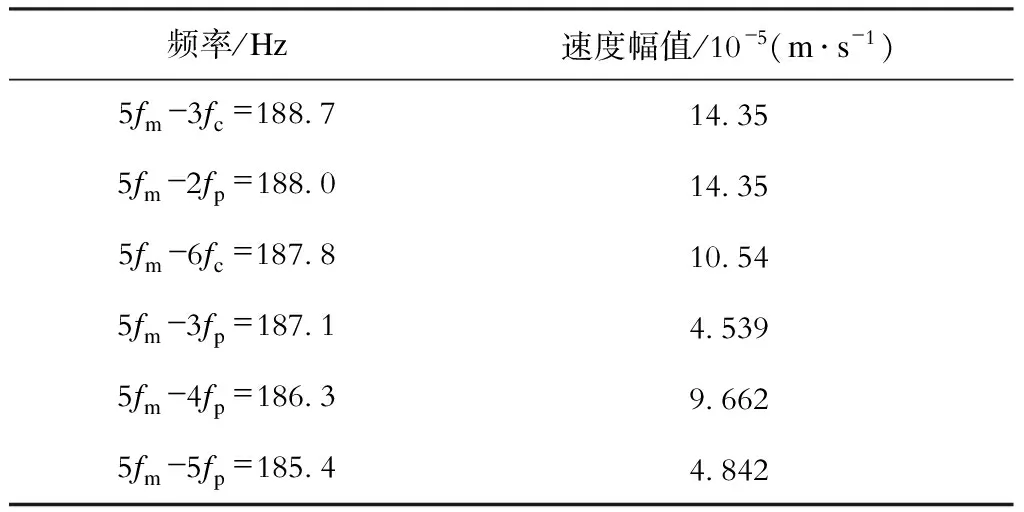
频率/Hz速度幅值/10-5(m·s-1)5fm-3fc=188714355fm-2fp=188014355fm-6fc=187810545fm-3fp=187145395fm-4fp=186396625fm-5fp=18544842

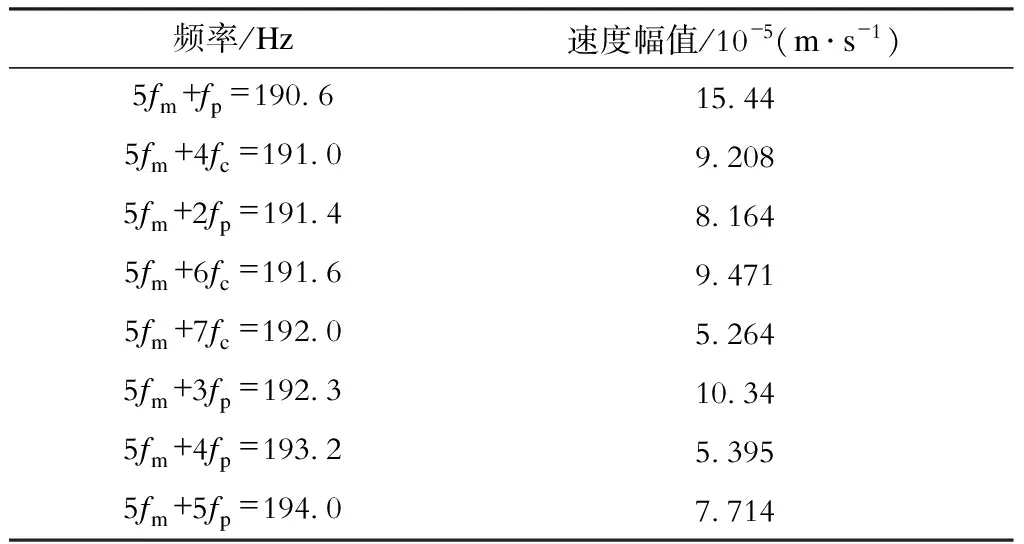
表3 故障行星轮五倍啮频上边带5fm+nfp和5fm+mfc

表4 故障行星轮五倍啮频下边带5fm-nfp-mfc处频率及速度幅值

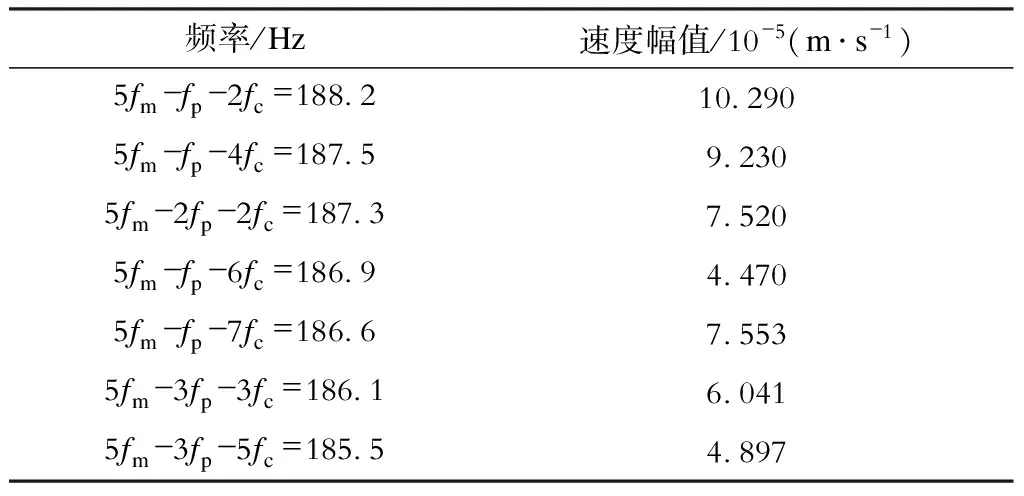
频率/Hz速度幅值/10-5(m·s-1)5fm-fp-2fc=1882102905fm-fp-4fc=187592305fm-2fp-2fc=187375205fm-fp-6fc=186944705fm-fp-7fc=186675535fm-3fp-3fc=186160415fm-3fp-5fc=18554897

表5 故障行星轮五倍啮频上边带5fm+nfp+mfc处频率及速度幅值

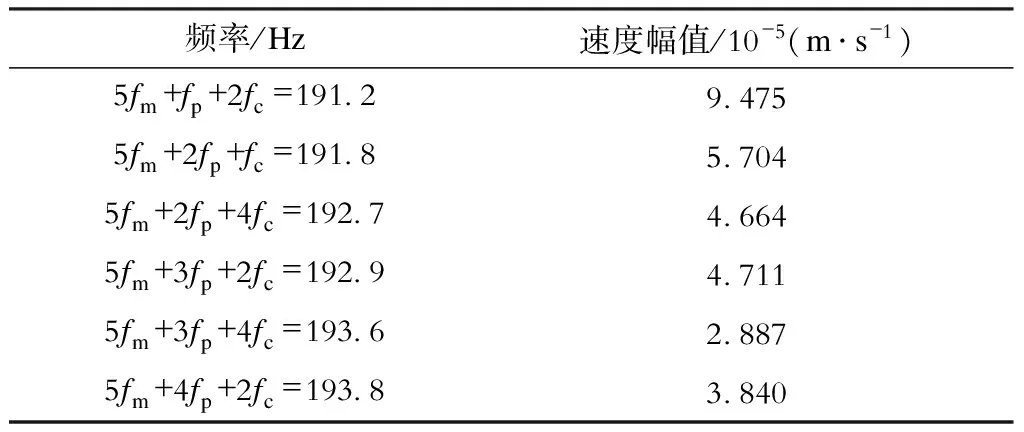
频率/Hz速度幅值/10-5(m·s-1)5fm+fp+2fc=191294755fm+2fp+fc=191857045fm+2fp+4fc=192746645fm+3fp+2fc=192947115fm+3fp+4fc=193628875fm+4fp+2fc=19383840

如图8所示的下边带中，当n=1时，5fm-fp所对应的峰值较其他峰值并不明显；而上边带中，5fm+fp则难以分辨。这是由于5倍啮频比行星轮故障频率或者行星架转频要高出1～2个数量级，靠近5倍啮频的一些调制频率被“湮没”在5倍频峰值中。同理，对于5fm+mfc边频成分，由于行星架转频(fc=0.325 Hz)非常小，且因为由微弱局部故障造成行星轮载荷不均而带来的行星架旋转调幅效应也非常微弱，在图8中只能分辨出fm-3fc、fm±6fc、fm+4fc、fm+7fc等几个边频成分。

由于行星轮故障频率(fp=0.86 Hz)较小，在图7和图8的频谱中较难分辨出来，而图9所示故障状态行星轮x方向振动速度倒谱中间隔为1.16 s的峰值和图5所示故障行星轮时域振动波形中间隔同为1.16 s的冲击相结合，能够很容易的观察到行星轮故障频率。再次验证倒谱在分离周期性信号中的优势所在；另外，倒谱分析还能够削弱由于传感器测点和不同振动传输路径对信号的调幅作用的影响。

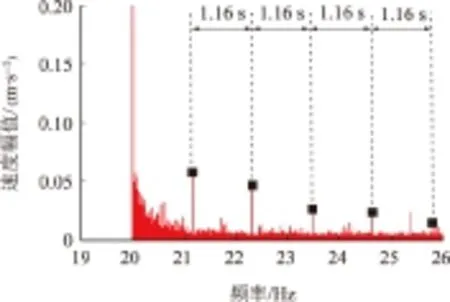
图9 故障状态行星轮x方向振动速度倒谱

4 结束语

通过建立齿轮箱模型，结合风力机整体模型仿真，模拟分析了齿轮裂纹故障的振动信号成分，发现对于行星轮裂纹故障，由于故障齿在啮合过程中会使行星轮的载荷分配不均，会对振动产生调幅作用，因此啮频及其谐波两侧会出现行星轮转频、故障特征频率及两者组合的调制边频带，与理论分析结果一致，为风电机组齿轮箱故障诊断提供了一种行之有效的方法。

[1] 田德，马晓慧.国内外大型风电机组关键技术发展趋势(一)[J]. 风能，2016(1)：32-36.

TIAN De，MA Xiaohui. The Development Trend of Key Technologies of Large-scale Wind Turbines at Home and Abroad (1)[J]. Wind Energy，2016(1)：32-36.

[2] 田德，马晓慧.国内外大型风电机组关键技术发展趋势(二)[J]. 风能，2016(3)：28-31.

TIAN De，MA Xiaohui. The Development Trend of Key Technologies of Large-scale Wind Turbines at Home and Abroad (2)[J]. Wind Energy，2016(3)：28-31.

[3] GWEC.Global Wind Report Annual Market Update 2014[R]. Istanbul：GWEC，2015.

[4] 张延超. 故障齿轮传动系统动力特性分析与寿命研究[D]. 西安：西北工业大学，2006.

[5] 王晨清，宋国兵，迟永宁，等.风电系统故障特征分析[J]. 电力系统自动化，2015，39(21)：52-58.

WANG Chenqing，SONG Guobing，CHI Yongning，et al. Fault Characteristics Analysis of Wind Power System[J]. Automation of Electric Power Systems，2015，39(21)：52-58.

[6] 辛卫东.风电机组传动链振动分析与故障特征提取方法研究[D]. 北京：华北电力大学，2013.

[7] 丁显，易莉，柳亦兵，等.风电机组齿轮箱非平稳振动信号微弱故障特征提取[J]. 可再生能源，2014，32(5)：619-623.

DING Xian，YI Li，LIU Yibing，et al. Weak Fault Characteristics Extraction of Non-stationary Vibration Signal for Wind Turbine Gearbox[J]. Renewable Energy Resources，2014，32(5)：619-623.

[8] 张青锋，唐力伟，郑海起，等. 轮齿疲劳裂纹非线性动力学模型的参数确定及仿真[J]. 振动、测试与诊断，2011，31(1)：94-97.

ZHANG Qingfeng，TANG Liwei，ZHENG Haiqi，et al. Parameters Determination and Simulation Analysis of Nonlinear Dynamic Model of Gear Tooth Fatigue Crack[J]. Journal of Vibration,Measurement & Diagnosis，2011，31(1)：94-97.

[9] 丁康，李巍华，朱小勇. 齿轮及齿轮箱故障诊断实用技术[M]. 北京：机械工业出版社，2005.

[10] ZHONG Long，ZHANG Lei，YANG Tao，et al. Research on Fault Modeling and Simulation of the Drive Chain of Wind Turbine[C]//International Conference on Applied Mechanicsand Mechanical Engineering.London：Information Engineering Research Institute，2015：5-11.

[11] 李润方，王建军. 齿轮系统动力学:振动、冲击、噪声[M]. 北京：科学出版社，1997.

[12] 任永. 风力机轮不平衡故障建模与仿真研究[D]. 武汉：华中科技大学，2012.

(编辑 霍鹏)

Simulation Analysis on Crack Fault of Planetary Wheel of Wind Turbine Gearbox

DENG Xiaowen1, FENG Yongxin1, ZHONG Long2

(1. Electric Power Research Institute of Guangdong Power Grid Co., Ltd., Guangzhou, Guangdong 510080, China; 2. School of Energy and Power Engineering, Huazhong University of Science and Technology, Wuhan, Hubei 410116, China)

Affected by strong alternating load, the gearbox of non-direct-driven wind turbine is easy to break down, therefore, this paper aims to study a new method for diagnosis on crack fault of wheel gear of the wind turbine. It theoretically analyzes characteristics of crack fault vibration signals and establishes a simulation and research model for crack fault of the planetary wheel so as to simulate crack fault of the wheel gear by changing meshing stiffness parameters. Research results indicate that when there is crack fault in the planetary gear, meshing of the faulted gear will have peak regulating effect on vibration of the wheel gear. In addition, vibration signals have the characteristic that rotating frequency of the planetary wheel, faulted characteristic frequency and combined regulating sideband are all occurred at both sides of meshing frequency and harmonic of mesh frequency.

wind power generation; gearbox; fault diagnosis; simulation; planetary wheel; vibration signal analysis

2016-08-02

2016-10-13

国家科技支撑计划资助项目(2015BAA06B02)

10.3969/j.issn.1007-290X.2016.12.005

TK83

A

1007-290X(2016)12-0021-06

邓小文(1974)，男，湖南祁阳人。教授级高级工程师，工学博士，从事风力发电技术研究及振动故障诊断处理等工作。

冯永新(1968)，男，广西柳州人。教授级高级工程师，工学博士，从事动力机械及工程相关研究工作。

钟龙(1990)，男，湖南汨罗人。助理工程师，工学硕士，主要从事风电机组建模以及故障仿真、核电机组冷端优化工作。