基于改进Kruskal算法的变电站机器人路径规划
2017-01-10徐平刘悦
徐平, 刘悦
(1. 广东电网有限责任公司江门供电局,广东 江门 529000;2. 东北电力大学 自动化工程学院,吉林 吉林 132012)
基于改进Kruskal算法的变电站机器人路径规划
徐平1, 刘悦2
(1. 广东电网有限责任公司江门供电局,广东 江门 529000;2. 东北电力大学 自动化工程学院,吉林 吉林 132012)
鉴于目前中国变电站智能巡检机器人多采用磁感应线配合射频识别技术的导航方式实现定点巡视,对机器人巡视点的路径规划问题进行研究。首先,考虑到精确算法的复杂性,用近似算法对巡视路径进行规划,以贪心算法和局部搜索思想为主,结合启发式算法对求最小支撑树的Kruskal算法进行改进;然后,用MATLAB软件编程求出机器人的最短巡视路径;最后,用遗传算法求出最短路径,并将遗传算法和改进的Kruskal算法下的最短巡视路径进行比较。比较结果表明:改进的Kruskal算法优势明显,且适用于小规模变电站巡视路径规划。
变电站智能巡检;改进的Kruskal算法;最短巡视路径
变电站智能巡检机器人能否安全自主运行,可靠的导航系统尤为重要。目前,导航方式主要有磁导航、全球定位系统(global position system,GPS)导航、激光导航、惯性导航和构建地图导航等[1-2],在中国用得最多的是磁导航方式,即在场地铺设或者埋藏磁性感应线配合射频识别(radio frequency identification,RFID)技术进行定位导航。机器人按照一定的路线行走并实现定点巡视,因此机器人的路径规划问题成为研究重点之一。
机器人从充电室出发,巡视一周,最后返回充电室,形成一条回路,机器人的路径规划就是求路程的最小值。这种问题类似于求最短路中的旅行商问题(tranveling salesman problem,TSP)[3],即某人从任一城市出发,途径n个城市,并且每个城市只经过1次,旅行后回到出发城市,使得行走路程(或费用)最小。针对TSP有精确算法、近似算法和智能算法,精确算法有运筹学中的线性规划法、分支定界法、动态规划法等,这些方法虽然能够求出最优解,但是计算量巨大;随着智能算法的兴起,进化算法[4]、遗传算法[5]、混合遗传算法、模拟退火算法[6]、退火遗传算法、蚁群算法[7]、神经网络算法[8]、禁忌搜索等智能算法也被用到TSP的求解中,且在城市较多时取得了较好的结果。
本文根据变电站的实际情况,以近似算法中贪心算法和局部搜索的思想为主,考虑改进Kruskal算法,通过编写MATLAB程序[9]实现路径规划。首先用原始的Kruskal算法根据权值矩阵求出路径的最小支撑树,然后对Kruskal算法进行改进,从各个巡视点出发,通过最小完美匹配等方法实现路径的规划;最后给出算例,对某变电站进行巡视,分别用改进的Kruskal算法和遗传算法[10]求出最短路径,并对两种算法得到的结果进行分析对比。
1 变电站智能机器人路径规划建模
1.1 建模原则
变电站智能巡检机器人路径规划建模主要遵循以下原则:
a)选择充电室巡视点作为出发点和终点;
b)每个巡视点只经过一次;
c)目标是使巡视路径的路程最小。
1.2 目标函数
目标函数为
(1)
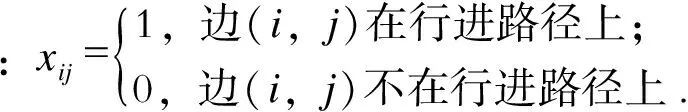
式中dij为第i个巡视点与第j个巡视点的距离。
1.3 约束条件
1.3.1 约束条件1
约束条件1是保证巡检机器人每个巡视点只巡视一次。
式中n为巡视点的数量。
1.3.2 约束条件2
约束条件2是保证机器人在行进的过程中,直到返回充电室不形成环路径。
式中S为入选进规划路径的边的集合。
2 采用Kruskal算法求最小支撑树
2.1 Kruskal算法的基本思想
Kruskal算法是一种求赋权完全图的最小支撑树算法,其应用的贪婪原则是:首先将所有点与点之间的权值排序,选择最小的权所在的边作为第一条边,之后从剩下的边中选择一条边加入到已有边中,并且保证所选的边与已有的边不构成环路,因而生成一棵最小支撑树。
2.2 Kruskal基本算法

a)对集合E中各边的权由小到大排序,即ω1≤ω2≤…≤ωm且ω1=ω(e1),其中e1为任选的第一条边;
b)令ω=0,已选边集T=∅,边的循环变量k=1,边的计数变量t=0;
c)若t=n-1,则转步骤f,否则转步骤d;
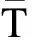
e)T=T+{ek}(ek为新选入规划路径的第k条边),ω=ω+1,k=k+1,t=t+1,转步骤c;
f)输出T和ω,结束。
3 采用改进的Kruskal算法求最短巡视路径
3.1 改进的Kruskal算法的基本思想
根据原始的Kruskal算法得出最小支撑树,其目标是得到一条巡视回路,因此从点的度考虑,每个点的度都应为2。在此时得到的结果中,点的类型可以分为3类:度大于2的点、度等于2的点、度等于1的点。再通过删除大边、找最小完美匹配等方法使得所有点的度都为2,以启发式思想找到最短路径。
3.2 改进的Kruskal基本算法
设mD为第i个顶点Vi的度。改进的Kruskal基本算法的步骤为:
a)根据权集,通过Kruskal算法求出最小支撑树;
b)若mD>2,则对其连接边由小到大排序,删除最大边;
c)若mD=0,根据贪心算法思想,则联结各点,若顶点数为1则联结其最近的mD=1的点;
d)对于mD=1的点,求最小完美匹配M;
e)将M按照从小到大的顺序加到已有支撑树中,若不产生圈则加入,否则不加入,若结果中没有链则结束,否则转步骤d。
4 算例分析
4.1 算例
以某变电站(如图1所示)为例,变电站共有18个巡视点,要求智能巡检机器人从充电室出发,将各个巡视点巡视一周后回到充电室,规划最短巡视路径。运用改进的Kruskal算法,编写MATLAB程序,求解最短路径。另外,作为方法比较,用遗传算法通过MATLAB软件编程求最短路径。为便于路径的规划,建立以充电室为原点的平面直角坐标系,将18个巡视点按照坐标的形式表示出来,如图2所示。综合考虑变电站现有磁性感应线的铺设现状,在路径规划过程中作出如下约束:各个巡视点之间的路程以实际巡检机器人在磁感应线上的路径为准,即各个巡视点距离已知;巡检原则为只对目的巡视点进行定点巡视,即保证每个巡视点只巡视一次。

图1 某变电站巡视点分布
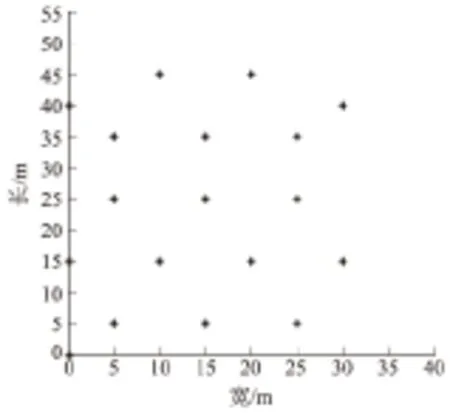
图2 某变电站巡视点散点图
4.2 改进的Kruskal算法下的最短路径规划
通过Kruskal算法得到最小支撑树(如图3所示),继而通过改进的Kruskal算法得到最短路径(如图4所示,路径连线表示巡视点到下一巡视点,下同)。

图3 最小支撑树

图4 改进Kruskal算法下的最短路径
4.3 遗传算法下的最短路径规划
设定迭代次数为50,适应值归一化淘汰加速指数为2,交叉概率为0.4,变异概率为0.2,通过编写MATLAB程序求出此变电站巡视点的最短路径,结果如图5所示。
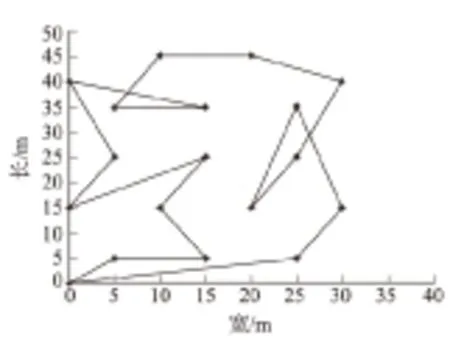
图5 遗传算法下的最短巡视路径
4.4 结果分析
对改进的Kruskal算法和遗传算法得到的最短路径进行对比,见表1。
表1 2种算法求最短路径结果比较
由表1可看到:在此变电站应用背景下,本文算法优势较为明显。
5 结论
本文针对目前我国变电站智能巡检机器人大多采用磁导航定点巡视的现状,对巡视的路径进行规划。首先用Kruskal算法求出各巡视点的最小支撑树;然后从度的角度出发,对Kruskal算法进行改进,运用启发式思想得到改进Kruskal算法下的最短路径。为便于验证此算法是否更优,用遗传算法通过MATLAB编程求出最短路径,对遗传算法和本文算法下的最短路径进行比较,结果说明本文算法优势明显。此方法可配合小规模变电站的自主导航技术,通过预先寻找巡视点路径,达到了巡视路径不经任何电力设备的目的,实现了变电站智能巡检机器人路径的合理规划。
[1] 肖鹏,栾贻青,郭锐,等.变电站智能巡检机器人激光导航系统研究[J]. 自动化与仪表,2012,(5):5-9.
XIAO Peng,LUAN Yiqing,GUO Rui,et al. Substation Inspection Robot Intelligent Laser Navigation System Research[J]. Automation and Instrument,2012(5):5-9.
[2] 李红梅,王滨海,廖文龙,等.基于地图匹配的变电站巡检机器人激光导航系统设计[J]. 制造业自动化,2014,36(1):52-56.
LI Hongmei,WANG Binhai,LIAO Wenlong,et al. Substation Inspection Robot Based on Map Matching Laser Navigation System Design[J]. Journal of Manufacturing Automation,2014,36(1):52-56.
[3] LAWLER E L, LENSTRA J K. The Traveling Salesman Problem[M]. Chichete:Wiley,1995.
[4] FOGEL D B. Applying Evolutionary Programming to Selected Taveling Salesman Problems[J]. Cybernetics and System,2011(1):24-27.
[5] 覃俊,蓝雯飞,兰华荣.用遗传算法求解旅行商问题[J]. 中南民族学院学报(自然科学版),2011,19(1):41-42.
QIN Jun,LAN Wenfei,LAN Huarong. Using Genetic Algorithm to Solve Traveling Salesman Problem[J]. Journal of Zhongnan Institute for Nationalities(Natural Sciences),2011,19(1):41-42.
[6] 高尚.求解旅行商问题的模拟退火算法[J]. 华东船舶学院学报,2013,17(3):13-16.
GAO Shang. Simulated Annealing Agorithm to Solve Traveling Salesman Problem[J]. Journal of East China Institute of the Ship,2013,17(3):13-16.
[7] 赵娟平,高宪文,符秀辉.改进蚁群优化算法求解移动机器人路径规划问题[J]. 南京理工大学学报,2011,35(5):637-641.
ZHAO Juanping,GAO Xianwen,FU Xiuhui. Ant Colony Optimization Algorithm for Solving the Mobile Robot Path Planning Problem[J]. Journal of Nanjing University of Science and Technology,2011,35(5):637-641.
[8] TEOH E J, TAN K C, TANG H J, et al. An Asynchronous Recurrent Linear Threshold Network Approach to Solving the Traveling Salesman Problem[J]. Neurocomputing,2008,71(79):1359-1372.
[9] 胡运权.运筹学基础及应用[M]. 北京:高等教育出版社,2004.
[10] 余有明,刘玉树,阎光伟.遗传算法的编码理论与应用[J]. 计算机工程与应用,2008,42(3):86-89.
YU Youming,LIU Yushu,YAN Guangwei. The Coding Theory and Application of Genetic Algorithm[J]. Computer Engineering and Application,2008,42(3):86-89.
(编辑 李丽娟)
Path Planning for Substation Robot Based on Improved Kruskal Algorithm
XU Ping1, LIU Yue2
(1.Jiangmen Power Supply Bureau of Guangdong Power Grid Co., Ltd., Jiangmen 529000, China; 2.School of Automation Engineering, Northeast Electric Power University, Jilin, Jilin 132012, China)
In view of current domestic intelligent inspection robots in substations using navigation mode of magnetic induction lines with radio frequency identification (RFID) technology for designated inspection, this paper studies path planning for inspection points. It firstly considers complexity of the precise algorithm and adopts approximate algorithm for planning inspection path. Focusing on greedy algorithm and local search ideas, it combines heuristic algorithm for improving Kruskal algorithm of minimum support tree. Then, by using MATLAB software, it works out the shortest patrol path and finally obtains the shortest path by means of genetic algorithm. Based on comparison of shortest patrol paths calculated by genetic algorithm and the improved Kruskal algorithm, it shows that the improved Kruskal algorithm has more obvious advantage and is more suitable for inspection path planning for small-scale substations.
substation intelligent inspection; improved Kruskal algorithm; the shortest patrol path
2016-07-07
2016-09-09
10.3969/j.issn.1007-290X.2016.12.002
TP242
A
1007-290X(2016)12-0006-04
徐平(1979),男,山西运城人。高级工程师,工学硕士,从事电气工程自动化工作。
刘悦(1991),女,吉林洮南人。在读硕士研究生,研究方向为鲁棒自适应控制。
