盾构隧道孤石预爆破地表质点峰值振速衰减公式

温智捷， 林从谋， 肖绍清， 张 帆， 殷榕鹏， 杨 宾

(1.华侨大学岩土工程研究所，福建 厦门 361021; 2.福建省隧道与城市地下空间工程技术研究中心，福建 厦门 361021; 3.厦门爆破工程公司，福建 厦门 361021)

盾构隧道孤石预爆破地表质点峰值振速衰减公式

温智捷1, 2， 林从谋1, 2， 肖绍清3， 张 帆1， 殷榕鹏1， 杨 宾1

(1.华侨大学岩土工程研究所，福建 厦门 361021; 2.福建省隧道与城市地下空间工程技术研究中心，福建 厦门 361021; 3.厦门爆破工程公司，福建 厦门 361021)

为了解决盾构隧道孤石预爆破中，不同炸药的性质和药包埋深对质点峰值振动速度的影响，对岩石爆破中地表质点峰值振动速度衰减公式进行了改进，基于叠加原理获得能同时考虑装药结构、岩性特性参数等影响因素的长柱药包峰值振动速度公式，并通过工程实例验证了该公式的有效性。结果表明：长柱形装药地下爆破引起的峰值振动速度不仅受测点与爆源距离影响，也受到装药结构的影响；在装药长度不变条件下，长柱药包的埋深对与爆心水平距离25 m范围内峰值振动速度影响较大，超出25 m范围受到的振动影响程度趋于一致。

地铁；盾构；隧道；衰减公式；孤石爆破；长柱药包；峰值振速

1 引言

在地铁盾构法隧道施工中，地层中常有大块孤石或孤石群，如不提前处理，会对盾构施工造成很大影响。竺维彬等〔1〕总结了爆破预处理孤石施工步骤并进行经济效益分析，该方法已成为预处理孤石的常用手段。地铁隧道多处于城市建筑密集区，周边环境复杂，故爆破处理孤石时需格外注意对周边环境的影响。

目前，爆破处理孤石大多停留在施工方法的研究〔1-4〕上，多数国家预测爆破主要灾害中的爆破峰值振速均使用以下的经验公式〔5〕：

v=KQmRn

(1)

式中：v为爆破峰值振动速度；Q为炸药量；R为测点到爆源中心的距离；K为场地系数；m、n为场地条件的衰减指数，不同地区的m、n的取值不尽相同。

这些公式虽然在表达形式上不同，但最终预测结果差异不大〔6〕。

理论预测方面，卢文波和W.Hustrulid推导出岩石爆破中质点峰值振动速度的衰减公式〔7〕如下：

(2)

(3)

式中：α为爆破振动衰减指数；b为炮孔半径；p0为炮孔内爆生气体的初始压力，在耦合装药的情况下，p0=pe，pe为炸药平均爆轰压力，pe=ρeD2/2(γ+1)，其中ρe为炸药密度，D为炸药爆轰速度，γ为炸药的等熵指数；v0为炮孔壁上质点峰值振速；ρ为介质岩石密度；Cp为纵波在岩石中的波速，Cp=[E(1-μ)/ρ(1+μ)(1-2μ)]1/2，E为岩石弹性模量，μ为泊松比。

多位学者根据实际工程提出以经验公式为基础、考虑高差影响的峰值振速修正公式〔8-10〕。唐廷等〔11〕根据孔穴理论对球形药包条件下地表的运动规律，分析了土中球面入射波和反射波的传播过程，并以数值计算为基础，定量分析了地下爆破的地表运动。此后，程康等〔12〕在前苏联学者萨道夫斯基提出的经验公式的基础上，提出了引入高程的长柱形装药深孔爆破计算公式。吴建与陈士海〔13〕基于Heelan短柱药包爆破振动位移解析解的数值积分，得到了长柱药包爆破产生的围岩介质位移数值解，并认为质点水平和竖向位移在与爆源一定水平距离时达到最大，该距离与药包的长度和埋深有关。孙海利〔14〕对柱状药包进行了数值模拟分析。江向阳等〔15〕通过室内实验，回归得到了适用于柱状药包的经验公式，但其只修正了场地条件系数，亦不能直观反映炸药种类及岩性参数对峰值振动速度的影响。

可以看出，在不同工况中，选择的装药结构多为直径32～90 mm不等的柱形药包。已有的柱形装药经验公式，不能直接反映所使用的炸药性质以及岩石性质参数等因素对峰值振速的影响，因而需要对长柱药包进行进一步探讨。

2 地下长柱药包质点峰值振速

传统质点峰值振动速度的衰减公式无法反应炸药特性、岩性参数及孔径等因素，而式(2)则可将多种因素对质点峰值振动速度的影响综合考虑，且其以柱面波为基础的推导更具理论性〔5〕。而长柱药包爆破过程中，考虑到爆轰速度的影响，炮轰气体压力并非同时作用于孔壁之上，药包的埋深和长度亦为不可忽略的因素。

假设长柱药包由无限个球形药包叠加而成，从底部起爆，底部埋深为h，炮孔填塞长度为h1，药包长度为h2，测点距炮孔中心距离为L(见图1)。

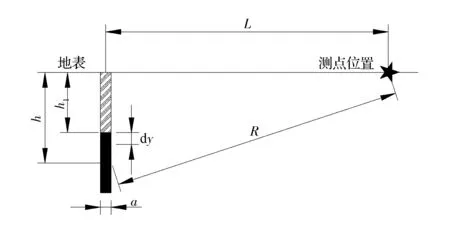
图1 长柱药包爆破计算简图Fig.1 Calculating diagram of long cylindrical charge

在集中装药条件下单个药包质量Q=4πρea3/3，其中ρe为炸药密度，a为药包半径。设炮孔半径为b，在耦合装药条件下b=a，此时：

(4)

将式(4)代入式(2)可得单个球形药包的峰值振速衰减公式：

(5)

把长度为h2的柱状药包分解为若干长度为dy的小单元，q为线装药密度，则每个小单元药包引起的质点振动速度可表示为

(6)

在炸药爆炸时，其自身的爆轰波速度比应力波在岩体介质中传播时的速度快很多，此时，忽略各单元药包引起质点振动速度的时间和方向上的差异，则整个圆柱形药包爆炸所引起的质点振动速度积分可表示为

(7)

(8)

式中：h为药包的埋深，m；h1为炮孔填塞长度，m；R为测点到爆心距离，m。

3 孤石预爆破峰值振速的影响因素

3.1 不同炸药参数对振速的影响

以地下破碎孤石为例，围岩参数〔13〕见表1。

表1 花岗岩计算参数

计算得Cp=5.142×103m/s。取3种岩石乳化炸药：2#岩石乳化炸药，密度为ρe=1.1×103kg/m3，爆轰速度D=3.2×103m/s，炮孔内爆生气体的初始压力p0=1.41×109MPa；1#岩石乳化炸药，密度ρe=1.1×103kg/m3，爆轰速度D=4.5×103m/s，炮孔内爆生气体的初始压力p0=2.784×109MPa；岩石粉状乳化炸药，密度ρe=1 100 kg/m3，爆轰速度D=4.0×103m/s，炮孔内爆生气体的初始压力p0=2.2×109MPa。k和α取值均按GB 6722-2014《爆破安全规程》〔16〕中取最大值，k=150，α=1.5。不同炸药的振速-爆心距变化见图2。

图2 不同炸药情况下的振速-爆心距变化曲线Fig.2 Different cases of explosive vibration velocity-pitch curve

图2(a)中可以看出，式(8)计算得到的峰值振速与使用炸药的种类有关，不同炸药的爆轰速度不同，对振动速度影响较为明显。在外部条件相同的情况下，1#岩石乳化炸药、岩石粉状乳化炸药、2#岩石乳化炸药形成的峰值振速均渐弱，主要的影响因素是不同炸药的爆轰速度。图2(b)中可以看出，用3种不同炸药通过文献〔12〕中给出的公式计算得到的结果相同，不能反映所使用炸药种类对峰值振动速度的影响，且在距爆源较近范围内预测值偏小，在大于50 m范围时与式(8)相近，且不同炸药在40 m外的峰值振速均在2.5 cm/s以下。

3.2 药包埋深对峰值振速的影响

埋深对振速-爆心距的影响曲线见图3。

图3 埋深对振速-爆心距的影响曲线Fig.3 Influence curves of buried depth on velocity-burst center distance

由图3可知，药包埋深对爆心水平距离25 m范围内的峰值振动速度会产生较大影响，由于衰减迅速，爆心水平距离超过25 m范围的峰值振速相差不大。

4 实例验证

4.1 工程概况

实验场地选取厦门市地铁1号线镇海路站基坑，岩层自上而下为碎裂状强风化花岗岩、中风化花岗岩及下部微风化花岗岩，爆源与振动测点相对位置见图4。

图4 爆源-测点位置示意图Fig.4 Diagram of explosion source-measuring point location

爆源炮孔直径90 mm，孔深2 m，每次实验装药1 kg，使用炸药为2#岩石乳化炸药，破碎岩石为中风化及微风化花岗岩，围岩参数见表1。

计算得Cp=5.142×103m/s，其中炸药密度ρe=1.1×103kg/m3，爆轰速度D=3.2×103m/s，炮孔内爆生气体的初始压力p0=1.41×109MPa。

4.2 公式验证

实验所采用的振动测试仪器为TC-4850爆破振动仪以及配套的三向速度传感器，采集过程为多通道数据采集、存储和分析。传感器由石膏固定于测点，测点与爆心距离逐渐接近，实验测试结果见表2。因数据较多，仅列出每次起爆振速测量最大值。

表2 单次爆破监测振速最大值

注：表中为未做减振措施前的振动速度，现场通过减振孔等减振措施将振速控制在国家标准允许范围内以降低对周边房屋的影响。

峰值振动速度公式预测时，k和α取值均按GB 6722-2014《爆破安全规程》〔16〕中取最大值，k=150，α=1.5，计算结果见图5。

图5 公式计算与实测数据对比Fig.5 Comparison of experimental and calculated data

从图5看出，随着爆心距离的增大，峰值振速呈指数趋势下降，预测峰值振速与实测峰值振速得到较好的吻合。改进公式不仅引入了药包埋深因素，也可体现不同种炸药性质对振速的影响。经实测实验数据检验表明，式(8)可以较好地体现峰值振动速度随爆心距变化的衰减规律。

4.3 实例应用

以厦门地铁1号线中山公园站基坑爆破为例，使用2#岩石乳化炸药，孔径70 mm，孔深4.5 m，线装药密度4.47 kg/m。采用数码雷管毫秒间隔多段位起爆，单孔单段最大药量3.4 kg。振动预测与实测情况见图6。

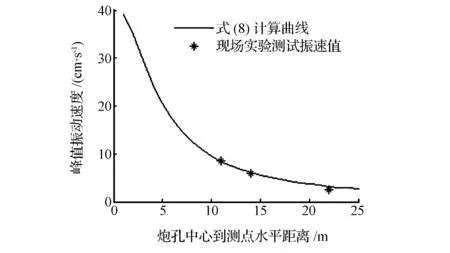
图6 公式计算与实测数据对比Fig.6 Comparison of experimental and calculated data

从实际工程现场测试情况来看，预测公式与实测数值较为一致。

5 结论

(1)长柱形装药地下爆破引起的峰值振动速度不仅受测点与爆源距离影响，也受到装药结构的显著影响，式(8)能较好地体现这一点。

(2)在长柱形装药地下爆破时，其他参数相同的情况下，峰值振动速度的主要影响因素为炸药爆轰速度与炸药埋深，但在药包长度不变条件下，与爆心水平距离超出25 m范围受埋深影响的振动程度趋于一致。

由于工程条件的限制，实验随机统一选取炮底埋深2 m，初步证明了在此埋深条件下该公式的有效性。在实际工程的爆破振动预测中，亦可验证推导公式的有效性。但实验中只使用了2#岩石乳化炸药，对于不同种炸药的预测是否准确仍有待更多进一步验证。

〔1〕 竺维彬，黄威然，孟庆彪，等.盾构工程孤石及基岩侵入体爆破技术研究[J].现代隧道技术，2011，48(5)：12-17.

ZHU Wei-bin, HUANG Wei-ran, MENG Qing-biao，et al. Research on controlled blasting technology for boulders and invading bedrock in shield construction[J]. Modern Tunnelling Technology, 2011，48(5)：12-17.

〔2〕 路耀邦，刘洪震，游永锋，等.海底盾构隧道孤石爆破预处理关键技术[J]. 现代隧道技术，2012,49(5)：117-122.

LU Yao-bang, LIU Hong-zhen, YOU Yong-feng, et al. Keytechniques for the pretreatment of boulder blasting in an under-sea shield-driven tunnel[J]. Modern Tunnelling Technology, 2012,49(5)：117-122.

〔3〕 黄力平.地铁盾构施工遇花岗岩风化球的处理对策及关键技术[J]. 土工技术，2012,26(4)：1-4.

HUANG Li-ping.Metro construction using shielded tunneling in unweathered granite boulder zones[J]. Soil Engineering and Foundation, 2012,26(4)：1-4.

〔4〕 何强，穆大耀，杨通国.孤石爆破安全技术的研究[J]. 矿冶，2014,23(1)：31-33.

HE Qiang, MU Da-yao, YANG Tong-guo, et al. MUda-yao study on safety techniques of boulder blasting[J]. Mining & Metallurgy, 2014,23(1)：31-33.

〔5〕 易长平，冯林，王刚，等.爆破振动预测研究综述[J]. 现代矿业，2011(5)：1-5.

YI Chang-ping, FENG Lin, WANG Gang, et al. A review of research on blasting vibration prediction[J]. Modern Mining, 2011(5)：1-5.

〔6〕 MANOJ K，T N. Singh evaluation of blast-induced ground vibration predictors[J].Soil Dynamics and Earthquake Engineering，2007(27):116-125.

〔7〕 卢文波，HUSTRULID W.质点峰值振动速度衰减公式的改进[J]. 工程爆破，2002，8(3)：1-4.

LU Wen-bo, HUSTRULID W. An improvement to the equation for the attenuation of the peak particle velocity[J]. Engineering Blasting，2002，8(3)：1-4.

〔8〕 宋光明，陈寿如，史秀志. 露天矿边坡爆破振动监测与评价方法的研究[J].有色金属：矿山部分，2000(4)：24-27.

SONG Guang-ming, CHEN Shou-ru, SHI Xiu-zhi. Study on monitoring and evaluation method of blasting vibration of slope blasting in open pit mine[J]. Nonferrous Metals：Mining Section, 2000(4):24-27.

〔9〕 刘美山，吴从清，张正宇.小湾水电站高边坡爆破震动安全判据试验研究[J].长江科学院院报，2007,24(1)：40-43.

LIU Mei-shan , WU Cong-qing, ZHANG Zheng-yu, et al. Experimentation on judging standard of blasting vibration safetyin high slope excavation of Xiaowan hydropower station[J].Journal of Yangtze River Scientific Research Institute，2007,24(1)：40-43.

〔10〕 许海亮，张继春，杨红，等.钻孔爆破振动速度计算公式及其简化的探讨[J]. 同济大学学报(自然科学版)，2007,35(7)：899-903.

XU Hai-liang, Zhang Ji-chun, YANG Hong, et al. Investigation on calculating formula of vibration velocity in drilling blasting and its simplification[J]. Journal of Tongji University: Natural Science，2007,35(7)：899-903.

〔11〕 唐廷，王明洋，葛涛. 地下爆炸的地表运动研究[J]. 岩石力学与工程学报，2007，26(S1)：3 528-3 532.

TANG Ting， WANG Ming-yang, GE Tao. Study on ground movement of underground explosions[J]. Chinese Journal of Rock Mechanics and Engineering，2007，26(S1)：3 528-3 532.

〔12〕 程康，沈伟，陈庄明，等.工程爆破引起的振动速度计算经验公式及应用条件探讨[J]. 振动与冲击，2011，30(6)：127-129.

CHENG Kang, SHEN Wei, CHEN Zhuang-ming, et al. Inquiry into calculation formula for vibration velocity induced by engineering blasting and its application conditions[J]. Journal of Vibration and Shock，2011，30(6)：127-129.

〔13〕 吴建，陈士海.长柱药包爆破振动位移特性研究[J]. 工程爆破，2014，20(5)：50-54.

WU Jian, CHEN Shi-hai. Study on the displacement characteristics of blasting vibration about long cylindrical charge[J]. Engineering Blasting，2014，20(5)：50-54.

〔14〕 孙海利. 基于ANSYS/Ls-dyna仿真模拟对条形药包爆破地震效应的研究[D]. 西安：长安大学，2015.

SUN Hai-li. The study of linear charge blasting seismic effect based on ANSYS/Ls-dyna simulation[D]. Xi'an: Chang'an University, 2015.

〔15〕 江向阳，颜事龙，刘伟，等. 柱状药包爆炸波传播规律的试验分析[J]. 重庆大学学报，2015,38(4):121-127.

JIANG Xiang-yang, YAN Shi-long, LIU Wei, et al. Experimental analysis of the law of explosive wave of cylindrical charge[J]. Journal of Chongqing University, 2015,38(4):121-127.

〔16〕 国家安全生产监督管理. 爆破安全规程：GB 6722-2014[S]. 北京：中国标准出版社，2014.

State Administration of Work Safety. Safety regulations for blasting：GB 6722-2014[S]. Beijing: China Standards Press, 2014.

Attenuation formula of peak vibration velocity of ground particle in pre-blasting of boulder in shield tunnel

WEN Zhi-jie1,2， LIN Cong-mou1， XIAO Shao-qing3, ZHANG Fan1,YIN Rong-peng1，YANG Bin1

(1.Research Institute of Geotechnical Engineering，Huaqiao University，Xiamen 361021,Fujian,China;2.Fujian Tunnel and Urban Underground Space Engineering Technology Research Center，Xiamen 361021,Fujian,China;3.Xiamen Blasting Engineering Company, Xiamen 361021,Fujian,China)

In order to solve the influence of the properties of different explosives and the burial depth on the peak vibration velocity of the particle in the pre-blasting tunnel boulder, the attenuation formula of the peak velocity of the surface particle in rock blasting was improved. Based on the superposition principle, charge structure, and lithological characteristics of the rockburst, the vibration velocity formula of the long pillar was also given. The results showed that the peak vibration velocity of the long columnar charge was not only affected by the distance between the measured point and the burst source, but also by the structure of the charge. Under the same charge length, the depth of the long cylindrical charge 25 m in the range of the impact on the peak vibration velocity was greater, the impact on vibration was basically the same over 25 m.

Subway; Shield; Tunnel; Boulder blasting; Long cylindrical charge; Peak vibration velocity

1006-7051(2016)06-0013-05

2016-10-20

福建省自然科学基金计划资助项目(2014J01197)；华侨大学研究生科研创新能力培育计划资助项目(1400204006)

温智捷(1990-)，男，在读硕士，从事岩土工程与实验研究。E-mail: wzj0313@qq.com

林从谋(1957-)，男，博士，教授，从事岩土工程与地下结构的科研及教学。E-mail: cmlin@hqu.edu.cn

TU447

A

10.3969/j.issn.1006-7051.2016.06.003