基于多井压裂数据的煤岩水平地应力反演模型建立及应用

袁 征 王杏尊 黄 杰 郭布民 邢云龙 王绪性

(中海油田服务股份有限公司油田生产研究院，天津 300450)

基于多井压裂数据的煤岩水平地应力反演模型建立及应用

袁 征 王杏尊 黄 杰 郭布民 邢云龙 王绪性

(中海油田服务股份有限公司油田生产研究院，天津 300450)

通过分析不同坐标系下井壁应力分布状态，结合岩石起裂准则推导出裂缝破裂压力的具体形式，在此基础上建立了破裂压力与水平主应力的超定方程组；通过对方程组在矩阵形式下分离变量、求导等，最终建立了水平地应力反演模型。基于此模型对柿庄南某区块的水平地应力值进行了计算，结果显示：本区最大、最小水平主应力与上覆岩层压力值相近，三者应力差不超过3MPa，且最小水平主应力最弱，反演结果与裂缝监测数据相符。

水力压裂 破裂压力 水平地应力 反演模型 超定方程组

1 模型建立

建立煤层气井井眼坐标系OXYZ，如图1所示。为建立井壁应力坐标系与地层三向主应力之间的联系，在沿井轴方向上的某点为原点建立最大、最小主应力及上覆岩层压力的0123坐标系。若井眼以最大水平主应力标定的方位角为α,井斜角为β，则两坐标系存在如下几何关系：首先沿上覆岩层压力旋转方位角α，再将上覆岩层压力向井轴方向旋转β。

图1 井眼应力坐标系转换关系示意图

坐标系0123与坐标系OXYZ之间的转换关系可以通过下列矩阵变换得到：

(1)

进而可以得到最大水平主应力σH、最小水平主应力σh与X、Y方向上应力分量关系式如下：

(2)

式中，σx为X方向的应力分量；σy为Y方向的应力分量；σv为岩石上覆岩层压力。

根据坐标系之间的转换关系，井壁岩石柱坐标系下的周向应力在直角坐标系下的转换关系如下：

σθθ=(σx+σy)-2(σx-σy)cos2θ-4τxysin2θ-Pb

(3)

式中，σθθ为沿井壁方向的周向应力；τxy为XY面的剪应力；Pb为井底静液柱压力。

考虑储层内部孔隙压力的影响，同时忽略剪应力对周向应力作用时，水力裂缝起裂准则：当最大周向拉伸应力大于岩石抗拉强度时裂缝开始起裂，裂缝起裂公式如下：

-σt=σθθ-pp

(4)

结合式(3)、(4)，考虑到不同井眼井斜角和方位角，0123坐标系在OXYZ坐标系内的应力分量显然不同，分类整理，可得到水力压裂井眼起裂方程的两种形式，即Kirch简化方程如下：

(5)

式中，pp为储层孔隙压力；pf为地层起裂最低井底施工压力。

将式(2)带入到式(5)。分离变量整理可得

(6)

分析上述公式可以看出，破裂压裂、地层孔隙压力、岩石抗拉强度、井斜角、方位角以及上覆岩层压力参数均可以从测井、压裂施工中获取，仅最大、最小水平主应力为未知参数。上述公式可简写为：

p=a·σH+b·σh

(7)

显然存在两组数据可即可得出最大、最小主应力，受测井及施工参数的录取存在一定误差，计算值与实际值存在一定误差。显然可增加同地区同层位的施工数据来降低误差值。当存在n组数据时便可得到如下矩阵形式的超定方程组：

简写为P=C·X

(8)

当方程的个数大于未知数的个数时将演变成超定方程组，并且现场施工数据很慢满足方程组相容性，然而应力最优解应使误差最小。借鉴最小二乘法思想，定义矩阵方程的方差如下：

e2=(P-C·X)T(P-C·X)

(9)

根据矩阵知识上式对XT、X求导具有等价性，对上式求导，方差在最小点时导数值为0，结果如下：

(10)

进而得：

X=(CTC)-1·CT·P

考虑到深度的影响，在计算过程中应力用当量密度表示。同时考虑到实际方位角与本文出现的方位角存在一定的差别，在计算过程在首先要给出最大或者最小水平地应力的方向，并结合实际井斜角φ得到上述公式中标定的井斜角α。

通过上述模型可以看出，在计算之前无法判断应力分量σx、σy的大小。因此每组参数都会得出两个形式的方程，当存在n组数据时，显然可以得出2n个形式相同的方程组，进而可以得出2n组解，其中可使方差最小的解可认为最优解。

2 沁水盆地南某区块地应力计算

沁水盆地为我国煤层气勘探开发的主力区，水裂压裂施工为认识和分析煤层气产层提供了丰富的数据。本文选取沁水盆地南部柿庄南某区块的6口井为例，计算此地区的地应力值。6口煤层气井的靶点间距在300m左右，埋深在800～900m之间，属于二叠系下统山西组。裂缝监测结果显示最大主应力方向与正北方向的夹角为75°，煤岩抗拉强度1MPa，具体参数见表1。

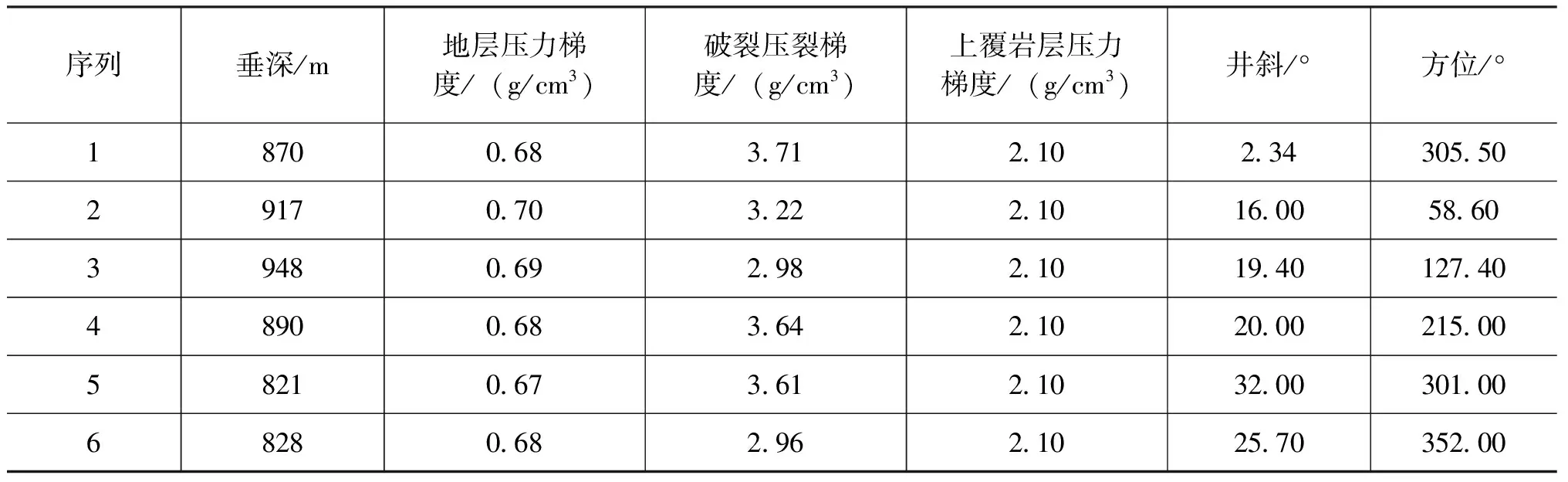
表1 柿庄南6口井压裂基本参数表

表2 最大、最小水平主应力计算结果表

3 地应力计算结果

计算得此地区最大水平主应力梯度2.14g/cm3、最小水平主应力梯度1.87g/cm3、上覆岩层压力梯度2.10g/cm3(见表2)。结果显示：最小水平主应力小于上覆岩层压力，最大、最小水平主应力接近，各应力差小于3MPa。对于上述应力状态，水力压裂时易产生垂直裂缝和多裂缝现象，这与裂缝监测结果相一致。

[1] 李志明,张金珠. 地应力与油气勘探开发[M].北京：石油工业出版社，1997:113-121.

[2] 景锋.我国原位地应力测量与地应力场分析研究进展[J].岩土力学,2011,2(32):51-58.

[3] 张重远,吴满路等.地应力测量方法综述[J]. 河南理工大学学报,2012,3(31):305-311.

[4] 廖永远,罗东坤,李婉棣等.中国煤层气开发战略[J]. 石油学报,2012,6(33):1098-1102.

[5] 罗陶涛.沁水盆地煤岩储层特征及压裂增产措施研究[D].成都理工大学,2010:50-74.

[6] 曹代勇,张守仁,穆宣社等.中国含煤岩系构造变形控制因素讨论[J]. 中国矿业大学学报,1999,1(28):26-29.

(责任编辑 刘 馨)

Establishment and Application of Horizontal In-situ Stress Inversion Model in Coal Rock Based on Multiple Fracturing Data

YUAN Zheng, WANG Xingzun, HUANG Jie, GUO Bumin, XING Yunlong, WANG Xuxing

(Production Optimization Department Research Institute, China Oilfield Services Ltd., Tianjin 300450)

An overdetermined equation about fracture pressure and horizontal in-situ stress is established based on analyzing stress distribution on borehole wall and deducing definite formation of fracture pressure. In-situ stress inversion model is given with some settle on the equation set, such as variables separation, derivation. Horizontal in-situ stresses of south Shizhuang is calculated based on the inversion model, and the result shows that the overburden pressure is similar with horizontal in-situ stresses in this area, and difference value under 3MPa among the three stresses. Minimum horizontal in-situ stress value is the smallest, in accordance with crack monitoring data. Keywords:Hydraulic fracture; fracture pressure; horizontal in-situ stress; inversion model; overdetermined equation

袁征，男，压裂工艺工程师，现从事非常规致密气、煤层气水力压裂相关工作。