Horava引力下Park黑洞的电磁扰动

王春艳，马 媛，董 亮

(1. 渤海大学 数理学院, 辽宁 锦州 121013； 2. 大连理工大学 物理与光电工程学院, 辽宁 大连 116024)



Horava引力下Park黑洞的电磁扰动

王春艳*,1,2，马 媛1，董 亮1

(1. 渤海大学 数理学院, 辽宁 锦州 121013； 2. 大连理工大学 物理与光电工程学院, 辽宁 大连 116024)

利用三阶WKB近似方法,计算Horava引力中Park黑洞电磁扰动的似正规模频率. 研究发现,似正规模是复频率且与Park黑洞的时空背景参数ΛW,w以及l和n有关.复频率的实部随着ΛW的减小而减小,虚部绝对值是先增加后减小.态参数w对似正规模频率的影响非常小.与标准SdS黑洞电磁扰动的数值结果比较发现,电磁扰动在Horava引力下Park黑洞时空中衰减的较慢.

电磁扰动;WKB近似;Horava引力;Park黑洞

0 引言

Horava引力是一个新的四维引力理论模型〔1-3〕,在红外低能区域,该理论自然流向爱因斯坦广义相对论,但在紫外高能区域中,该理论是非相对论的,并且由于高阶空间曲率项的引入破坏了洛伦兹对称性,从而可以避免广义相对论的重整化困难.该理论在宇宙学和黑洞方面已经被广泛研究〔4-8〕.

黑洞时空中的似正规模因为携带有黑洞的特征信息(质量、电荷量和角动量),而被誉为黑洞的“特征声音”.此时,波的频率为复数且不依赖于微扰源的初始条件,只与黑洞背景时空的参量有关〔9-11〕.因此,对黑洞在各种微扰场下似正规模的研究〔12-18〕,将为判断黑洞是否存在提供有利的证据.

本文利用三阶WKB近似方法计算Horava引力下Park黑洞的电磁扰动的似正规模频率.

1 Park黑洞和电磁扰动

在Horava引力下,引入宇宙学常数和细致平衡条件,作用量为〔8〕

(1)

其中Kij是外曲率张量,Cij是Cotton张量,κ,v,λ,μ,ΛW,w,则分别是常参数.最后一项是细致平衡条件.

Mu-InPark〔8〕得到了一组静态球对称的一般解.当考虑渐进deSitter时空时，有ΛW>0且w<0，则

Horava引力下的Park黑洞解的度规线元形式如下:

(2)

其中

(3)

M是Park黑洞的质量.

在真空中,电磁场扰动满足的Maxwell方程为〔9〕

(4)

其中,Fμv是黑洞时空背景下电磁场逆变张量,其协变张量Fμv满足Fμv=Av,μ-Aμ，v.电磁势Aμ可以展开成四维矢量球谐函数〔20〕.

(5)

等式右侧第一列宇称为(-1)l+1,第二列宇称为(-1)l,其中l是角量子数,m是磁量子数.

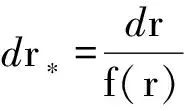
(6)

上式中ψ(r)=alm(当宇称为(-1)l+1),ψ(r)=r2/l(l+1)(-iωhlm-dflm/dr)(当宇称为(-1)l)〔20〕.

有效势函数V(r)满足

(7)

从(7)式可以看出电磁场的有效势与宇宙学参数ΛW,态参数w和微扰场的角量子数l有关,并且在r的取值范围内将一直是以势垒的形式存在.图1和图2分别给出了有效势V(r)随着l和ΛW的变化关系.从图中可见,随着l的增加势垒的峰值增加,峰值所在的位置沿着x轴向右边移动.有效势的势垒峰值随着ΛW,的增加而增加,但峰值所在位置则向左移动.

图1 电磁场势能随l的变化关系,比较l=4时Park黑洞与SdS黑洞的势能曲线 图2 电磁场势能随r的变化关系,ΛW分别取0.1,0.01,0.0001

2 数值方法和结论

利用三阶WKB近似〔21〕计算Horava引力下的Park黑洞的电磁扰动的似正规模频率,这里我们令M=1.基本计算公式为

(8)

(9)

(10)

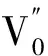
表1给出了Horava引力下Park黑洞电磁扰动的似正规模频率的数值结果.我们发现这些复频率的虚部均是负值,这意味着似正规模随时间作指数衰减,并且在很晚的时候,指数衰减将变成幂率衰减.这现象说明该黑洞在电磁扰动下随时间的演化是趋于稳定的.表2给出了Park黑洞随着参数w的变化关系.另外,为了方便比较,表3给出了SdS黑洞电磁扰动的似正规模频率.图3直观的给出了电磁扰动似正规模频率的实部与虚部变化曲线.

表1 Horava引力下Park黑洞电磁扰动的似正规模频率,w=-2

表2 Horava引力下Park黑洞电磁扰动的似正规模频率,ΛW=0.0001,n=0

表3 SdS黑洞电磁扰动的似正规模频率,ΛW=0.0001

3 结论

本文利用三阶WKB近似方法计算了在Horava引力下的Park黑洞电磁扰动的似正规模频率.从所得的数值结果我们发现,对于固定的w,l和n,随着ΛW的减小,电磁扰动似正规模频率的实部也减小,但是虚部绝对值是先增加后减小,并且当ΛW足够小的时候,似正规模频率将几乎不受影响.其次,从表2可以看出,态参数w对似正规模频率的影响非常小.另外,当其它参数固定时,似正规模实部和虚部绝对值随着角量子数l的增加而增大.最后,与经典的SdS黑洞电磁扰动数值结果比较发现,在Park黑洞中电磁扰动似正规模的实部比较大,而虚部绝对值比较小,这一现象表明,Horava引力下Park黑洞背景时空中电磁扰动振荡的比较快而衰减的较慢.

〔1〕HORAVAP.QuantumgravityataLifshitzpoint〔J〕.PhysicalReviewD，2009, 79(8): 2155-2161.

〔2〕HORAVA P. Spectral dimension of the universe in quantum gravity at a lifshitz point〔J〕. Physical Review Letters, 2009, 102(16): 161301 (1-4).

〔3〕HORAVA P. Membranes at quantum criticality〔J〕.JHEP，2009，3(3)： 1-33.

〔4〕LU H, MEI J, POPE C N. Solutions to Horava gravity〔J〕. Physical Review Letters, 2009, 103(22): 7450-7462.

〔5〕KEHAGIAS A, SFETSOS K. The black hole and FRW geometries of non-relativistic gravity〔J〕.Physics Letters B, 2009, 678(1): 123-126.

〔6〕MYUNG Y S. Entropy of black holes in the deformed Horava-Lifshitz gravity〔J〕. Physics Letters B, 2010, 684(2-3): 158-161.

〔7〕WEI S W, LIU Y X, WANG Y Q, et al. Thermodynamic geometry of black hole in the deformed Horava-Lifshitz gravity〔J〕. EPL, 2010, 99(2): 21-24.

〔8〕PARK M I. The black hole and cosmological solutions in IR modified Horava gravity〔J〕. Journal of High Energy Physics, 2009, 2009(9): 1295-1301.

〔9〕CHANDRASEKHAR S, DETWEILER S. The quasinormal modes of the schwarzschild black hole〔J〕. Proceedings of the Royal Society A Mathematical Physical, 1975, 344(1639): 441-452.

〔10〕REGGE T, WHEELER J A. Stability of a schwarzschild singularity〔J〕. Physical Review, 2010, 108(108): 1063-1069.

〔11〕VISHVESHWARA C V. Scattering of gravitational radiation by a Schwarzschild black-hole〔J〕. Nature, 1970, 227(5261): 936-938.

〔12〕CARDOSO V, LEMOS J P S, YOSHIDA S. Quasinormal modes and stability of the rotating acoustic black hole: numerical analysis〔J〕. Physical Review D, 2004, 70(12): 317-324.

〔13〕BERTI E, CARDOSO V. Quasinormal ringing of Kerr black holes: The excitation factors〔J〕. Physical Review D, 2006, 74(10): 711-717.

〔14〕FERNANDO S, CORREA J. Quasinormal modes of bardeen black hole: scalar perturbations〔J〕. Physical Review D, 2012, 86(86): 329-346.

〔15〕GAMMATTEOL M. Dirac quasinormal frequencies in Schwarzschild-AdS space-time〔J〕. Physical Review D, 2004, 71(2): 430-437.

〔16〕CHEN S, JING J. Quasinormal modes of a black hole in the deformed Horava-Lifshitz gravity〔J〕. Physics Letters B, 2010, 687(2-3): 124-128.

〔17〕董亮, 王春艳，马媛. Horave引力理论中Park黑洞有质量标量场的似正规模〔J〕. 渤海大学学报(自然科学版), 2016(1): 19-23.

〔18〕BRILL D, WHEELER J. Interaction of neutrinos and gravitational fields〔J〕. Review of Modern Physics, 1957, 29(29): 465-479.

〔19〕WHEELER J A. GEONS. Phys. Rev., 1957, 97(2): 511-536.

〔20〕RUFFINI R. In Black Hole: les Astres Occlus. New York: Gordon and Breach Science Publishers. 1973.

〔21〕IYER S, WILL C M. Black-hole normal modes: A WKB approach. I,II. Foundations and application of a higher-order WKB analysis of potential-barrier scattering〔J〕. Phys. ReV. D, 1987, 35(12): 3621-3636.

Electromagnetic perturbation of Park black hole in Horava gravity

Wang Chun-yan1,2, MA Yuan1, DONG Liang1

(1. College of Mathematics and Physics, Bohai University, Jinzhou 121013, China; 2. School of physics and optoelectronic technology, Dalian University of Technology, Dalian 116024, China)

In this paper we have evaluated the quasinormal modes of the electromagnetic perturbation of Park black hole in the Horava gravity, using the third order WKB approximation method. One can find that the quasinormal modes frequencies relate to parameters ΛW、wandl、nof Park black hole .The real parts of complex frequencies decrease with ΛWdecreasing, while the magnitude of the imaginary parts decrease after increase. The influence of parameterswon the quasinormal modes frequency is so little. Moreover, by comparing the numerical results of electromagnetic perturbation with the case of SdS black hole, we find that the electromagnetic field oscillates more faster but damps more slower in Horava gravity.

electromagnetic perturbation; WKB approximation; Horava gravity; Park black hole

2016-04-08.

国家自然科学基金项目(No：11271055).

王春艳(1980-)，女，博士，副教授，主要从事黑洞物理方面的研究.

loveyan-zi@126.com.

P145. 8

A

1673-0569(2016)04-0313-05