浅析动量守恒定律结论及两推论在解题过程中的应用

李玲玲●

江苏省射阳县第二中学(224300)

浅析动量守恒定律结论及两推论在解题过程中的应用

李玲玲●

江苏省射阳县第二中学(224300)

动量守恒定律是高中物理重要的物理规律之一，在实际解题过程中有着广泛的应用.从对动量守恒定律的考查内容可以看出，对动量守恒定律推论的考察比例要远大于对定律本身的考察.本文我将着眼于动量守恒定律的两个推论，对其在实际解题过程中的应用进行讨论.

高中物理;动量守恒;推论;解题应用

动量守恒定律是解决高中物理问题的三大工具之一，作为物理教学的重点，在动量守恒定律的基础上，必须强调对其推论教学的重要性，从而提高学生的解题能力.对于动量守恒定律，其实质就是在不受外力或合外力为零的系统中，该系统的总动量保持不变.在此基础上，我们从同一方向上的受力和同一系统的受力这两个角度出发，推广得到了动量守恒定律的两个推论，并对其应用实践展开探究.

一、动量守恒定律推论1

由动量守恒定律的概念可知，动量是一个矢量，其同时具有大小和方向两个特性.动量守恒定律指的是在某一不受力或合外力为零的系统中，该系统的动量保持不变，也可以表述为在无外力作用的系统内，不同物体之间的动量相互转化，但其总和保持不变，这就是动量守恒定律.于是，我们从动量守恒定律的矢量性角度出发，单纯的从某一方向出发，对该方向上的动量守恒进行探究，从而可以得到动量守恒定律的推论1：在某一方向上，该系统不受到外力或合外力为零，在于其垂直的方向上受到的合外力不为零，则在合外力为零或不受外力的方向上，该系统的动量守恒.

例1在光滑水平地面上，有一小车，其质量为m1，用长L的细绳将质量为m2的小球挂在车支架上.开始时，小球和车均处于静止状态，现突然给小球一个水平向左的速度，试求小球在摆动过程中细绳与竖直方向的最大夹角是多少？

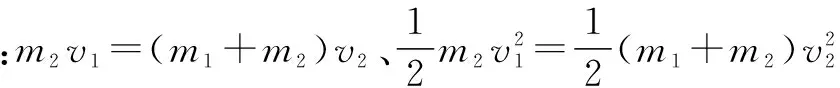
点评 在本题中，我们可以将小球和细绳视为一套系统，当小球向左摆动时，小车同样处于向左运动的状态.在此系统中，垂直系统方向在该运动过程中存在向上的合力，同时，该系统在水平方向上不受外力.因此，可以利用推论1得到该系统在此运动过程中的水平方向上动量守恒.最后，利用动量守恒公式即可实现本题的求解.

二、动量守恒定律推论2

在动量守恒定律使用过程中，若是考虑整个系统的动量守恒，我们只需要研究系统外力的作用.若是该系统不受外力或合外力为零，则不需要考虑系统间内力，且系统满足动量守恒定律.此时，系统的总动量不会受到系统内物体间相互动量的转换影响，系统的动量依然守恒.于是，我们可以得到动量守恒定律推论2：当两个或以上物体间的相互作用力不存在，或者受到其他物体的作用力矢量和为零，则我们可以将该系统视为动量守恒系统.

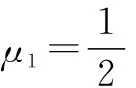
点评 本题的难点在于判断动量守恒的过程，对小球、弹簧、细绳及桌面组成的系统，在脱离前，两球受到的摩擦力大小相等、方向相反，满足动量守恒定律.在脱离后，两个小球受到摩擦力与重力，直到两小球静止前，两者之间均无相互作用力，则可以认为两小球受到的外力矢量和为零.由推论2可知，两小球满足动量守恒定律.此后，利用动量守恒的基本公式即可得到欲求的速度.

三、动量守恒定律结论

由动量守恒定律的内容可知，当系统受到的合外力为零时，系统的总动量守恒，且系统质心的速度保持恒定不变.同时，若是系统在某一方向上受到的合外力为零，则系统在该方向上的动量守恒，系统质心在这一方向上的速度不变.这是动量守恒定律的一个重要结论，在很多实际问题中，这个结论对解题有着显著的作用.

例3 如图所示，有一质量为M的密闭气缸放置在光滑水平面上，中间设置有一隔板P，隔板右边是真空，隔板左边是质量为m的高压气体，若将隔板瞬间抽去，则气缸的运动方式是？

解析 在该系统中，抽去隔板之前，隔板两侧的气体所受到的合外力均为零，因此可知，系统的质心位置保持不变.当隔板抽去后，受到压强影响，气体必然会向右扩散，则气体的质心必然也会向右移动.此时，利用动量守恒定律的结论，为了使系统的质心位置不变，因此，气缸必须向左移动.当气体充斥整个汽缸之后，隔板的运动也就会停止.

点评 此类题型是动量守恒定律的特殊题型，考察的是学生对动量守恒定律的结论的掌握.该结论将动量守恒原理与系统质心概念相联系，在解决与质心相关的问题时，该结论会有显著的作用.

总之，动量守恒定律是高中物理教学中的重点和难点，学生们对深入掌握其结论和推论存在一定的障碍.对此，我们必须将对应的结论和推论带入到实际题目中，在题目的求解过程中渗透动量守恒定律的概念和性质教学.

G632

B

1008-0333(2016)34-0059-01