悬挂式单轨交通系统曲线段合理轨距研究

胡燚斌，肖杰灵，林红松，王平

(1．西南交通大学高速铁路线路工程教育部重点实验室，四川成都610031; 2．中铁二院工程集团有限责任公司，四川成都610031)

悬挂式单轨交通系统曲线段合理轨距研究

胡燚斌1，肖杰灵1，林红松2，王平1

(1．西南交通大学高速铁路线路工程教育部重点实验室，四川成都610031; 2．中铁二院工程集团有限责任公司，四川成都610031)

基于多体动力学理论，建立了多自由度悬挂式单轨列车系统动力学模型，并通过数值积分求解车体的动力响应，进而研究不同轨距下，悬挂式单轨列车的曲线通过能力，即车辆通过曲线时的车体加速度大小及导向轮导向力大小。结果表明:曲线通过时，悬挂式单轨车辆横向加速度随轨距的增大而增大，当轮轨游间≥8 mm，即轨距≥788 mm时，车体横向加速度超过了舒适度指标(0.9 m/s2);导向轮导向力则随着轨距的增大，先减小后增大。根据轨距对车体响应及导向轮受力的影响，并充分考虑工程现场的实际情况，最终给出了悬挂式单轨交通系统的合理轨距建议值为784～788 mm。

悬挂式单轨交通;多体动力学;轮轨游间;轨距

悬挂式单轨交通系统属于单轨交通的一种，依据车辆转向架与轨道梁的不同，可将悬挂式单轨交通系统分为对称式和非对称式2类。对称式悬挂单轨多为胶轮-走行轨系统。相对于非对称式单轨交通，对称式单轨具有噪音小、工期短、稳定性高、受环境因素影响小等特点，是现代悬挂式单轨交通的发展方向。本文悬挂式单轨交通系统均指对称式悬挂单轨交通系统。

目前，国内外对悬挂式单轨交通虽有一定的研究，但我国尚未建有悬挂式单轨交通系统，相关的标准规范也处于空白。文献［1］总结了德国多特蒙德、杜塞尔多夫悬挂式单轨交通的特点。文献［2］综述了悬挂式单轨车辆的发展及现状，并比较了悬挂式单轨交通的车辆性能。文献［3-5］通过建立动力学模型，计算分析了悬挂式单轨的车辆动力学性能。轨道梁是悬挂式单轨交通系统的重要组成部分，轨道梁不仅需要为车辆走行轮提供走行面，还需为导向轮提供导向面，约束车辆系统的横向运动。在曲线通过时，车辆的离心运动将产生较大的横向加速度，故合理的轨距值无论对于车辆运行，还是对于轨道梁的合理受力都有着重要的影响。文献［6］研究了悬挂式单轨车辆的横向稳定性。但上述研究并未最终确定悬挂式单轨合理游间和合理轨距。由于悬挂式单轨交通系统与传统轨道交通系统差异较大，故传统的轨距加宽原理并不适用。为研究轨距对车辆运行平稳性以及轨道梁横向受力的影响，本文基于多体动力学理论，建立了多自由度的动力学模型，设立不同工况进行仿真计算、分析，并最终确定曲线段悬挂式单轨交通系统的合理轨距值。

1 轨距加宽原理

1.1 传统轨距加宽原理

对于普通铁路，由于轨道游间的存在，机车车辆转向架通过曲线轨道时，能以下列4种不同的几何内接方式通过:①斜接通过;②自由内接通过;③楔形内接通过;④正常强制内接通过。前3种内接方式见图1。

图1 机车车辆通过曲线的内接形式

传统轨距加宽原则为保证大多数车辆能以自由内接的形式通过曲线;保证不出现楔形内接形式，但允许以正常强制内接形式通过;保证车轮不跑道。

依据车辆运行条件，轮轨自由内接所需轨距sw为

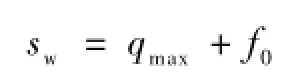
式中:qmax为最大轮对宽度;f0为外矢距［7］。

1.2 悬挂式单轨轨距确定原理

相比普通铁路，悬挂单轨轨道结构特殊。如图2所示:其底部为走行面，供走行轮行驶;侧面为导向面，能够提供平衡离心力的横向力，限制车辆的横向位移。悬挂铁路车辆转向架(见图3)的构造也与普通车辆转向架有很大差异，在转向架各个角上装有导向轮，可为车辆行驶提供导向力，导向轮外边距为780 mm。悬挂式单轨走行轮、导向轮均为橡胶实心轮胎，可进行压缩，但由于刚度较大，所以压缩量有限。轨道梁内侧宽度即为悬挂式单轨轨距，为保证车辆正常通过，应大于等于导向轮外边距，即轨距≥780 mm。

从轨道、转向架结构以及轮轨接触关系可以看出，悬挂式单轨轨道较传统铁路轨道有极大的差别，且二者的材料、线路差异也较大，故传统轨距加宽原理不再适用于悬挂式单轨中，需采用新的方法确定悬挂式单轨曲线段轨道轨距。

参考结构与悬挂式单轨较为接近的跨座式单轨，其曲线通过情况如图4所示。从中可以看出对于跨座式单轨，假设直线段导向轮内侧宽度与轨道外侧宽度一致，在不考虑导向轮弹性的前提下，当单个转向架进入曲线时，2个导向轮内侧宽度为曲线轨道两侧距离的最小值，所以必然要出现压缩［8］。因此对于跨座式单轨，必须要减小曲线段轨道梁轨距，以保证车辆正常通过。

对悬挂式单轨来说，其转向架置于轨道内部(见图5)，即在理想状态下，导向轮外侧距为曲线轨道两侧距离的最小值，所以从理论上来说，悬挂式单轨曲线段不设置游间，即不考虑轨道加宽，并不会导致其无法通过。但是制造、安装误差以及轨道不平顺的存在，加之转向架可能出现转动，都意味着悬挂式单轨轨道必须存在游间才能保证其通过，而轨道游间不仅影响单轨列车的通过性能，还直接影响车体所受横向加速度以及导向轮的导向力，并对后期的轨道磨耗产生影响。游间过小，可能导致在轨道不平顺下，车辆无法顺利通过曲线段，亦可导致磨耗过大;而游间过大，可能导致车体横向加速度增大，运行平稳性无法得到保证。故对于悬挂式单轨交通系统，确定曲线段合理游间，设置合理轨距就显得十分重要。本文将建立动力学模型，分析不同轨距下，车辆的曲线通过性能，并最终得到合理的轨距值。

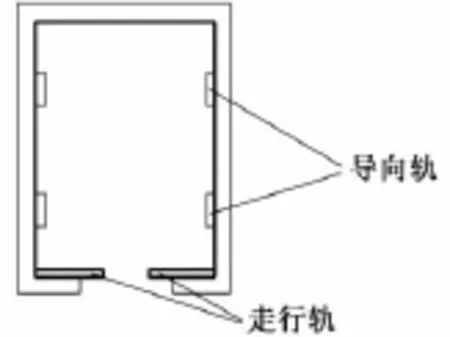
图2 悬挂式单轨轨道结构

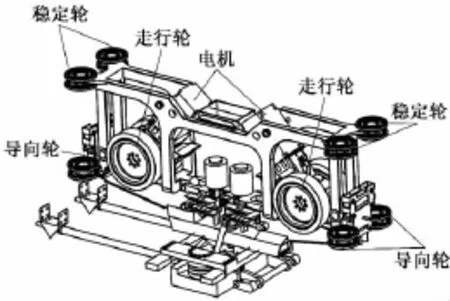
图3 悬挂式单轨转向架

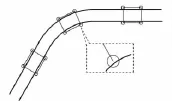
图4 跨座式单轨曲线通过情况

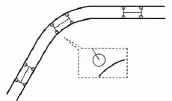
图5 悬挂式单轨曲线通过情况

2 动力学模型的建立

悬挂式单轨车辆模型主要分为3部分:转向架、摆动装置、车体。转向架与车体之间由摆动装置连接。

将模型简化后如图6所示，可以看出摆杆与转向架之间存在摇头方向自由度，而与车体之间存在侧摆方向自由度。

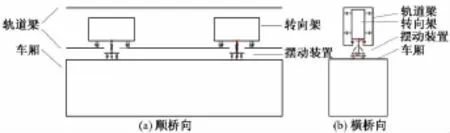
图6 悬挂式单轨列车平面模型

部分车辆重要参数取值见表1。

表1 部分车辆重要参数取值

运用多体动力学软件，建立悬挂式单轨车辆动力学模型，并在各个导向轮上布置了导向力的测点，同时在车厢底部布置前、中、后3个加速度测点，如图7所示。

图7 悬挂式单轨车辆动力学模型

3 计算工况及结果

为了确定曲线段的合理轨距值，以圆曲线半径为50 m，侧向通过速度取为20 km/h，设置5种工况见表2，分析游间对车辆走行性能的影响。在直线段，默认轨距为780 mm，不设置游间。

表2 工况设置

计算时不考虑轨道不平顺。通过动力学软件，采用数值积分的方法，进行动力学仿真计算，结果如图8、图9、图10、图11所示。

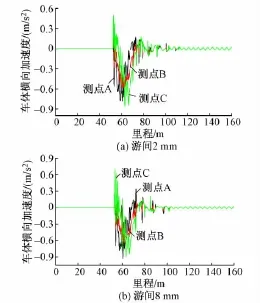
图8 不同工况下车体横向加速度

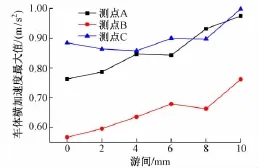
图9 不同工况下车体横向加速度最大值

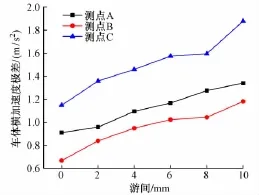
图10 不同工况下车体横向加速度极差

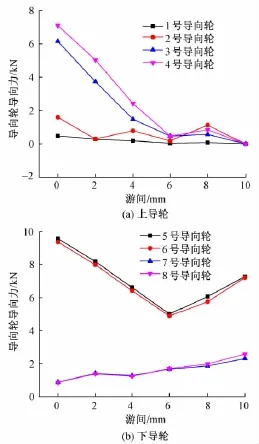
图11 不同工况下导向轮导向力最大值

从图8、图9可以看出，随着游间的逐渐增大，车体通过曲线时所受到的横向加速度也随之增大，当轮轨游间≥8 mm时，即轨距≥788 mm时，车厢两端，即前、后转向架中心对应的车厢底部，横向加速度值超过0.9 m/s2，即超过了车辆运行舒适度指标。而随着游间的增大，车体横向加速度的极差也随之增大，详见图10。

由图11中可以看出，随着游间的增大，转向架上部导向轮所受的导向力随之减小(转向架下部导向轮导向力先随游间的增大而减小);当游间增加到6 mm时，导向轮导向力出现随着游间的增大而增大的趋势。当游间为0，2 mm时，转向架上部的3号和4号导向轮导向力较大，转向架下部的5号、6号导向轮导向力也比较大。证明车辆侧向通过时，转向架发生了一定的倾斜，原因在于游间不足以提供足够的空间供转向架调整，使得不同侧且不同高度的两对导向轮受到挤压。当游间≥4 mm时，上部导向轮所受导向力减小幅度较大，均低于3 kN，而转向架下部导向轮导向力依然较大，为5～7 kN。

充分考虑悬挂式单轨交通系统的特殊性以及制造、建设的误差，认为悬挂式单轨轨道曲线段的合理轨距应大于导向轮外侧距。依据动力学仿真结果，可以得出悬挂式单轨轨道曲线段的合理轮轨游间为4～8 mm，即轨距值为784～788 mm。

4 结论

本文运用多体动力学软件，建立了多自由度悬挂式单轨交通系统动力学模型，并设定直线段轨距780 mm后通过动力学仿真，分析悬挂式单轨列车的曲线通过能力，即车辆通过曲线时车体响应随轨距的变化规律。结果表明:

1)曲线通过时，悬挂式单轨车辆横向加速度最大值随着轨距的增大而增大。车厢端部的横向加速度明显大于中部。当轨距≥788 mm时，车厢端部横向加速度超过舒适度标准。

2)曲线通过时，转向架将发生一定程度的偏转，导向轮导向力随轨距的增大先减小后增大，当轨距为784～788 mm，导向轮导向力最小。

3)充分考虑到制造安装误差以及后续轨道不平顺的发展，结合动力学仿真结果，最终确定悬挂式单轨曲线段合理轮轨游间为4～8 mm，即轨距为784～788 mm。

［1］RAHIER H W，SCHARF P．Sicherheits Technische Prufung Der Fahrerlosen Kabinenbahn Des Flugha—fens Duesseldorf［J］．Signal und Draht，2002，94(10):20-22．

［2］李芾，许文超，安琪．悬挂式单轨车的发展及其现状［J］．机车电传动，2014(2):16-20，76．

［3］许文超．悬挂式单轨车动力学性能研究［D］．成都:西南交通大学，2014．

［4］鲍玉龙．悬挂式单轨交通系统车桥耦合振动仿真研究［D］．成都:西南交通大学，2015．

［5］胡晓玲．悬挂式单轨车辆曲线通过性能研究［D］．成都:西南交通大学，2013．

［6］李忠继，林红松，颜华，等．空轨列车系统横向运动稳定性研究［J］．铁道科学与工程学报，2016(3):564-569．

［7］李成辉．轨道［M］．成都:西南交通大学出版社，2005．

［8］靳晓波．重庆跨座式单轨车辆关节道岔通过性能研究［D］．北京:北京交通大学，2007．

Research on Appropriate Track Gauge at Curved Section of
Suspended Monorail Transit System

HU Yibin1，Xiao Jieling1，Lin Hongsong2，WANG Ping1
(1．Key Laboratory of High-speed Railway Engineering，Ministry of Education，Southwest Jiaotong University，Chengdu Sichuan 610031，China;2．China Railway Eryuan Engineering Group Co．，Ltd．，Chengdu Sichuan 610031，China)

T he dynamic model of suspended monorail train system with multiple degrees of freedom was built according to multi-body dynamics theory，the vehicle dynamic responses were calculated by numerical integration，and the curving carrying capacity of suspended monorail train，which is the train body acceleration and the guiding force of the guiding wheel when the vehicle passes through the curves，was studied with different track gauges．T he results show that the lateral acceleration of suspended monorail train increases with the increasing of the track gauge when the train passes through curves，the lateral acceleration of train exceeds the comfort value which is 0.9 m/s2when the wheel-rail clearance is greater than 8 mm or the track gauge is greater than 788 mm，the guiding force of the guiding wheel firstly decreases and then increases with the track gauge increasing．According to the influence of track gauge on train body responses and guiding force of the guiding wheel，the recommended appropriate track gauge of suspended monorail transit system is 784～788 mm through considering the practical situation of engineering．

Suspended monorail transit;M ulti-body dynamics;W heel-rail clearance;T rack gauge

U213．2+15

A

10．3969/j．issn．1003-1995．2016．12．23

1003-1995(2016)12-0086-04

(责任审编孟庆伶)

2016-06-05;

2016-09-20

胡燚斌(1992—)，男，硕士研究生。