信息相关系数在列联表中的应用

2017-01-09刘成友张蓓蓓

中国卫生统计 2016年5期

丁勇刘成友张蓓蓓

信息相关系数在列联表中的应用

丁勇1△刘成友2张蓓蓓1

χ2检验在R×C列联表资料的统计研究中有着广泛的应用，但也存在着因样本量改变而使χ2值被过低或过高估计的问题，通过引进R×C列联表的关联系数，可在一定程度上克服这一缺陷［1－3］。关联度的分析是分析系统中各因素关联程度的方法，正确计算列联表资料的关联系数，不仅对于统计方法本身，而且对于实际应用都意义重大。目前常用的关联系数为Pearson列联系数［4－6］。本文将以信息论为基础的信息相关系数［7］应用于R×C列联表，并与Pearson列联系数进行比较，通过理论分析、实例计算和计算机模拟，我们发现信息相关系数更合适作为列联表关联系数的指标。

χ2检验的不足之处

一般的R行C列的R×C列联表数据如表1所示。χ2检验的统计量公式为［4－5］：

自由度v＝（R－1）（C－1）

由χ2值可求出相应的概率值

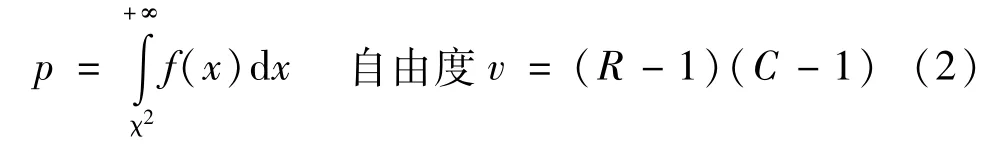
式中的f（x）为χ2分布的概率密度函数。实际应用中，p值一般通过查表或用各种数学、统计软件得到，为得到更精确的值，本文用数学软件Matlab的chi2cdf函数计算。

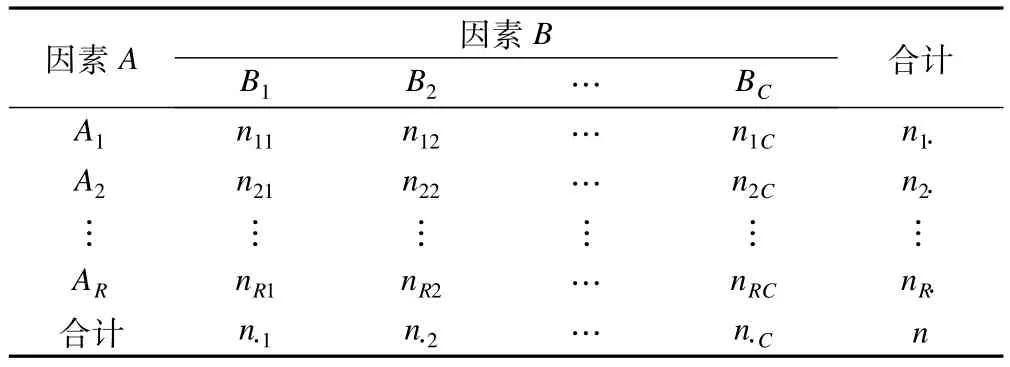
表1 R×C列联表数据

关于χ2检验的应用，先看一个简单的4格表例子。

例：某研究欲比较两种药物对治疗某疾病的效果，将325名治疗者随机分成2组，结果如表2所示，问两种药物的有效率是否相等？（显著性水平α＝0.05）

表2 两种药物治疗某种疾病的有效率

建立原假设H0：两种药物的有效率相同。

备择假设H1：两种药物的有效率不同。

把表1的所有数据扩大一倍，从而样本量也扩大1倍（n＝650），有效率保持不变时，由公式（1）不难求出此时χ2＝4.3337，故拒绝原假设，接受备择假设，认为两种药物的有效率不同。

考虑一般的R×C表，当样本量扩大k倍，而表中数据的比例不变，记此时的χ2值为由公式（1）可得

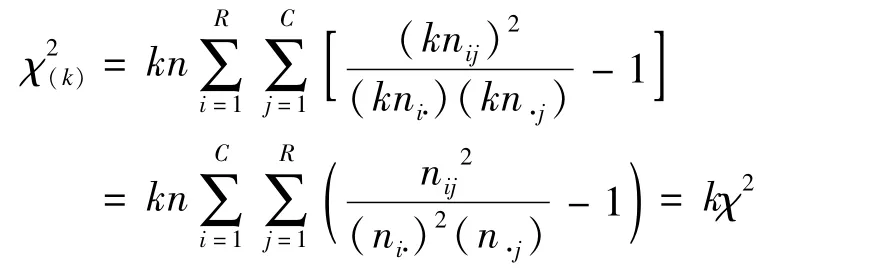
是原χ2值的k倍，但自由度仍然是v＝（R－1）（C－1）。因此，对给定的显著性水平α，如果原R×C表的但适当地扩大样本量倍数k，会有

仅仅由于样本量的变化，它们之间的比例关系没有发生变化，却导致了两个不同的结论，这说明χ2检验在应用中存在一定的不足之处。

列联系数和信息相关系数及其比较

为了解决χ2检验应用中的不足之处，引进不受样本量变化影响的关联系数。这些关联系数有［3］：Phi系数、Pearson列联系数、Cramer′s V等。目前最常用的关联系数是Pearson列联系数（以下简称列联系数），广泛出现在各种统计教材和实际应用中［3－6］。记列联系数为r，其计算公式为［4－5］

显然0≤r＜1。由公式（3）可知，当样本量扩大k倍时，r保持不变，因为

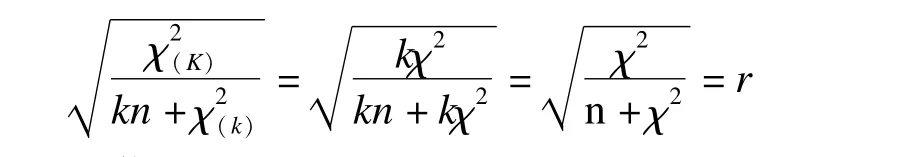
在信息论中，如果随机变量X的分布律为pi＝P（X＝xi）＞0（i＝1，2，…，m），则其信息熵定义为［8］其中b为对数的底，一般取b为2、e（自然对数）或10（常用对数）。文献［7］以信息熵为依据，提出了一种广义相关系数的概念，本文将其引入R×C列联表中，并称其为信息相关系数，定义如下：

把表1的因素A看成一个随机变量，有R个不同的状态Ai（i＝1，2，…，R），其概率分布为所以因素A的信息熵为把表1的因素B看成另一个随机变量，有C个不同状态Bj（j＝1，2，…，C），其概率分布为所以因素B的信息熵为两个因素A和B的联合概率分布为所以联合信息熵信息相关系数记为ρ，定义为

由对数换底公式不难证明，无论对数的底b取何值，公式（4）的结果都是相同的。

对表2的数据，按公式（3）和（4）可分别求出r＝0.0814和ρ＝0.0029。

当数据成比例扩大k倍时，由H（A）、H（B）和H（AB）的计算公式可知，它们保持不变，故ρ也保持不变，这一性质与列联系数相同。

文献已证明［7，9］：0≤ρ≤1；且当因素A和因素B相互独立时，H（AB）＝H（A）＋H（B），所以ρ＝0；当因素A和因素B完全相关时，H（AB）＝H（A）＝H（B），所以ρ＝1。

在我们前期研究［9－10］的基础上，本文做进一步的工作，说明信息相关系数可应用于R×C列联表，并且比列联系数更能反映真实情况。下面对列联系数和信息相关系数进行比较。

1.动态变化比较

为简单明了，取3×3列联表数据T＝［tij］，以样本总数的3种3×3列联表数据为例进行说明。

（1）完全相关列联表

取T为完全相关的列联表按公式（1）～（4）可得p＝0、r＝0.8165和ρ＝1。

对完全相关的列联表，显然信息相关系数等于1更符合实际情况，所以ρ要优于r。

再来看数据变动的情况：

T有9个元素，考虑给其中一个元素增加1个样本，其余元素不变，即样本总数为91时，分别考察r和ρ的变化情况。

上述计算表明，当增加的样本在对角线上时，仍然是完全相关资料，结果不变；ρ都为1，而r都为0.8165，所以仍然有ρ要优于r。

当增加的样本在其他6个位置时，不再是完全相关资料，r和ρ都相应地减少。

再考察不增加样本，但T1的任意的两行（或列）合并的情况：当T1成为2×3（或3×2）列联表，不再是完全相关资料时，都有r和ρ相应地减少。这些变化说明虽然r与ρ的值都变小，但r由0.8165变小，ρ由1变小，后者更符合实际情况。因为当列联表由完全相关资料变为不完全相关资料时，列联表的关联系数应该由1变为小于1。

（2）不相关列联表

取T为不相关的列联表按公式（1）～（4）可得P＝1、r＝ρ＝0，都与不相关列联表的关联系数应该为0相符合。

仿前增加1个样本。当第1行的3个元素的其中一个增加一个样本时，都有r＝0.0334，ρ＝0.0005；当第2行的3个元素的其中一个增加一个样本时，都有r＝0.0215，ρ＝0.0002；当第3行的3个元素的其中一个增加一个样本时，都有r＝0.0153，ρ＝0.0001。

增加1个样本时，T2不再是不相关列联表，关联系数应增加，上述计算结果与实际情况相符，两个关联系数都增加；且三种情况r与ρ的大小变化规律对应相同：增加的1个样本在第1行时增加最多，第2行次之，第3行最少。

仿前，当T2的任意两行（或列）合并成为2×3（或3×2）列联表时，仍然是不相关列联表，都有r＝ρ＝0，与实际情况相符。

（3）一般列联表

取T为一般的列联表（每行每列、正对角线都有5、10和15，但排列顺序不同，对称），按公式（1）～（4）可得p＝0.0047、r＝0.3780和ρ＝0.0794。

仿前，当T3的任意的两行（或列）合并成为2×3（或3×2）列联表时，都有r＝0.2774和ρ＝0.0515，都相应减少。

2.模拟比较

从上述三个例子数据，我们看到r与ρ的大小变化规律对应相同，但r比ρ更符合实际情况。下面进一步考察一般的情况。由于样本总数n＝90的3×3列联表的所有可能性是个巨大的数字，无法一一计算，所以我们用模拟数据进行研究。

数据模拟过程：利用Matlab函数random（′discrete uniform′，20，3，3），每次产生［0，20］区间上离散型均匀分布的3行3列随机整数矩阵，作为3×3列联表。其依据是，由数理统计知识可知，［0，20］区间上的均匀分布的随机数的均值（数学期望）为10，3行3列9个数据的样本总和的均值为90。

按照公式（1）～（4）计算模拟数据3×3列联表的p、r和ρ值。共进行10000次模拟，由于10000数据量较大，无法清楚地画出散点图，我们将p值范围［0，1］等分为10个小区间，对r和ρ求平均值，用平均值作图。结果见表3和图1、图2。

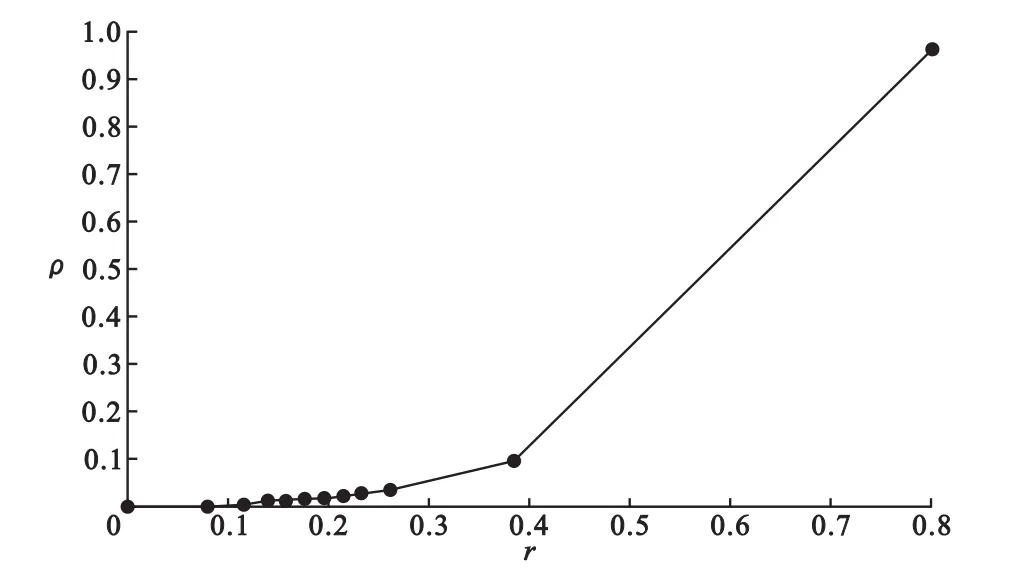
图1 r与ρ关系图

表3 小区间上列联系数平均值和信息相关系数平均值（10000次模拟结果）

用表3的数据，并结合完全相关列联表的p＝0、r＝0.8165和ρ＝1及不相关列联表的p＝1、r＝ρ＝0数据，可画出到r与ρ的关系图（图1）以及r和ρ与p（p取区间中点）的关系图（图2）。由图1可知，当r增大（或减小）时，ρ也增大（或减小），即对应的变化趋势是一致的，说明前面3个例子的分析结果具有普遍性。由图2可知，当p增大时，r和ρ都相应减小，p接近0时r＜ρ，p＞0.05时都有r＞ρ。

用同样的方法，我们又对样本总数为90的3×4、4×4、4×5和5×5的列联表情况进行了模拟，都得到了类似的结果。

讨论

列联系数r在实际问题中得到广泛应用，说明作为关联系数，它具有一定的合理性。以上比较表明，当样本量改变时，信息相关系数ρ与r的变化规律相同。此外，由公式（3）和（4）可知，这两个关联系数还有如下的共同特征：任意交换列联表的两行或两列，两个关联系数的值都不变。这些都表明，ρ与r有非常多的相同点和一致性，ρ同样也具有作为关联系数的合理性。

文献［6］认为，一个满意的相关度量应至少具备下列两个特点：（1）当两变量不相关时，其值应该等于0；（2）当两变量完全相关时，其值应该等于1。从上面列联表T1和T2的资料可知，列联系数r满足（1）但不满足（2），对完全相关的列联表T1，r仅为0.8165；由公式（3）也可知，对任意的R×C列联表都有r＜1。而信息相关系数ρ完全满足这两个特点，因而弥补了列联系数的这一缺陷。当两变量趋于完全相关时，p应趋于0，从而拒绝两变量不相关的零假设。图2表明，在p＝0附近，ρ值大于r值，接近于1。

我们认为，从实际应用出发，一个满意的相关度量还应具备如下特点：当p值较大，接收两变量不相关的零假设，也就是说，当认为两变量不相关时，关联系数值应较小。从不相关列联表T2的情况看，无论增加的一个样本在哪一行，都有较大的p（分别为0.9987、0.9998和0.9999），在实际应用中，都会接受两变量不相关的假设，所以这两个变量的关联系数都应较小，从上述计算来看，都有ρ＜r（0.0005＜0.0334，0.0002＜0.0215，0.0001＜0.0153）；从图2也可看出，对于较大的p，ρ＜r。因此，从实际应用来看，作为关联系数，ρ更合理。

由于R×C列联表为计数资料，而χ2分布是连续型分布，因此对于χ2值的精确计算，还存在不同的看法和争议［5，11－12］，有的认为要校正，有的认为不需校正。不同的计算，会得到不同的χ2值，由公式（3）可知，这时又会导致不同的列联系数。而信息相关系数是以信息熵为基础的，对变量的分布没有要求，与统计分布无关，既能描述变量间的线性相关关系，也能描述变量间的非线性相关关系，用公式（4）计算，不存在争议。许多研究资料（例如临床医学数据）由于其特殊性，变量之间关系复杂，很难确定变量的分布，因此，更适合用信息相关系数描述数据之间的相关性。

综上所述，我们认为，作为R×C列联表的关联系数，信息相关系数ρ比列联系数r更合适。本文抛砖引玉，希望在今后的各种实际问题中，应用这一指标，并进一步分析、比较，完善这方面的工作和研究，确定出一个更合理的关联系数指标。

［1］Roscino A，Pollice A．A Generalization of the Polychoric Corelation Coefficient．New York：Springer，2006：135-142．

［2］郑兵云．非参数检验的两个局限性问题．统计教育，2007，6：8-9．

［3］薛允莲，姜世强，刘贵浩等．列联表资料的关联强度．中国卫生统计，2011，28（3）：244-246．

［4］李贤平，沈崇圣，陈子毅．概率论与数理统计．上海：复旦大学出版社．2003．

［5］孙振球，徐勇勇主编．医学统计学．第4版．北京：人民卫生出版社，2014：102-107．

［6］李克均，时松和，胡东生．列联表的行列关联度与对应分析．中国卫生统计，2006，23（3）：261-263．

［7］丁晶，王文圣，赵永龙．以互信息为基础的广义相关系数．四川大学学报（工程科学版），2002，34（3）：1-5．

［8］王海燕．信息论基础．南京：东南大学出版社．2003：9-14．

［9］丁勇．平均互信息的可加性和广义相关系数不等式．工程数学学报，2007，24（2）：282-286．

［10］丁勇．离散型随机变量的平均信息熵．数学的实践与认识．202，42（18）：141-146．

［11］谭艺强．四格表资料三种检验方法分析．广东药学院学报，1999，15（1）：75-77．