新型大重合度齿廓齿轮时变啮合刚度研究

唐 沛, 刘亚成, 李慎龙, 李 晋

(中国北方车辆研究所 车辆传动重点实验室,北京 100072)

新型大重合度齿廓齿轮时变啮合刚度研究

唐 沛, 刘亚成, 李慎龙, 李 晋

(中国北方车辆研究所 车辆传动重点实验室,北京 100072)

针对内啮合齿轮传动的发展需求，提出了一种可广泛应用于内啮合齿轮的大重合度共轭齿廓，基于能量法计算了新型齿廓齿轮的弹性变形量，在此基础上，对新型大重合度齿廓齿轮进行有限元分析，并与能量法的计算结果进行对比，验证了能量法的有效性.建立了齿轮的法向刚度模型及齿轮副扭转刚度模型，研究结果对新型内啮合齿轮传动的齿廓设计具有借鉴意义，同时为新型内啮合齿轮传动的动力学分析提供了理论基础.

大重合度；新型齿廓；啮合刚度；能量法；有限元法

内啮合齿轮传动是齿轮传动的重要形式，与外啮合齿轮相比，具有效率高、重合度大、承载能力强等优点，被广泛应用于车辆、船舶等传动系统中.内啮合齿轮传动的齿形主要为渐开线和摆线，其中渐开线齿轮以其容易制造及互换性强，应用最为广泛，但渐开线齿轮在设计上受到齿形的限制，容易发生干涉，在设计中受最小齿数限制，有时还须进行变位加工以避免干涉，重合度也受齿数及压力角的限制.

随着新型传动结构的出现及对内啮合传动性能要求的提高，内啮合齿轮的设计应具有更高的承载能力和设计自由性.提高齿轮的承载能力通过两个方面实现：提高单齿强度或重合度，采用渐开线或摆线齿时，通过修形来提高齿轮的传动性能已经达到极限，同时，受到现有齿形的限制，在内啮合齿轮设计上，渐开线只能通过改变压力角和变为系数避免干涉，降低了内啮合齿轮设计的自由度.目前学者对外啮合齿轮设计进行了大量的研究，提出了许多新型齿形，但在内啮合齿轮设计方面，缺少相应研究.

文中以内啮合齿轮副为研究对象，基于齿轮啮合原理[1]和微分几何学[2]，提出一种新型大重合度内啮合齿轮齿形设计方法，建立了新型大重合度齿轮齿形的数学模型.在此基础上，基于能量法对新型齿廓齿轮的变形量进行研究，并结合有限元法进行验证，进而建立齿轮的法向刚度及扭转刚度模型.

1 大重合度内啮合齿轮齿形设计

提高啮合重合度是提升齿轮传动装置承载能力和传递效率、降低啮合冲击的有效途径，而接触迹线的长度是决定齿轮重合度的重要因素.下面以图1所示的内啮合渐开线直齿圆柱齿轮副的几何参数为基础，说明新型大重合度齿轮齿形的构造方法.

以两齿顶圆交点C为起点，节点B′为终点构造接触迹线，接触迹线可以为简单的圆弧，也可以为其他曲线，为了保证轮齿啮合，接触迹线限制在两齿顶圆之间.现在以过点C与点B′，圆心在AB上的圆弧B′C为接触迹线.以B′为坐标原点，建立固定坐标系S(xB′y),随齿条平动的坐标系S3(x3B′y3)，再分别以A、B为坐标原点，建立随齿轮1转动的坐标系S1(x1Ay1)及随齿轮2转动的坐标系S2(x2By2)，建立以B′点为坐标原点，初始位置时，4个坐标系的y轴重合.

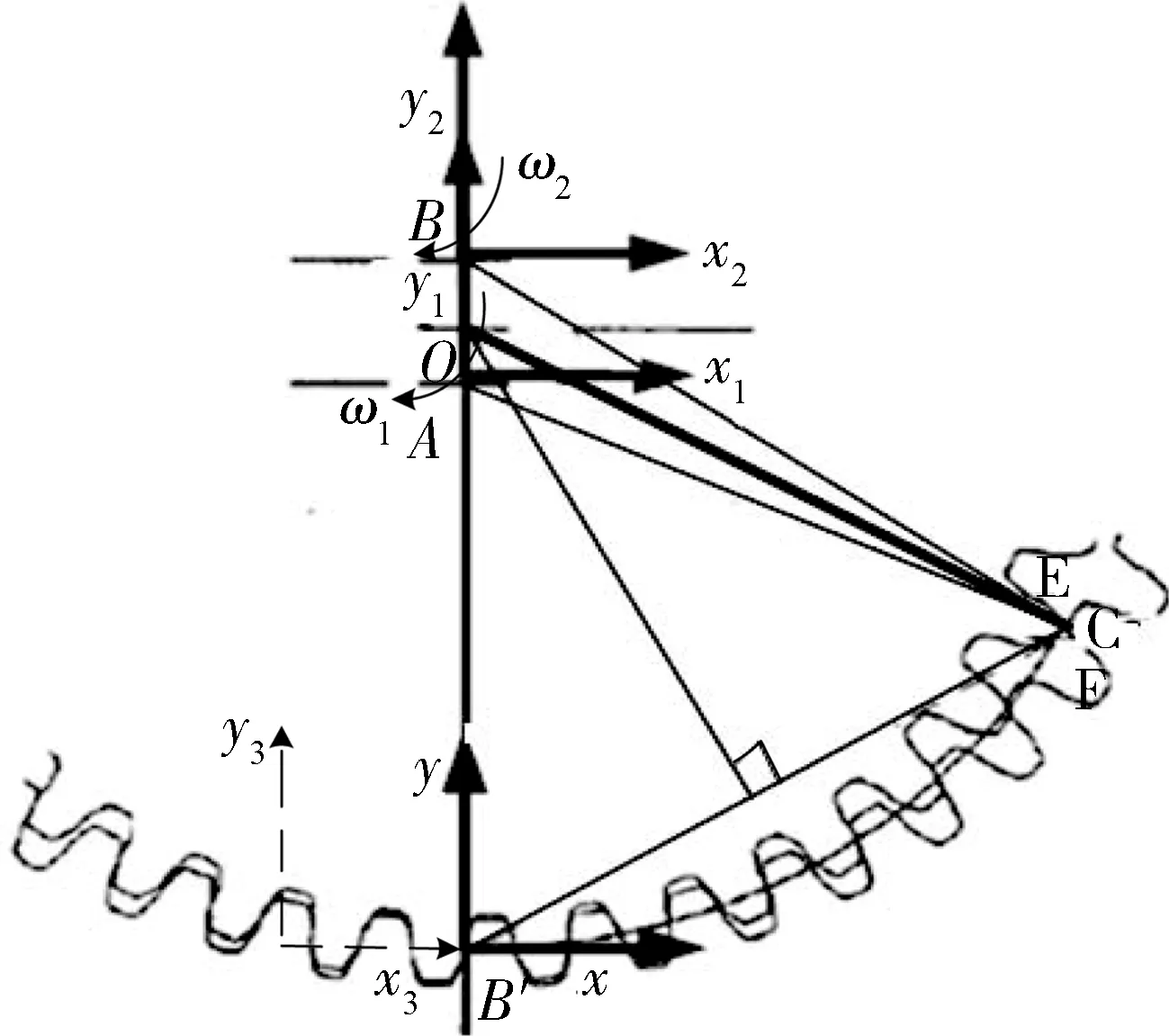
图1 啮合接触迹线几何关系

两齿轮齿顶圆交点C的坐标满足：

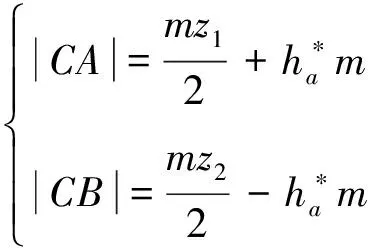
(1)

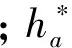
则点C(xc，yc)与啮合线中心O(x0，y0)在固定坐标系中坐标为

(2)

在固定坐标系下，啮合线的参数方程为

(3)

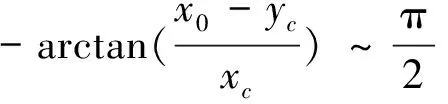
齿条齿廓满足：

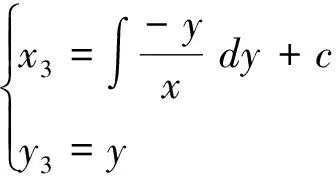
(4)

式中：c为积分常数，其值取决于齿廓与啮合线的交点位置.

(5)

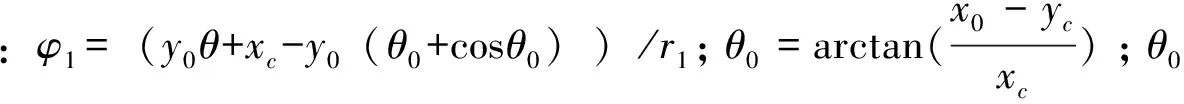
则外齿轮1参与啮合的齿廓方程为

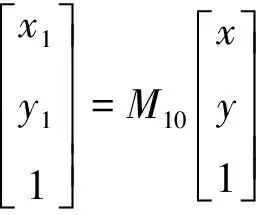
(6)

同样的方法求得与上述齿廓共轭的内齿轮2的齿廓方程为

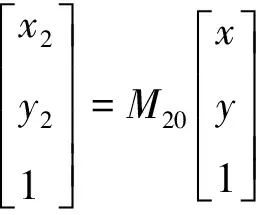
(7)

坐标变换矩阵

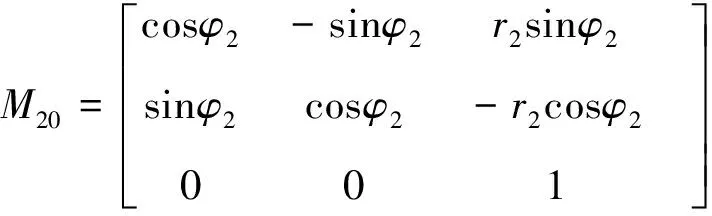
式中：φ2=(y0θ+xc-y0(θ0+cosθ0))/r2.

新齿形齿轮啮合过程中，节点以下齿廓不参与啮合，因此,该部分齿廓的设计原则为：在保证齿根齿廓不干涉的前提下，最大限度的提高轮齿弯曲强度.采用直接复制与之共轭齿轮的齿顶齿廓，并光滑过渡到齿根圆的方法得到节点以下齿廓.由于节点以下部分不参与啮合，所以设计出的新齿形齿轮不存在根切问题.研究表明设计出的新型大重合度齿廓齿轮主要具有如下特点：①最小重合度为π，选取合适的设计参数，重合度可达10以上，可大幅度提高齿轮传动装置的寿命；②滑移率较小，齿轮齿面磨损均匀；③加工时无根切现象，对齿轮传动装置的轻量化、小体积设计十分有利.新型大重合度内啮合齿轮齿形可广泛应用于内啮合齿轮传动，尤其对近年来提出的新型双内啮合行星齿轮传动装置[3-5]的研制具有重要意义，并已被用于该传动装置的样机中.

2 基于能量法的新型大重合度齿廓齿轮刚度计算

齿轮的时变啮合刚度是齿轮动力学动态响应中最重要的一项激励参数，也是齿轮系统产生振动和噪声的重要原因，对刚度激励进行研究具有重要意义[6].

因载荷作用齿轮变形存储的势能U由弯曲势能Ub、剪切势能Us、压缩势能Ua、接触势能Uh、齿基势能Uf组成，变形能与变形量之间满足卡式定理.基于能量原理[7]与卡式定理，可将轮齿视为图2所示的非均匀悬臂梁[8]，Le为有效长度，其值等于基点M至顶圆的距离.轮齿有效接触部分沿对称轴线被分成一系列长方形微元，每个微元由符号i表示.对每个长方形微元，它的高度、横截面积和对中性轴的惯性矩I被取为两个侧面的平均值.Fj是齿轮啮合点j传递的载荷，δj是单个轮齿在j点沿Fj方向的变形.弹性变形量δj主要有3部分构成：①轮齿部分的弯曲变形、剪切变形和轴向压缩变形；②与齿相连的过渡圆角处基体的变形;③由接触应力引起的局部接触变形.

2.1 轮齿部分变形计算

将受载轮齿简化为图2所示的悬臂梁模型，计算轮齿变形时，认为每个微元左端固定，且与微元相连接的右端面部分是刚体，沿作用力方向的变形δbj是单个微元变形δbij的叠加.与渐开线齿轮最显著不同的一点是，新型大重合度齿廓齿轮的啮合区为节点到齿顶的齿廓段，齿根到节点间齿廓不参与啮合.

图2 轮齿悬臂梁模型

X轴方向的分力Fx、Y轴方向的分力Fy、等效弯矩M满足：

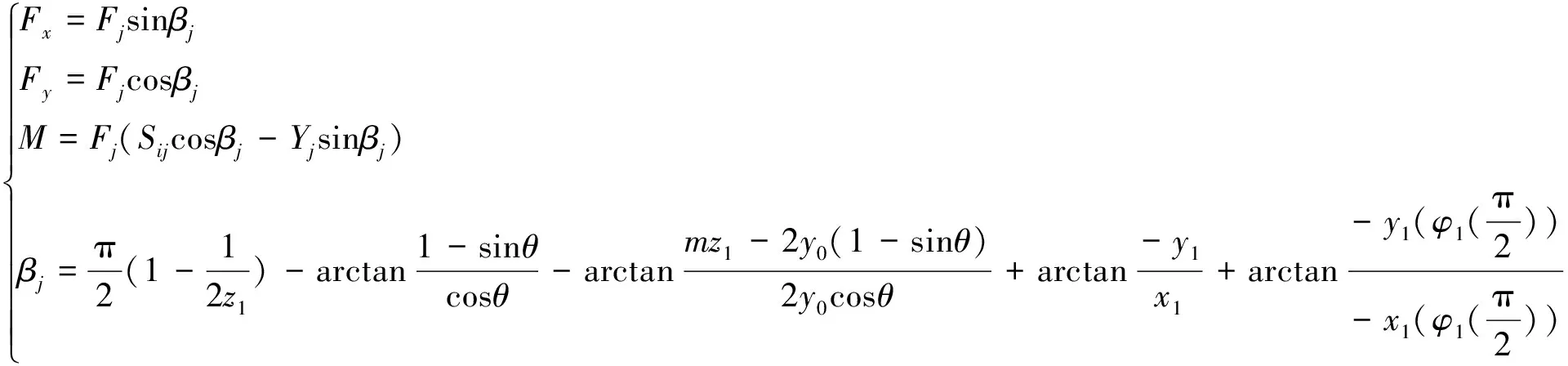
(8)

结合材料力学中的梁理论，可知：

(9)

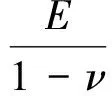
与渐开线齿廓不同的是新型齿轮的啮合区与非啮合区齿廓方程不统一，Ii、Sij、Ai需分段计算.

2.2 基体变形计算公式

根据Cornell[10]对齿轮基体变形量的推导，新型大重合度齿廓齿轮的基体变形量δfj满足相关要求，即平面应力状态下δfj满足公式：

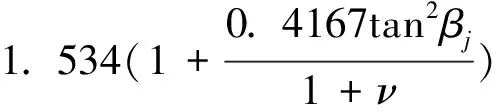
(10)

平面应变状态下δfj满足：

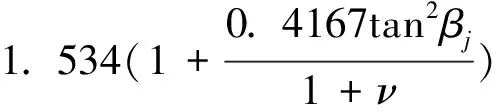
(11)

根据有效长度Le，可求出Lf和Hf为

Lf=Xj-XM-Yjtan(βj)，

Hf=2YM.

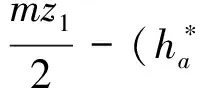
2.3 局部接触变形计算公式

Hertz接触理论[11]表明轮齿在未承载时，接触表面产生局部弹性变形，形成一个宽度为2b的矩形接触面，由齿轮啮合力、应力、应变、胡克定律之间的关系式：

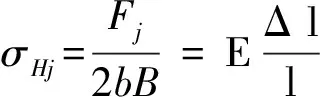
(12)

可知，齿轮的接触变形量

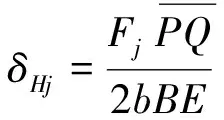
(13)

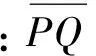
2.4 刚度计算

由齿轮变形量δj与齿轮法向刚度kj的关系式，可建立齿轮单齿法向刚度模型：

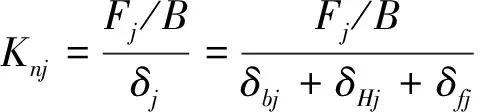
(14)

内齿轮的变形量可采用与外齿轮相同的计算方法确定，进而建立内齿轮的单齿刚度模型.由建立的内、外齿轮单齿刚度模型，可建立单对轮齿法向啮合综合刚度模型：

(15)

式中：Kn∑为单对轮齿啮合综合刚度;δ1j、δ2j分别为内、外齿轮啮合点沿啮合力方向的弹性变形量.

新型大重合度齿廓齿轮在同一啮合时刻，有多对齿参与啮合，不同啮合齿间法向刚度的方向不同,因此,在利用上述模型计算出来的单齿啮合刚度计算整个齿轮副多齿啮合刚度时，不能通过将单齿的法向刚度简单相加求得，需要利用扭转啮合刚度建立新型大重合度齿廓齿轮传动的综合刚度模型.齿轮副啮合刚度模型如下：

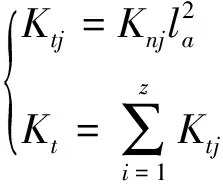
(16)

式中:Ktj为单对齿啮合的扭转刚度;la为接触线的力臂;Kt为齿轮副扭转刚度;z为同时参与啮合的齿轮对数.

3 实例分析

某型履带车辆变速器中的内啮合齿轮副几何参数如表1所示.

表1 齿轮基本参数

基于渐开线齿轮齿廓的几何参数，根据推导出的新型齿廓参数方程，构造大重合度内啮合齿轮齿形，其齿形方程为

,(17)

式中：φ1=(61.061 2θ-31.718 6)/55.5；φ2=(61.061 2θ-31.718 6)/67.5；θ在29.762 6°～90°间.图3为该新型大重合度齿廓内啮合传动的三维模型.

图3 新型大重合度齿形齿轮传动

下面采用有限元法对建立的刚度模型进行验证.由于齿宽大于齿厚，满足平面应变假设，可利用齿轮的二维模型进行分析，有限元模型如图4所示，完全约束齿轮内孔，在啮合点处建立局部坐标系，局部坐标系的X轴沿啮合力的作用线方向，在齿廓表面的不同啮合位置施加不同方向的单位啮合力来模拟齿轮的啮合，提取两个齿轮的变形量，表2为15个不同啮合位置的变形量.

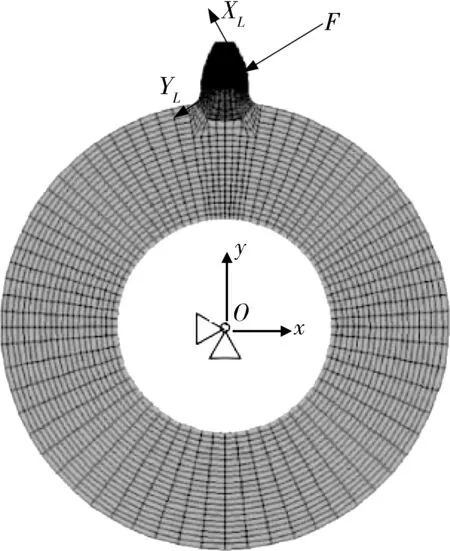
图4 外齿轮变形量分析有限元模型

表2 齿轮不同啮合点变形量

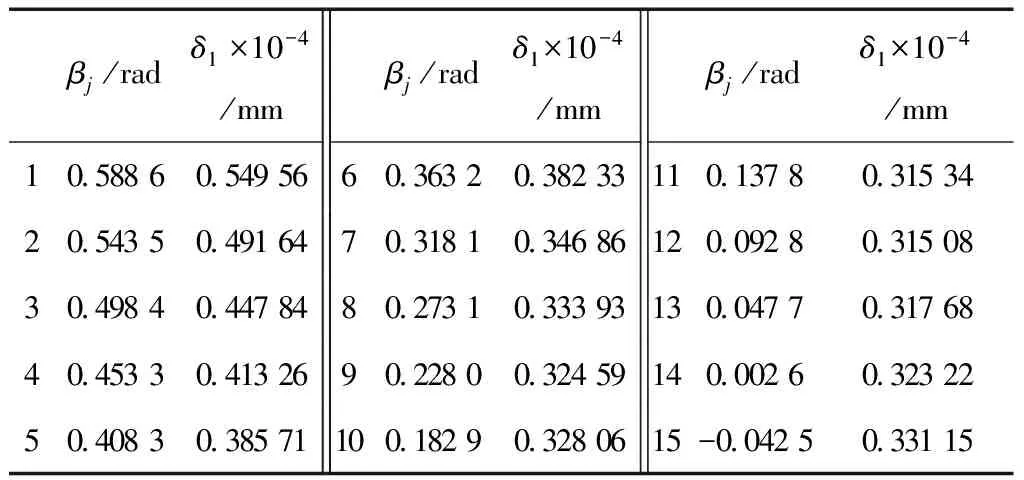
βj/radδ1×10-4/mmβj/radδ1×10-4/mmβj/radδ1×10-4/mm1058860549566036320382331101378031534205435049164703181034686120092803150830498404478480273103339313004770317684045330413269022800324591400026032322504083038571100182903280615-00425033115

基于能量法建立的啮合点变形模型，编制MATLAB程序，计算与表2中相同的15个啮合位置的变形量，图5为两种方法计算结果的对比：

图5 有限元法与能量法外齿轮变形量计算对比

可见，基于能量法的变形量计算具有较高的准确性，由能量法计算的变形量推导出的刚度模型也就具有工程应用价值.图6为基于能量法建立的内、外齿轮相应的法向刚度与扭转刚度模型.

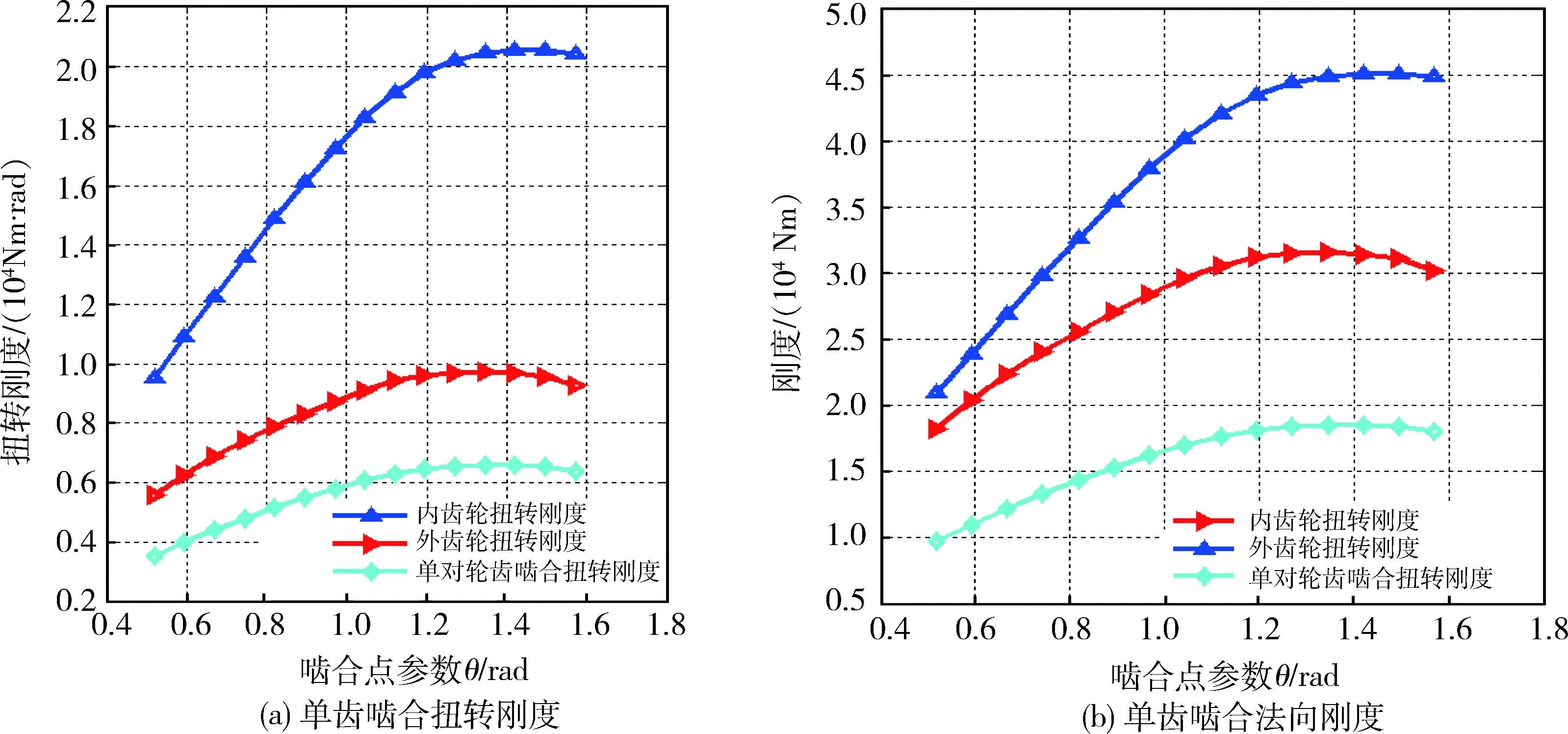
图6 单对轮齿啮合刚度

基于已建立的单对轮齿的扭转刚度模型，并考虑齿轮啮合过程中，啮合齿轮对数的动态变化，以在齿顶处刚进入啮合的外齿轮的轮齿为参照，可建立齿轮副的扭转刚度模型，如图7所示.

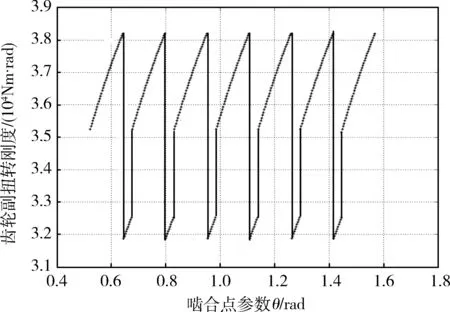
图7 齿轮副扭转刚度

外齿轮的参照齿从啮入至啮出的过程中，啮合齿对数在7与6间交替变化，导致齿轮副扭转刚度如图7动态变化.

4 结 论

提出了一种大重合度齿轮齿形构造方法，这种大重合度齿形可应用于高速重载内啮合齿轮传动，对新型双内啮合行星齿轮传动装置的研制具有使用价值.将轮齿视为齿根圆上的悬臂梁，基于弹性力学中的能量原理，求解轮齿的变形量，进而建立了齿轮的法向刚度模型.有限元分析结果验证了能量法求解新型大重合度齿形轮齿变形量的正确性及有效性.最终建立了齿轮的法向刚度模型、扭转刚度模型及齿轮副的扭转刚度模型，为这类新型齿轮传动的啮合动力学分析提供相应的理论基础.

[1] 李特文.齿轮啮合理论[M].上海:上海科技出版社,1984.

[2] 梅向明,黄敬之.微分几何 [M]. 2版,北京:高等教育出版社,1988.

[3] John H.Kerr.Incrementally Variable Transmission: Canada, 4559848[P].1985-12-24.

[4] John H.Kerr.Coplanar Reverted Gear Train Loop: Canada, 6126566[P].2000-10-03.

[5] 李慎龙,周广明,赵 凯,等.高效双模逻辑机械综合传动技术研究[J].车辆与动力技术.2014(3):1-3.

[6] 李润方,齿轮系统动力学—振动、冲击、噪声[M].北京:科学出版社,1997.

[7] 付宝连.弹性力学中的能量原理及其应用[M].北京:科学出版社,2004.

[8] 颜海燕,唐进元,宋红光.直齿轮轮齿变形计算的数值积分法[J].机械传动,2005,29(2):7-9.

[9] 杨长辉,徐涛金,许洪斌,等.基于Weber能量法的直齿轮时变啮合刚度数值计算[J].机械传动,2015,39(2):59-62.

[10]Cornell R W.Compliance and stress sensitivity of Spur Gear Teeth[J].Journal of Mechanical Design,1981,103(2):447-459.

[11]罗继伟,罗天宇.滚动轴承分析计算与应用[M].北京:机械工业出版社,2009.

Study on Time-Varying Mesh Stiffness of a Novel Tooth ProfileGear with Great Contact Ratio

TANG Pei, LIU Ya-cheng, LI Shen-long, LI Jin

(Science and Technology on Vehicle Transmission Laboratory, China North Vehicle Research Institute, Beijing 100072, China )

According to the development requirement of the internal meshing gear transmission, a new type of the conjugate tooth profile is proposed with a great contact ratio. Based on the energy method, the elastic deformation of the new profile is calculated at their contact points, and the finite element analysis of the gear is carried out. The simulated outcomes are compared with the former calculating results, verifying the validity of the energy method. Both a normal stiffness model of the gear and a torsional stiffness model of its gear-pair are established. The studied results have reference value for the design of the new internal gear transmission, and provide a theoretical basis for the dynamics analysis of the novel transmission.

great contact ratio; novel tooth profile; mesh stiffness; energy method; finite element method

1009-4687(2016)04-0003-06

2016-9-6

国家探索研究项目(7131458)

唐 沛(1989-)，男，研究方向为行星传动技术.

TJ811

A